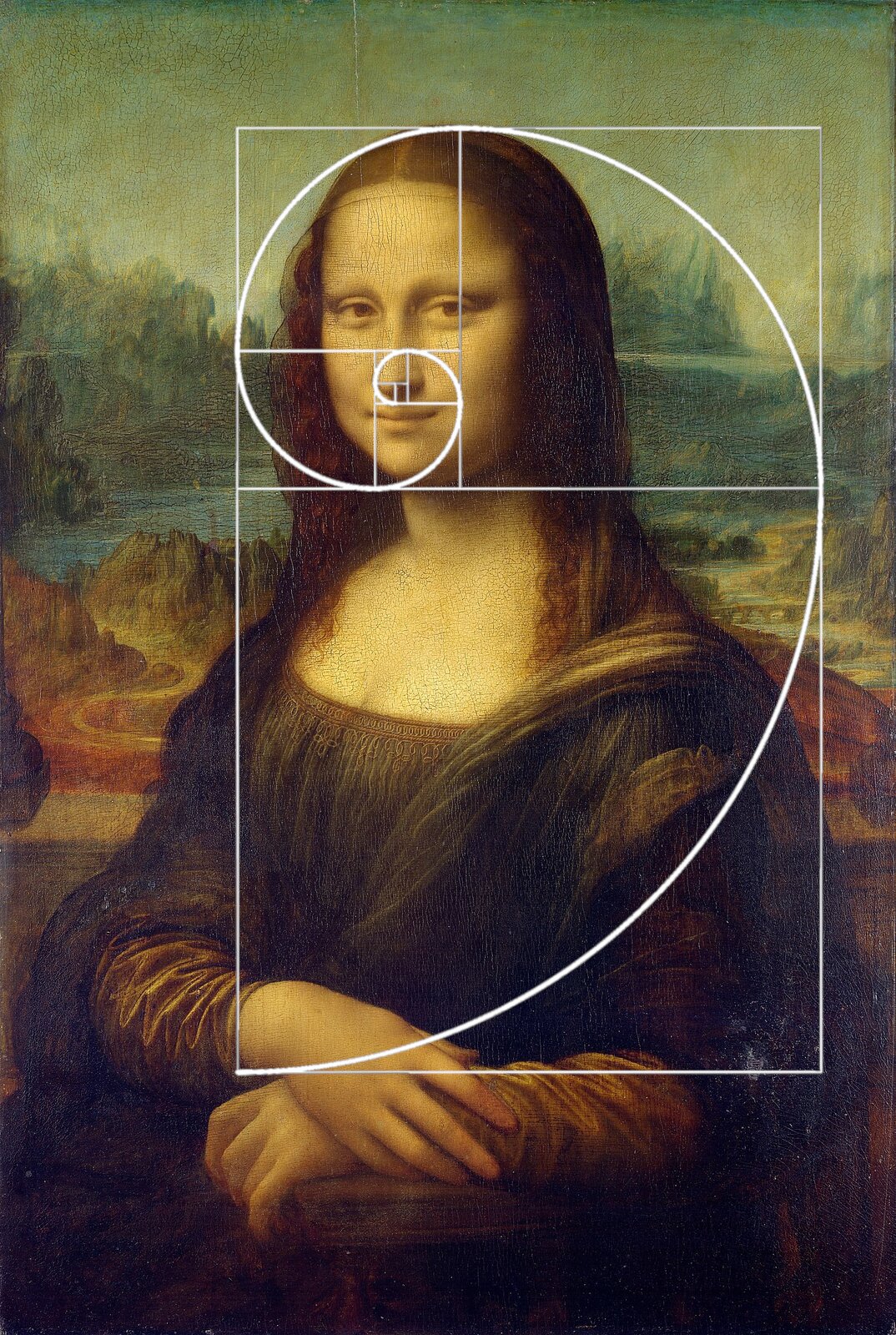Ciąg Fibonacciego, historia o królikach
Co wspólnego mają ze sobą włoski matematyk i króliki? Na pierwszy rzut oka pewnie niewiele, jednak to właśnie rozwiązując problem polegający na wzroście populacji królików, Fibonacci opisał słynny ciągciąg. Seria tych liczb jest tak wyjątkowa, ponieważ możemy ją znaleźć niemalże wszędzie – w przyrodzie, anatomii, fizyce czy zjawiskach przyrodniczych. Artyści czy architekci w swoich pracach często czerpią inspirację właśnie z ciągu Fibonacciego.
W tym materiale poznamy bliżej ten ciąg i jego zastosowanie.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
MultimediumMultimedium
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
BibliografiaBibliografia
Wyjaśnisz, czym jest ciąg liczbowy.
Wyznaczysz kolejne wyrazy ciągu Fibonacciego.
Scharakteryzujesz własności ciągu Fibonacciego.
Zapoznasz się ze złotym prostokątem oraz spiralą Fibonacciego.
Leonardo Fibonacci

Fibonacci, znany również jako Leonardo Fibonacci, Filius Bonacci czy Leonardo Pisano, to włoski matematyk. Żył w latach 1175–1250. Fibonacci kształcił się w Afryce Północnej, najpierw pod nadzorem arabskiego nauczyciela, a następnie do 25 roku życia uczył się samodzielnie, jednocześnie podróżując po różnych krajach, dzięki czemu poznał dorobek wielu matematyków.
Ciąg Fibonacciego – historia o królikach
Fibonacci w swojej książce Liber abaci sformułował problem: Pewien mężczyzna ma parę królików w zamkniętym pomieszczeniu. Chce on się dowiedzieć, ile par królików będzie miał za rok, jeśli króliki będą się rozmnażać i każda para będzie płodzić kolejne nowe pary królików. Dodatkowo zapisał też następujące zasady:
króliki nie chorują, nie starzeją się ani nie umierają, więc ich liczba nie maleje;
nowo narodzona para królików może mieć potomstwo dopiero po miesiącu od urodzenia;
każda para królików, która jest wystarczająco dorosła, a więc ma przynajmniej miesiąc, wydaje na świat kolejną parę królików.
Na początku mężczyzna miał jedną parę królików. Były młode i niezdolne do rozmnażania się, a więc po miesiącu mężczyzna nadal miał tylko jedną parę królików.
Po pierwszym miesiącu para ta zdolna była już do rozmnażania się, dzięki czemu w trzecim miesiącu urodziła się nowa para królików, a więc mężczyzna miał już dwie pary.
W kolejnym miesiącu młode króliki nie mogły się jeszcze rozmnażać, więc tylko jedna para była zdolna do wydania młodych.
W czwartym miesiącu urodziła się nowa para królików. Mężczyzna miał więc już trzy pary królików, z czego dwie mogły się rozmnażać.
W piątym miesiącu urodzą się zatem dwie pary królików, a trzy zdolne będą do rozmnażania się – w sumie pięć par.
W miesiącu szóstym urodzą się trzy pary królików, a pięć par będzie zdolnych do rozmnażania – w sumie osiem par.
W miesiącu siódmym urodzi się pięć par królików, a osiem zdolnych będzie do rozmnażania się – w sumie trzynaście par.
W miesiącu ósmym urodzi się osiem par królików, a trzynaście par zdolnych będzie do rozmnażania się – w sumie dwadzieścia jeden par.
W miesiącu dziewiątym urodzi się trzynaście par królików, a dwadzieścia jeden par zdolnych będzie do rozmnażania się – w sumie trzydzieści cztery pary.
W miesiącu dziesiątym urodzi się dwadzieścia jeden par królików, a trzydzieści cztery pary zdolne będą do rozmnażania się – w sumie pięćdziesiąt pięć par.
W miesiącu jedenastym urodzą się trzydzieści cztery pary królików, a pięćdziesiąt pięć par zdolnych będzie do rozmnażania się – w sumie osiemdziesiąt dziewięć par.
W miesiącu dwunastym, a więc po roku, urodzi się pięćdziesiąt pięć par królików, a osiemdziesiąt dziewięć par zdolnych będzie do rozmnażania się – w sumie sto czterdzieści cztery pary.
Czytając taki opis, trudno zauważyć zależności między kolejnymi miesiącami a liczbą par królików. Przedstawmy więc je na schemacie. Z racji dużej liczby par, na schemacie ograniczymy się do sześciu miesięcy.
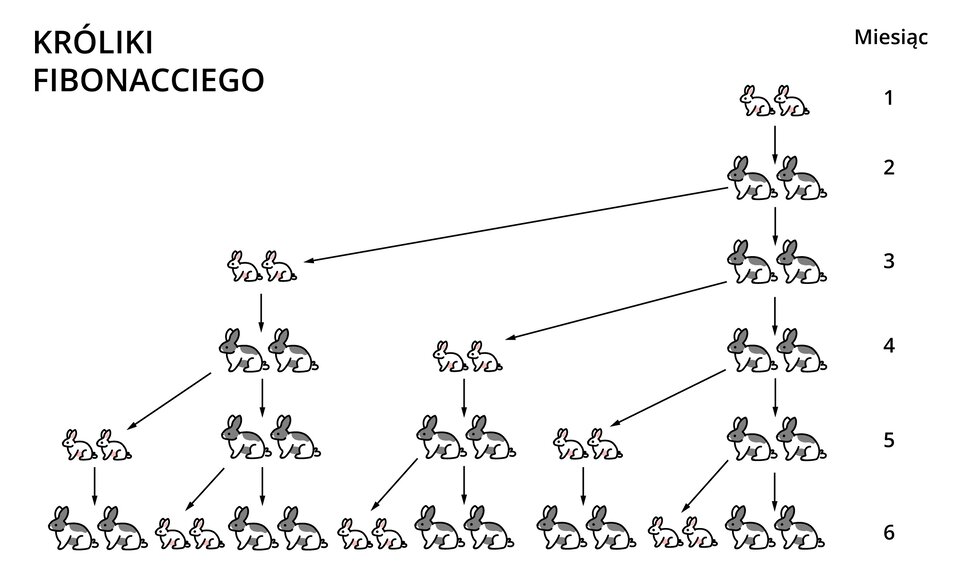
Niech aIndeks dolny 11 oznacza liczbę par królików w pierwszym miesiącu, aIndeks dolny 22 liczbę par w drugim miesiącu oraz aIndeks dolny nn liczbę par w n‑tym miesiącu (tzn. gdy n = 3, to jest to liczba par w trzecim miesiącu, a gdy n = 4, to w czwartym itd.).
Dzięki tak przedstawionym informacjom możemy zapisać następujące zależności:
Oznacza to, że dwie pierwsze liczby (które w ciągu nazywamy wyrazami) ciągu Fibonacciego równe będą 1, a każdy następny wyraz będzie sumą dwóch poprzednich wyrazów. Obliczając kolejne wyrazy ciągu Fibonacciego na kartce papieru, możemy to zrobić w prosty sposób, tak jak przedstawiono to na ilustracji poniżej:
Wyraz | Kolejne wyrazy ciągu |
|---|---|
1 | 1 |
2 | 1 |
3 | 1 + 1 = 2 |
4 | 1 + 2 = 3 |
5 | 2 + 3 = 5 |
6 | 3 + 5 = 8 |
7 | 5 + 8 = 13 |
8 | 8 + 13 = 21 |
9 | 13 + 21 = 34 |
10 | 21 + 34 = 55 |
11 | 34 + 55 = 89 |
12 | 55 + 89 = 144 |
13 | 89 + 144 = 233 |
14 | 144 + 233 = 377 |
15 | 233 + 377 = 610 |
16 | 377 + 610 = 987 |

Zaliczanie zera do elementów ciągu Fibonacciego zależy od umowy i konwencji przyjętej przez autora. W niektórych definicjach pierwszym wyrazem ciągu jest 0, a w innych 1. Obie definicje są poprawne, a ich użycie zależy od kontekstu, np. w przypadku problemu rozmnażania się królików, bardziej naturalne wydaje się rozpoczęcie ciągu od 1. Z matematycznego punktu widzenia, aIndeks dolny 00 może przyjmować 0 jako pierwszy wyraz, wówczas:
Kolejne wyrazy ciągu pozostają niezmienne, jedyna różnica to 0 na samym początku.
Złota liczba
Potrafimy już obliczyć kolejne wyrazy ciągu, ale co z tego wynika? Okazuje się, że gdy weźmiemy pod uwagę dwa kolejne wyrazy ciągu i podzielimy wyraz większy przez wyraz mniejszy, otrzymamy przybliżenie tak zwanej złotej liczby. Dla przykładu, dzieląc wyraz szesnasty przez wyraz piętnasty, otrzymamy:
Dzieląc wyraz ósmy przez wyraz siódmy, otrzymamy:
Jeżeli obliczymy kolejne ilorazy coraz większych wyrazów ciągu, otrzymamy dokładniejsze przybliżenie złotej liczby. Liczbę tę oznaczamy grecką literą ⲫ.
Ciąg Fibonacciego oraz złotą liczbę spotkać możemy np. w przyrodzie, jednak nie w sposób bezpośredni. Na kwiatku nie znajdziemy cyfr, nie usłyszymy ich też w śpiewie ptaków. Dookoła nas możemy jednak dostrzec złotą spiralę, która związana jest z ciągiem Fibonacciego.
Oto kilka przykładów spirali Fibonacciego w naturze:
Jeśli chcesz zobaczyć, w jaki sposób jest tworzona złota spirala, przejdź do symulacji interaktywnej znajdującej się w dalszej części e‑materiału.
Rysując obok siebie kwadraty o długościach boków opowiadających kolejnym wyrazom ciągu Fibonacciego, otrzymamy złoty prostokąt.
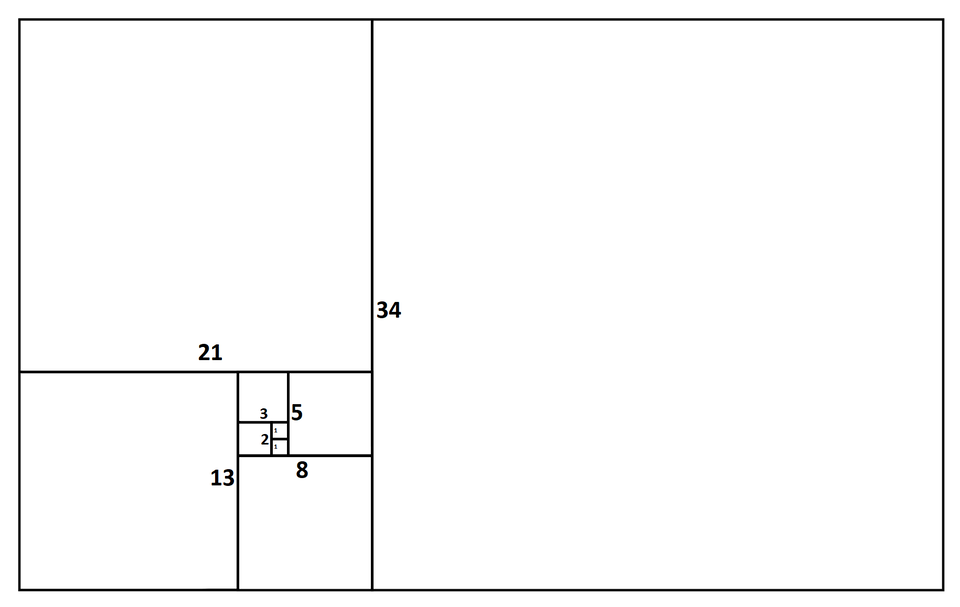
Następnie, łącząc ćwiartkami okręgów dwa wierzchołki każdego kwadratu, otrzymamy spiralę. Taką spiralę nazywamy spiralą Fibonacciego i jest ona przybliżeniem tzw. złotej spirali, w której co 90 stopni szerokość zwiększa się phi razy.

Złoty prostokąt, chociaż nie w tak oczywisty sposób jak w naturze, jest również obecny w sztuce czy architekturze:
Notatnik
Gra edukacyjna
Symulacja interaktywna
Korzystając z symulacji, wyświetl spiralę Fibonacciego. Na kartce narysuj spiralę dla pierwszych ośmiu elementów ciągu Fibonacciego.
Zestaw ćwiczeń interaktywnych
Zapoznaj się z ilustracją i wykonaj ćwiczenie.
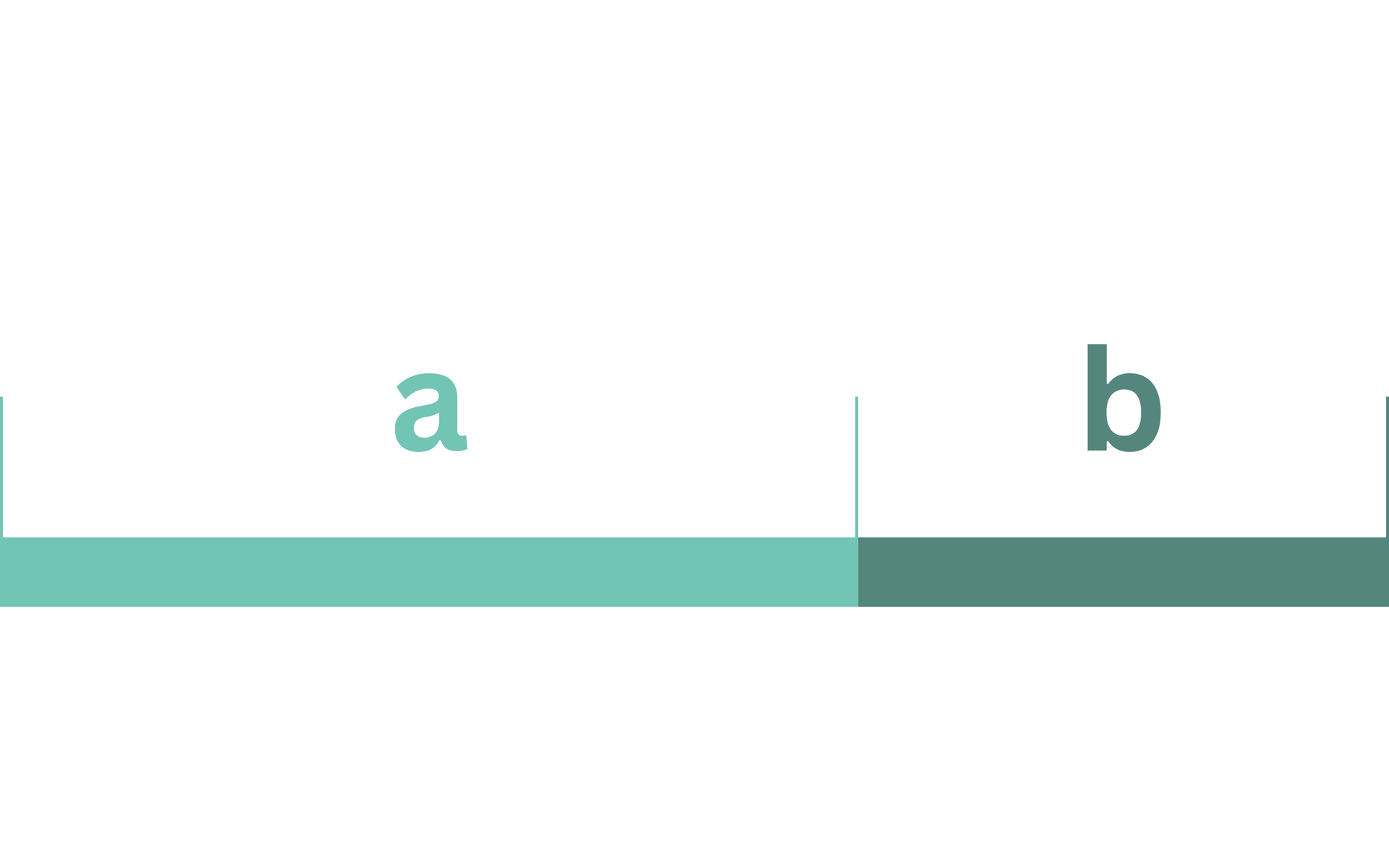
Przyrost liczby gałęzi pewnego drzewa w okresie kolejnych miesięcy zwiększa się w określony sposób. Liczba gałęzi w kolejnych miesiącach odpowiada danemu wyrazowi ciągu Fibonacciego. W pierwszym i drugim miesiącu liczba gałęzi wynosi 1. W trzecim miesiącu wynosi 2. W czwartym miesiącu wynosi 3 itd.
Przedstawiamy to na ilustracji.

Słownik
funkcja określona w zbiorze liczb całkowitych dodatnich; wartości tej funkcji dla kolejnych liczb naturalnych nazywamy wyrazami ciągu
podział odcinka na dwie części tak, aby stosunek dłuższej z tych części do krótszej był taki sam, jak stosunek długości całego odcinka do długości dłuższej części.
Bibliografia
Cybulska J., Ciąg Fibonacciego, zpe.gov.pl/b/ciag‑fibonacciego/PEwsOysjE, dostęp 08.03.2024.
Lenda A., Liczby Fibonacciego, ftj.agh.edu.pl/~lenda/cicer/fibo.htm, dostęp 08.03.2024.
Sikora K., Dlaczego tak trudno znaleźć czterolistną koniczynę?, nauka.uj.edu.pl, dostęp 08.03.2024.