Własności figur geometrycznych na płaszczyźnie
1. Figury płaskie
Słowo geometria pochodzi z języka greckiego i oznacza „mierzenie ziemi” (geo to ziemia, metroin to mierzyć). W starożytnej Grecji, a wcześniej jeszcze w Egipcie, geometrzy pełnili taką rolę, jaką dziś pełnią geodeci. Wykonywali pomiary działek – wyznaczali granice, obliczali pola powierzchni. Używali przy tym sznurów i prostych przyrządów, które przypominały cyrkle. Działki egipskich chłopów były corocznie zalewane przez Nil, zatem geometrzy ciągle doskonalili swoje umiejętności, aby terminowo wykonać pilne prace.
Rozglądając się dokoła, zauważamy rozmaite obiekty trójwymiarowe. Opisując je, możemy określić ich długość, szerokość, wysokość lub głębokość. Takie obiekty to figury przestrzenne (bryły). Badaniem własności brył zajmuje się stereometria (z języka greckiego stereo to przestrzeń).
Cienie brył (w geometrii zwane rzutami) mają kształt figur płaskich. Badaniem własności figur płaskich zajmuje się nauka zwana planimetrią (z języka greckiego plano to płaszczyzna, metroin to mierzyć).

Film dostępny pod adresem /preview/resource/R1dOTeq3pCKJm
Animacja przedstawia skąd wywodzi się nazwa geometria i do czego ona służyła w starożytności.
Jakie figury płaskie można dostrzec na rysunkach?

Na liście nazwisk zapisanych na wieży Eiffla znajduje się nazwisko francuskiego matematyka, fizyka i chemika Gasparda Monge’a, żyjącego na przełomie i w.
Monge opracował metodę odwzorowywania brył na prostopadłe względem siebie płaszczyzny. Metoda ta, zwana rzutami Monge, jest stosowana powszechnie do rozwiązywania wielu problemów geometrycznych.
Zastanów się, jak zmienia się cień obracającego się sześcianu.
Jak myślisz – jaką figurę płaską będzie przypominał cień sześcianu, na który popatrzymy z góry? A z boku?
Czy można tak umieścić sześcian, by patrząc z góry, widzieć sześciokąt?
Jakie inne figury płaskie przypominają ci cienie sześcianu?
Sprawdź swoje przypuszczenia.

Film dostępny pod adresem /preview/resource/RHr5bZmlFDexk
Animacja 3D pokazuje obracający się sześcian, który pozostawia na płaszczyźnie różne odbicia.
Punkt, prosta, wzajemne położenie prostych
Najprostszą figurą geometryczną jest punkt.
Wszystkie pozostałe figury geometryczne składają się z punktów.
Punkty oznaczamy dużymi literami.
Modelem punktu może być kropka narysowana ołówkiem, gwiazda zaobserwowana na niebie lub na przykład zmniejszający się obraz Księżyca widzianego ze statku kosmicznego.

Film dostępny pod adresem /preview/resource/R1B72EQWtXwRf
Animacja przedstawia, że obserwowane przez nas gwiazdy przypominają punkty.
Przykładem figury, która składa się z nieskończenie wielu punktów, jest prosta.
Proste oznaczamy małymi literami, na przykład: , , , , , , .

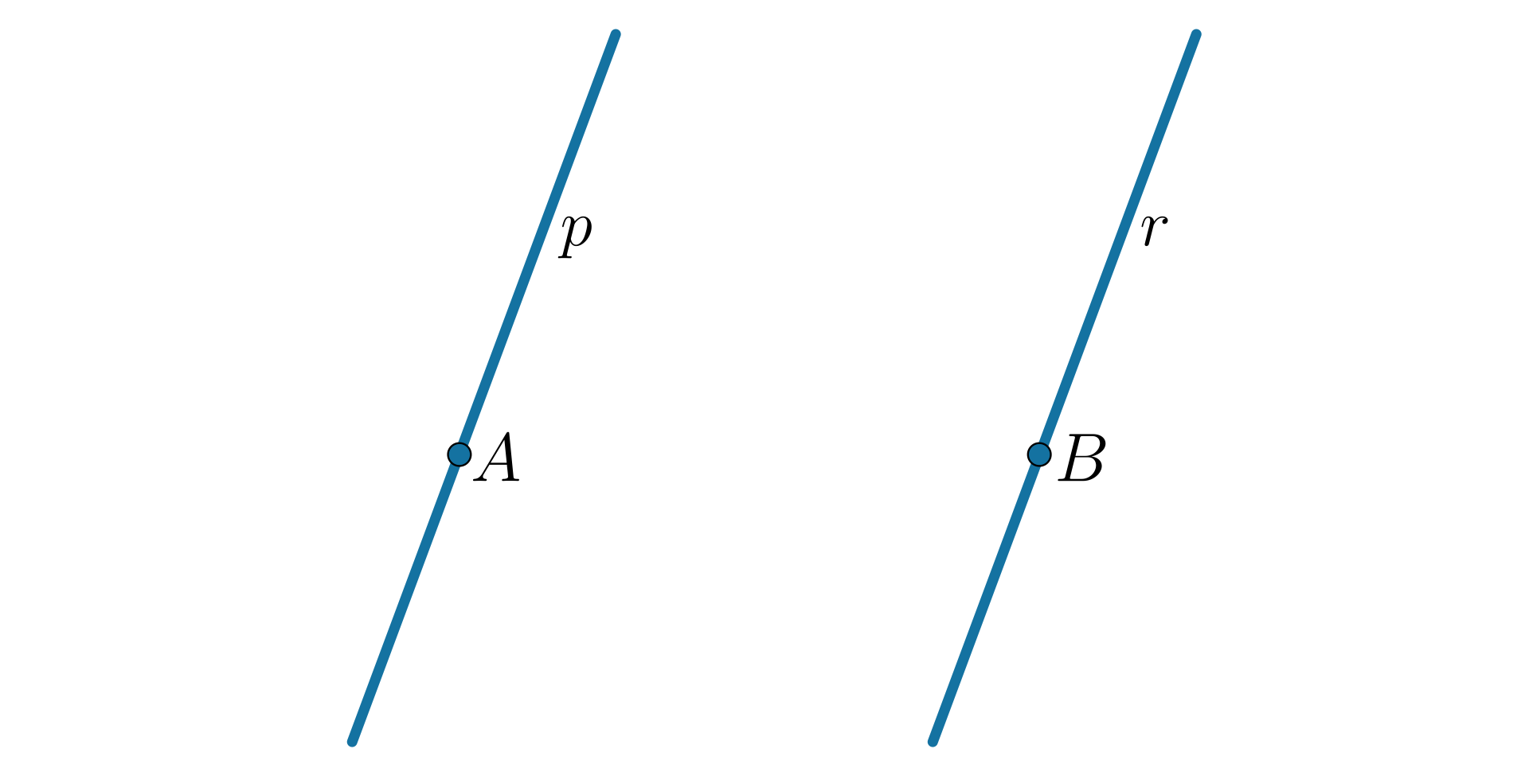
Dwie proste nazywamy równoległymi, jeśli nie mają punktów wspólnych lub mają nieskończenie wiele punktów wspólnych (pokrywają się).
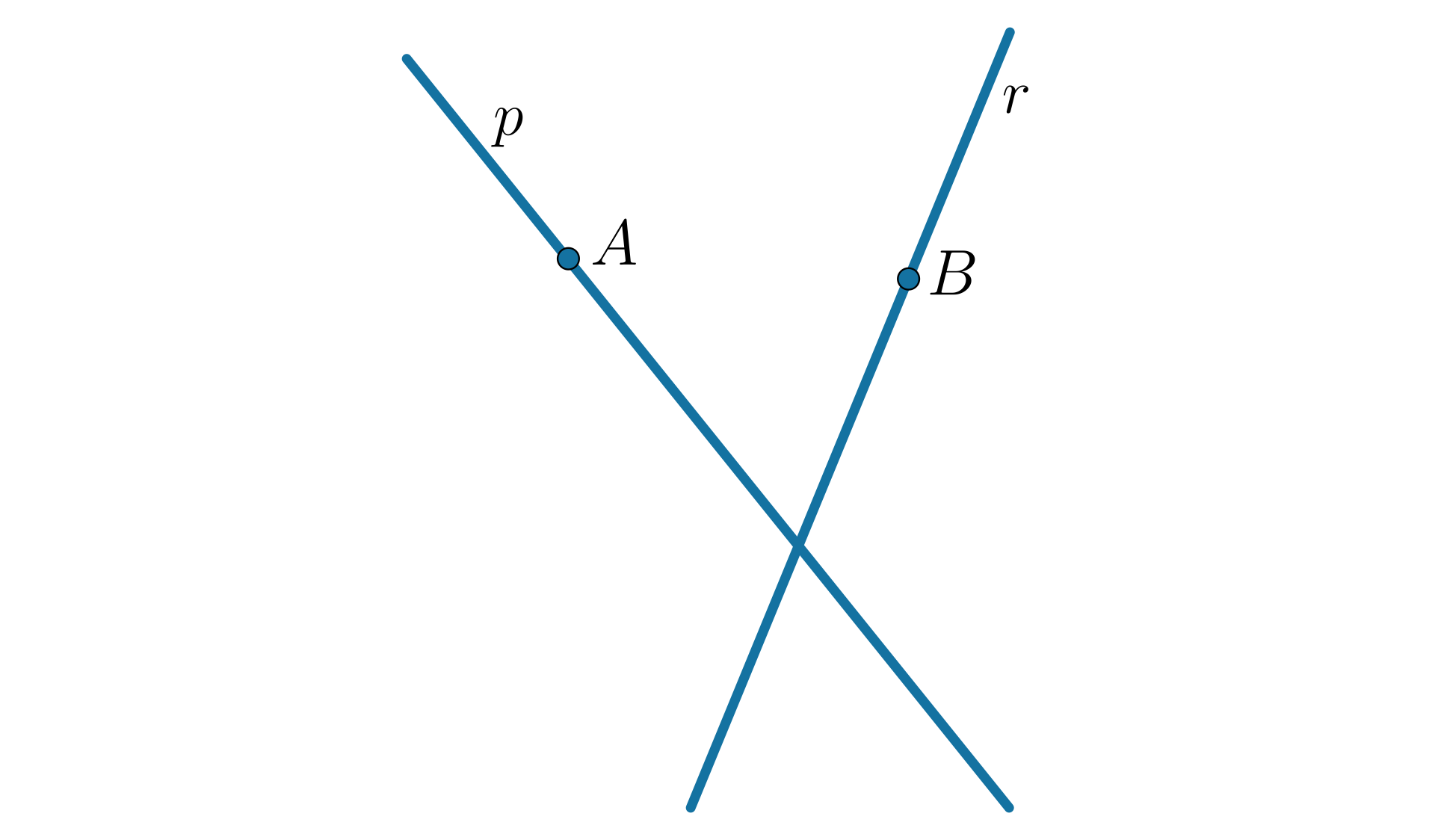
Jeśli proste mają dokładnie jeden punkt wspólny, to mówimy, że przecinają się. Takie proste nazywamy prostymi przecinającymi się.
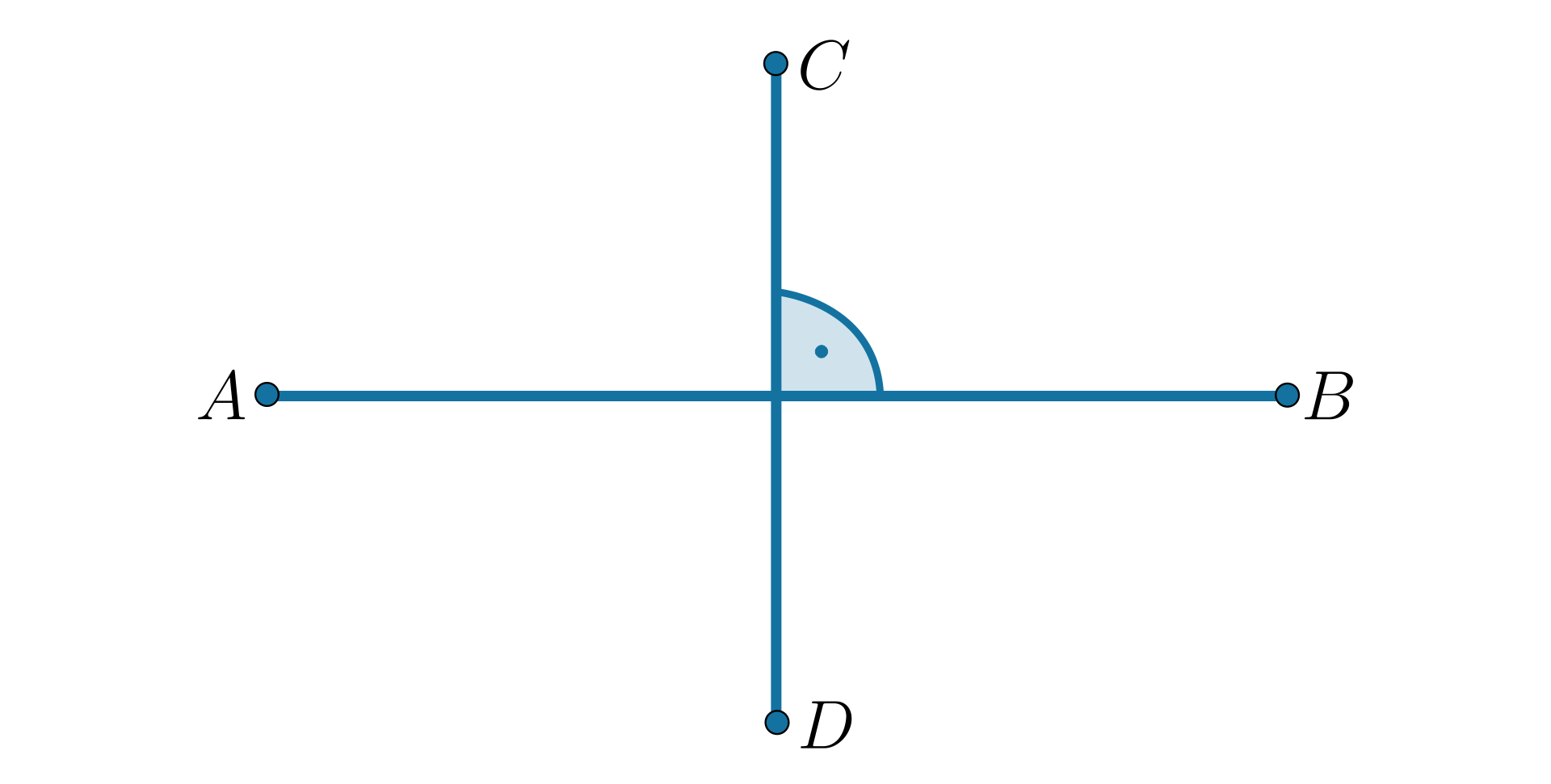
Jeśli proste przecinają się pod kątem prostym, wówczas nazywamy je prostopadłymi.
Przedstawmy konstrukcję prostej prostopadłej do danej prostej, poprowadzonej przez dany punkt.
Rozważymy dwa przypadki – punkt nie leży na danej prostej i punkt leży na prostej.
Przypadek
Dana jest prosta i punkt nieleżący na tej prostej.
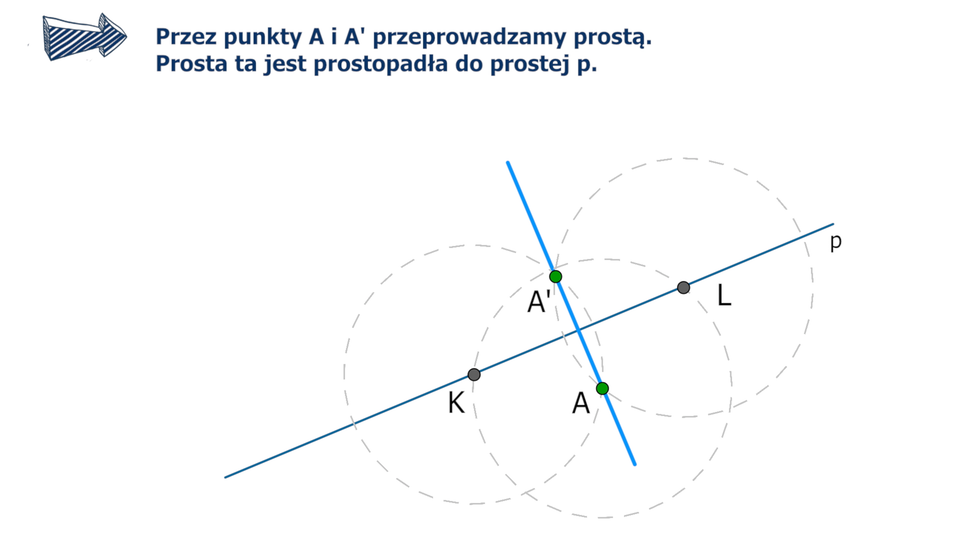
Film dostępny pod adresem /preview/resource/R1HpvGURatCjo
Animacja przedstawia w jaki sposób skonstruować prostą prostopadłą do danej prostej, która przechodzi przez punkt nieleżący na tej prostej.
Przypadek
Punkt leży na prostej .
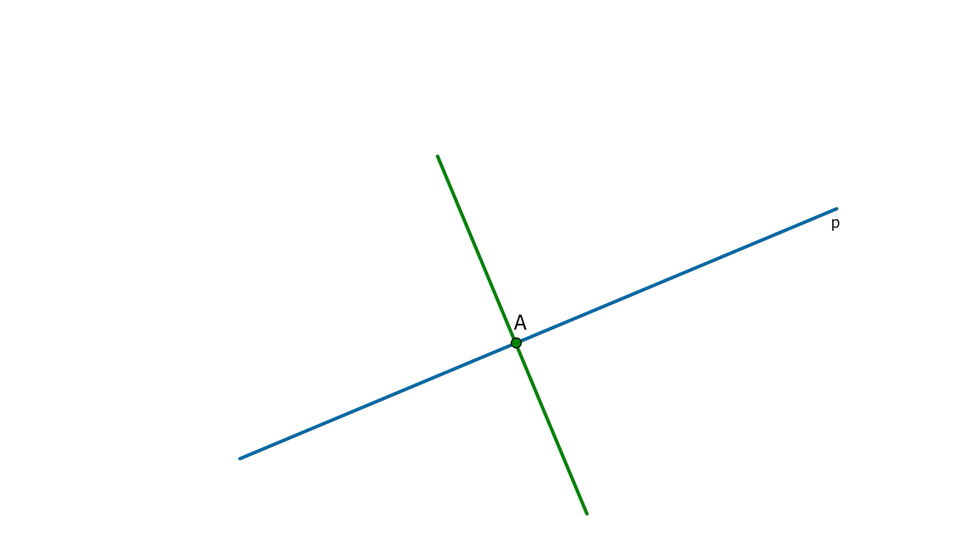
Film dostępny pod adresem /preview/resource/RSGmfTFVmejdl
Animacja przedstawia w jaki sposób skonstruować prostą prostopadłą do danej prostej, która przechodzi przez punkt leżący na tej prostej.
Przedstawmy teraz konstrukcję prostych równoległych.
Dana jest prosta i punkt nieleżący na tej prostej. Skonstruujemy prostą równoległą do prostej , przechodzącą przez punkt .
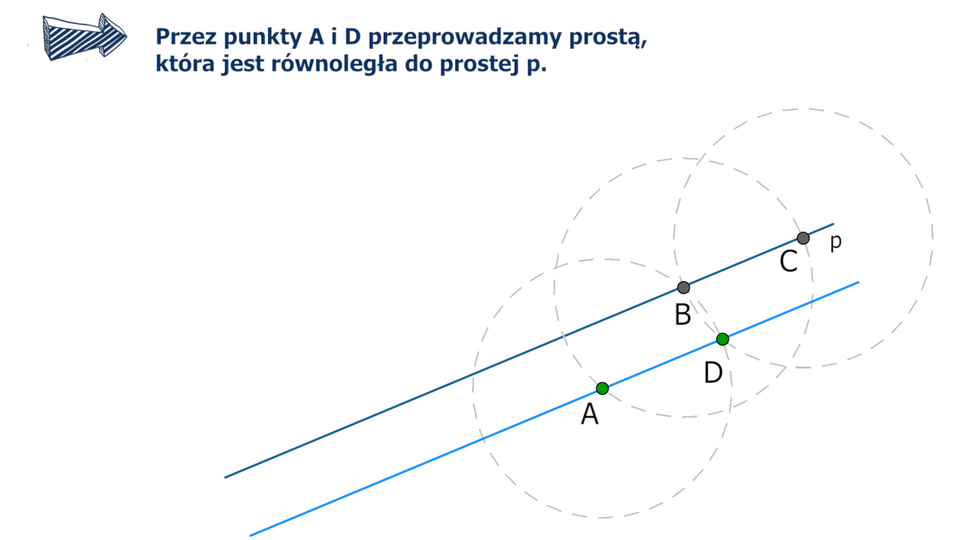
Film dostępny pod adresem /preview/resource/RoHDFdRSBznua
Animacja przedstawia w jaki sposób skonstruować prostą równoległą do danej prostej, która przechodzi przez wyznaczony punkt.
Ile prostych przechodzi przez dany punkt? A przez dwa różne punkty?

Film dostępny pod adresem /preview/resource/RBI2aJHVOCaS2
Animacja pokazuje, że przez jeden punkt przechodzi nieskończenie wiele prostych.
Przez jeden punkt przechodzi nieskończenie wiele prostych.
Przez dwa różne punkty przechodzi dokładnie jedna prosta.
Półpłaszczyzna
Prosta dzieli płaszczyznę na dwie części. Każdą z nich wraz z tą prostą nazywamy półpłaszczyzną. Prosta ta jest brzegiem każdej z tych półpłaszczyzn.
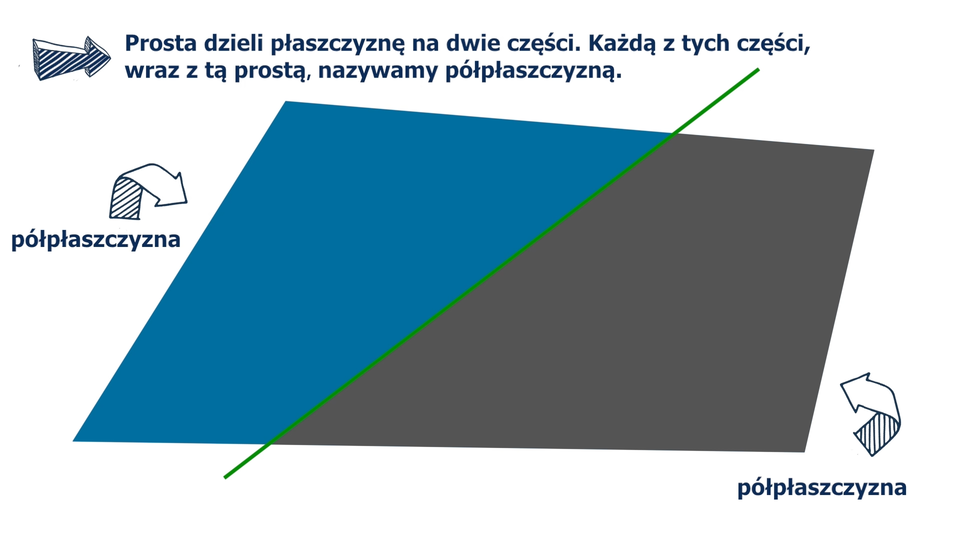
Film dostępny pod adresem /preview/resource/R15kA8mRgQdOI
Animacja przedstawia czym jest półpłaszczyzna.
Na ile części dwie lub trzy proste mogą podzielić płaszczyznę? Spróbuj wyobrazić sobie proste tak, aby podzieliły płaszczyznę na: dwie, trzy, cztery, pięć, sześć, siedem lub osiem części. Czy w każdym przypadku jest to możliwe?
Jak myślisz – na ile części dwie proste mogą podzielić płaszczyznę? A trzy proste? Sprawdź swoje przypuszczenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dd69jSpNE
Jaka jest najmniejsza, a jaka największa liczba części, na które trzy różne proste mogą podzielić płaszczyznę?
Półprosta, odcinek
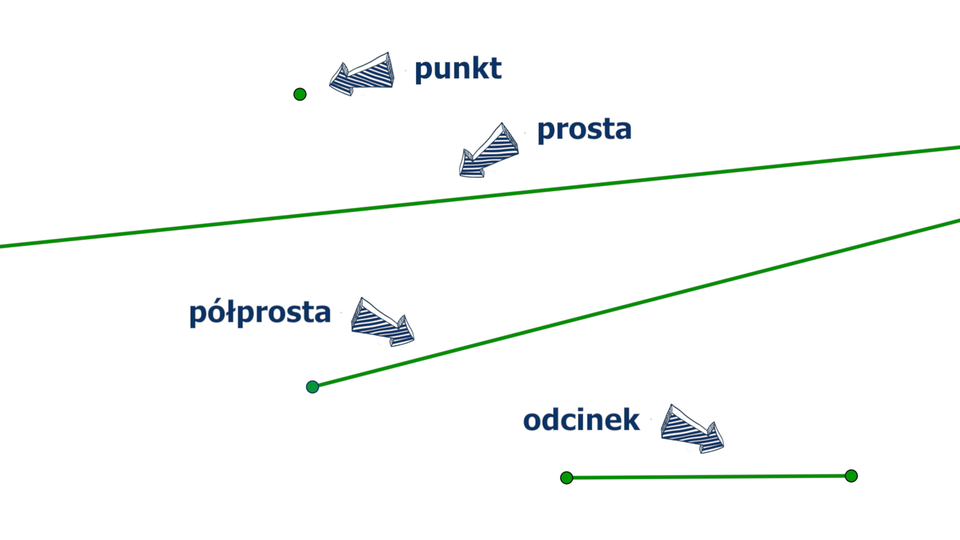
Film dostępny pod adresem /preview/resource/R3rsx0mubZk0F
Animacja przedstawia podstawowe figury geometryczne.
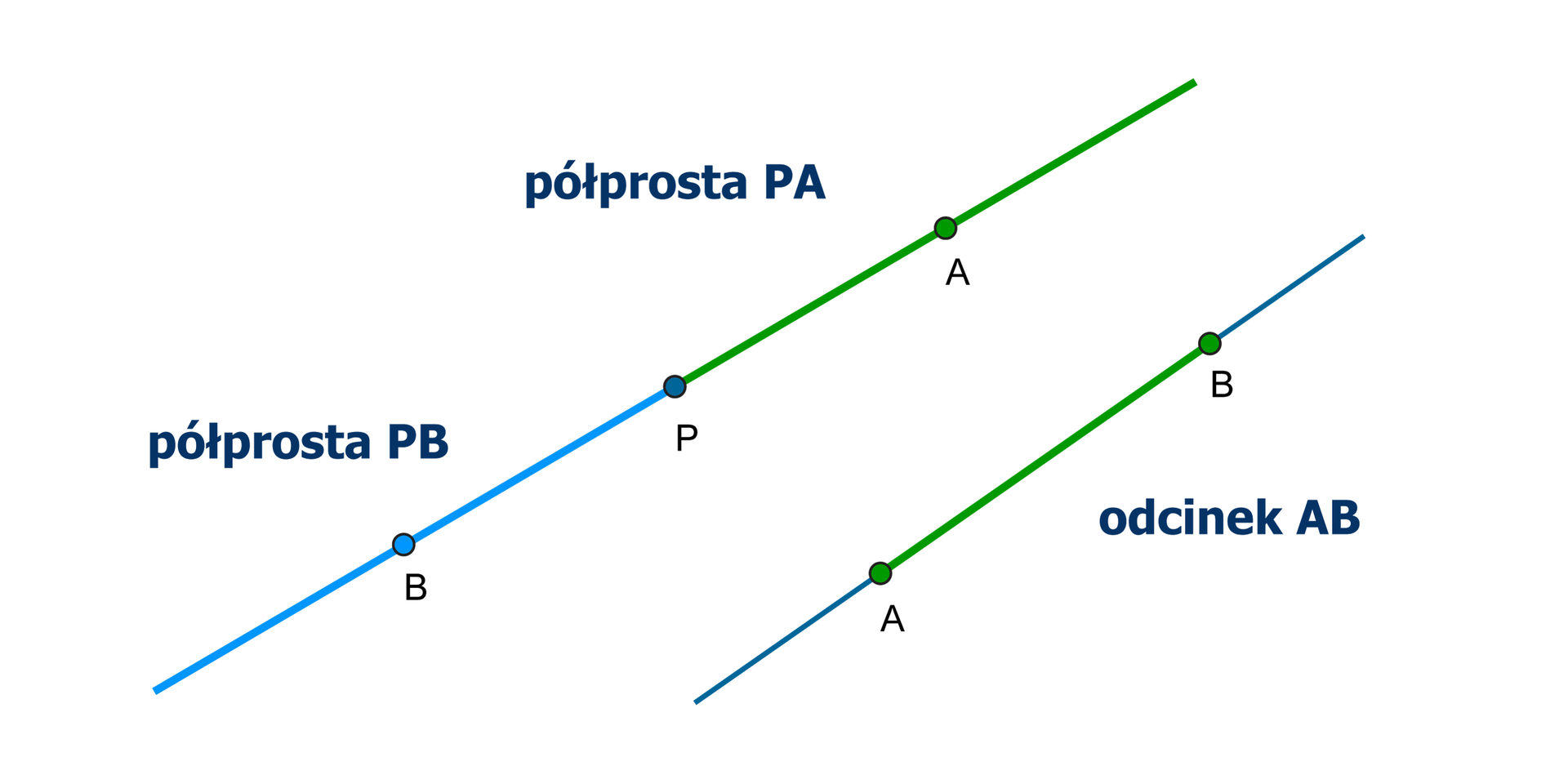
Punkt leżący na prostej dzieli ją na dwie części. Każdą z tych części, wraz z tym punktem, nazywamy półprostą. Punkt ten jest początkiem każdej z półprostych.
Część prostej zawartej między dwoma punktami, wraz z tymi punktami, to odcinek.
Zmieniaj położenie punktów i na prostej tak, aby otrzymać prostą, odcinek, półprostą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dd69jSpNE
Zapoznaj się z definicją prostej i półprostej.
Prosta - linia prosta nieograniczona z obu stron.
Półprosta - część prostej ograniczona z jednej strony punktem tej prostej, a z drugiej strony nieograniczona.
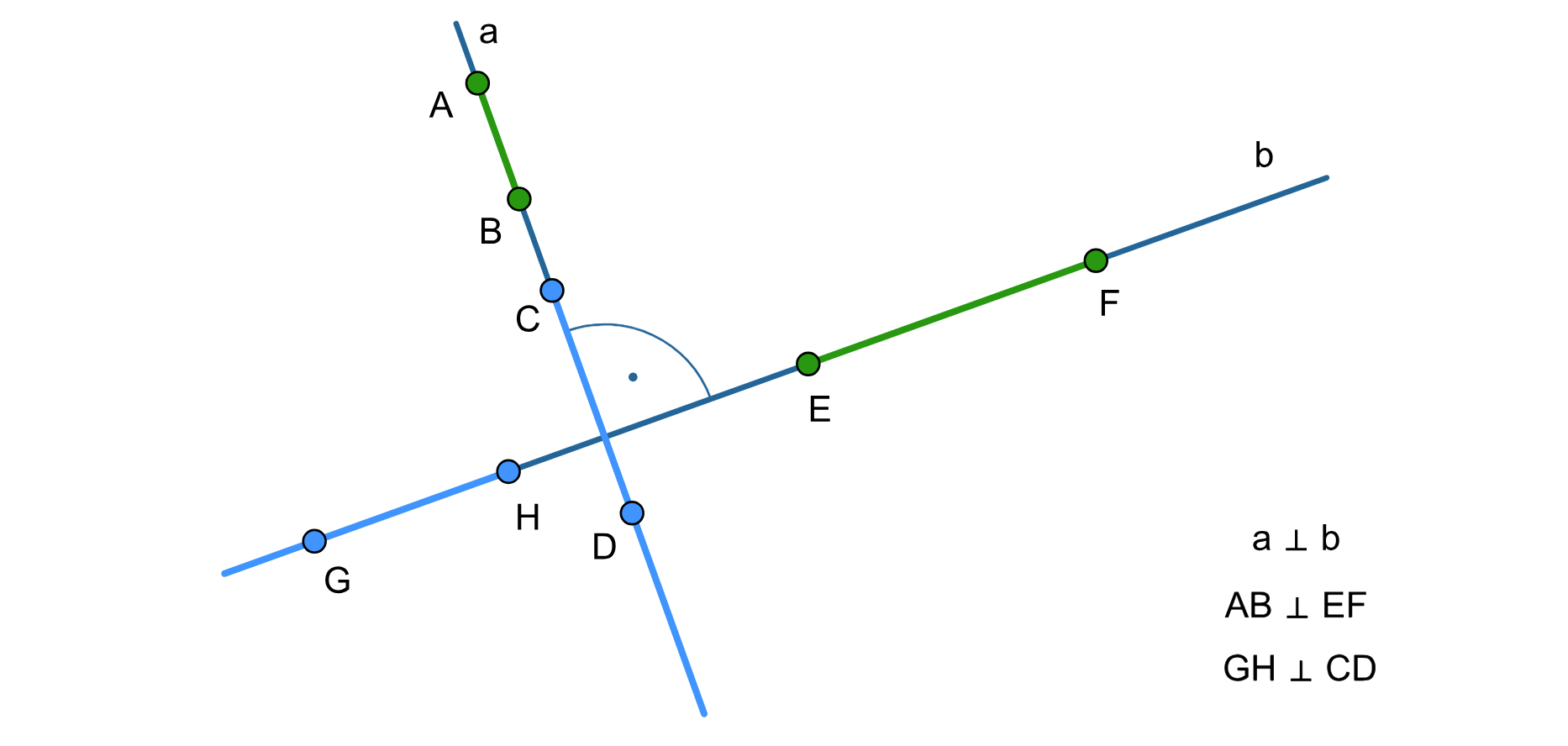
Obserwując położenie prostych i odcinków zawartych w prostych prostopadłych, zauważamy, że wszystkie półproste i odcinki zawarte w jednej z prostych prostopadłych są prostopadłe do każdej półprostej i każdego odcinka zawartych w drugiej prostej.
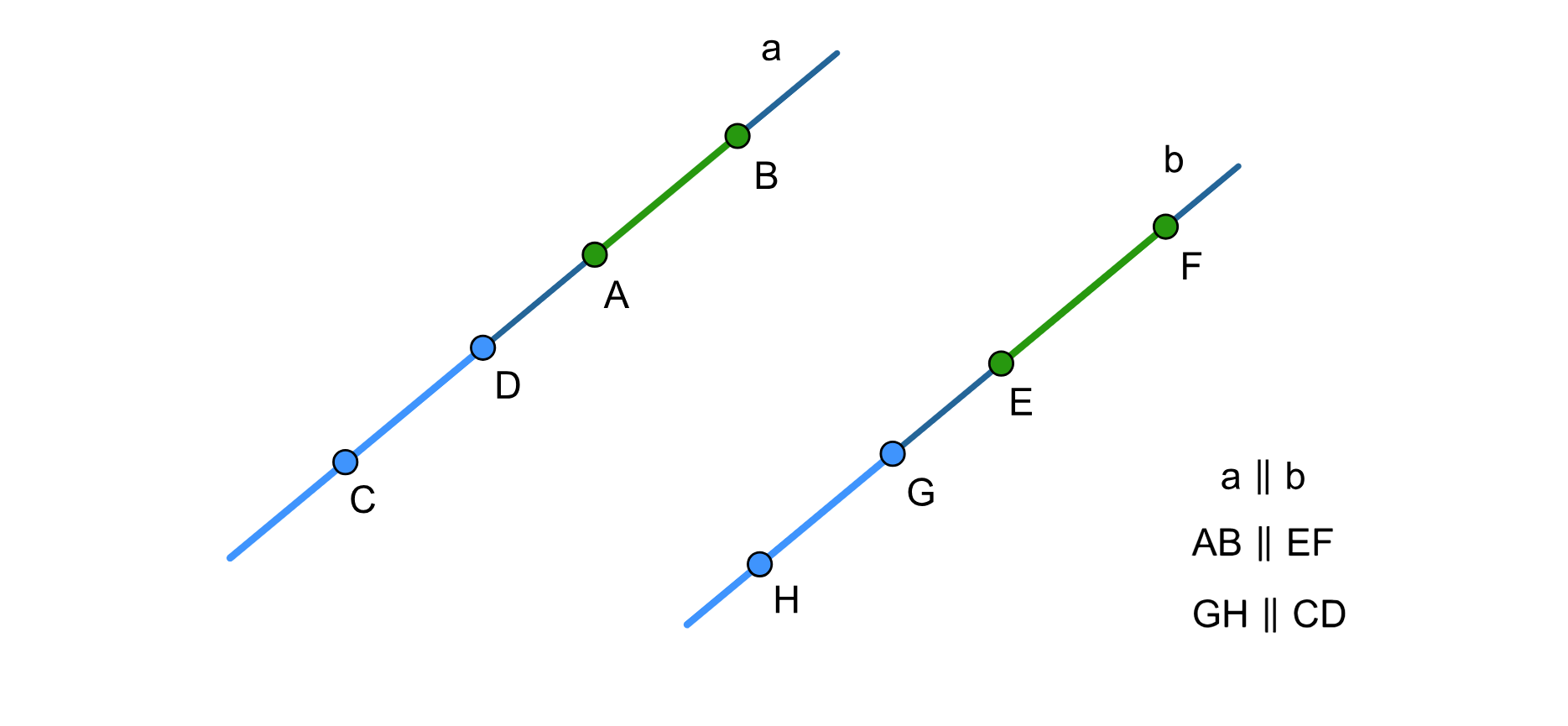
Podobnie, wszystkie półproste i odcinki zawarte w jednej z prostych równoległych są równoległe do każdej półprostej i każdego odcinka zawartych w drugiej prostej.
Łamana
Narysuj otwartą kopertę. Nie odrywaj ołówka od papieru i nie prowadź go dwa razy po tym samym odcinku (oprócz początku i końca odcinka).
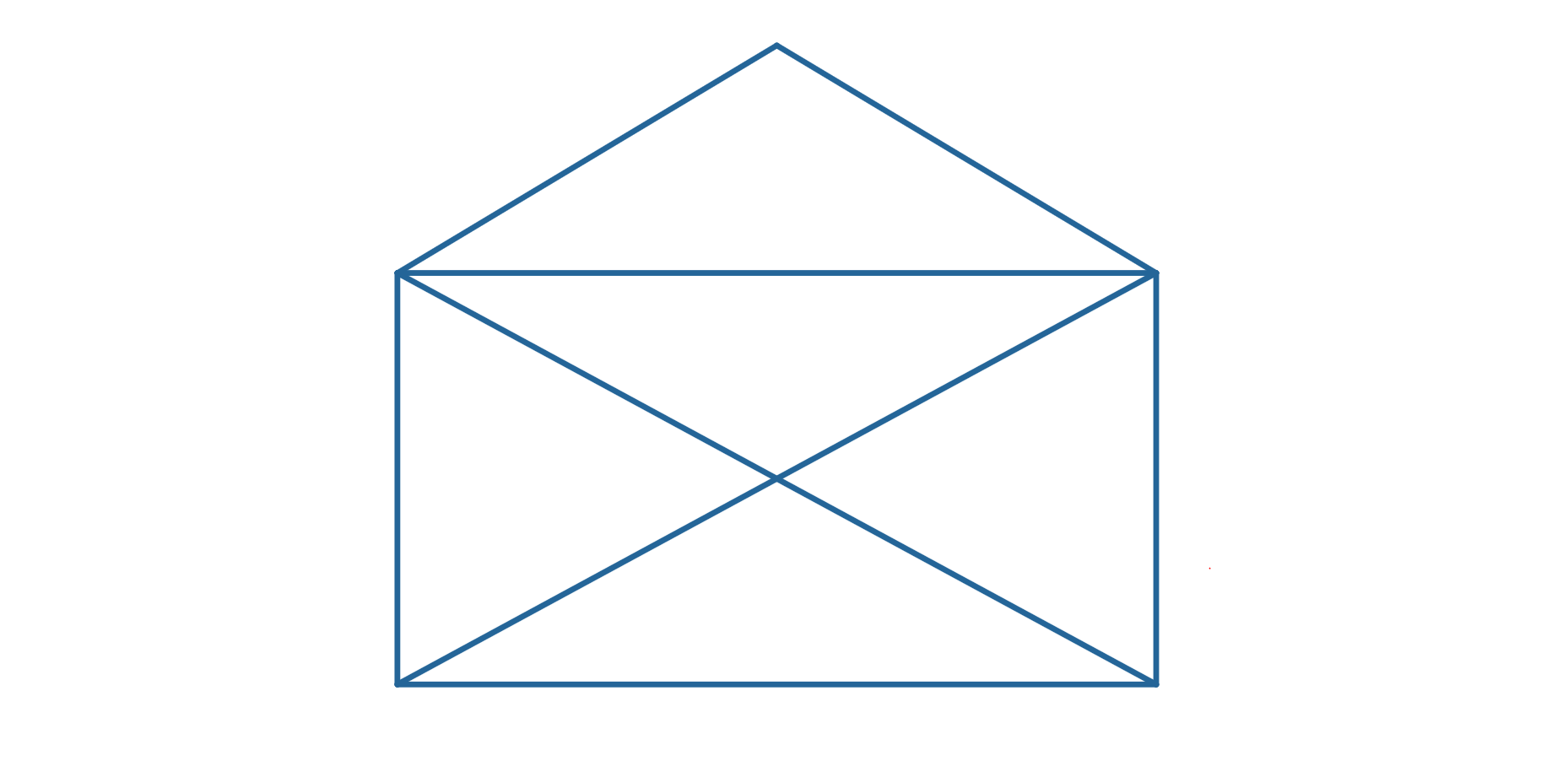
Wyobraź sobie łamaną w kształcie otwartej koperty. Czy nie odrywając ołówka od papieru i rysując jedną linię tylko jeden raz, można narysować taką łamaną?
Łamana to figura zbudowana z odcinków w ten sposób, że koniec pierwszego odcinka jest początkiem drugiego odcinka, koniec drugiego odcinka jest początkiem trzeciego itd.
Końce odcinków – wierzchołki łamanej.
To jest łamana otwarta . Ma ona wierzchołków.
R11o7FmoFudAS1 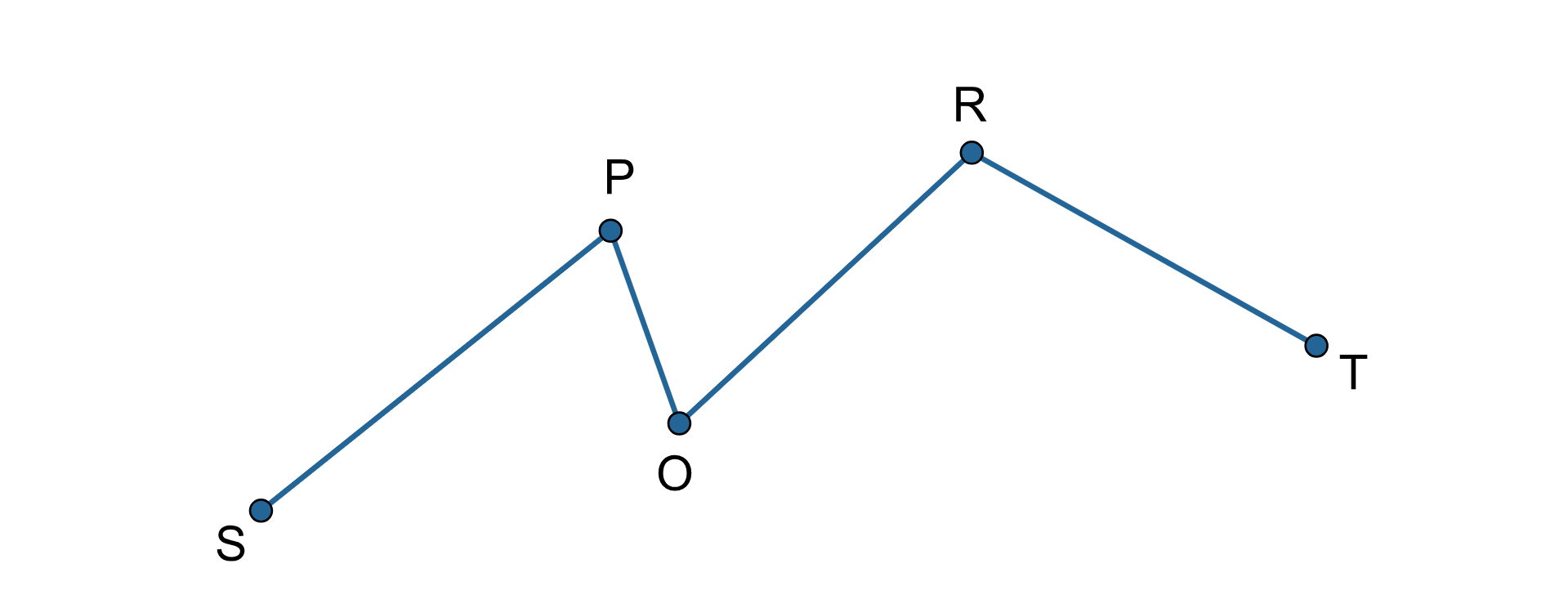 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.To jest łamana zamknięta .
R14Dt3AkOsRBK1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Figury na rysunku zbudowane są z odcinków. Każdą z nich można narysować, nie odrywając ołówka od kartki papieru i nie rysując drugi raz po tej samej linii; są to przykłady łamanych.
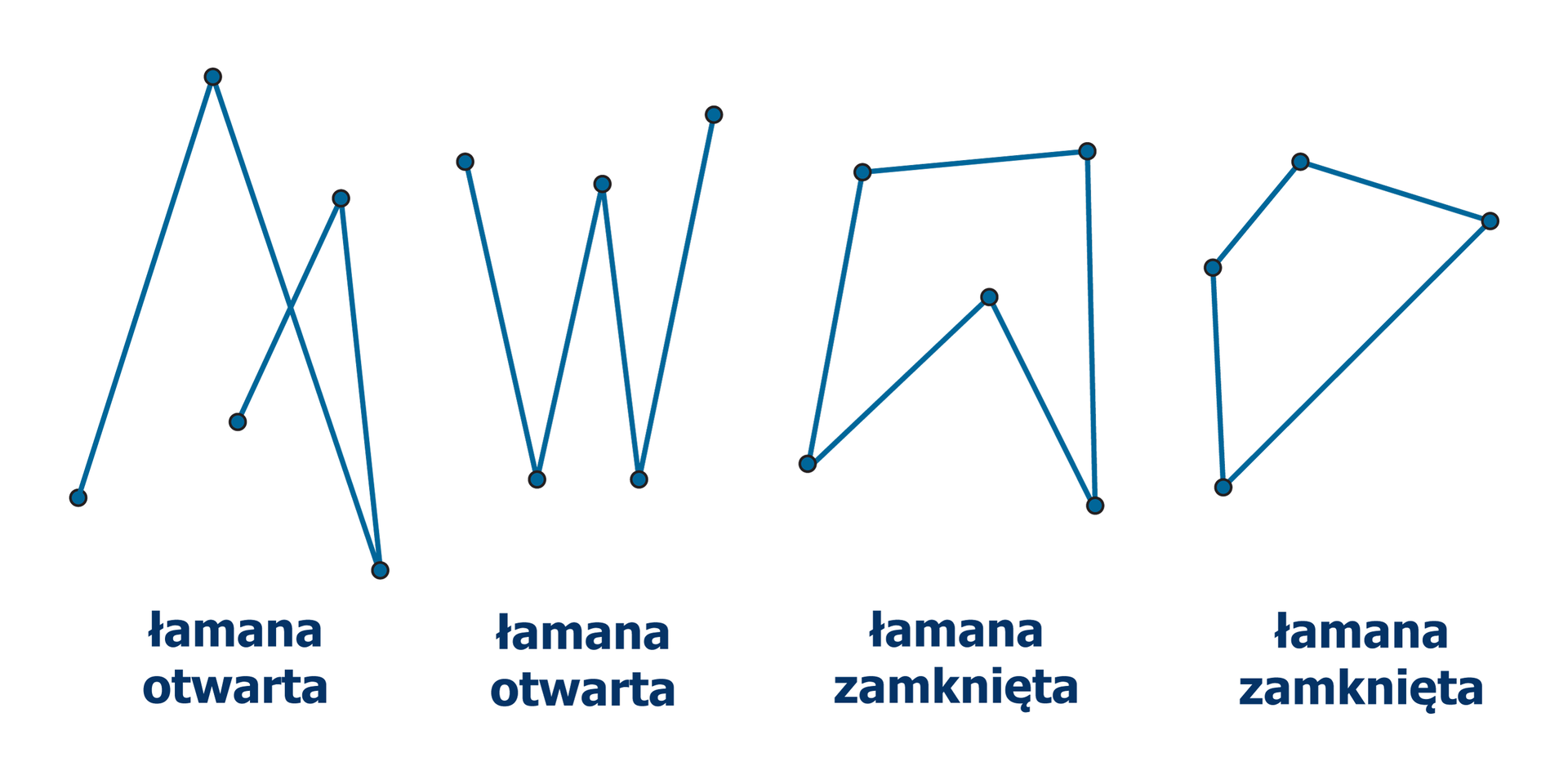
Czym różni się łamana zamknięta od otwartej?
Dlaczego figury przedstawione na rysunku nie są łamanymi?
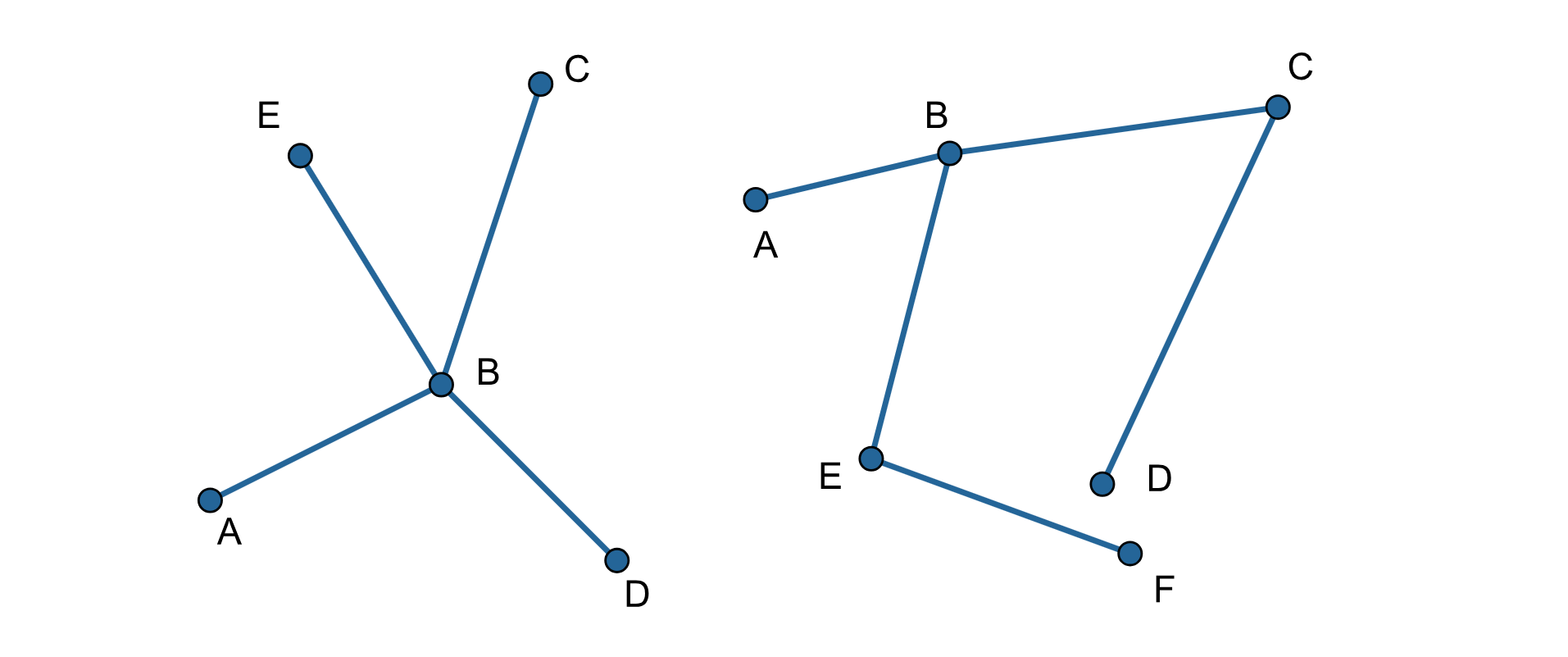
Figury nie są łamanymi, ponieważ istnieją końce odcinków, które są początkami więcej niż jednego następnego odcinka.
Z pewnością wiesz, że gazy zbudowane są z cząsteczek, które nieustannie się poruszają. Cząsteczka gazu porusza się po prostej do momentu zderzenia z inną cząsteczką. Zmienia wtedy kierunek ruchu aż do następnego zderzenia. Można więc przyjąć, że tor ruchu tej cząsteczki ma kształt łamanej.
Przykłady figur płaskich
Modele jakich figur płaskich zauważasz na rysunkach?
Czy rozpoznajesz wśród nich wielokąty? A okręgi? A koła?

Narysuj dwa odcinki, które
mają jeden punkt wspólny,
są prostopadłe,
są równoległe.
Opisz dwa odcinki, które
mają jeden punkt wspólny,
są prostopadłe,
są równoległe.
- Dwa odcinki, które leżą na jednej prostej mogą mieć punkty wspólne.
- Dwa odcinki, które leżą na jednej prostej są równoległe.
- Dwa odcinki, które leżą na jednej prostej mogą być prostopadłe.
- prostopadłe
- równoległe
- skośne
- przecinające się
Odpowiedź: Proste są 1. przystające, 2. prostopadłe, 3. prostopadłe, 4. równoległe, 5. trzy wspólne punkty, 6. jeden wspólny punkt, 7. cztery wspólne punkty, 8. równoległe, 9. przystające, 10. dwa wspólne punkty.
Jak położone są względem siebie proste i ?
Odpowiedź: Proste są 1. przystające, 2. prostopadłe, 3. prostopadłe, 4. równoległe, 5. trzy wspólne punkty, 6. jeden wspólny punkt, 7. cztery wspólne punkty, 8. równoległe, 9. przystające, 10. dwa wspólne punkty.
Ile punktów wspólnych mają proste i ?
Odpowiedź: Proste mają 1. przystające, 2. prostopadłe, 3. prostopadłe, 4. równoległe, 5. trzy wspólne punkty, 6. jeden wspólny punkt, 7. cztery wspólne punkty, 8. równoległe, 9. przystające, 10. dwa wspólne punkty.
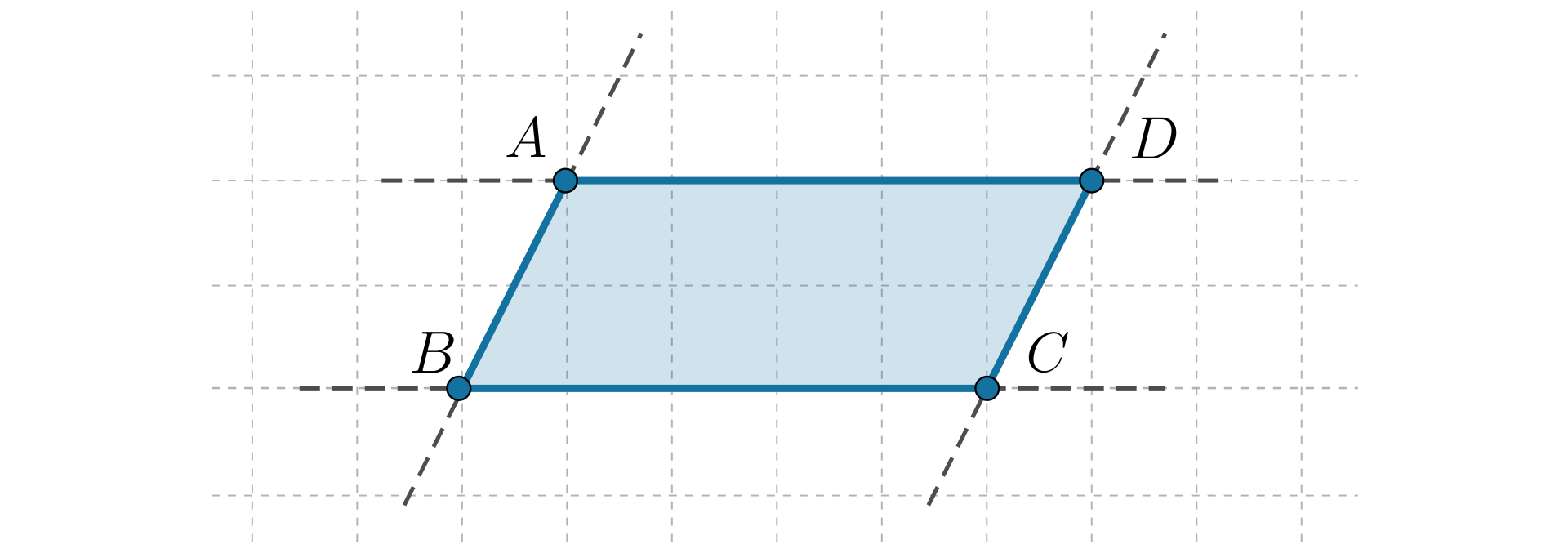
Punkt wyznacza na prostych i cztery półproste. Jak mogą być położone proste i ? Gdzie leży punkt ?
Narysuj dwa różne punkty i . Przez punkt przeprowadź prostą , a przez punkt prostą tak, aby proste i
nie miały punktów wspólnych,
przecinały się,
były prostopadłe.
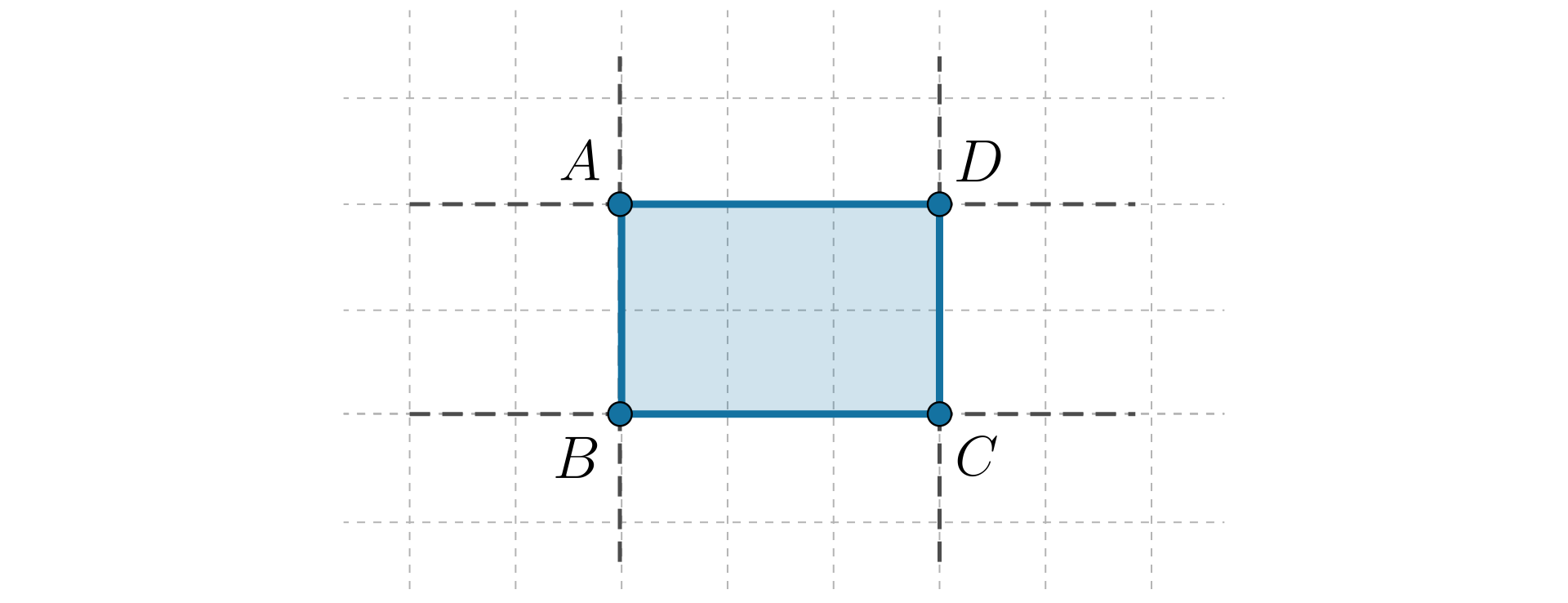
Narysuj
prostokąt.
równoległobok.
Opisz konstrukcję:
prostokąta.
równoległoboku.
Zaobserwuj, w kształcie jakich figur płaskich mogą być cienie prostopadłościanu.
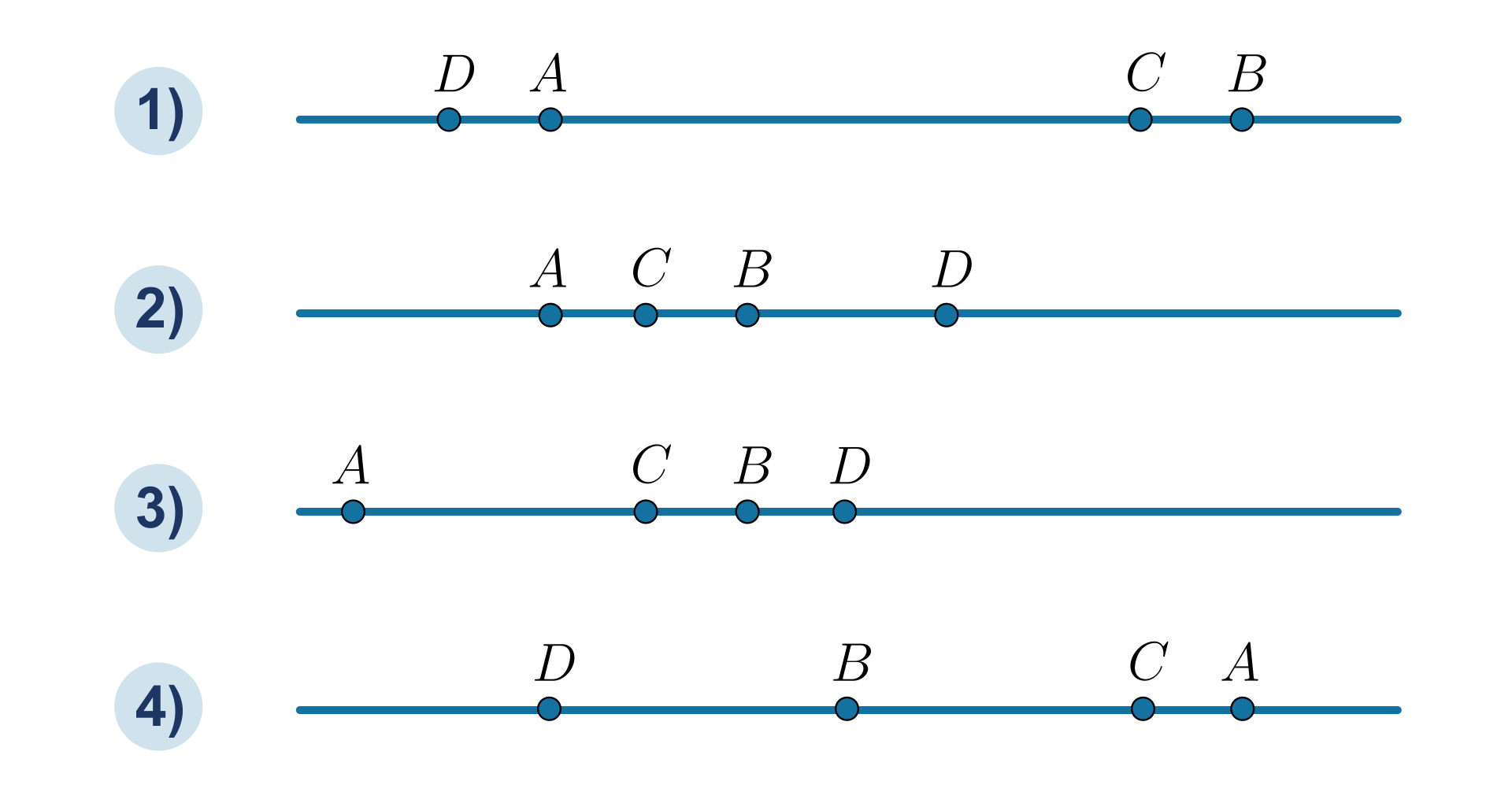
Narysuj prostą i zaznacz na niej punkty , , , tak, aby punkt leżał między punktami i . Rozpatrz różne przypadki.
Wyobraź sobie prostą i zaznaczone na niej punkty , , , tak, aby punkt leżał między punktami i . Wypisz trzy różne przypadki rozmieszczenia tych punktów.
Adam ma różne drogi powrotu ze szkoły, a po drodze przechodzi przez pewne punkty orientacyjne w mieście.
Ze szkoły do kościoła jest .
Ze szkoły do placu targowego jest .
Ze szkoły do domu babci jest .
Z placu targowego do kościoła jest .
Z placu targowego do apteki jest .
Z apteki do domu jest .
Z kościoła do domu jest .
Z domu babci do kościoła jest .
Wyznacz najdłuższą i najkrótszą drogę Adama do domu. Określ, z ilu odcinków się składa.
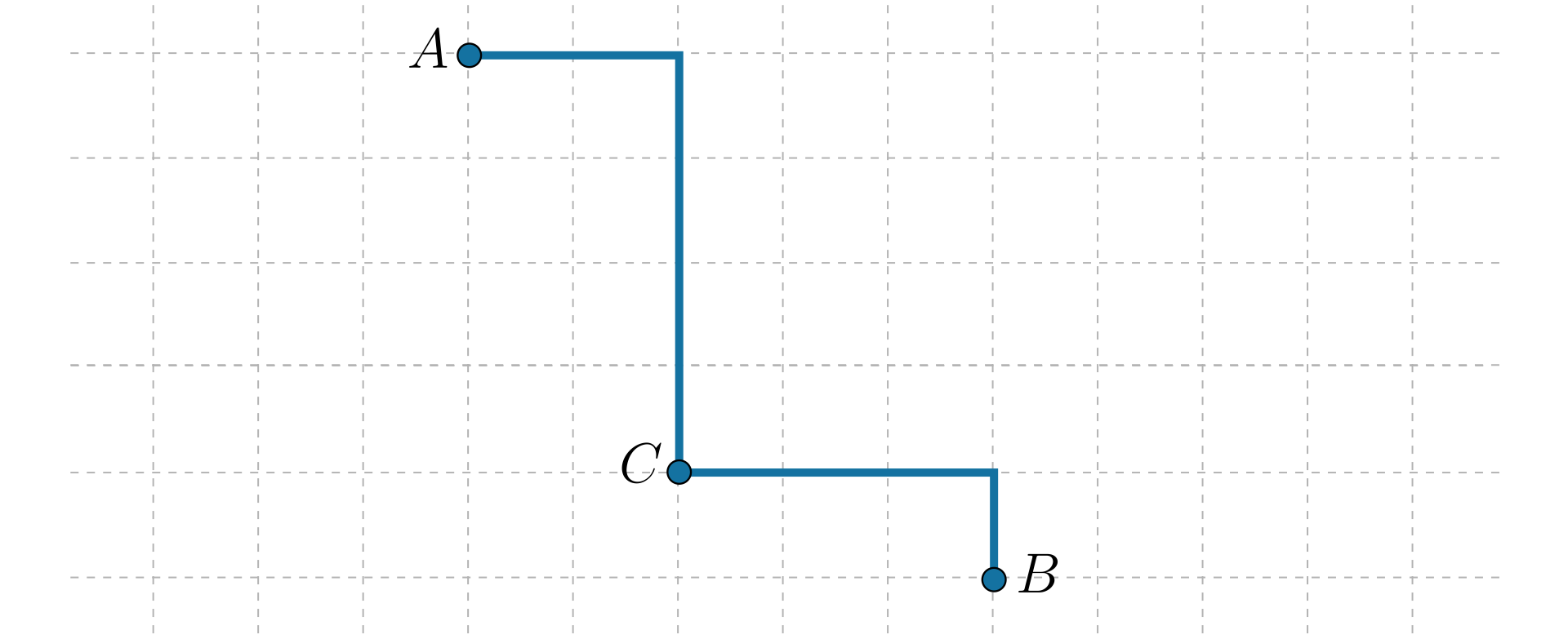
Mucha przemieszcza się z punktu do punktu . Porusza się tylko po liniach kratek w dół i w prawo. Musi przejść przez punkt . Długość jednej kratki jest równa .
Zaznacz kilka dróg, którymi może się poruszać mucha.
Znajdź długość każdej z nich.
Jaką długość ma najkrótsza z możliwych dróg?
RlCcyU270VOJZ1 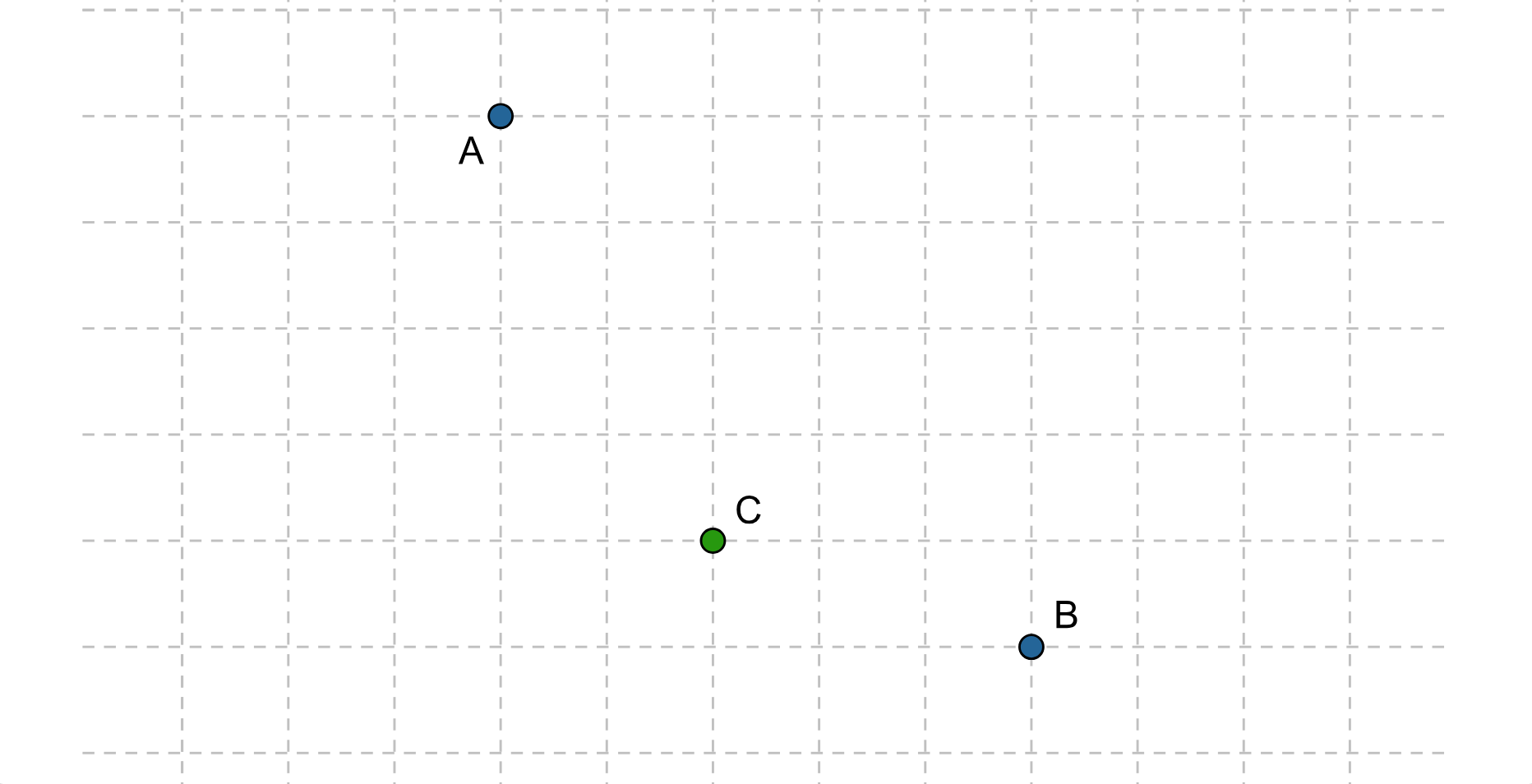 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
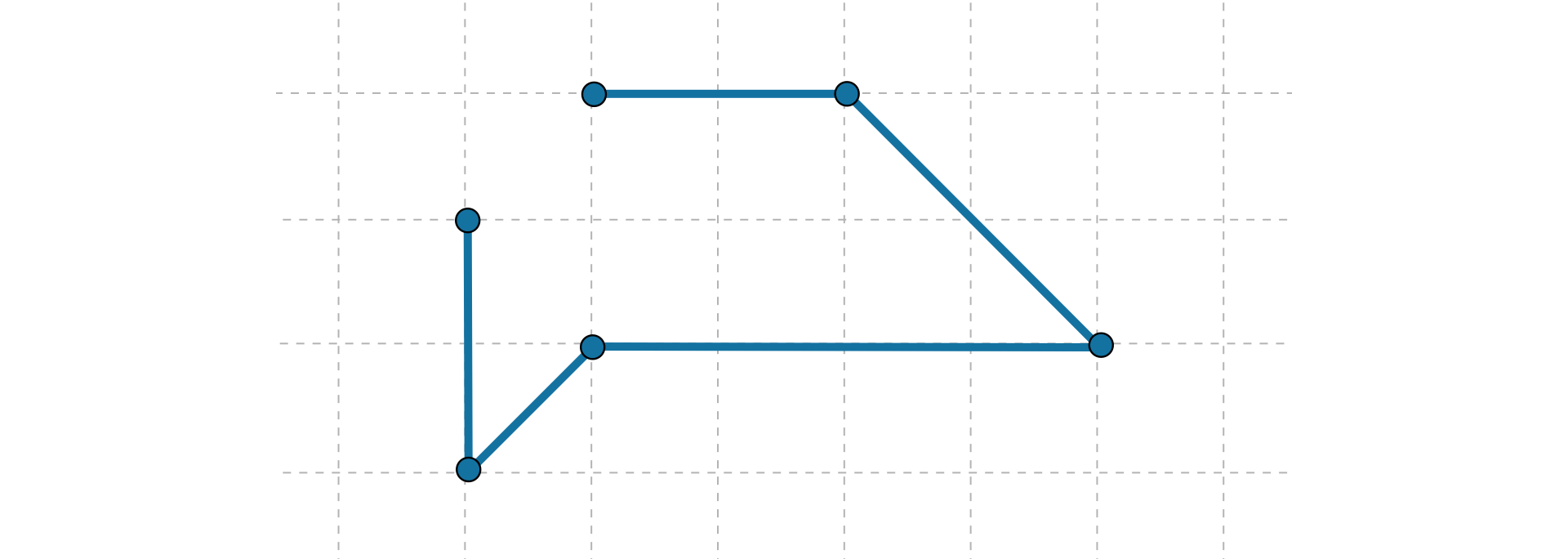
Opisz łamaną, w której
boki są prostopadłe,
dokładnie dwa boki są równoległe,
każdy bok ma inną długość,
boki są prostopadłe, ale ich długości nie są równe.
Narysuj łamaną, której
boki są prostopadłe,
dokładnie dwa boki są równoległe,
każdy bok ma inną długość,
boki są prostopadłe, ale ich długości nie są równe.
Na rysunku przedstawiono dziewięć figur oznaczonych literami od do .
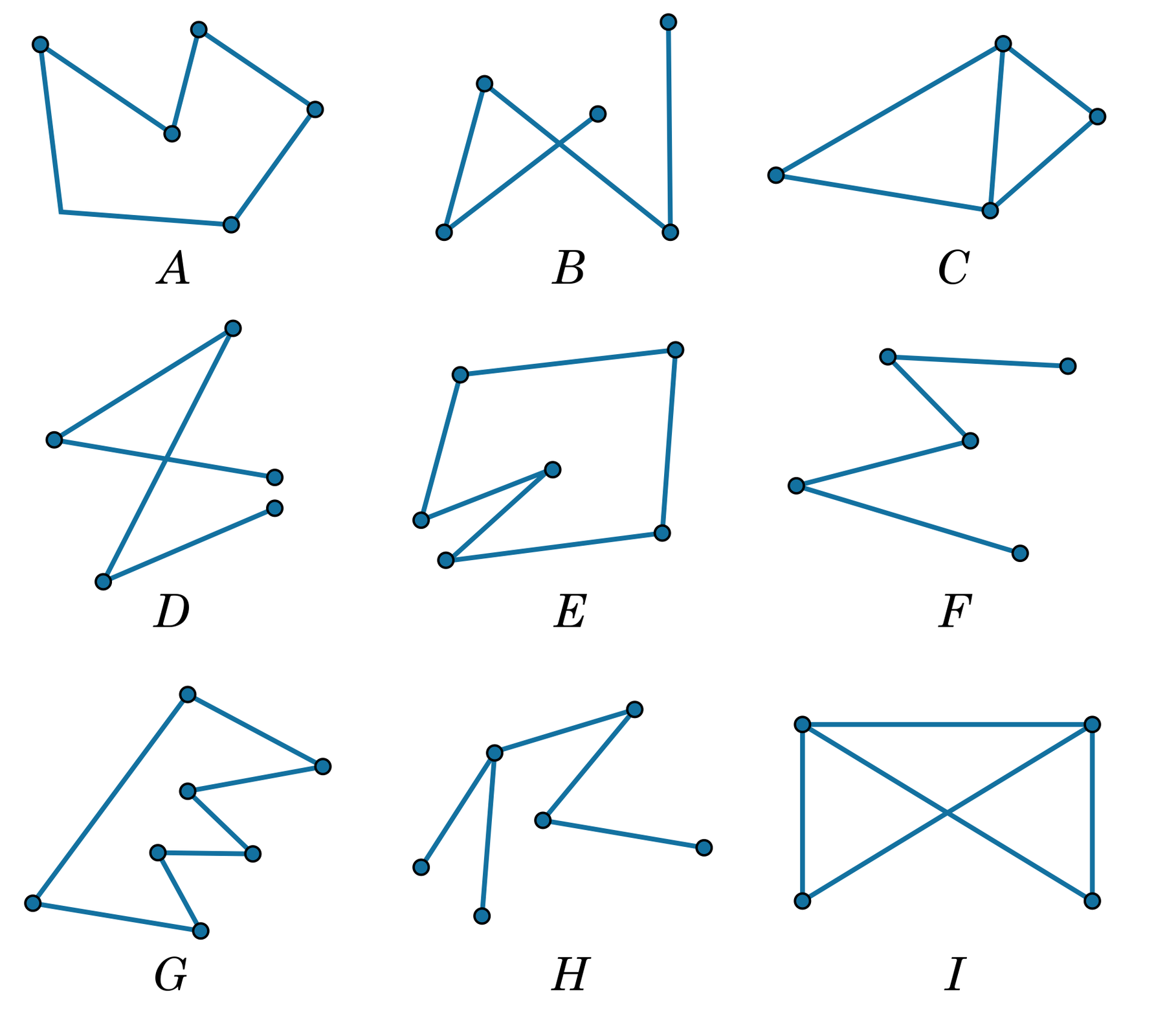
- Z odcinków długości , , można zbudować łamaną zamkniętą.
- Jeśli łamana zamknięta ma cztery boki to jej boki mogą być bokami kwadratu.
- Z odcinków długości , , można zbudować łamaną otwartą.
Znajdź informacje na temat Gasparda Monge i zastosowania wynalezionej przez niego metody rzutowania obiektów na lub płaszczyzny wzajemnie do siebie prostopadłe.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.