1. Ładunki elektryczne i ich oddziaływanie. Ładunek elementarny
Czy wiesz, dlaczego podczas zdejmowania swetra włosy się unoszą, a podaniu ręki czasami towarzyszy iskra? Dlaczego koty zazwyczaj nie lubią głaskania pod włos? Jeśli chcesz wiedzieć, dlaczego tak się dzieje, czytaj dalej.

występujące w przyrodzie oddziaływania bezpośrednie oraz na odległość;
wzajemność oddziaływań;
skutki oddziaływań.
Ich opracowanie znajdziesz materiale Rodzaje oddziaływań i ich skutki. Wzajemność oddziaływań.
wskazywać przykłady elektryzowania się ciał;
podawać definicję elementarnego ładunku elektrycznego;
opisywać jakościowo i ilościowo oddziaływania między ładunkami;
omawiać budowę wybranego pierwiastka chemicznego lub jonu;
opisywać i wyjaśniać wyniki doświadczeń dotyczących elektryzowania ciał.
Oddziaływanie ciał naelektryzowanych
Właściwości i zachowanie ciał obdarzonych określonym ładunkiem elektrycznym badano już w starożytności. Na przełomie i wieku p.n.e. grecki filozof i matematyk Tales z Miletu zaobserwował tzw. efekt bursztynu. Zauważył, że bursztyn (gr. ēlektron) potarty suknem przyciąga niektóre lekkie ciała, np. piórka, drewniane wiórki, suche źdźbła trawy. Później okazało się, że podobnych zjawisk jest więcej. Obecnie wiadomo, że istnieje jeszcze wiele ciał wykazujących podobne właściwości elektrostatyczne. Często są to przedmioty użytku codziennego, np. koc, sweter, grzebień, balon itp.
Zanim zaczniesz wykonywać doświadczenie zapoznaj się z załączonym materiałem filmowym.

Film dostępny pod adresem /preview/resource/R1SoNZFU12D14
Film dotyczący oddziaływań elektrostatycznych balonów i koca.
Jakościowe określenie czynników wpływających na wielkość oddziaływań elektrostatycznych.
sweter (może być koc);
dwa balony;
nitka ( kawałki po ok. );
nożyczki.
Oddziaływanie balon – balon.
Nadmuchaj balony i zwiąż je nitką tak, aby nie uciekało z nich powietrze.
Potrzyj pierwszym balonem o sweter (staraj się trzymać balon tylko za nitkę). To samo zrób z drugim balonem.
Spróbuj zbliżyć balony do siebie.
Zapisz swoje spostrzeżenia.
Oddziaływanie balon – sweter.
Potrzyj jednym z balonów o sweter.
Odsuń balon od swetra (na odległość ok. ).
Zbliż balon do swetra.
Zapisz swoje spostrzeżenia.
Powtórz punkty i , ale tym razem potrzyj balony o sweter znacznie intensywniej niż poprzednio.
Zapisz swoje spostrzeżenia.
Dwa naelektryzowane balony wzajemnie się odpychają, natomiast balon i sweter się przyciągają. Wzajemne oddziaływanie między balonem a swetrem zależy zarówno od stopnia ich naelektryzowania, jak i odległości między nimi. Intensywniejsze potarcie wzmacnia efekt.
Zaobserwowane zjawiska nasuwają przypuszczenie, że przedmioty wykorzystane w doświadczeniu uzyskały jakąś nową właściwość, która jest odpowiedzialna za ich wzajemne oddziaływanie. Aby ją opisać, fizycy wprowadzili wielkość fizyczną nazywaną ładunkiem elektrycznym. Przyjęto, że występują dwa rodzaje ładunków – dodatnie (oznaczane znakiem ) i ujemne (oznaczane znakiem ). Ładunki tego samego znaku (jednoimienne) się odpychają, a ładunki różnych znaków (różnoimienne) się przyciągają. Za pomocą pojęcia ładunku elektrycznego można wytłumaczyć zaobserwowane zjawisko. Ładunki zgromadzone na balonie i swetrze są różnoimienne, więc oba przedmioty się przyciągają. Na powierzchni balonów gromadzą się ładunki jednoimienne, które powodują, że te ciała się odpychają.
Ładunek zgromadzony na powierzchni ciał decyduje o kierunku oddziaływania. Oczywiście, w życiu codziennym ładunków elektrycznych nie widać gołym okiem, za to można z łatwością zaobserwować skutki ich wzajemnych oddziaływań. Ilość i znak zgromadzonego ładunku elektrycznego pozwalają na dokładne określenie tych oddziaływań. Jednostką ładunku elektrycznego jest kulomb, który oznaczamy symbolem . Jego nazwa pochodzi od nazwiska Charles'a Augustina de CoulombaCharles'a Augustina de Coulomba – francuskiego uczonego, który jako pierwszy określił wielkość siły oddziaływania między ładunkami elektrycznymi. Kulomb jest dużą jednostką, dlatego w praktyce stosuje się podwielokrotności kulomba – milikulomb i mikrokulomb.
Im większy ładunek znajduje się na powierzchni ciał i im mniejsza jest odległość między nimi, tym większe staje się wzajemne oddziaływanie (odpychające lub przyciągające) jednego na drugie. Siłę działającą między ciałami naelektryzowanymi nazywamy siłą elektrostatyczną (elektryczną) lub siłą Coulomba.
Przelicz jednostki ładunku elektrycznego.
5 mC = ............ C
146 mC = ............ C
853 µC = ................ C
29 µC = ................ C
Dokończ zdanie, wybierając poprawne odpowiedzi.
Ładunek o wartości jest: Możliwe odpowiedzi: 1. mniejszy od kulomba., 2. większy od kulomba., 3. równy ., 4. równy .
Jednostką ładunku elektrycznego jest kulomb (C). Ładunek o wartości 18 μC jest
- mniejszy od kulomba.
- większy od kulomba.
- równy 0,018 C.
- równy 0,000018 C.
W roku sterowiec Hindenburg spłonął podczas lądowania na lotnisku Lakehurst w stanie New Jersey. Podejrzewa się, że przyczyną katastrofy mógł być ładunek elektryczny, który zgromadził się na powłoce sterowca. Zginęło wówczas pasażerów i członków załogi, a także główny członek załogi naziemnej – kapitan Ernst Lehmann.
Budowa atomu
Aby wyjaśnić oddziaływania elektryczne, trzeba poznać mikroświat, czyli świat atomów. Każdy pierwiastek chemiczny składa się z takich samych atomów. Każdy atomatom jest obojętny elektrycznie, tzn. ma jednakową liczbę ładunków dodatnich i ujemnych.

Film dostępny pod adresem /preview/resource/R1Z9bQZoAHDUF
Animacja dotycząca budowy atomu wodoru.
Powyższa animacja przedstawia tzw. model planetarny atomu wodoru, stworzony na początku wieku. W centrum atomu znajduje się jądro atomowe, które jest zbudowane z protonów i neutronów. Wokół jądra krążą elektrony. Dzięki oddziaływaniu elektrycznemu atom się nie rozpada, a jądro przyciąga elektrony. Protony i elektrony są obdarzone ładunkami elektrycznymi o tej samej wartości, ale o przeciwnych znakach. Ładunek elektryczny protonów jest dodatni, a elektronów – ujemny. Neutrony są cząstkami obojętnymi elektrycznie.
Model planetarny atomu pozwalał wyjaśnić jedynie niektóre zjawiska mikroświata. Dalsze badania wymagały stworzenia bardziej skomplikowanych modeli. Dowiesz się o nich więcej podczas nauki w szkole średniej.
Z układu okresowego pierwiastków możesz odczytać informację o liczbie protonów, elektronów i neutronów każdego znanego nam pierwiastka chemicznego.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pqvz8S0S5
Przykładowo zapis
oznacza, że potas () ma protonów (jest to liczba atomowa lub liczba porządkowa). Pierwiastek jest obojętny elektrycznie, dlatego liczba jego elektronów jest także równa ; liczba niesie informację o liczbie składników jądra (jest to tzw. liczba masowa). Aby ustalić liczbę neutronów, od liczby masowej (czyli łącznej liczby protonów i neutronów w jądrze) należy odjąć liczbę atomową:
Uzupełnij puste miejsca.
to atom chloru. W jego skład wchodzi: ............ protonów , ............ elektronów i ............ neutronów.
to atom żelaza. Atom ten zbudowany jest z: ............ protonów , ............ elektronów i ............ neutronów.
Jeśli do atomu zostanie dostarczony jeden lub kilka elektronów, to staje się on jonem ujemnymjonem ujemnym. Jon ujemny ma więcej elektronów niż protonów. Jeśli natomiast od atomu zostanie odłączony jeden bądź kilka elektronów, to staje się on jonem dodatnimjonem dodatnim. Jon dodatni ma więcej protonów niż elektronów.
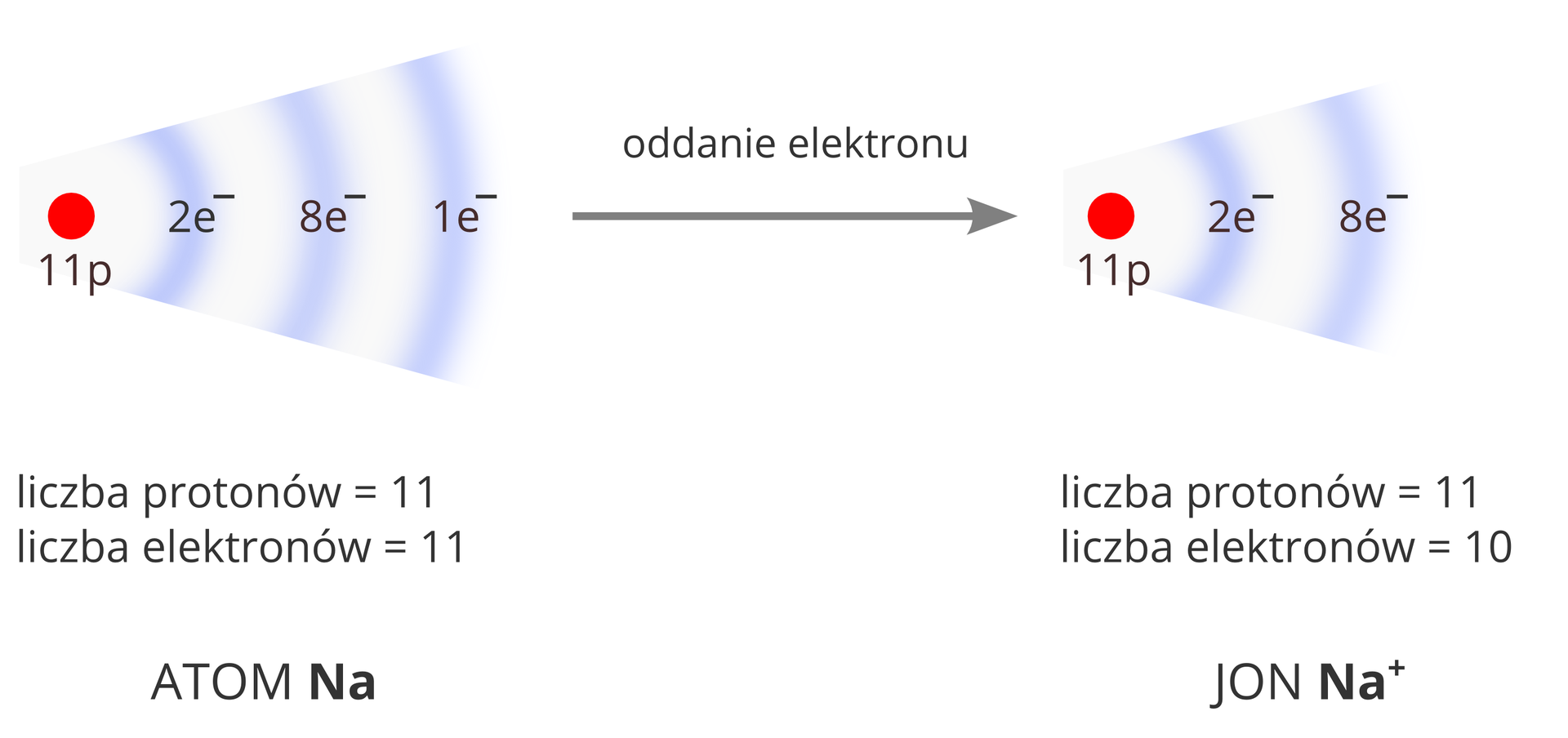
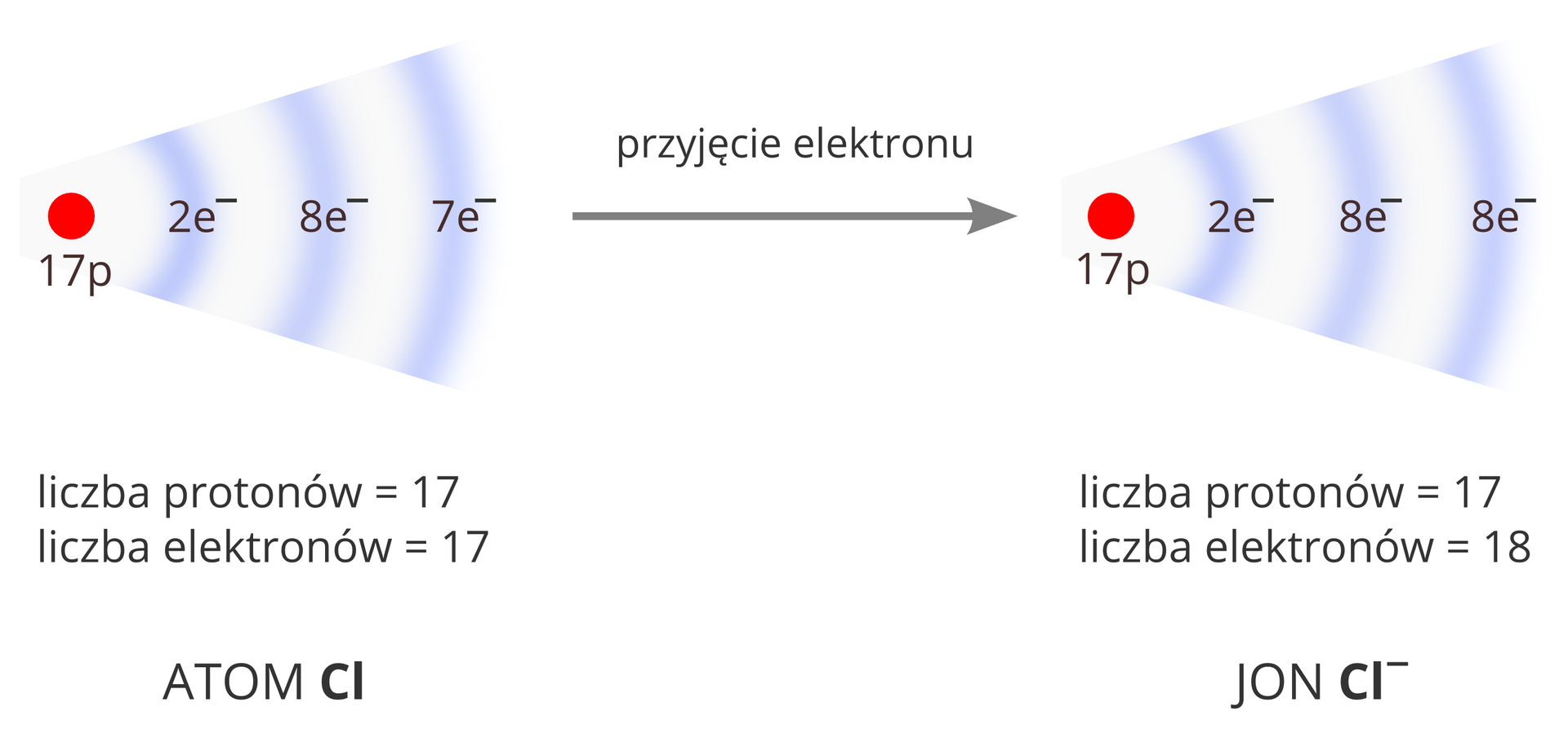
Jony ujemne powstają, gdy do atomu zostaną dostarczone elektrony, a jony dodatnie – gdy elektrony zostaną odłączone. Najłatwiej zmienić liczbę elektronów na powłoce, która znajduje się najdalej od jądra. Dlatego też w przeprowadzonych dotąd doświadczeniach i symulacjach przemieszczały się tylko ładunki ujemne.
Ładunki elektryczne, które przemieszczają się pomiędzy ciałami stałymi, to elektrony.
Jądro atomowe skandu zbudowane jest z 45 protonów i neutronów, a wokół niego w chmurze elektronowej znajduje się 21 elektronów. Ile i jakie cząstki należy dostarczyć lub odebrać, aby skand stał się jonem ujemnym?
- Odłączyć przynajmniej jeden elektron.
- Odłączyć przynajmniej jeden proton.
- Dostarczyć przynajmniej jeden elektron.
- Dostarczyć przynajmniej jeden proton.
Atom cynku jest zbudowany z: Możliwe odpowiedzi: 1. protonów, elektronów i neutronów., 2. protonów i elektronów, neutronów., 3. protonów, elektronów, neutronów.
Połącz w pary tak, aby otrzymane zdania były prawdziwe.
odpychają się., to najmniejsza niepodzielna porcja ładunku elektrycznego., przyciągają się., ma więcej protonów niż elektronów., ma więcej elektronów niż protonów.
| Ładunki różnoimienne | |
| Jon ujemny | |
| Ładunki jednoimienne | |
| Jon dodatni | |
| Ładunek elementarny |
Ładunek elementarny
Pod koniec wieku elektron opisywano jako pewną cząstkę. Tak scharakteryzował ją Hendrik Antoon Lorentz: „...zróbmy założenie, że w każdego rodzaju materii są obecne nadzwyczaj drobne cząsteczki, których jedna połowa posiada niezmiennie ładunki dodatnie, druga zaś tak samo ładunki ujemne...”. Owe drobniutkie cząstki, o których mowa, mają być najmniejsze z tych, którymi zajmują się nauki przyrodnicze, mniejsze od cząsteczek (molekuł) i atomów samych. Nadajmy cząsteczkom tym, zarówno ujemnym jak i dodatnim, wspólne miano „elektronów”, odróżniając je przymiotnikami „ujemny” i „dodatni”. Przypuśćmy dalej, że te elektryczne cząsteczki – elektrony – rozpowszechnione są we wszystkich ciałach, że żadna, nawet najmniejsza cząsteczka materii nie jest od nich wolna, że ilość ich w każdym ciele jest prawie niezliczona i że wreszcie, skoro jakieś ciało nie wykazuje objawów elektrycznych, posiada oba rodzaje elektronów w tej samej ilości. (cyt. za: A. K. Wróblewski, Historia fizyki, Wydawnictwo Naukowe PWN, Warszawa , str. ).
Z tej teorii można wyciągnąć wniosek, że ładunek elektryczny, jakim mogą być obdarzone różne ciała, ma naturę ziarnistą, jest bowiem wielokrotnością najmniejszego ładunku. Ładunek ten nazywany jest ładunkiem elementarnym. Kolejny wniosek jest następujący: ciała nienaelektryzowane mają po tyle samo ładunków dodatnich i ujemnych, a naładowane – więcej ładunków jednego znaku („” lub „”).
Składniki materii mające elementarne ładunki ujemne nazywamy obecnie elektronami. Wiemy również, że istnieją cząstki elementarne o ładunku dodatnim (ładunek ma taką samą wartość, jak ładunek elektronu, ale przeciwny znak). Są to protony – cząstki o masie znacznie większej, niż masa elektronu.
Oczywiście, ta hipoteza wymagała potwierdzenia doświadczalnego. Dokonał tego Robert Millikan. W latach udowodnił, że ładunek elektryczny ma strukturę ziarnistą, i wyznaczył wartość ładunku elementarnego. Obecnie przyjmujemy, że wynosi on .
Ładunek elektryczny to wielokrotność ładunku elementarnego:
;
gdzie: – ładunek elementarny.
Cząstka | Ładunek | Masa |
|---|---|---|
Elektron | ||
Proton | ||
Neutron |
Uzupełnij puste miejsca.
elektron, przeciwne, w elektronach, równe, neutron, w jądrze
Ładunki elektronu i protonu są ............................ co do wartości, a znaki ładunków są ............................. Z poznanych cząstek największą masę ma ............................, a najmniejszą masę – ............................. Można więc stwierdzić, że prawie cała masa atomu skupiona jest .............................
Nagroda Nobla za wyznaczenie ładunku elektronu.
Robert Millikan nie tylko wyznaczył ładunek elektronu, lecz także wyjaśnił wspólnie z Albertem Einsteinem tzw. zewnętrzny efekt fotoelektryczny (będzie o tym mowa na późniejszych etapach edukacji). W r. za swoje osiągnięcia otrzymał Nagrodę Nobla.
W latach wieku podczas badania promieniowania kosmicznego odkryto cząstki o masie równej masie elektronu, ale o ładunku dodatnim. Nazwano je pozytonami.
Siła Coulomba
Siła elektrostatyczna zależy od wielkości ładunków ciał, które na siebie oddziaływają oraz od ich odległości. Im większe są ładunki, tym większa jest ta siła. Gdy zwiększamy odległość między ładunkiami, siła elektrostatyczna maleje. Zależności te opisuje prawo Coulomba.
Siły wzajemnego oddziaływania dwóch ładunków punktowych i są wprost proporcjonalne do iloczynu tych ładunków, a odwrotnie proporcjonalne do kwadratu odległości między nimi. Oznacza to, że gdy odległość jest stała, to siła wzajemnego oddziaływania rośnie tyle razy ile razy wzrośnie każdy ładunek – gdy każdy z nich wzrośnie dwa razy, to siła wzrośnie razy. Gdy tylko jeden z nich wzrośnie np. tylko razy to siła wzajemnego oddziaływania wzrośnie razy. Przy stałej wartości ładunków siła maleje z kwadratem wzrostu odległości – np. dwukrotny wzrost odległości powoduje czterokrotne zmniejszenie wartości siły.
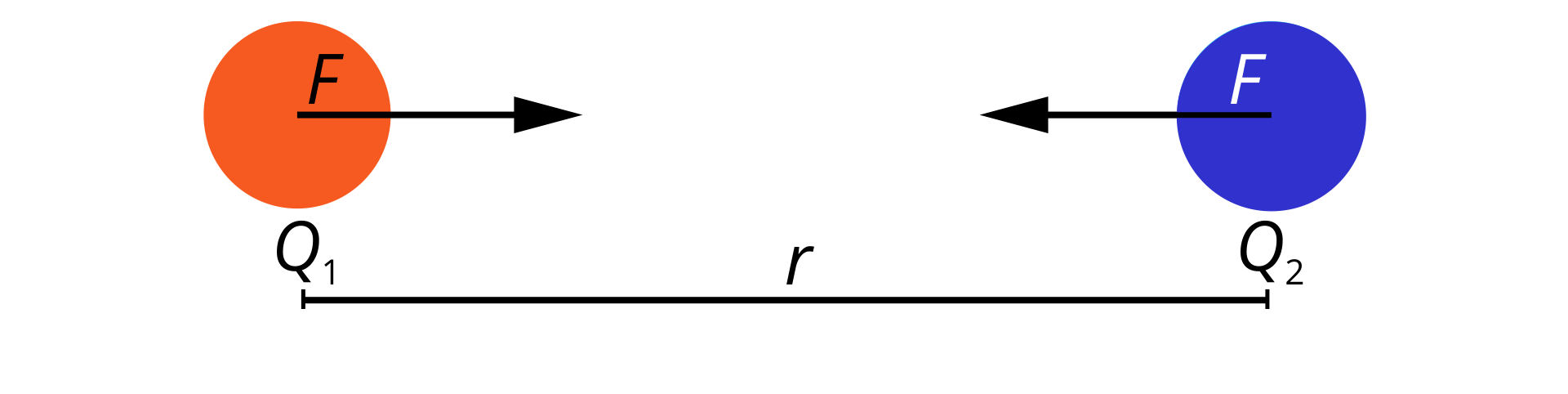
Tę zależność można zapisać jako:
gdzie:
– wartość siły,
– stała elektrostatyczna równa ,
, – punktowe ładunki elektryczne,
– odległość między punktowymi ładunkami elektrycznymi.
Za pomocą tego wzoru można obliczyć wielkość działającej siły elektrostatycznej.
naładowane ciała, które są małe w porównaniu z dzielącą je odległością.
Prawo Coulomba sprawdza się także w odniesieniu do ładunków umieszczonych na powierzchniach kulistych. Odległość mierzymy wówczas między środkami kul.
Siły elektrostatyczne z jakimi działają na siebie naelektryzowane ciała zależą od Możliwe odpowiedzi: 1. wielkości ładunków zgromadzonych na ciałach., 2. znaków ładunków zgromadzonych na ciałach., 3. rozmiarów ciał i ich masy., 4. odległości między ciałami.
Dokończ zdanie, wybierając właściwe odpowiedzi (więcej niż jedną). Siły elektrostatyczne z jakimi działają na siebie naelektryzowane ciała zależą od
- wielkości ładunków zgromadzonych na ciałach.
- znaków ładunków zgromadzonych na ciałach.
- rozmiarów ciał i ich masy.
- odległości między ciałami.
Zastanów się, jak zmiany wartości poszczególnych wielkości fizycznych wpływają na zmianę wielkości siły oddziaływania. Skorzystaj z poniższej aplikacji. Zbadaj, jak zmieni się wartość siły Coulomba, gdy nastąpi:
dwukrotne zwiększenie wartości jednego z ładunków bez zmiany odległości ciał,
dwukrotne zwiększenie wartości obu ładunków elektrycznych bez zmiany odległości ciał,
dwukrotne zwiększenie odległości między ciałami bez zmiany ich ładunków,
dwukrotne zmniejszenie odległości obu ciał bez zmiany ładunków,
dwukrotne zwiększenie odległości ciał z jednoczesnym dwukrotnym zwiększeniem wartości jednego z ładunków,
dwukrotne zwiększenie odległości ciał z jednoczesnym dwukrotnym zwiększeniem wartości obu ładunków.
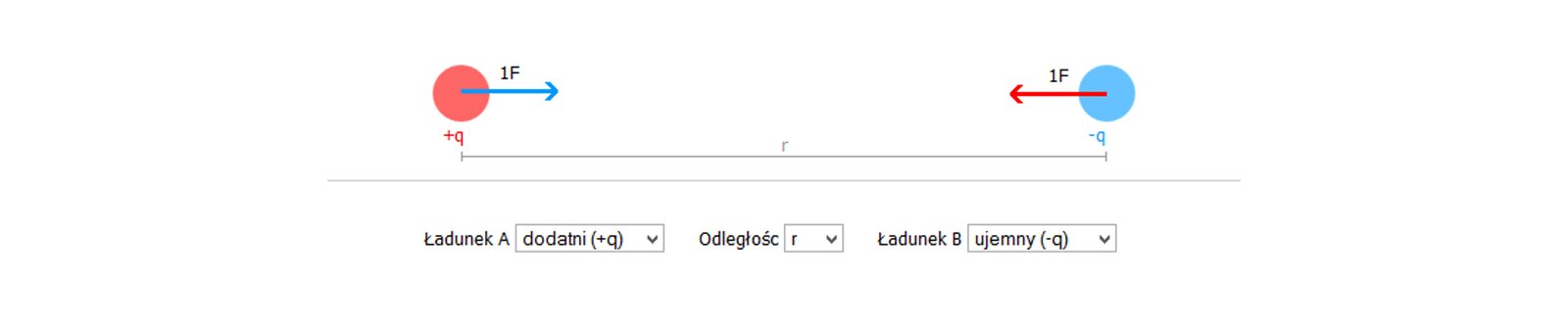
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pqvz8S0S5
Zastanów się, jak zmiany wartości poszczególnych wielkości fizycznych wpływają na zmianę wielkości siły oddziaływania. Jak będzie zmieniała się siła przy zmianach wartości (i znaków, w przypadku ładunków) składników wzoru na siłę? Zbadaj, jak zmieni się wartość siły Coulomba gdy nastąpi:
dwukrotne zwiększenie wartości jednego z ładunków bez zmiany odległości ciał,
dwukrotne zwiększenie wartości obu ładunków elektrycznych bez zmiany odległości ciał,
dwukrotne zwiększenie odległości między ciałami bez zmiany ich ładunków,
dwukrotne zmniejszenie odległości obu ciał bez zmiany ładunków,
dwukrotne zwiększenie odległości ciał z jednoczesnym dwukrotnym zwiększeniem wartości jednego z ładunków,
dwukrotne zwiększenie odległości ciał z jednoczesnym dwukrotnym zwiększeniem wartości obu ładunków.
Siła Coulomba zależy zarówno od odległości między ładunkami, jak i od ich wartości. Gdy odległość rośnie, to siła maleje, a gdy odległość maleje, siła rośnie. Wzrost lub spadek wielkości siły oddziaływania elektrostatycznego może również spowodować zmiana wartości ładunku elektrycznego zgromadzonego na ciałach. Im jest on większy, tym większa jest siła i odwrotnie: gdy ładunek elektryczny maleje, maleje również siła.
Podsumowanie
Ładunki jednoimienne się odpychają, a różnoimienne – przyciągają.
Wartość siły elektrycznej między dwoma naelektryzowanymi ciałami zależy zarówno od wartości ładunku zgromadzonego na ciałach, jak i od odległości między nimi.
Wartość ładunku protonu odpowiada ładunkowi elementarnemu. Ładunek elektronu ma taką samą wartość jak ładunek protonu, ale przeciwny znak (ujemny).
Wielkość ładunku elementarnego wynosi .
Każdy atom jest obojętny elektrycznie. Jeśli do atomu zostaną dostarczone elektrony, to staje się on jonem ujemnym, a jeśli elektrony zostaną odłączone – jonem dodatnim.
Na podstawie dowolnego źródła, np. internetu, postaraj się odnaleźć informacje na temat zdarzeń, w których istotną rolę odegrał nagromadzony ładunek elektrostatyczny.
Słownik
najmniejsza cząstka pierwiastka. Każdy atom jest obojętny elektrycznie.

Charles Augustin de Coulomb
[szarl ogiustę dy kulą] Kapitan armii francuskiej, przyrodnik i matematyk. Ukończył studia w Wojskowej Szkole Inżynierii (franc. École du Génie). W latach kierował budową Fortu Bourbon na Martynice (Indie Zachodnie). Po powrocie do Francji poświęcił się pracy naukowej. W roku został uhonorowany tytułem członka Francuskiej Akademii Nauk. Był doskonałym eksperymentatorem. Do jego największych osiągnięć naukowych należą pomiar siły oddziaływań między ładunkami elektrycznymi (przeprowadzony przy użyciu tzw. wagi skręceń) oraz prace dotyczące sił tarcia i oporu w płynach.
atom, który ma nadmiar lub niedobór elektronów.
atom, w którym liczba protonów przewyższa liczbę elektronów.
atom, w którym liczba elektronów jest większa od liczby protonów.
stała fizyczna o wartości , odpowiadająca ładunkowi elektrycznemu protonu.
jednostka ładunku elektrycznego w układzie SI.
podwielokrotność kulomba, równa .
podwielokrotność kulomba, równa .
substancja chemiczna składająca się z atomów, które mają taką samą liczbę atomową.
liczba protonów w jądrze atomu; oznaczana literą .
patrz: liczba atomowa.
liczba protonów i neutronów (nukleonów) w jądrze atomowym; oznaczana literą .
składnik jądra atomowego; ładunek protonu odpowiada wielkości ładunku elementarnego. Proton to główny składnik promieniowania kosmicznego.
obojętny elektrycznie składnik jądra atomowego.
cząstka elementarna, której ładunek elektryczny odpowiada wielkości ładunku elementarnego o znaku ujemnym. Powłoki elektronowe w atomach są tworzone przez elektrony. Ich ruch jest ściśle związany ze zjawiskiem przepływu prądu elektrycznego.
tabela zawierająca wszystkie znane dotąd pierwiastki chemiczne, uporządkowane według ich rosnącej liczby atomowej. Pierwotną formą układu okresowego była tzw. tablica Mendelejewa, której nazwa pochodzi od nazwiska wybitnego rosyjskiego chemika Dymitra Mendelejewa. Jej obecny wygląd zawdzięczamy Nielsowi Bohrowi – duńskiemu fizykowi, laureatowi Nagrody Nobla.
Zadania
Dwukrotne zwiększenie wartości jednego z ładunków powoduje, że wartość siły Coulomba Możliwe odpowiedzi: 1. wzrośnie dwukrotnie., 2. zmaleje dwukrotnie., 3. pozostanie taka sama., 4. zmaleje jak kwadrat odwrotności., 5. wzrośnie jak kwadrat odwrotności.
Dwukrotne zwiększenie wartości jednego z ładunków powoduje, że wartość siły Coulomba
- wzrośnie dwukrotnie.
- zmaleje dwukrotnie.
Dwukrotne zwiększenie wartości obu ładunków elektrycznych powoduje, że wartość siły Coulomba Możliwe odpowiedzi: 1. zmaleje dwukrotnie., 2. wzrośnie dwukrotnie., 3. zmaleje czterokrotnie., 4. wzrośnie czterokrotnie.
Dwukrotne zwiększenie wartości obu ładunków elektrycznych powoduje, że wartość siły Coulomba
- zmaleje dwukrotnie.
- wzrośnie dwukrotnie.
- zmaleje czterokrotnie.
- wzrośnie czterokrotnie.
Opierając się na wynikach symulacji, można stwierdzić, że wartość sił wzajemnego oddziaływania Możliwe odpowiedzi: 1. jest wprost proporcjonalna do iloczynu wielkości ładunków., 2. nie zależy od wielkości ładunków., 3. zależy tylko od wielkości jednego z ładunków.
Opierając się na wynikach symulacji, można stwierdzić, że wartość sił wzajemnego oddziaływania
- jest wprost proporcjonalna do iloczynu wielkości ładunków.
- nie zależy od wielkości ładunków.
- zależy tylko od wielkości jednego z ładunków.
Dwukrotne zwiększenie odległości między ciałami bez zmiany ładunków powoduje, że wartość siły Możliwe odpowiedzi: 1. zmaleje dwukrotnie., 2. wzrośnie dwukrotnie., 3. wzrośnie czterokrotnie., 4. zmaleje czterokrotnie.
Dwukrotne zwiększenie odległości między ciałami bez zmiany ładunków powoduje, że wartość siły
- zmaleje dwukrotnie.
- wzrośnie dwukrotnie.
- wzrośnie czterokrotnie.
- zmaleje czterokrotnie.
Na podstawie symulacji i odpowiedzi na poprzednie pytanie, można stwierdzić, że wartość siły jest Możliwe odpowiedzi: 1. odwrotnie proporcjonalna do odległości między naładowanymi ciałami., 2. odwrotnie proporcjonalna do kwadratu odległości między naładowanymi ciałami., 3. wprost proporcjonalna do odległości między naładowanymi ciałami., 4. wprost proporcjonalna do kwadratu odległości między naładowanymi ciałami.
Na podstawie symulacji i odpowiedzi na poprzednie pytanie, można stwierdzić, że wartość siły jest
- odwrotnie proporcjonalna do odległości między naładowanymi ciałami.
- odwrotnie proporcjonalna do kwadratu odległości między naładowanymi ciałami.
- wprost proporcjonalna do odległości między naładowanymi ciałami.
- wprost proporcjonalna do kwadratu odległości między naładowanymi ciałami.
Na podstawie analizy wzoru na siłę Coulomba i odpowiedzi na poprzednie pytanie, można stwierdzić, że wartość siły jest Możliwe odpowiedzi: 1. odwrotnie proporcjonalna do odległości między naładowanymi ciałami., 2. odwrotnie proporcjonalna do kwadratu odległości między naładowanymi ciałami., 3. wprost proporcjonalna do odległości między naładowanymi ciałami., 4. wprost proporcjonalna do kwadratu odległości między naładowanymi ciałami.
Wybierz prawidłowe stwierdzenia dotyczące oddziaływań między kulkami. Dwie kulki (o rozmiarach zbliżonych do piłki ping-pongowej) naelektryzowano tak, że na pierwszej zebrał się ładunek równy +3 μC, a na drugiej -5 μC. Następnie umieszczono je w odległości 5 cm.
- Kulki przyciągają się siłami o tej samej wartości.
- Kulki przyciągają się siłami o tej samej wartości, ponieważ mają zbliżone rozmiary i kształt.
- Pierwsza kulka mocniej przyciąga drugą, ponieważ jej ładunek jest dodatni.
- Druga kulka mocniej przyciąga pierwszą, ponieważ jej ładunek jest większy.
- Zwiększenie odległości do 10 cm spowoduje, że siła przyciągania będzie większa dwukrotnie.
- Dowolne zmniejszenie odległości spowoduje, że siła przyciągania wzrośnie.
- Zwiększenie odległości do 10 cm spowoduje, że siła przyciągania będzie mniejsza czterokrotnie.
Jeśli do jednej kulki dostarczymy ładunek, podwajając go, to wartość siły 1. wzrośnie, 2. , 3. , 4. wzrośnie, 5. zmaleje i będzie równa 1. wzrośnie, 2. , 3. , 4. wzrośnie, 5. zmaleje .
Uzupełnij puste miejsca.
Dwie naelektryzowane kulki przyciągają się wzajemnie siłami 36 mN. Jeśli odległość między nimi zwiększymy dwukrotnie, to wartość każdej siły .............. i będzie równa ............ mN.
Jeśli do jednej kulki dostarczymy ładunek, podwajając go, to wartość każdej z sił .................. i będzie równa ............ mN.