2. Odcinki prostopadłe i równoległe
Na co dzień bardzo często posługujemy się nazwami kierunków. Mówimy: idź prosto, skręć w lewo, spójrz w górę, zobacz, co się dzieje na dole. Im bardziej precyzyjnie wyrażamy nasze myśli, tym lepiej jesteśmy rozumiani i tym mniej nieprzewidzianych przeszkód do pokonania staje na naszej drodze. Matematyka uczy nas między innymi określania kierunków oraz precyzyjnego wysławiania się.
Niektóre ulice miast, krawędzie regałów, ramy obrazów są położone względem siebie prostopadle. Odejście od zasad prostopadłości w typowych sytuacjach może przyprawiać o zawrót głowy. Przykładem może być „krzywy domek” w Sopocie pokazany na poniższej animacji.

Film dostępny pod adresem /preview/resource/RhqiTEdxbsybD
Animacja przedstawia "Krzywy domek", który znajduje się w Sopocie.
Prostopadłość i równoległość odcinków i prostych
Analizując przykłady zawarte w tym materiale, poznasz wzajemne położenie prostych na płaszczyźnie. Rozwiązując ćwiczenia, wykorzystasz zdobytą wiedzę w zadaniach konstrukcyjnych i tekstowych.

Film dostępny pod adresem /preview/resource/R1T6kkUmzbPbj
Animacja przedstawia, które proste możemy nazywać równoległymi, a które nazywamy przecinającymi się.
Spróbuj opisać wzajemne położenie prostych przedstawionych na rysunku.

Przygotuj kartkę papieru. Zegnij ją w dowolnym miejscu. Następnie zegnij ją drugi raz, tak jak na rysunku i animacji.


Film dostępny pod adresem /preview/resource/RFVZ5y2yFENTY
Animacja przedstawia w jaki sposób możemy uzyskać kąt prosty składając kartkę papieru.
Zaznacz kolorem róg kartki.
Przyłóż zaznaczony róg do pomarańczowych prostych widocznych na rysunku zamieszczonym nad Poleceniem 1 tak, aby jedna z linii układała się wzdłuż jednego brzegu, a druga wzdłuż drugiego brzegu pomalowanego rogu kartki. W ilu miejscach możesz przyłożyć kartkę? W jednym? W dwóch? W trzech? A może w czterech?
Rysując proste prostopadłe, często posługujemy się ekierką.

Zapoznaj się z animacją obrazującą rysowanie prostych prostopadłych.

Film dostępny pod adresem /preview/resource/RNyuElAZB310Y
Animacja przedstawia w jaki sposób możemy narysować proste prostopadłe.
Uruchom aplet i postępuj zgodnie z zawartą tam instrukcją.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDhaHEpLy
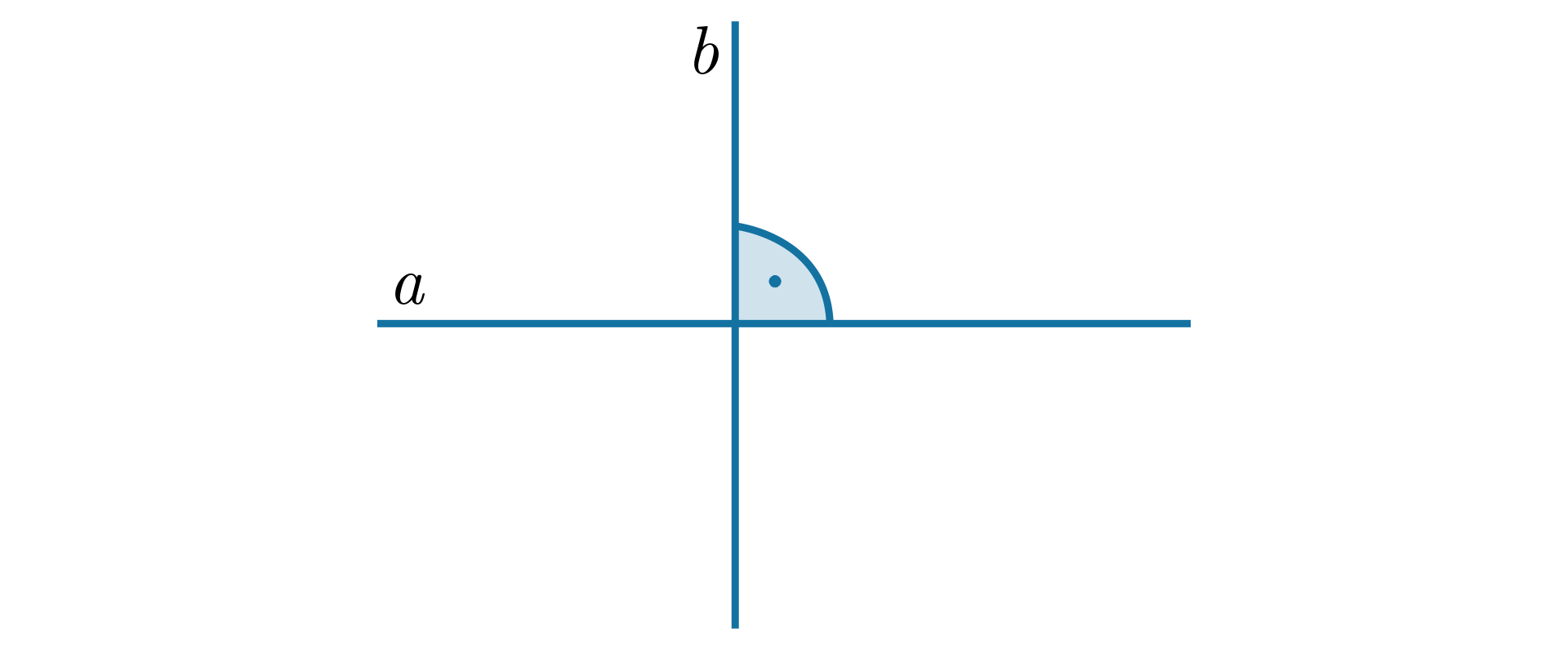
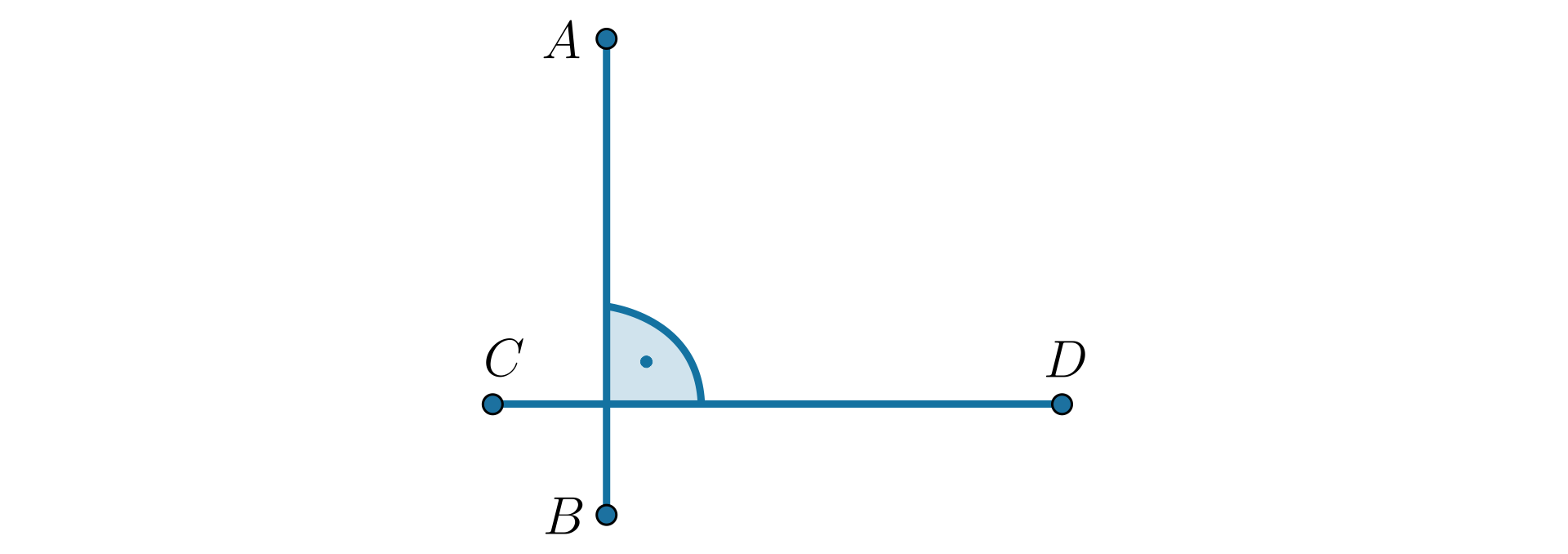
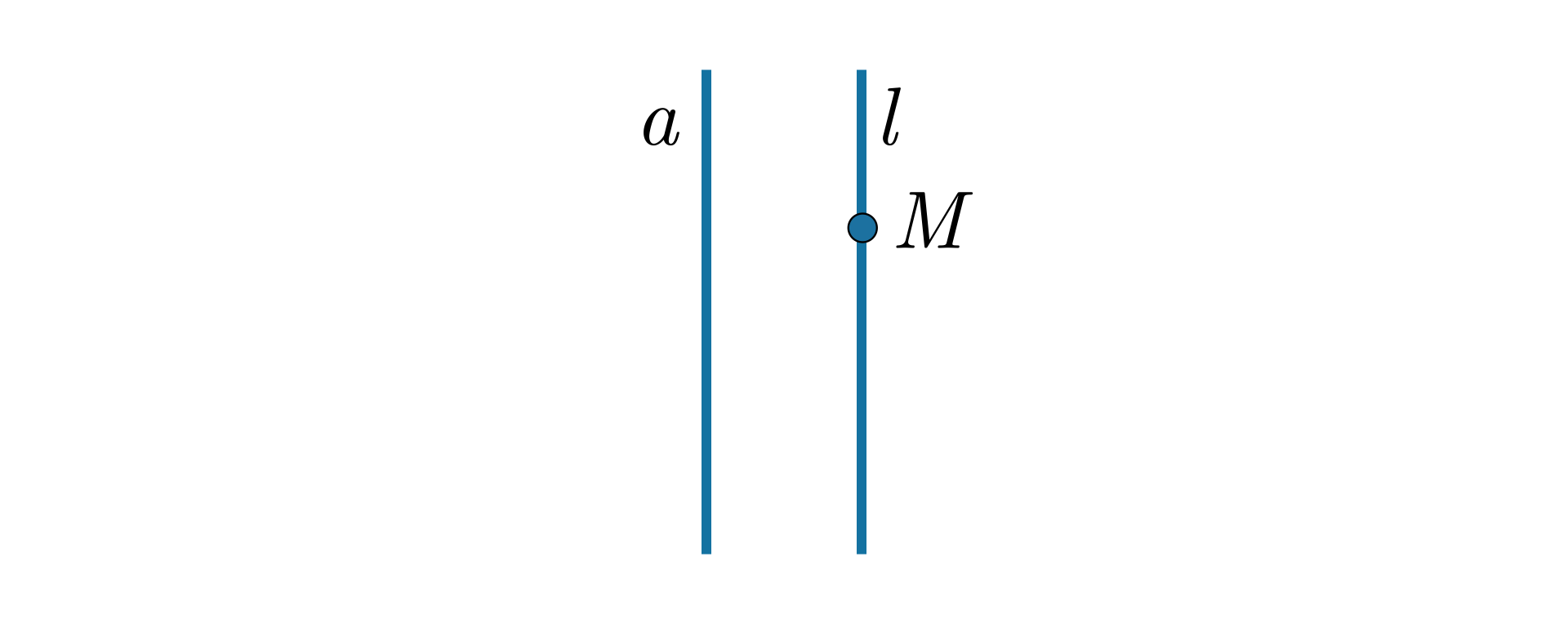
Na rysunku prosta jest prostopadła do prostej .
Możemy zapisać:

O odcinkach leżących na prostych prostopadłych mówimy także, że są prostopadłe.

Zapoznaj się z animacją obrazującą rysowanie prostych równoległych.
Film dostępny pod adresem /preview/resource/RpCpMSqWhJvcI
Animacja przedstawia w jaki sposób możemy narysować proste równoległe.
Zapoznaj się z poniższym apletem.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDhaHEpLy
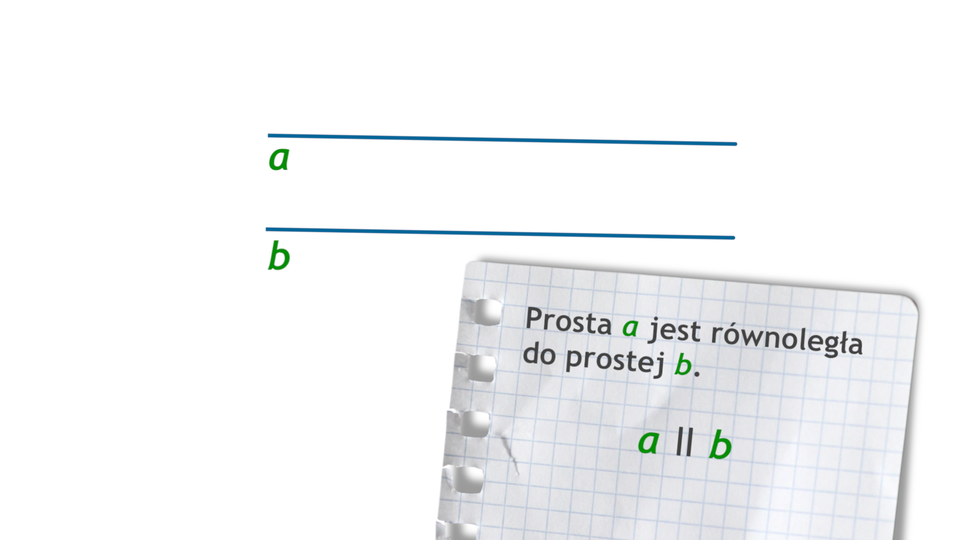
Na rysunku prosta jest równoległa do prostej .
Możemy to zapisać symbolicznie: .

O odcinkach leżących na prostych równoległych także mówimy, że są równoległe.

Odległość punktu od prostej
Co nazywamy odległością punktu od prostej?
Jak konstrukcyjnie wyznaczyć tę odległość?
Jak sprawdzić, czy narysowany odcinek określa odległość danego punktu od danej prostej?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDhaHEpLy
Odległość punktu od prostej to długość najkrótszego odcinka łączącego ten punkt z prostą.

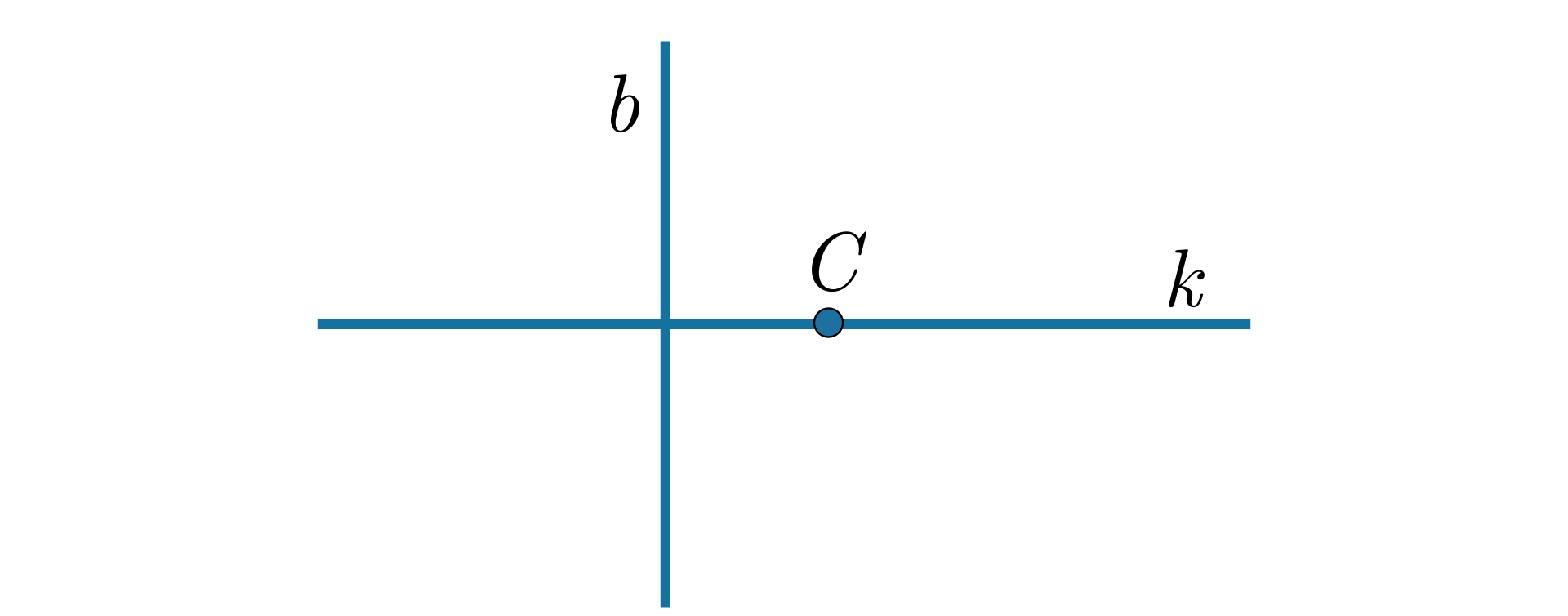
Odległość punktu od prostej to długość odcinka , prostopadłego do prostej .
Odległość dwóch prostych równoległych to długość najkrótszego odcinka łączącego te proste. Odcinek ten jest prostopadły do obu tych prostych.

Odległość prostych i to długość odcinka .
Narysuj dwie proste prostopadłe.
Narysuj dwa odcinki prostopadłe, które się przecinają. Oznacz ich końce literami. Zapisz symbolami, że są one prostopadłe.
Narysuj dowolną prostą i dowolny punkt tak, aby
punkt leżał na prostej ,
punkt leżał poza prostą .
Narysuj prostą prostopadłą do prostej przechodzącą przez punkt .
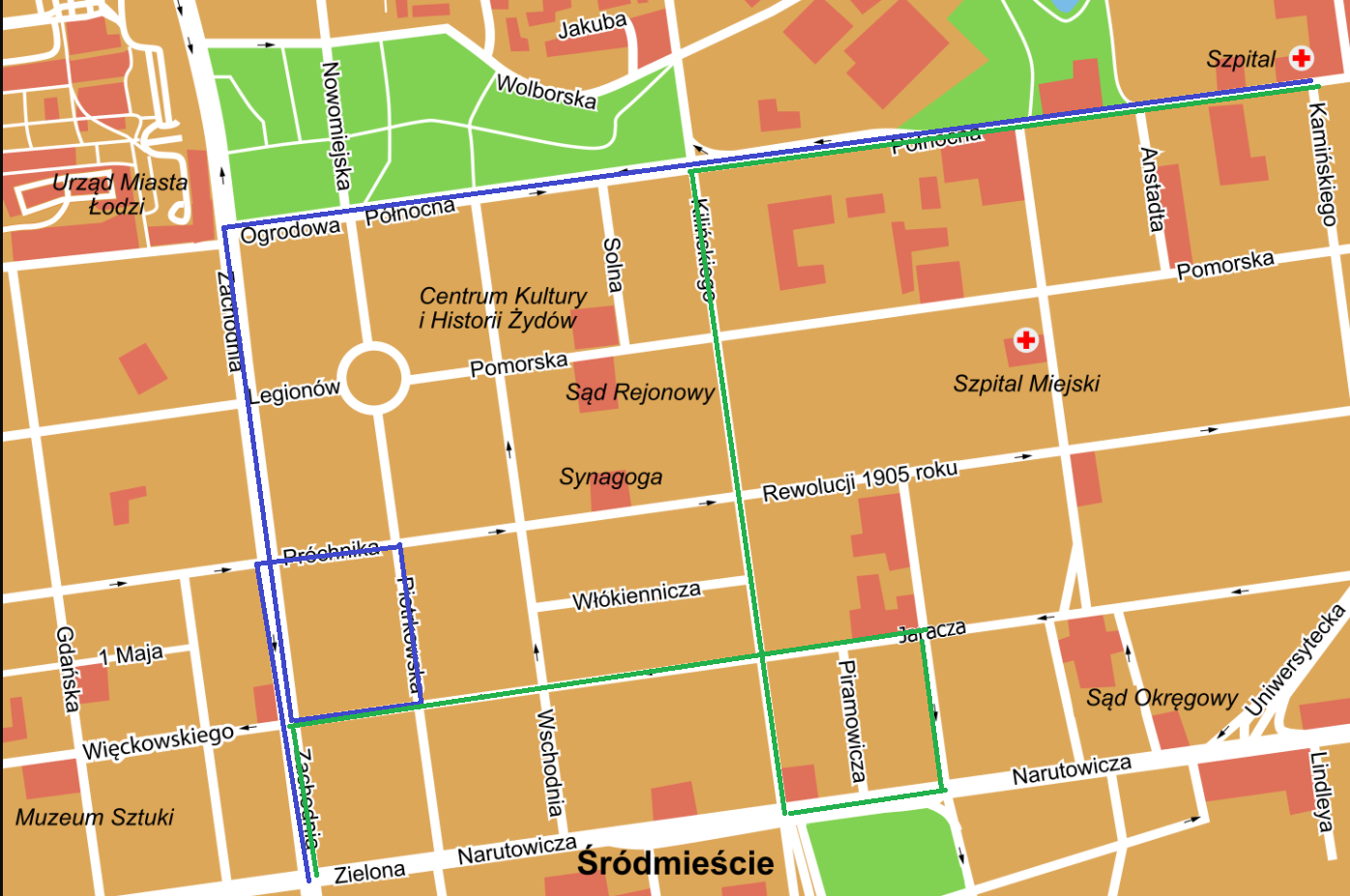
Zapoznaj się z poniższym planem miasta.
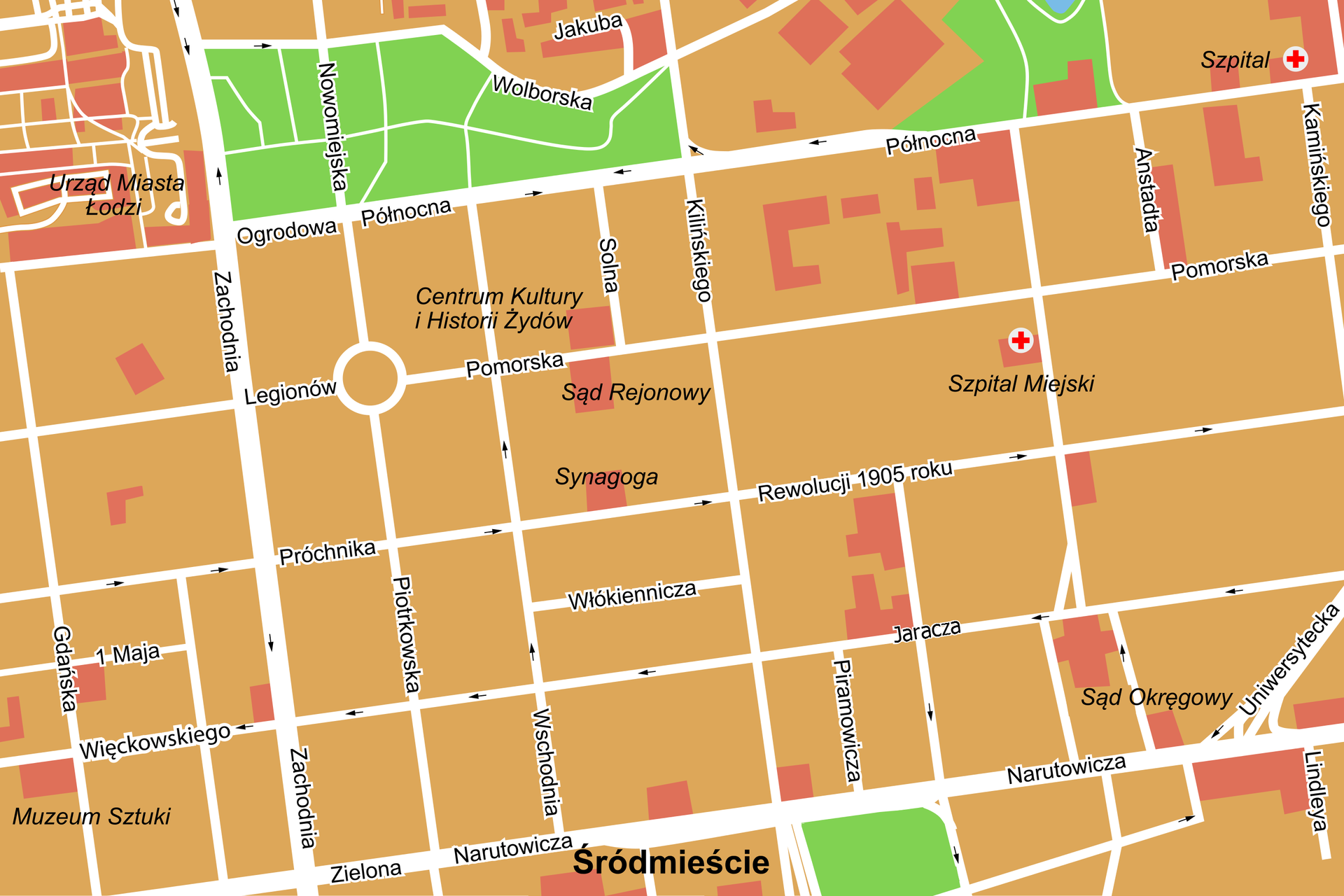
1. Rewolucji, 2. Więckowskiego, 3. Pomorską, 4. Północna, 5. Kilińskiego, 6. Piotrkowska.
Korzystając z mapy, zaplanuj dwie trasy spaceru od skrzyżowania ulic Północnej i Kamińskiego do skrzyżowania Zachodniej i Zielonej, tak aby po drodze trzeba było wykonać dokładnie pięć prostopadłych skrętów wyłącznie w lewo. W którą stronę trzeba będzie skręcać, gdy zechcemy spacerować tą samą trasą w przeciwną stronę?

Narysuj dwie proste równoległe.
Narysuj prostą i punkt , który nie leży na tej prostej. Narysuj prostą równoległą do prostej , przechodzącą przez punkt .
Oto fragment planu Gdańska.

Zaznacz wszystkie prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. Ulica Zuchów jest prostopadła do ulicy Bluszczowej., 2. Ulica Pasieczna jest równoległa do ulicy Sierpowej., 3. Ulica Modra jest równoległa do ulicy Łanowej., 4. Ulica Łanowa jest równoległa do ulicy Śnieżki., 5. Ulica Gęsia jest równoległa do ulicy Niezapominajek., 6. Ulica Żurawia jest równoległa do ulicy Jaśminowej.
- Ulica Zuchów jest prostopadła do ulicy Bluszczowej.
- Ulica Pasieczna jest równoległa do ulicy Sierpowej.
- Ulica Modra jest równoległa do ulicy Łanowej.
- Ulica Łanowa jest równoległa do ulicy Śnieżki.
- Ulica Gęsia jest równoległa do ulicy Niezapominajek.
- Ulica Żurawia jest równoległa do ulicy Jaśminowej.
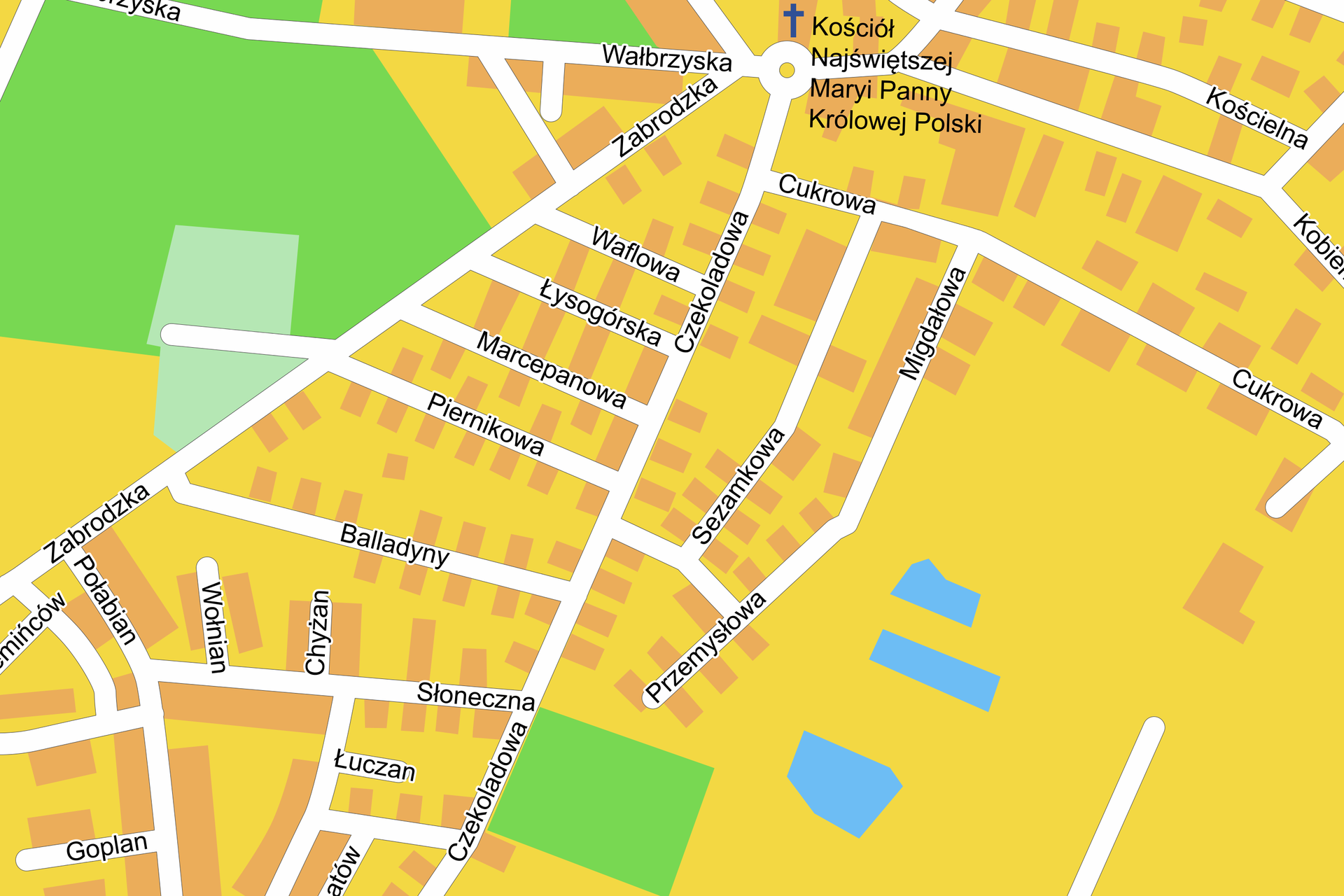
Poniżej znajduje się plan jednej z dzielnic Wrocławia.
Ulice Zabrodzka i Czekoladowa nie są do siebie równoległe. Słoneczna i Piernikowa także nie są równoległe. Sprawdź to.
Ulice Piernikowa i Marcepanowa są do siebie równoległe. Podobnie Marcepanowa i Łysogórska oraz Łysogórska i Waflowa. Które z pozostałych ulic na planie są do siebie równoległe?
Żadna z ulic wymienionych w podpunkcie b) tego zadania nie jest prostopadła do ulicy Zabrodzkiej. Do jakiej ulicy jest prostopadła każda z tych ulic?
Jakie jeszcze dwie inne ulice na tym planie są do siebie prostopadłe?
Kiedy spojrzymy na fragment torów kolejowych, zauważymy, że szyny są do siebie równoległe. Jak to się dzieje, że jadąc pociągiem dłuższy czas nie zawsze poruszamy się po linii prostej? Spróbuj znaleźć odpowiedź na to pytanie.

Zdjęcie zamieszczone poniżej zrobiono z okna ostatniego wagonu jadącego pociągu. Dlaczego równoległe linie szyn kolejowych nie wydają się na tym zdjęciu równoległe?

Wypisz wszystkie znalezione na rysunku pary prostych:
równoległych,
prostopadłych,
przecinających się i nieprostopadłych.

Dany jest kwadrat z poprowadzonymi przekątnymi i . Wypisz wszystkie pary boków:
równoległych,
prostopadłych.
Narysuj dwie proste równoległe, używając linijki i ekierki.
Opisz, jak przy użyciu ekierki i linijki skonstruować proste równoległe.
Narysuj prostą i punkt nieleżący na prostej . Następnie narysuj prostą równoległą do prostej i przechodzącą przez punkt .
Dana jest prosta i punkt nieleżący na prostej . Opisz konstrukcję prostej równoległej do prostej i przechodzącej przez punkt .
Narysuj dwie proste prostopadłe, używając linijki i ekierki.
Opisz jak przy użyciu ekierki i linijki narysować dwie proste prostopadłe.
Narysuj prostą i punkt nieleżący na prostej . Następnie narysuj prostą prostopadłą do prostej i przechodzącą przez punkt .
Dana jest prosta i punkt nieleżący na prostej . Opisz konstrukcję prostej prostopadłej do prostej i przechodzącej przez punkt .
Uzupełnij zapisy, przeciągając w luki odpowiednie symbole lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
Zapoznaj się z poniższą ilustracją.

Co powiesz o odległości tych punktów od prostej ?
Zapoznaj się z poniższą grafiką, która przedstawia pewien dwunastokąt.

Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.