2. Zastosowanie wielkości wprost proporcjonalnych

RlFmm8NxmTwdS

Do właściwej interpretacji i wyznaczenia rozwiązań problemów matematycznych używamy różnych modeli matematycznych. Jednym z takich modeli są wielkości wprost proporcjonalne, które spotykamy na przykład w przepisach kulinarnych. Poniżej przedstawiono przepis na pieczenie sernika. Zastanów się, ile składników potrzeba, jeżeli chcemy upiec $3$ takie serniki. Jak zmieni się liczba i masa poszczególnych składników, gdy chcemy upiec sernik o masie $2$ razy mniejszej?

RYQQCBRXKUrJD

Na ilustracji znajduje się zdjęcie sernika oraz lista produktów potrzebna do jego wykonania. Na liście składników potrzebnych do masy serowej znajduje się: 1 kilogram sera, 32 dekagramy drobnego cukru do wypieków, 8 jajek, 16 dekagramów miękkiego masła, 4 łyżki kaszy manny, 30 gram budyniu śmietankowego bez cukru, 2 łyżeczki cukru waniliowego, dwie trzecie szklanki śmietany kremówki (30%), pół łyżeczki aromatu pomarańczowego, 10 dekagramów kandyzowanej skórki pomarańczowej. Na liście składników potrzebnych do polewy czekoladowej znajduje się: 50 mililitrów śmietany kremówki 30% oraz 5 dekagramów gorzkiej czekolady. — Źródło: Grafika na podstawie: Pexels.com, licencja: CC BY 3.0.

W życiu codziennym spotykamy się z sytuacjami, gdy iloraz pewnych wielkości jest stały np.

iloraz odległości w jakiej uderza piorun do czasu, po jakim usłyszymy grzmot,
iloraz odległości w terenie do odpowiadającej jej odległości na mapie,
iloraz wartości zakupionego towaru do jego masy.

R5XWnJw0gzbE71

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

wielkości wprost proporcjonalne

Definicja: wielkości wprost proporcjonalne

Dane są dwie dodatnie wielkości. Mówimy, że te wielkości są wprost proporcjonalne, jeżeli iloraz odpowiadających sobie wartości tych wielkości jest stały.

W przypadku wielkości wprost proporcjonalnych, wzrost lub zmniejszenie jednej wielkości, powoduje wzrost lub odpowiednio zmniejszenie drugiej wielkości tyle samo razy.

Wielkościami wprost proporcjonalnymi są na przykład:

długość boku trójkąta równobocznego i jego obwód,
waga jabłek i koszt ich zakupu,
rzeczywista odległość w terenie oraz odpowiadająca jej odległość na mapie.

Do wyznaczenia zależności pomiędzy wielkościami wprost proporcjonalnymi używa się proporcjiproporcjaproporcji.

Jeżeli wprowadzimy następujące oznaczenia:

a : b

– iloraz liczb

a

b

, gdzie

b \neq 0

c : d

– iloraz liczb

c

d

, gdzie

d \neq 0

to równość dwóch ilorazów $a : b = c : d$ nazywa się proporcjąproporcjaproporcją.

Liczby $a$ i $d$ nazywamy wyrazami skrajnymi, a liczby $b$ i $c$ wyrazami środkowymi.

R1Qz0mY70WycT1

Zapis równości. Lewa strona równania - ułamek: a dzielone przez b. Prawa strona równania - ułamek c dzielone przez d. Litery a, d są to wyrazy skrajne. Litery b, c są to wyrazy środkowe. Iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych. a razy d = b razy c. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wówczas mówimy, że iloraz wyrazów skrajnych jest równy ilorazowi wyrazów środkowych.

Ponieważ równanie $\frac{a}{b} = \frac{c}{d}$ jest równoważne równaniu $a \cdot d = b \cdot c$ , zatem wykorzystamy ten zapis do rozwiązywania problemów matematycznych, w których występują wielkości wprost proporcjonalne.

Przykład 1

W tabeli przedstawiono wielkości $x$ i $y$ , które są wprost proporcjonalne. Wyznaczymy wartości liczb $k$ , $l$ oraz $m$ .

$x$	$y$
$3$	$5$
$k$	$23$
$12$	$l$
$m$	$12$

$\frac{3}{5} = \frac{k}{23}$ , czyli $5 k = 69$ , zatem $k = 13, 8$

$\frac{3}{5} = \frac{12}{l}$ , czyli $3 l = 60$ , zatem $l = 20$

$\frac{3}{5} = \frac{m}{12}$ , czyli $5 m = 36$ , zatem $m = 7, 2$

Przykład 2

Wiadomo, że $24$ ziarenka grochu ważą $6 g$ . Obliczymy, ile waży $20$ ziarenek grochu.

Rozwiązanie:

Jeżeli przez $x$ oznaczymy masę dwudziestu ziarenek grochu, to do wyznaczenia wartości $x$ rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{6}{24} = \frac{x}{20}$ , zatem $x = 5$ .

Odpowiedź:
$20$ ziarenek grochu ma masę $5 g$ .

Przykład 3

Wiadomo, że wielkości $a$ i $b$ zapisane w tabeli są wprost proporcjonalne. Obliczymy wartość $x$ .

$a$	$b$
$5 x - 2$	$4$
$- 2 x + 5$	$3$

Rozwiązanie:

Układamy i rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{5 x - 2}{4} = \frac{- 2 x + 5}{3}$

$3 \cdot (5 x - 2) = 4 \cdot (- 2 x + 5)$

$15 x - 6 = - 8 x + 20$

$23 x = 26$

Wobec tego $x = \frac{26}{23}$

Przykład 4

Na wycieczkę pojechało $56$ uczniów. Stosunek liczby dziewcząt do liczby chłopców jest równy $5 : 9$ . Wyznaczymy liczbę dziewcząt i liczbę chłopców biorących udział w wycieczce.

Rozwiązanie:

Niech $x$ będzie liczbą naturalną. Jeżeli przez $x$ oznaczymy liczbę dziewcząt w tej szkole, to liczba chłopców wynosi $56 - x$ oraz $0 < x < 56$ .

Układamy i rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{x}{56 - x} = \frac{5}{9}$ .

Zatem $9 \cdot x = 5 \cdot (56 - x)$ , czyli

$x = 20$ ,

$56 - x = 36$ .

Odpowiedź:
Liczba dziewcząt biorących udział w wycieczce wynosiła $20$ , a chłopców $36$ .

Przykład 5

Samochód pokonał trasę $280 km$ w ciągu $3, 5 h$ . Obliczymy, jakiej długości trasę pokonałby ten samochód w ciągu $6$ godzin, gdyby utrzymał tę samą średnią prędkość.

Rozwiązanie:

Jeżeli przez $x$ oznaczymy długość trasy jaką samochód pokona w ciągu $6 h$ , to do jej wyznaczenia rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{280}{3, 5} = \frac{x}{6}$ , zatem $6 \cdot 280 = 3, 5 \cdot x$ , czyli $x = 480$ .

Odpowiedź:
Przy tej samej średniej prędkości, samochód w ciągu $6 h$ pokonałby trasę długości $480 km$ .

Przykład 6

Listewkę podzielono na dwa mniejsze kawałki, których stosunek długości wynosi $4 : 9$ . Wyznaczymy, jaka jest długość każdej części listewki, jeżeli mniejsza część jest o $15 c m$ krótsza od większej części.

Rozwiązanie:

Wykonajmy rysunek pomocniczy do zadania i wprowadźmy następujące oznaczenia:

RVErIA54EC2qV

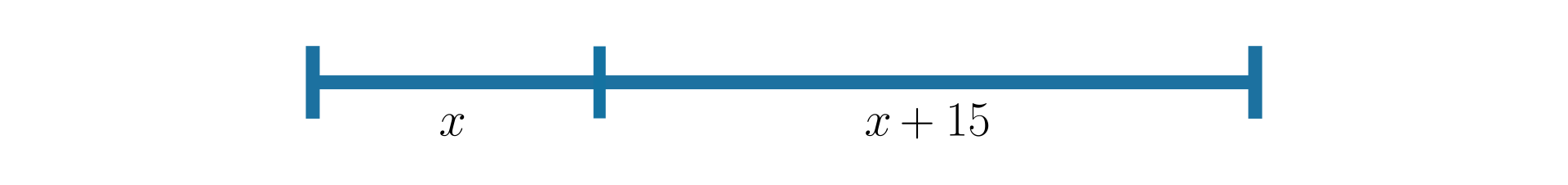
Na rysunku znajduje się odcinek podzielony na dwie części. Pierwsza, krótsza część odcinka ma długość x, a druga, dłuższa część odcinka ma długość x + piętnaście. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$x c m$ – długość krótszej części listewki,

$(x + 15) c m$ – długość dłuższej części listewki,

Układamy i rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{4}{9} = \frac{x}{x + 15}$ , zatem $9 \cdot x = 4 \cdot (x + 15)$ .

Po rozwiązaniu równania otrzymujemy, że $x = 12$ .

Odpowiedź:
Krótsza część listewki ma długość $12 c m$ , a dłuższa $27 c m$ .

Przykład 7

Wiadomo, że wielkości występujące po obu stronach równania są wprost proporcjonalne. Wyznaczymy rozwiązania tych równań.

$\frac{24}{x + 3} = \frac{18}{2 x - 1}$ ,
$\frac{3 x - 1}{x} = \frac{6 x + 3}{2 x + 2}$ .

RCTngu8C1onNx

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rozwiązanie

Równanie $\frac{24}{x + 3} = \frac{18}{2 x - 1}$ , przekształcamy do postaci:

$24 \cdot (2 x - 1) = 18 \cdot (x + 3)$ .

Zatem:

$48 x - 24 = 18 x + 54$ ,

$30 x = 78$ .

Zatem $x = 2, 6$ .

Sprawdzenie:
$\frac{24}{2, 6 + 3} = \frac{18}{2 \cdot 2, 6 - 1}$ ,
$\frac{24}{5, 6} = \frac{18}{4, 2}$ ,
$24 \cdot 4, 2 = 18 \cdot 5, 6$ ,
$100, 8 = 100, 8$ .
Równanie $\frac{3 x - 1}{x} = \frac{6 x + 3}{2 x + 2}$ przekształcamy do postaci:

$(3 x - 1) \cdot (2 x + 2) = x \cdot (6 x + 3)$ .

Zatem:

$6 x^{2} + 6 x - 2 x - 2 = 6 x^{2} + 3 x$ ,

$4 x - 2 = 3 x$ .

Wobec tego $x = 2$ .

Sprawdzenie:
$\frac{3 \cdot 2 - 1}{2} = \frac{6 \cdot 2 + 3}{2 \cdot 2 + 2}$ ,
$\frac{5}{2} = \frac{5}{2}$ .

Gra edukacyjna

Zagraj w grę, a następnie wykonaj poniższe polecenia.

RrzHjI7p7v7qW

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zastosowanie wielkości wprost proporcjonalnych - poziom 1.710.580Brawo! Potrafisz wykorzystać wiedzę na temat wielkości wprost proporcjonalnych do rozwiązywania zagadnień z życia codziennego.Niestety! Nie udało CI się zaliczyć testu. Spróbuj jeszcze raz.

Test

Zastosowanie wielkości wprost proporcjonalnych - poziom 1.

Liczba pytań:

Limit czasu:

10.5 min

Pozostało prób:

1/1

Twój ostatni wynik:

Zastosowanie wielkości wprost proporcjonalnych - poziom 2.710.580Brawo! Potrafisz zapisać proporcję, określić czy wielkości są wprost proporcjonalne oraz wykorzystać te wielkości do rozwiązywania zadań tekstowych.Niestety! Nie udało CI się zaliczyć testu. Spróbuj jeszcze raz.

Test

Zastosowanie wielkości wprost proporcjonalnych - poziom 2.

Liczba pytań:

Limit czasu:

10.5 min

Pozostało prób:

1/1

Twój ostatni wynik:

Polecenie 1

R1GOiwTEsJ2FW

Ilustracja przedstawia kilkanaście sztabek złota. — Źródło: Pexels.com, licencja: CC BY 3.0.

R1QNOchKgyKQr

Przeciągnij i upuść lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej, aby uzupełnić zdania. Karat, tak samo jak próba, jest określeniem zawartości czystego złota w danej próbce metalu.

9

- złoto tj. próby

375

. Sztabka złota tej próby o masie

6 g

kosztuje

1440 zł

. Zatem:
a) za sztabkę złota tej próby o masie

25 g

należy zapłacić 1.

5000 zł

, 2.

7500 zł

, 3.

75 g

, 4.

84 g

.
b) za kwotę

20160 zł

można kupić 1.

5000 zł

, 2.

7500 zł

, 3.

75 g

, 4.

84 g

złota tej próby.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 2

Wiadomo, że wielkości $a$ i $b$ zapisane w tabeli są wprost proporcjonalne. Oblicz wartość $x$ .

$a$	$b$
$4 x - 3$	$5$
$- 3 x + 6$	$4$

Do wyznaczenia wartości $x$ rozwiąż równanie $\frac{4 x - 3}{5} = \frac{- 3 x + 6}{4}$ .

Układamy i rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{4 x - 3}{5} = \frac{- 3 x + 6}{4}$

$4 \cdot (4 x - 3) = 5 \cdot (- 3 x + 6)$

$16 x - 12 = - 15 x + 30$

$31 x = 42$

Wobec tego $x = \frac{42}{31} = 1 \frac{11}{31}$ .

Polecenie 3

Odcinek długości $90 cm$ podzielono na dwie części w stosunku $7 : 11$ . Oblicz różnicę długości pomiędzy częściami tego odcinka.

Dany odcinek o długości $90 cm$ możemy podzielić na odcinki o długościach: $x cm$ oraz $(90 - x) cm$ .

Wprowadźmy następujące oznaczenia:

$x -$ długość pierwszej części odcinka wyrażona w $cm$ ,

$90 - x -$ długość drugiej części odcinka wyrażona w $cm$ .

Układamy i rozwiązujemy równanie zapisane w postaci proporcji:

$\frac{x}{90 - x} = \frac{7}{11}$

Zatem:

$11 \cdot x = 7 \cdot (90 - x)$

$11 x = 630 - 7 x$

$18 x = 630$

$x = 35$

$90 - x = 55$

Zatem odcinek o długości $90 c m$ podzielono na odcinki o długościach $35 cm$ i $55 c m$ .

Obliczamy różnicę długości tych odcinków:

$55 c m - 35 c m = 20 c m$

Odpowiedź:
Różnica długości wyznaczonych odcinków wynosi $20 cm$ .

RuIDzckVr1XdK

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RrdXmhfsyNmpZ

Ćwiczenie 2

Wstaw w tekst odpowiednie liczby. Wiadomo, że na przejechanie

100 km

samochód potrzebuje

8 l

benzyny. Wówczas:
- na przejechanie

250 km

potrzeba 1.

125

, 2.

450

, 3.

350

, 4.

6

, 5.

40

, 6.

20

litrów benzyny,
- po wlaniu do pustego baku

30 l

benzyny samochód może przejechać trasę 1.

125

, 2.

450

, 3.

350

, 4.

6

, 5.

40

, 6.

20

,
- na przejechanie

75 km

potrzeba 1.

125

, 2.

450

, 3.

350

, 4.

6

, 5.

40

, 6.

20

litrów benzyny,
- po wlaniu do pustego baku

10 l

benzyny samochód może przejechać trasę 1.

125

, 2.

450

, 3.

350

, 4.

6

, 5.

40

, 6.

20

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1IC7O61LptTN

Ćwiczenie 3

Rozwiąż zadania i uzupełnij odpowiedzi liczbami. Samochód przebył trasę długości

390 km

ze średnią prędkością

65 \frac{km}{h}

. a) Ile czasu zajęło mu pokonanie tej trasy? Odpowiedź: Tu uzupełnij godzin. b) Jaką trasę pokona ten samochód jadąc z tą samą prędkością w ciągu

7

godzin. Odpowiedź: Tu uzupełnij godzin. c) W jakim czasie samochód pokona trasę

195 km

? Odpowiedź: Tu uzupełnij godzin. d) Jaką trasę pokona ten samochód jadąc z tą samą prędkością w ciągu

12

godzin? Odpowiedź: Tu uzupełnij godzin.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1BfOiJQIcfMK

Ćwiczenie 4

Wiadomo, ze wielkości występujące po obu stronach równania są wprost proporcjonalne. Połącz w pary równanie z jego rozwiązaniem.

\frac{x + 2}{x + 1} = \frac{x + 4}{x + 2}

Możliwe odpowiedzi: 1.

x = 0

, 2.

x = \frac{12}{5}

, 3.

x = 3

, 4.

x = 17

\frac{4}{x} = \frac{9}{x + 3}

Możliwe odpowiedzi: 1.

x = 0

, 2.

x = \frac{12}{5}

, 3.

x = 3

, 4.

x = 17

\frac{2}{x + 1} = \frac{3}{x + 3}

Możliwe odpowiedzi: 1.

x = 0

, 2.

x = \frac{12}{5}

, 3.

x = 3

, 4.

x = 17

\frac{x + 5}{2} = \frac{2 x - 1}{3}

Możliwe odpowiedzi: 1.

x = 0

, 2.

x = \frac{12}{5}

, 3.

x = 3

, 4.

x = 17

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1PBD2DPIz39R

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RW8sSe0cIieSi

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

Zaznacz zdania, które są prawdziwe.

Rf4xTQX2R4Ate

Ilustracja przedstawia zegar wskazujący godzinę dziesiątą jedenaście i osiem sekund. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RCbGqjsephl8C

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

R1IES6fZHUzQd

Ilustracja przedstawia koszyk wypełniony świątecznymi piernikami. — Źródło: Pexels.com, licencja: CC BY 3.0.

Do wykonania $60$ sztuk pierniczków potrzeba:

$\frac{1}{4}$ szklanki miodu,

$80 g$ masła,

$\frac{1}{2}$ szklanki brązowego cukru,

$4$ jajka,

$2 \frac{1}{4}$ szklanki mąki pszennej.

Oblicz, ilość poszczególnych składników potrzebnych do wykonania $45$ sztuk pierniczków.

RyKvoN5qZXcfb

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Do wykonania $45$ sztuk pierniczków potrzeba $\frac{45}{60} = \frac{3}{4}$ ilości każdego ze składników.

Niech $x$ oznacza liczbę szklanek miodu.

Zatem:

$\frac{\frac{1}{4}}{60} = \frac{x}{45}$ , czyli $x = \frac{45 \cdot \frac{1}{4}}{60} = \frac{3}{16}$

Niech $y$ oznacza ilość masła w gramach.

Zatem:

$\frac{80}{60} = \frac{y}{45}$ , czyli $y = \frac{80 \cdot 45}{60} = 60$

Niech $z$ oznacza ilość szklanek brązowego cukru.

Zatem:

$\frac{\frac{1}{2}}{60} = \frac{z}{45}$ czyli $z = \frac{\frac{1}{2} \cdot 45}{60} = \frac{3}{8}$

Niech $t$ oznacza ilość jajek.

Zatem:

$\frac{4}{60} = \frac{t}{45}$ , czyli $t = \frac{4 \cdot 45}{60} = 3$

Niech $w$ oznacza ilość szklanek mąki pszennej.

Zatem:

$\frac{2 \frac{1}{4}}{60} = \frac{w}{45}$ , czyli $w = \frac{2 \frac{1}{4} \cdot 45}{60} = \frac{27}{16} = 1 \frac{9}{16}$

Odpowiedź:
Do przygotowania $45$ pierniczków potrzeba $\frac{3}{16}$ szklanki miodu, $60 g$ masła, $\frac{3}{8}$ szklanki brązowego cukru, $3$ jajka i $1 \frac{9}{16}$ szklanki mąki pszennej.

Ćwiczenie 8

Rozwiąż zadania:

$18$ litrów paliwa kosztuje $104, 40 zł$ . Ile trzeba zapłacić za $30$ litrów tego paliwa?
Dźwięk błyskawicy w ciągu pięciu sekund pokonuje drogę około $1655 m$ . W jakiej odległości od domu Pawła uderzył piorun jeśli od błysku do grzmotu minęło $17$ sekund?

R1LRvpLY11a6W

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeżeli przez $x$ oznaczymy kwotę, jaką należy zapłacić za $30$ litrów tego paliwa, to rozwiązujemy równanie, zapisane w postaci proporcji:

$\frac{104, 4}{18} = \frac{x}{30}$ .

Równanie przekształcamy do postaci:

$18 \cdot x = 104, 4 \cdot 30$ .

Zatem $x = 174$ .

Odpowiedź:
Za $30$ litrów paliwa należy zapłacić $174 zł$ .
Jeżeli przez $x$ oznaczymy drogę, jaką po $17$ sekundach pokona dźwięk błyskawicy, to rozwiązujemy równanie, zapisane w postaci proporcji:

$\frac{1655}{5} = \frac{x}{17}$ , zatem $5 x = 17 \cdot 1655$ .

Wobec tego $x = 5627$ .

Odpowiedź:
Piorun uderzył w odległości około $5627 m$ od domu Pawła.

RFJrLSSmSWtP7

Ćwiczenie 9

$\frac{3}{4} = \frac{16}{12}$
$\frac{3}{4} = \frac{12}{16}$
$\frac{4}{16} = \frac{3}{12}$
$\frac{12}{4} = \frac{16}{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1PIDB8z0Qz5x

Ćwiczenie 10

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 11

RQuUgNWNK13r6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1PyR98ySQ2Un

Jaka liczba wstawiona w miejsce

x

pozwoli na otrzymanie proporcji? Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Aby wyrażenie

\frac{3}{4} = \frac{x}{12}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.Aby wyrażenie

\frac{1}{4} = \frac{0, 5}{x}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.Aby wyrażenie

\frac{x}{8} = \frac{2}{1, 6}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.Aby wyrażenie

\frac{5}{x} = \frac{25}{1}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.Aby wyrażenie

\frac{2, 5}{7, 5} = \frac{1}{x}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.Aby wyrażenie

\frac{x}{3} = \frac{2, 6}{3, 9}

stanowiło proporcję, w miejsce

x

należy wstawić liczbę Tu uzupełnij.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R8dJ0PDEOL0Vm

Ćwiczenie 12

Rozwiąż równania. Połącz równanie z poprawnym wynikiem.

\frac{x}{2} = \frac{x - 1}{5}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

\frac{2 x - 1}{3} = \frac{0, 5}{2}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

\frac{3 (x - 1)}{4} = \frac{2 x + 1}{2}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

\frac{3}{2 - 3 x} = \frac{- 2}{4 x}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

\frac{0, 3}{3 x} = \frac{0, 2}{1 - x}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

\frac{- 4 x + 1}{- 2} = \frac{1, 5 x + 1}{3}

Możliwe odpowiedzi: 1.

\frac{1}{3}

, 2.

\frac{5}{9}

, 3.

\frac{7}{8}

, 4.

- \frac{2}{3}

, 5.

- 5

, 6.

\frac{- 2}{3}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R6TsV1ErxlDGx

Ćwiczenie 13

$4 \frac{3}{8}$
$3$
$2$
$4 \frac{2}{7}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R3VyL5FZwbFqr

Ćwiczenie 14

$9$
$27$
$12$
nie da się tego określić

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RDw4tH2btVhCs

Ćwiczenie 15

$13$
$12$
$14$
$15$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1XA6flAYg5mZ

Ćwiczenie 16

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RtUFbf2dCZlHy

Ćwiczenie 17

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R48qfuLPzo1Tv

Ćwiczenie 18

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RyamZq2tNejzL

Ćwiczenie 19

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Słownik

proporcja

równość dwóch ilorazów liczb.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

1. Wielkości wprost proporcjonalne

3. Podział proporcjonalny