Poznajemy bryły
3. Własności graniastosłupów prostych
Graniastosłupy są jednymi z częściej wykorzystywanych brył w życiu codziennym. Ich regularne kształty, w szczególności prostopadłościanu i graniastosłupów prawidłowych, są łatwe do odtworzenia i bardzo funkcjonalne, co stanowi inspirację dla architektów, konstruktorów i wytwórców. Trudno sobie wyobrazić jakiekolwiek miasto lub mieszkanie, w którym nie znajdowałyby się graniastosłupy: ich kształty znajdziemy w bryłach budowli, mebli, pudełek i wielu innych przedmiotach codziennego użytku.

Z własności brył, które poznajecie na lekcjach matematyki korzystamy w życiu codziennym w sposób intuicyjny.
W tym materiale poznasz podstawowe własności graniastosłupów prostych. Nauczysz się je rozpoznawać i nazywać. Swoją wiedzę utrwalisz rozwiązując ćwiczenia.
Zapoznaj się z poniższą animacją, która przedstawia graniastosłupy proste.
Film dostępny pod adresem /preview/resource/Rf8IS7i4yozAE
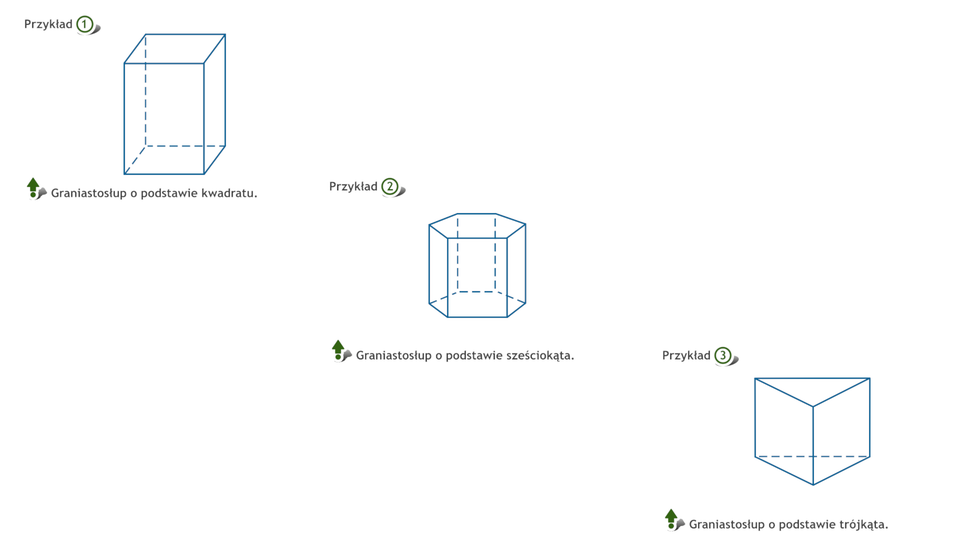
Animacja pokazuje przykłady trzech różnych graniastosłupów.
Graniastosłup prosty to figura przestrzenna, która ma
dwie podstawy będące jednakowymi wielokątami,
ściany boczne będące prostokątami.
Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.

Elementy graniastosłupa prostego.

Możemy spotkać się również z przestrzennymi figurami, które są pochyłe.
Zapoznaj się z poniższą animacją, która pokazuje proste i pochyłe figury przestrzenne.

Film dostępny pod adresem /preview/resource/RAIKhCIixlJ9x
Animacja 3D pokazuje prostopadłościan i ostrosłup trójkątny, które obracają się.
Rodzaje graniastosłupów
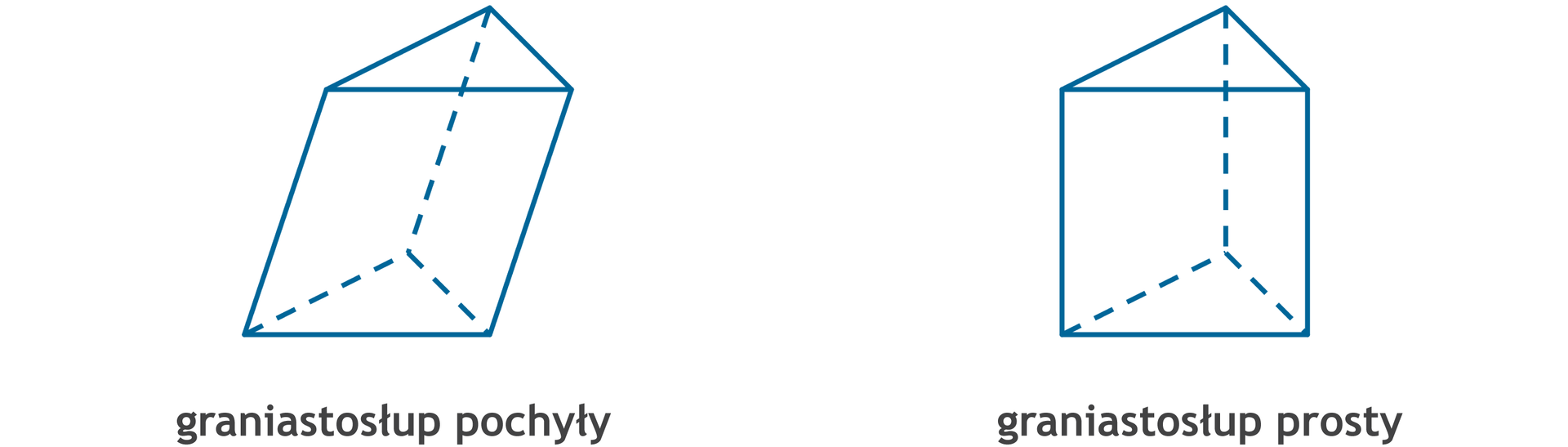
Zapoznaj się z poniższymi rysunkami i wykonaj ćwiczenia do każdego z nich.
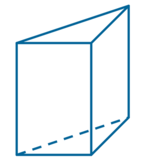
Graniastosłup prosty trójkątny
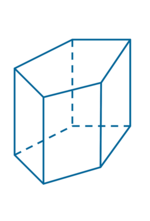
Graniastosłup prosty pięciokątny
Graniastosłup prosty sześciokątny
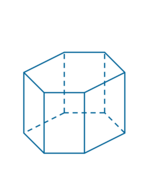
Przeciągnij i upuść.
prostokątami, ścian, trzy, równoległe, podstaw graniastosłupa, prostopadłe, dwie, kwadratami, krawędzi podstawy, równoległobakami, płaska, przestrzenna
Graniastosłup prosty to figura .............................................. , która ma .............................................. jednakowe podstawy będące wielokątami i tyle krawędzi bocznych, ile ...............................................
Ściany boczne graniastosłupa prostego są ...............................................
Podstawy graniastosłupa prostego są do siebie .............................................. , a krawędzie boczne są .............................................. do krawędzi podstawy.
Podobnie, ściany boczne są prostopadłe do ...............................................
Która figura przedstawia graniastosłup prosty?

- Figura
- Figura
- Figura
Graniastosłup pochyły sześciokątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Graniastosłup prosty trójkątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Graniastosłup prosty czworokątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Graniastosłup pochyły trójkątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Graniastosłup prosty sześciokątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Graniastosłup pochyły czworokątny ma w podstawie 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt, a jego ściany to 1. trójkąt, 2. równoległoboki, 3. sześciokąt, 4. równoległoboki, 5. równoległoboki, 6. czworokąt, 7. prostokąty, 8. trójkąt, 9. prostokąty, 10. prostokąty, 11. czworokąt, 12. sześciokąt.
Zapoznaj się z poniższym rysunkiem przedstawiającym pewien graniastosłup prosty sześciokątny.

Zapoznaj się z rysunkiem poniżej.
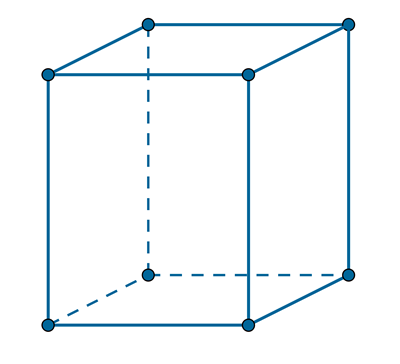
Zapoznaj się z poniższym rysunkiem przedstawiającym pewien graniastosłup prosty trójkątny.

Oblicz sumę długości krawędzi bocznych oraz sumę długości krawędzi obu podstaw graniastosłupa przedstawionego na rysunku.

Odpowiedź: Jest to 1. Tak, 2. sześcian, 3. graniastosłup pięciokątny, 4. równoległościan, 5. Nie.
Czy graniastosłup, którego podstawą jest trójkąt o bokach długości , i , ma ściany boczne o jednakowych wymiarach?
Odpowiedź: 1. Tak, 2. sześcian, 3. graniastosłup pięciokątny, 4. równoległościan, 5. Nie.
Ile graniastosłupów o podstawie czworokątnej widzisz na rysunku?

1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami., ponieważ 1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami.W graniastosłupie prostym wierzchołków jest więcej niż krawędzi.
1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami., ponieważ 1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami.W graniastosłupie prostym podstawy mogą być kwadratami.
1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami., ponieważ 1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami.Istnieje graniastosłup prosty, który ma wierzchołków.
1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami., ponieważ 1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami.Istnieje graniastosłup prosty, który ma krawędzie oraz ścian.
1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami., ponieważ 1. Tak, 2. graniastosłup dwudziestokątny ma krawędzi., 3. Nie, 4. kwadrat jest prostokątem., 5. Tak, 6. Nie, 7. Tak, 8. graniastosłup osiemnastokątny ma krawędzie., 9. Nie, 10. podstawy mogą być dowolnymi wielokątami., 11. kwadrat nie jest prostokątem., 12. wierzchołków jest tyle samo co krawędzi., 13. Nie, 14. liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od ., 15. krawędzi jest raza więcej niż wierzchołków., 16. liczba wierzchołków graniastosłupa jest zawsze parzysta., 17. wszystkie ściany graniastosłupa są prostokątami.
Wybierz z listy poprawne odpowiedzi oraz ich uzasadnienia.
liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od 3., Tak, Nie, liczba wierzchołków graniastołupa jest zawsze parzysta., kwadrat jest prostokątem., Nie, Tak, Nie, kwadrat nie jest prostokątem, podstawy mogą być dowolnymi wielokątami., Nie, krawędzi jest 1,5 raza wicej niż wierzchołków., Tak, wszystkie ściany graniastosłupa są prostokątami., wierzchołków jest tyle samo co krawędzi., graniastosłup osiemnastokątny ma 54 krawędzie., graniastosłup dwudziestokątny ma 60 krawędzi.
a) W graniastosłupie prostym podstawy zawsze są prostokątami.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
b) W graniastosłupie prostym wierzchołków jest więcej niż krawędzi.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
c) W graniastosłupie prostym podstawy mogą być kwadratami.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
d) Istnieje graniastosłup prosty, który ma wierzchołków.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
e) Istnieje graniastosłup prosty, który ma krawędzie oraz ścian.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.