Stosowanie wyrażeń algebraicznych
8. Powtórzenie wiadomości - wyrażenia algebraiczne
Wyrażenia algebraiczne przydają się, gdy chcemy zapisać algorytm rozwiązania problemu, który powtarza się cyklicznie.
Na przykład musimy obliczyć, ile rolek tapety trzeba kupić, aby wystarczyło ich na oklejenie prostokątnej ściany o wymiarach na .

Najpierw oczywiście obliczamy pole powierzchni ściany.
Jedna rolka tapety wystarczy na oklejenie ściany. Ponieważ:
zatem trzeba kupić trzy rolki tapety.
Jeśli chcielibyśmy wytapetować jeszcze inne prostokątne ściany, można powyższe obliczenia zapisać w postaci wzoru:
gdzie:
, – wymiary ściany w metrach.
Musimy jeszcze określić przybliżenie z góry otrzymanej liczby (chyba, że jest to liczba całkowita). Korzystając z tego wzoru, ustalimy szybciej liczbę potrzebnych rolek tapety.
Wyrażenie to wyrażenie algebraiczne.
Wyrażenie algebraiczne to wyrażenie zbudowane z liczb, liter, znaków działań, nawiasów.
Analizując przykłady zawarte w tym materiale, utrwalisz poznasz sposoby zapisywania zależności przedstawionych w zadaniach w postaci wyrażeń algebraicznych. Sprawdzisz ukształtowane umiejętności wykonując ćwiczenia.
Gra edukacyjna
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D106UdUdw
POZIOM ŁATWY. Test z jednomianów i wielomianów.
POZIOM TRUDNY. Test z wielomianów.
Odkryj tę regułę. Z ilu kwadratów składa się dwudziesta z takich figur? Zaznacz prawidłową odpowiedź.
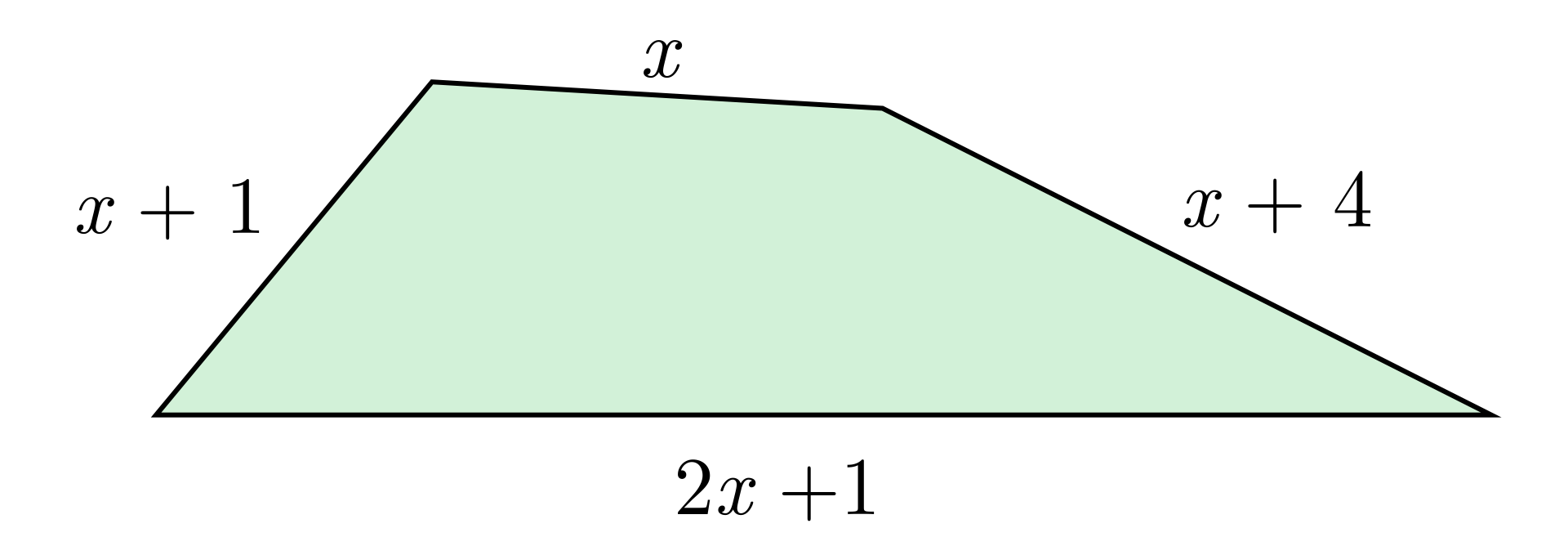
Które z podanych wyrażeń nie opisuje obwodu narysowanego czworokąta? Zaznacz prawidłową odpowiedź.
Zaznacz, które zdanie jest prawdziwe, a które fałszywe.. Najniższa z dziewcząt to Helena.. Możliwe odpowiedzi: Prawda, Fałsz. Najwyższa z dziewcząt to Hanna.. Możliwe odpowiedzi: Prawda, Fałsz. Średnia arytmetyczna wzrostu dziewcząt to .. Możliwe odpowiedzi: Prawda, Fałsz. Helena jest niższa od Hanny o .. Możliwe odpowiedzi: Prawda, Fałsz. Halina jest wyższa od Heleny o .. Możliwe odpowiedzi: Prawda, Fałsz
Sumę dwóch dowolnych liczb różnych od zera pomnożono przez ich różnicę. Do wyniku dodano sumę ich kwadratów. Wykaż, że otrzymana liczba jest dodatnia.
Kolejne figury na rysunku tworzone są z jednakowych kwadratów i sześciokątów takich, jak na rysunku. Pole takiego kwadratu jest równe , a pole sześciokąta .
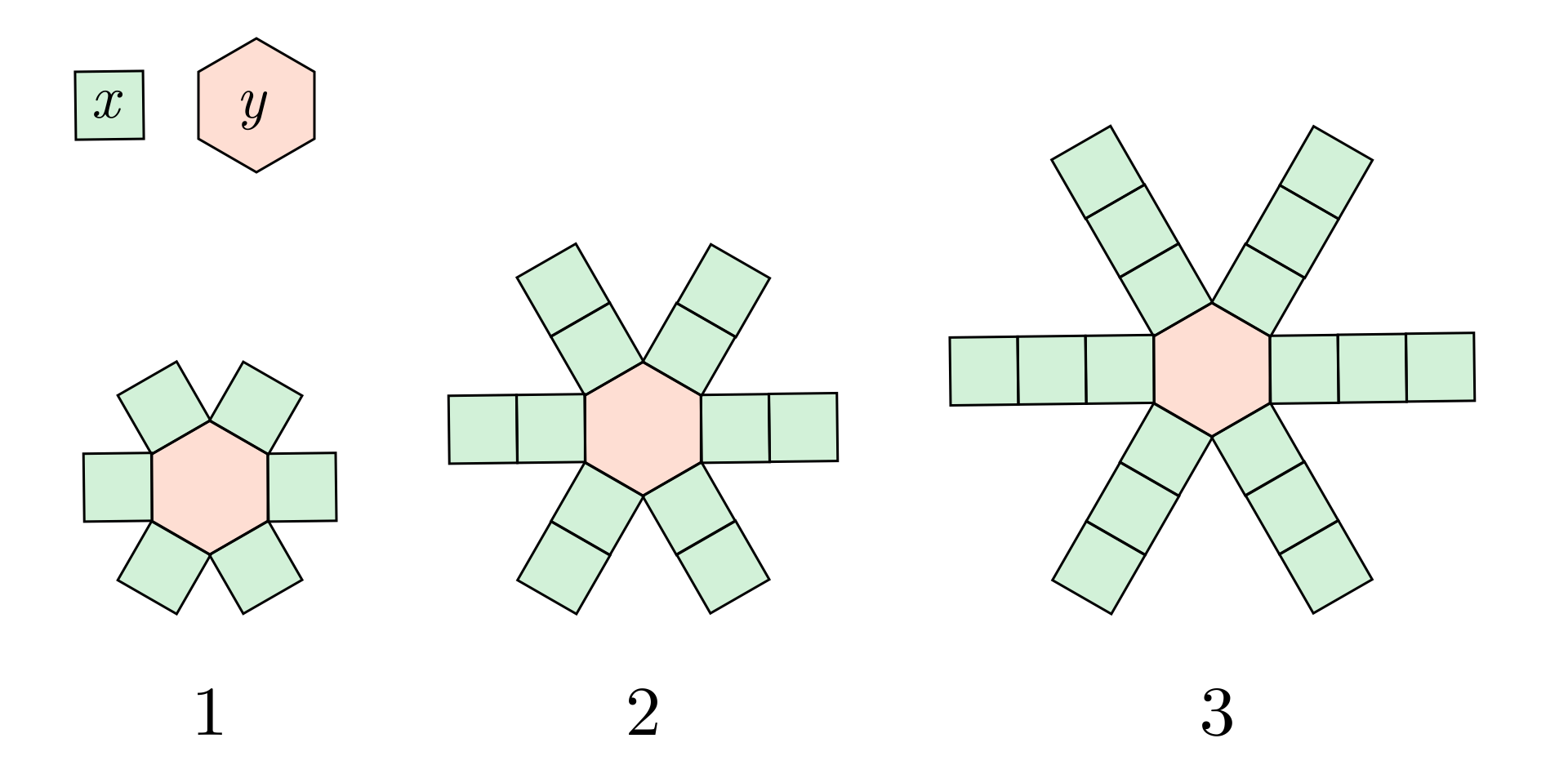
Odkryj regułę, według której tworzone są kolejne figury. Zapisz za pomocą wyrażenia algebraicznego pole –tej takiej figury, gdzie jest liczbą naturalną dodatnią.
Kolejne figury na rysunku tworzone są z jednakowych zapałek według pewnej reguły tak, jak na rysunku.
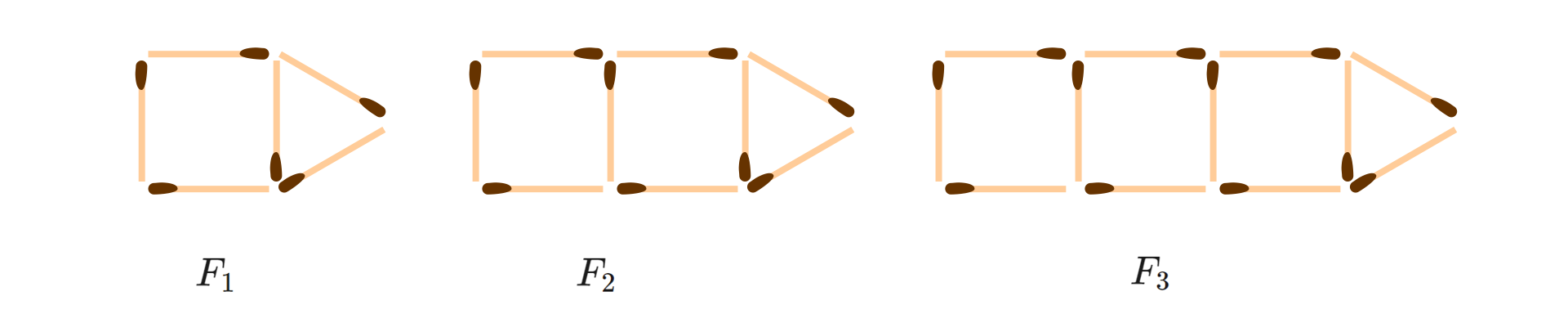
Odkryj tę regułę i zapisz wzór, według którego można obliczyć liczbę zapałek figury o dowolnym numerze. Oblicz, z ilu zapałek zbudowana jest setna taka figura.
Połącz w pary jednomiany przed uporządkowaniem z odpowiadającymi im jednomianami po uporządkowaniu.
<span aria-label="dwa początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, dwa, y indeks górny, dwa, z indeks górny, trzy" role="math"><math><mn>2</mn><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>3</mn></msup></math></span>, <span aria-label="trzy x indeks górny, trzy, y indeks górny, dwa, z indeks górny, dwa" role="math"><math><mn>3</mn><msup><mi>x</mi><mn>3</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>2</mn></msup></math></span>, <span aria-label="początek ułamka, jeden, mianownik, dwa, koniec ułamka, a indeks górny, trzy, b indeks górny, cztery" role="math"><math><mfrac><mn>1</mn><mn>2</mn></mfrac><msup><mi>a</mi><mn>3</mn></msup><msup><mi>b</mi><mn>4</mn></msup></math></span>, <span aria-label=" minus, cztery a b indeks górny, trzy" role="math"><math><mo>-</mo><mn>4</mn><mi>a</mi><msup><mi>b</mi><mn>3</mn></msup></math></span>, <span aria-label="początek ułamka, dwanaście, mianownik, dwadzieścia pięć, koniec ułamka, a indeks górny, trzy, b indeks górny, cztery" role="math"><math><mfrac><mn>12</mn><mn>25</mn></mfrac><msup><mi>a</mi><mn>3</mn></msup><msup><mi>b</mi><mn>4</mn></msup></math></span>, <span aria-label="trzy początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, trzy, y indeks górny, dwa, z indeks górny, trzy" role="math"><math><mn>3</mn><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>3</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>3</mn></msup></math></span>, <span aria-label=" minus, osiem a b indeks górny, trzy" role="math"><math><mo>-</mo><mn>8</mn><mi>a</mi><msup><mi>b</mi><mn>3</mn></msup></math></span>
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Przeciągnij i upuść odpowiednie jednomiany tak, aby prawdziwe były podane równości.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
Od tej liczby odjęto liczbę trzycyfrową o cyfrze setek cyfrze dziesiątek i cyfrze jedności . Zapisz za pomocą wyrażenia algebraicznego liczbę będącą wynikiem tego odejmowania. Uzupełnij poniższą odpowiedź, przeciągając w lukę odpowiedni jednomian. Odpowiedź: Wynik odejmowania wynosi 1. , 2. , 3. , 4. .
Wykonaj działania.
Przeciągnij i upuść jednomiany tak, aby podane równości były prawdziwe.
, , , , ,
a) ............
b) ............
c) ............
d) ............
- Pole prostokąta o bokach i wynosi .
- Wynikiem działania jest .
- Objętość sześcianu o krawędzi wynosi .
- Kwadrat liczby jest o większy od kwadratu liczby .
- Wyrażenia i są równe.
Połącz w pary.
<math><mn>4</mn><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><mn>9</mn><msqrt><mn>6</mn></msqrt><mi>x</mi></math>, <math><mn>3</mn><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><mn>2</mn><msqrt><mn>6</mn></msqrt><mi>x</mi><mo>+</mo><mn>2</mn></math>, <math><mn>3</mn><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><msqrt><mn>6</mn></msqrt><mi>x</mi><mo>-</mo><mn>4</mn></math>, <math><mo>-</mo><mn>12</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>2</mn><msqrt><mn>6</mn></msqrt><mi>x</mi><mo>-</mo><mn>6</mn></math>, <math><msqrt><mn>6</mn></msqrt><mi>x</mi><mo>-</mo><mn>7</mn><msup><mi>x</mi><mn>2</mn></msup></math>
Odpowiedź: Wynik to 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Odpowiedź: Wynik to 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Odpowiedź: Wynik to 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Dane są dwa wielokąty i . O ile pole wielokąta jest większe od pola wielokąta ?

Odpowiedź: Pole 1. trójkąta prostokątnego, 2. , 3. , 4. , 5. , 6. prostokąta jest większe o 1. trójkąta prostokątnego, 2. , 3. , 4. , 5. , 6. prostokąta.
Odpowiedź: Tą liczbą jest 1. , 2. , 3. , 4. , 5. , 6. .
Odpowiedź: Różnica wydatków jest ukazana równaniem1. , 2. , 3. , 4. .
Jaka jest wysokość trapezu przedstawionego na rysunku, jeżeli wiadomo, że jego pole jest równe ?
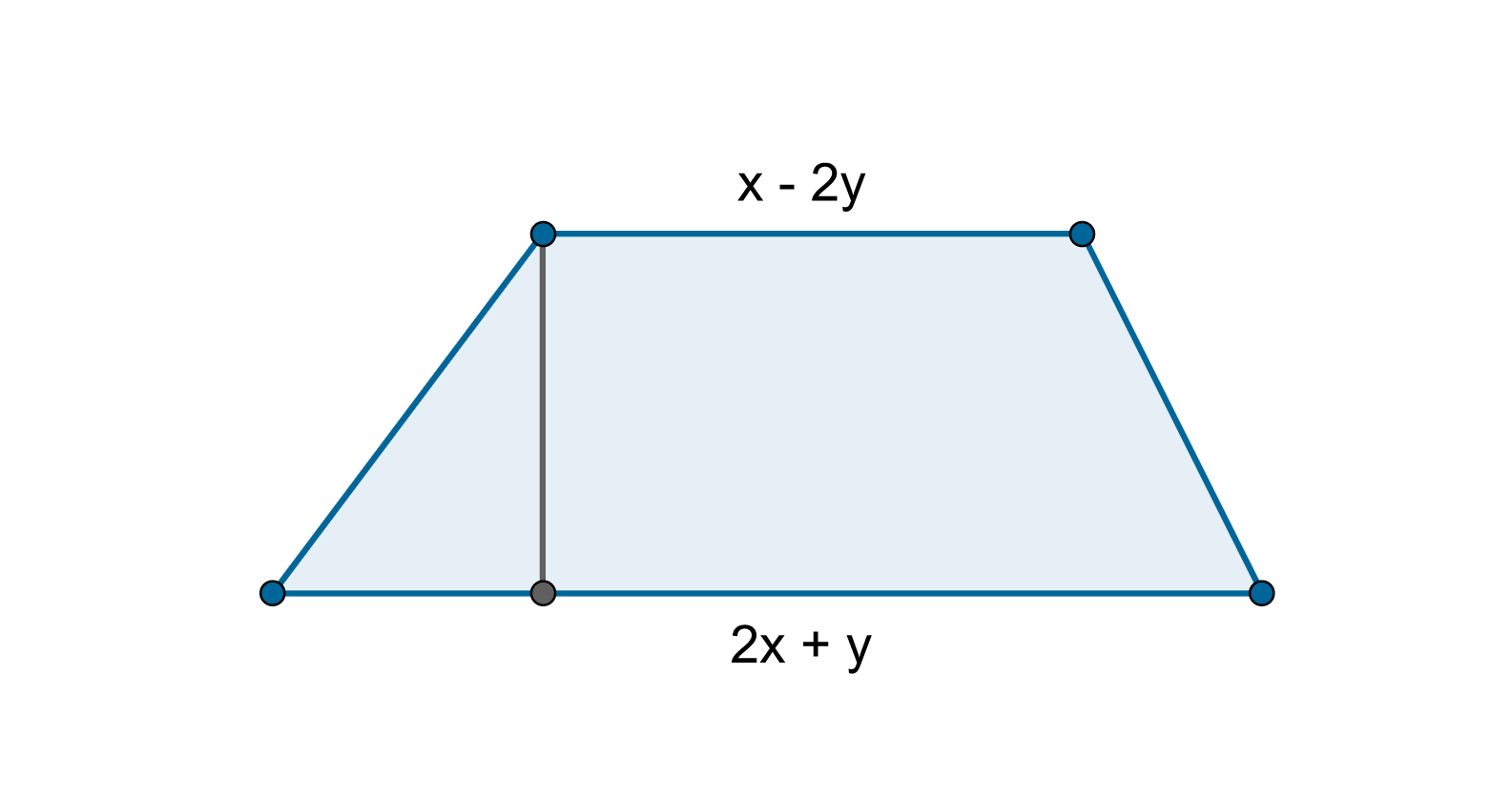
Zapisz w najprostszej postaci wyrażenie, opisujące pole pięciokąta .

Rysunek przedstawia trapez.

Test samosprawdzający
Rozwiąż test, którego celem jest usystematyzowanie wiadomości i umiejętności na temat wyrażeń algebraicznych.
Test jest dwustopniowy. Drugą, trudniejszą część testu, możesz rozwiązać dopiero, gdy zaliczysz
część łatwiejszą.
Wyrażenia algebraiczne cz.2
Wyrażenia algebraiczne cz.2