Wyodrębnianie cyfr z danej liczby
W pozycyjnym systemiepozycyjnym systemie liczbowym ta sama cyfra może odpowiadać za różne wartości. Zależy to od pozycji, na której się znajduje.
W systemie dziesiętnym do zapisu dowolnej liczby wykorzystujemy 10 cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Umiejętność wyodrębniania kolejnych cyfr liczby może być przydatna podczas rozwiązywania problemów algorytmicznych badających własności liczb.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
MultimediumMultimedium
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
BibliografiaBibliografia
ogólne zasady tworzenia programów w języku ScratchScratch;
zasady dzielenia całkowitegodzielenia całkowitego;
zasady obliczania reszty z dzielenia (znajdziesz je w e‑materiale dotyczącym dzielenia z resztądzielenia z resztą),
algorytm wyodrębniania cyfr z danej liczby zapisany w językach Python oraz Blockly; zaprezentowany zostałe w e‑materiale Scratch (Blockly)Scratch (Blockly).
Zapoznasz się z algorytmem wyodrębniania cyfr liczby.
Korzystając z języka ScratchScratch, zapiszesz program, w którym wykorzystasz algorytm wyodrębniania cyfr liczby.
Wymienisz różnice między cyfrą najmniej i najbardziej znaczącą.
Problem
Dana jest liczba naturalna. Wyodrębnij jej cyfry i wypisz je na ekranie, zaczynając od cyfry jedności (tzw. najmniej znaczącej cyfry).
Specyfikacja problemu:
Dane:
a– liczba naturalna
Wynik:
kolejne cyfry liczby; na początku powinna znajdować się najmniej znacząca cyfra
Analiza problemu
Najmniej znaczącą cyfrę danej liczby naturalnej otrzymamy, obliczając resztę z dzielenia tej liczby przez liczbę 10. Jeżeli w kolejnym kroku podzielimy tę liczbę całkowicie przez 10, to otrzymamy liczbę 10 razy mniejszą (usuniemy cyfrę jedności, a cyfra dziesiątek pierwotnej liczby stanie się cyfrą jedności). Obliczając resztę z dzielenia przez 10 tak powstałej liczby otrzymamy kolejną najmniej znaczącą cyfrę. W ten sposób możemy wyodrębnić wszystkie cyfry.
Schemat blokowy algorytmualgorytmu wyodrębniania cyfr liczby naturalnej.
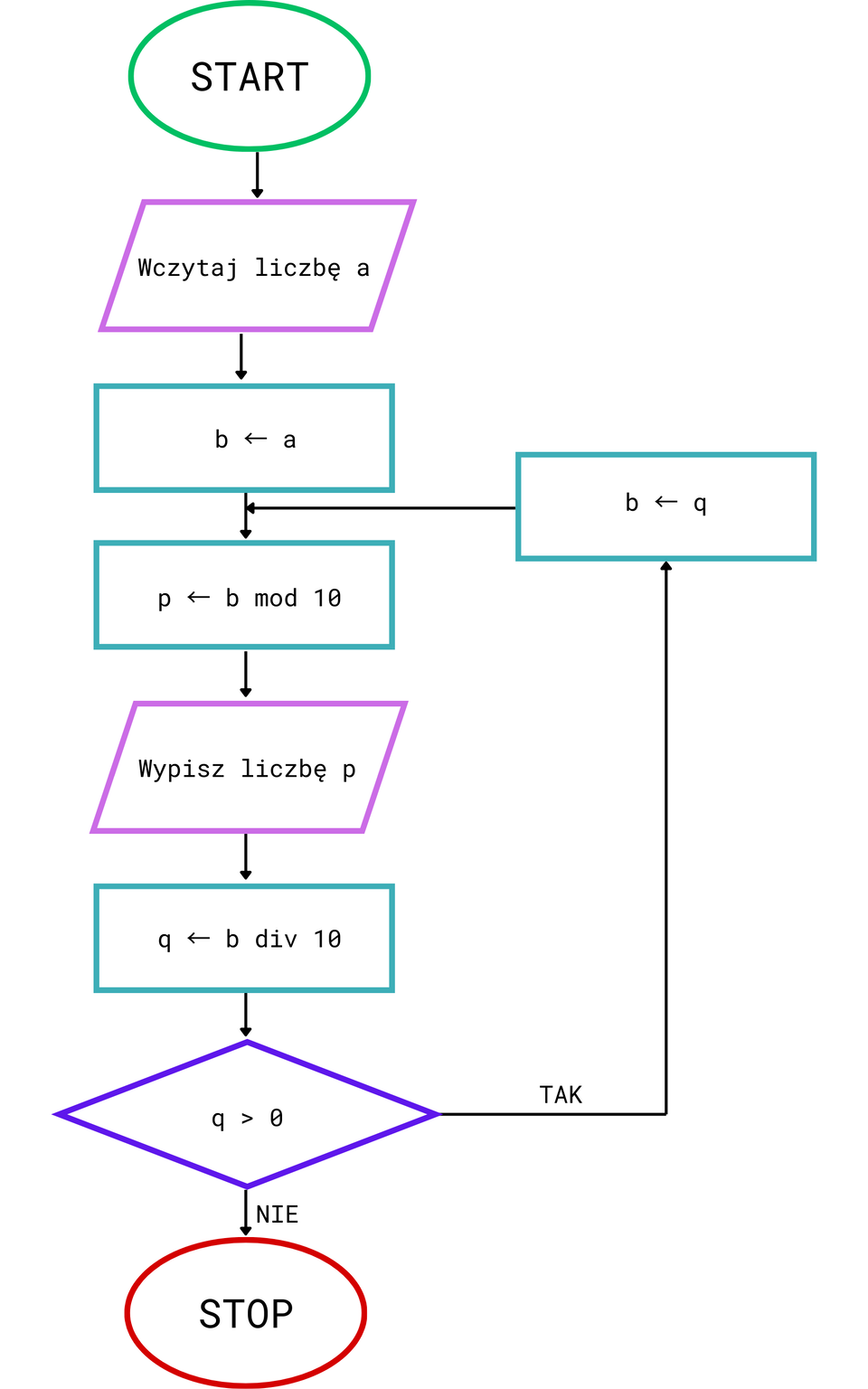
W schemacie wykorzystaliśmy operatory div oraz mod.
Operator div to operator dzielenia całkowitego.
Operator mod to operatora obliczania reszty z dzielenia (modulo).
Przeanalizujmy algorytmalgorytm zapisany za pomocą schematu blokowego i wykonajmy przykładowe obliczenia dla liczby 8394:
Wczytujemy liczbę naturalną
a.Przypisujemy do liczby
bwartość liczbya.Obliczamy wartość reszty z dzielenia liczby
bprzez 10. Obliczoną wartość przypisujemy dop.Wypisujemy wartość
p.Dzielimy bez reszty
bprzez 10. Wynik przypisujemy do zmiennejq.Sprawdzamy, czy
qjest większe niż 0.Jeśli tak, przypisujemy
bwartośćqi wracamy do kroku 3. Jeśli nie, przechodzimy do kroku 8.Kończymy działanie algorymtu.
Prześledźmy działanie algorytmu dla a = 8394.
Krok |
|
|
|
|
|---|---|---|---|---|
0 | 8394 |
| 8394 mod 10 = 4 | 8394 div 10 = 839 |
1 | 8394 |
| 839 mod 10 = 9 | 839 div 10 = 83 |
2 | 8394 |
| 83 mod 10 = 3 | 83 div 10 = 8 |
3 | 8394 |
| 8 mod 10 = 8 | 8 div 10 = 0 |
4 | 8394 |
|
Wypisane cyfry to: 4 9 3 8.
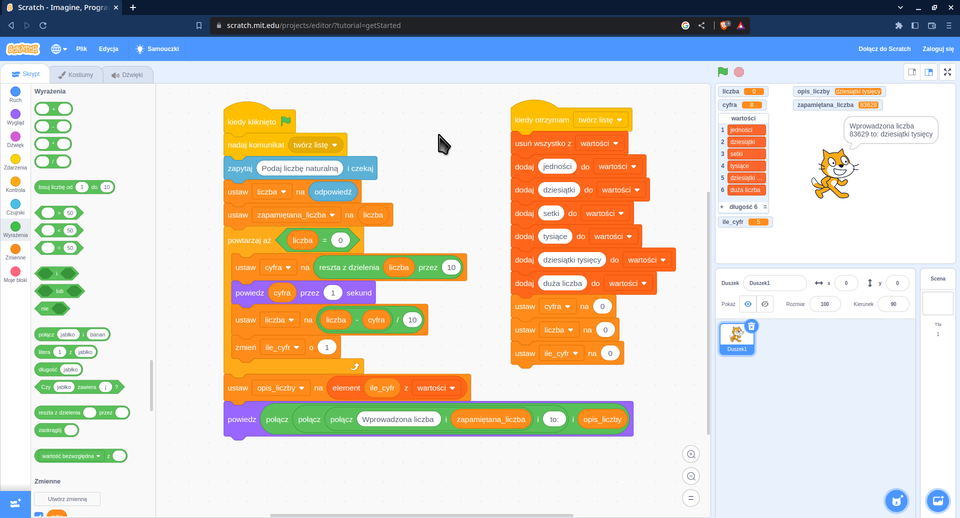
Przykładowy program w języku ScratchScratch, który rozwiązuje problem wyodrębniania cyfr liczby podanej przez użytkownika
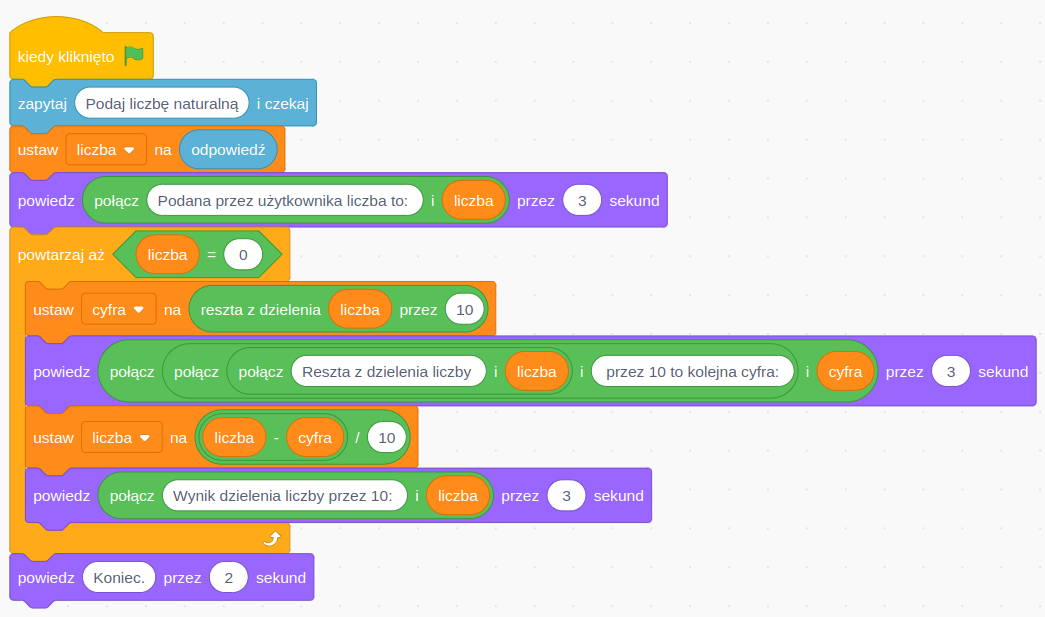
Opis schematu blokowego programu:
Program rozpoczyna się od bloku 'kiedy kliknięto zieloną flagę' na pomarańczowym tle. Kolejne bloki tworzą program, który prosi użytkownika o podanie liczby naturalnej, a następnie wykonuje na niej operacje matematyczne. Program wyświetla wprowadzoną liczbę, po czym w pętli (działającej dopóki liczba nie osiągnie zera) wyznacza cyfrę jedności jako resztę z dzielenia przez 10, wyświetla tę cyfrę, a następnie dzieli liczbę przez 10. Widoczne są kolorowe bloki funkcyjne: pomarańczowe (sterujące), zielone (operacyjne) i fioletowe (wyjściowe). Kod demonstruje algorytm wyodrębniania kolejnych cyfr z liczby naturalnej za pomocą operacji dzielenia i reszty z dzielenia. Program kończy się wyświetleniem napisu 'Koniec'
W języku Scratch nie ma bloku dopóki. W przypadku zaprezentowanego algorytmu zastosujemy konstrukcję powtarzaj aż z warunkiem liczba równe 0. Da to taki sam efekt.
W języku Scratch dzielenie całkowite realizujemy za pomocą następującej konstrukcji:

Inna możliwość to zastosowanie konkretnego bloku odpowiedzialnego za obliczenie podłogi (blok odpowiada operacji liczba div 10):

W języku Python pętlę dopóki realizujemy za pomocą następującej konstrukcji:
Zapoznaj się z filmem, który demonstruje działanie programu dla liczby podanej przez użytkownika:
Film dostępny pod adresem /preview/resource/R14O0qQYxFrHn
Animacja prezentuje działanie programu z zastosowaniem algorytmu wyodrębniania
Program zapisany w języku Scratch 3:
Kod w języku Python:
W e‑materiale Scratch (Blockly)Scratch (Blockly) prezentujemy zapis tego programu w języku Python oraz z wykorzystaniem Blockly.
Pozycyjny system liczbowy
W pozycyjnym systemie liczbowympozycyjnym systemie liczbowym ta sama cyfra może mieć różne znaczenie, w zależności od pozycji, na której ona stoi.
W codziennym życiu używamy systemu dziesiętnego, który do zapisu dowolnej liczby używa cyfr od 0 do 9. Każda cyfra zajmuje określoną pozycję w liczbie, a jej wartość jest mnożona przez odpowiednią potęgę liczby 10 zależną od jej pozycji. Pozycje są wyznaczane od prawej strony (najmniej znaczącej cyfry liczby) – zaczynamy od potęgi zerowej.
W przypadku liczby 532 zapisanej w sytemie dziesiętnym:
cyfra
2znajduje się na miejscu jedności;cyfra
3znajduje się na miejscu dziesiątek;cyfra
5znajduje się na miejscu setek.
Aby obliczyć wartość liczby, sumujemy iloczyny cyfr i odpowiednich potęg liczby 10. W przypadku liczby 532:
Wyobraźmy sobie, że zamiast cyfr stosujemy różne symbole, np.:
Cyfra | Oznaczenie |
|---|---|
| czerwone koło |
| zielony kwadrat |
| pomarańczowa gwiazda |
| żołty trójkąt |
| niebieska gwiazdka |
| różowy sześciokąt |
| zielone słoneczko |
| błękitne serce |
| fioletowa chmura |
| fioletowy krzyżyk |
Oto przykładowe znaki od 0 do 9.

Liczba 854 zapisana zgodnie z przyjętą konwencją:

Liczby 34, 80 oraz 114 zapisane zgodnie z przyjętą konwencją:

Notatnik
Prezentacja multimedialna
Indeks górny Źródło: Adam Jurkiewicz, licencja: CC BY 3.0. Indeks górny koniecŹródło: Adam Jurkiewicz, licencja: CC BY 3.0.
Pobierz program:
Program wyodrębnia kolejne cyfry liczby, zaczynając od cyfry jedności.
Zestaw ćwiczeń interaktywnych
Zapoznaj się z ilustracjami, które przedstawiają dodawanie i odejmowanie pisemne liczb reprezentowanych przez symbole.
Operacja dodawania

Operacja odejmowania

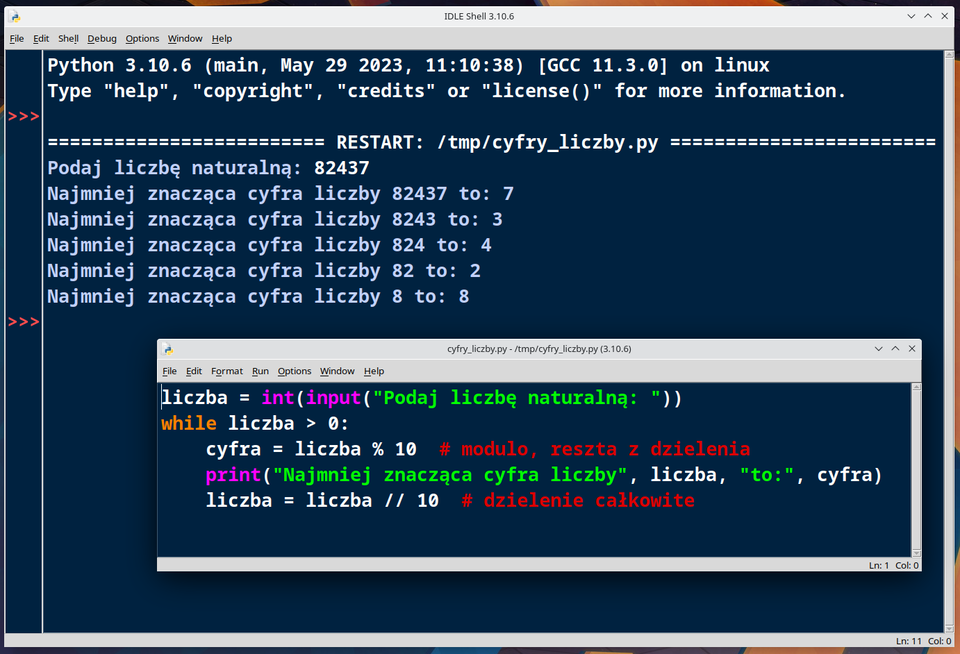
Poniżej przedstawiono kod źródłowy programu wraz z komentarzem. Zadaniem programu jest rozkładanie liczby na cyfry.
liczba = int(input(„Podaj liczbę naturalną: „))
while liczba > 0:
cyfra = liczba % 10 # modulo, reszta z dzielenia
print(„Najmniej znacząca cyfra liczby”, liczba, „to:”, cyfra)
liczba = liczba // 10 # dzielenie całkowite
liczba = int(input(„Podaj liczbę naturalną: „))
Program prosi użytkownika o podanie liczby naturalnej i zapisuje ją jako liczbę całkowitą do zmiennej liczba.
while liczba > 0:
Rozpoczyna się pętla, która działa tak długo, jak długo liczba jest większa od zera.
cyfra = liczba % 10
Zmienna cyfra otrzymuje wartość ostatniej (najmniej znaczącej) cyfry liczby. Obliczane jest to jako reszta z dzielenia liczby przez 10.
Komentarz po prawej stronie: # modulo, reszta z dzielenia.
print(„Najmniej znacząca cyfra liczby”, liczba, „to:”, cyfra)
Program wyświetla informację o aktualnej wartości liczby i jej najmniej znaczącej cyfrze.
liczba = liczba // 10
Liczba jest dzielona całkowicie przez 10 (usuwanie ostatniej cyfry z prawej strony) i przypisywana z powrotem do zmiennej liczba.
Komentarz: # dzielenie całkowite.
Pobierz program:
Pobierz program:
Słownik
ściśle określony, skończony zestaw instrukcji, który służy do rozwiązania problemu lub wykonania zadania
system liczbowy, w którym wartość cyfry zależy od pozycji, na której jest zapisana
wizualny język programowania stworzony przez Mitchela Resnicka, profesora MIT; pierwsza publiczna wersja została wydana w 2007 roku
operacja dzielenia liczb całkowitych polegająca na odrzuceniu części ułamkowej wyniku
Bibliografia
Sysło M.M., Algorytmy, Helion, Gliwice 2016.
Tkaczyk M., Cyfry i liczby, MEiN materiały edukacyjne, Warszawa 2021.




![Grafika przedstawia pionowo ułożone bloki programu w Scratchu, których celem jest sprawdzenie liczby cyfr w podanej przez użytkownika liczbie naturalnej i wyświetlenie odpowiedniego komunikatu.
Szczegółowy opis kodu programu
Start programu
Żółty blok „kiedy kliknięto [zieloną flagę]” uruchamia cały skrypt po naciśnięciu zielonej flagi.
Inicjalizacja zmiennych
Trzy kolejne pomarańczowe bloki ustawiają zmienne na wartość 0:
liczba na 0,
cyfra na 0,
ile_cyfr na 0.
Pobranie danych od użytkownika
Niebieski blok „zapytaj [Podaj liczbę naturalną] i czekaj” – wyświetla pytanie i czeka na odpowiedź użytkownika.
Pomarańczowy blok „ustaw [liczba] na [odpowiedź]” – zapisuje odpowiedź do zmiennej liczba.
Liczenie cyfr w liczbie
Pomarańczowa pętla „powtarzaj aż [liczba = 0]”:
Wewnątrz pętli są trzy bloki:
„ustaw [cyfra] na [reszta z dzielenia (liczba) przez 10]” – oblicza ostatnią cyfrę liczby.
„zmień [ile_cyfr] o 1” – zwiększa licznik cyfr o 1.
„ustaw [liczba] na [(liczba) - (cyfra)] / 10” – usuwa ostatnią cyfrę liczby (dzieli bez reszty).
Sprawdzenie liczby cyfr
Pomarańczowy blok warunkowy „jeżeli [ile_cyfr > 4] to”:
Jeśli liczba cyfr jest większa niż 4:
Fioletowy blok „powiedz [Duża liczba] przez 3 sekundy”.
W przeciwnym razie:
Fioletowy blok „powiedz [Mała liczba] przez 3 sekundy”.
Zakończenie programu
Fioletowy blok „powiedz [Koniec – wartość liczby to 0.] przez 2 sekundy”.](https://static.zpe.gov.pl/portal/f/res-minimized/RRaA71rN0vszE/1751354256/Npi5CLWXjsYqXNPrTlZXJqJqRaT9Yzgc.png)
![Grafika prezentuje zrzut ekranu z edytora Scratch, na którym widoczny jest blokowy kod programu służącego do obliczania sumy cyfr podanej przez użytkownika liczby naturalnej.
Szczegółowy opis kodu programu
Początek programu
Blok żółty „kiedy kliknięto [zieloną flagę]” – uruchamia całość po kliknięciu zielonej flagi.
Inicjalizacja zmiennych
„ustaw [liczba] na 0”
„ustaw [cyfra] na 0”
„ustaw [suma_cyfr] na 0”
Te trzy pomarańczowe bloki ustawiają startowe wartości zmiennych, które będą wykorzystywane w dalszej części programu.
Pobranie danych od użytkownika
Niebieski blok „zapytaj [Podaj liczbę naturalną] i czekaj” – program pyta użytkownika o liczbę.
Pomarańczowy blok „ustaw [liczba] na [odpowiedź]” – ustawia zmienną liczba na wartość podaną przez użytkownika.
Prezentacja liczby
Fioletowy blok „powiedz [Połącz: Podana przez użytkownika liczba to: (liczba)] przez 3 sekundy” – program wyświetla komunikat z podaną liczbą.
Wyznaczanie sumy cyfr
Pomarańczowy blok „powtarzaj aż [liczba = 0]”
„ustaw [cyfra] na [reszta z dzielenia (liczba) przez 10]” – wyodrębnia ostatnią cyfrę liczby.
„zmień [suma_cyfr] o (cyfra)” – dodaje tę cyfrę do zmiennej suma_cyfr.
„ustaw [liczba] na [(liczba) - (cyfra)] / 10” – usuwa ostatnią cyfrę z liczby.
Wyświetlenie wyniku
Fioletowy blok „powiedz [Połącz: Suma wartości cyfr wynosi: (suma_cyfr)] przez 3 sekundy” – program pokazuje użytkownikowi sumę cyfr wpisanej liczby.](https://static.zpe.gov.pl/portal/f/res-minimized/R1ZFmjXE73otk/1751354256/efzv5HQFewmIWvzr9g9Oak6OCKWf5Dx6.png)
![Grafika przedstawia zrzut ekranu z edytora Scratch z widocznym scenariuszem programu służącego do analizy cyfry dziesiątek w podanej przez użytkownika liczbie.
Szczegółowy opis kodu programu
Początek programu
Blok żółty „kiedy kliknięto [zieloną flagę]”, inicjujący działanie skryptu po kliknięciu zielonej flagi.
Pobranie liczby od użytkownika
Blok niebieski „zapytaj [Podaj liczbę naturalną] i czekaj” wyświetla pytanie i oczekuje na wpisanie liczby.
Blok pomarańczowy „ustaw [liczba] na [odpowiedź]” zapisuje wprowadzoną liczbę w zmiennej liczba.
Sprawdzenie, czy liczba ma cyfrę dziesiątek
Blok zielony „jeżeli [liczba < 10] to” sprawdza, czy wpisana liczba jest jednocyfrowa.
Jeśli tak:
Blok fioletowy „powiedz [Brak cyfry dziesiątek] przez 2 sekundy” – program informuje, że nie ma cyfry dziesiątek.
Blok pomarańczowy „zatrzymaj wszystko” kończy dalsze działanie programu.
W przeciwnym razie (jeżeli liczba ma co najmniej dwie cyfry)
Blok pomarańczowy „ustaw [cyfra] na [podłoga z (reszta z dzielenia [liczba] przez 100) / 10]” oblicza cyfrę dziesiątek:
Najpierw obliczana jest reszta z dzielenia liczba przez 100 (czyli dwie ostatnie cyfry liczby),
Następnie dzielona przez 10 i zaokrąglana w dół, aby uzyskać cyfrę dziesiątek.
Blok zielony „jeżeli [reszta z dzielenia [cyfra] przez 2 = 0] to” sprawdza, czy cyfra dziesiątek jest parzysta.
Jeśli tak:
Blok fioletowy „powiedz [Cyfra dziesiątek jest parzysta] przez 2 sekundy” – pojawia się komunikat o parzystości cyfry.
W przeciwnym razie:
Blok fioletowy „powiedz [Cyfra dziesiątek jest nieparzysta] przez 2 sekundy” – pojawia się komunikat o nieparzystości cyfry.](https://static.zpe.gov.pl/portal/f/res-minimized/Ru69ZxqUHAlXx/1751354257/7DUOlYlrApdpIRD1XGzeJVPX2rL8eLYh.png)