Bryły obrotowe
W tym materiale zawarte są informacje na temat brył obrotowych. Poznasz podstawowe definicje i przykłady brył obrotowych. Dowiesz się jak wyznaczyć przekrój osiowy i przekrój poprzeczny w tego typu bryłach.
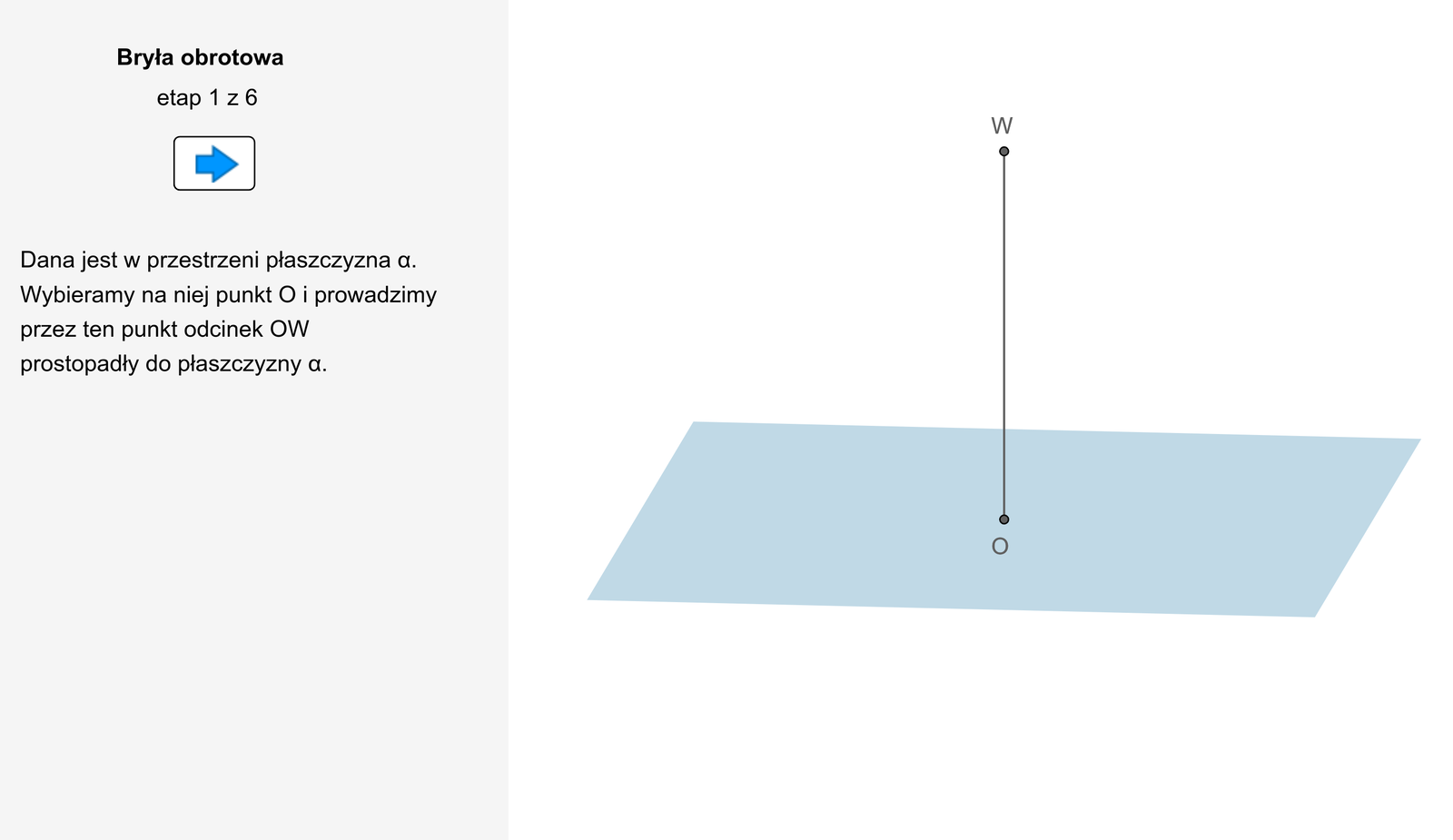
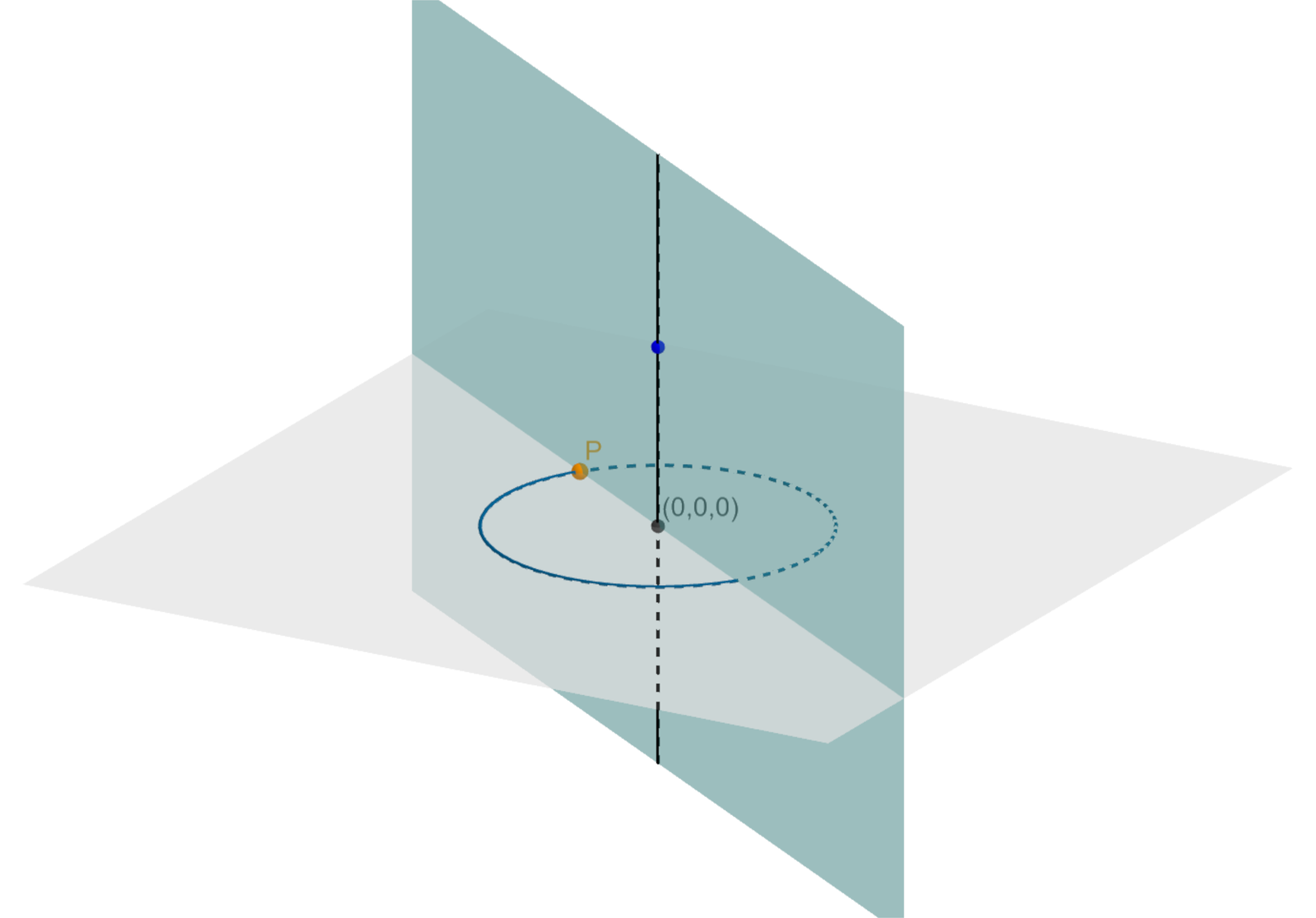
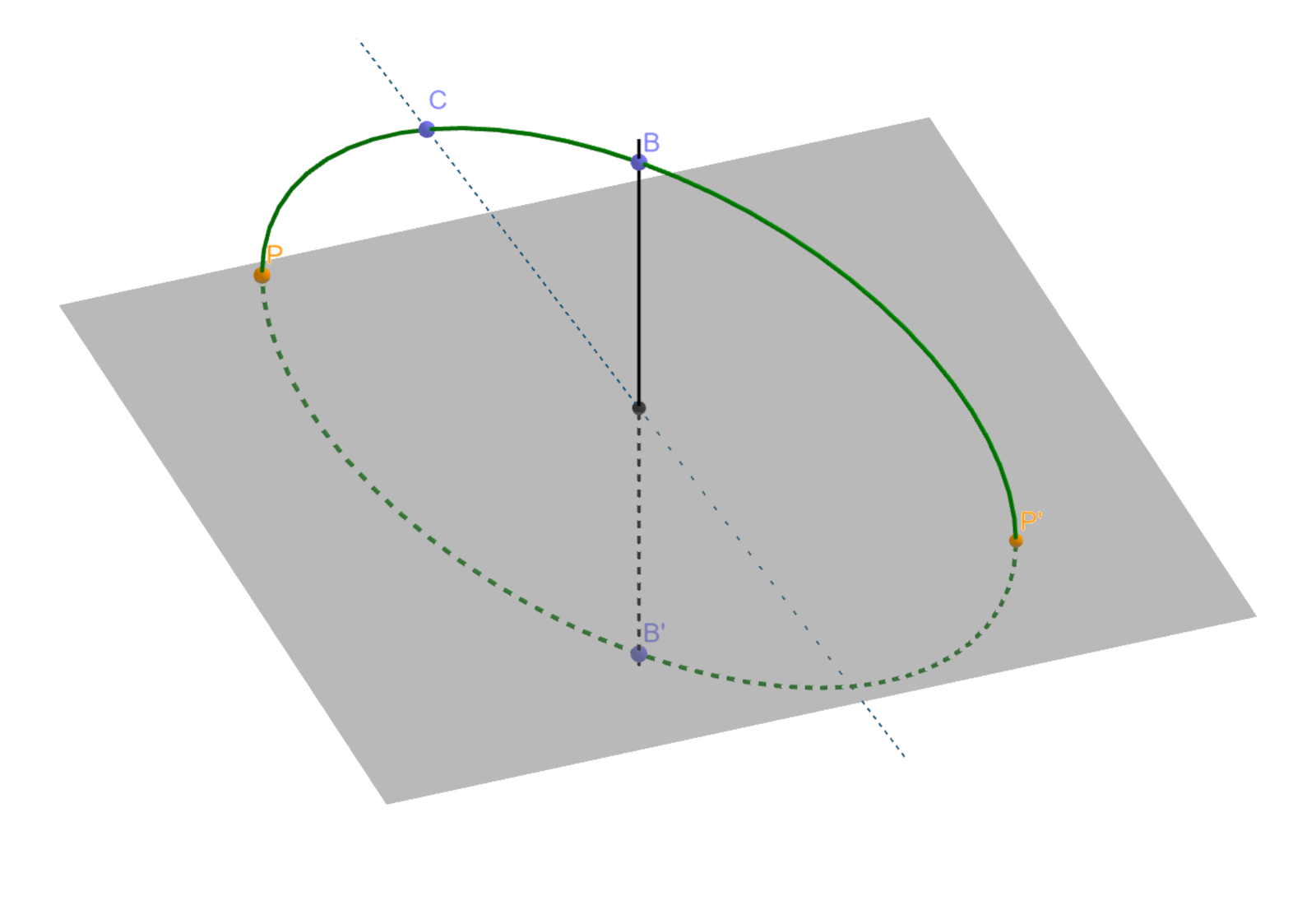
Obracając figurę płaską dookoła prostej , zawartej w tej samej płaszczyźnie, otrzymujemy powierzchnię, która ogranicza figurę, zwaną bryłą obrotową. Prostą nazywamy osią obrotu. Jest ona osią symetrii bryły obrotowej.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0

Film dostępny pod adresem /preview/resource/RObJFJGe1NDma
Animacja pokazuje w jaki sposób wyrabia się naczynia gliniane i jakie figury tworzą takie naczynia.
Przykłady brył obrotowych.


Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0
Przez całą noc padał deszcz i beczka na deszczówkę została napełniona w połowie. Beczka ma wysokość . Jej średnica w najszerszym miejscu wynosi , a w najwęższym .
Ile litrów wody znajduje się w beczce? Przyjmij, że . Skorzystaj z podanego wzoru na pojemność beczki.
Wzór na pojemność beczki:
– pojemność,
– wysokość beczki,
– średnica w najszerszym miejscu,
– średnica w najwęższym miejscu.
Mamy podać pojemność beczki w litrach.
Jeden litr to jeden decymetr sześcienny. Zapisujemy więc wymiary beczki w decymetrach.
Beczka napełniona jest w połowie, zatem obliczamy połowę jej pojemności.
W beczce jest wody.
Bryła powstaje w wyniku obrotu figury wokół prostej .

Film dostępny pod adresem /preview/resource/ROByJb6HnwYFD
Animacja 3d pokazuje, że poprzez obrót prostokąta wzdłuż jego krawędzi otrzymamy walec.
Zaobserwuj, jaka bryła powstaje w wyniku obrotu trójkąta prostokątnego wokół jednej z przyprostokątnych,

Film dostępny pod adresem /preview/resource/RSzO5zNjzr4Q2
Animacja 3d pokazuje, że poprzez obrót trójkąta prostokątnego wzdłuż jego przyprostokątnej otrzymamy stożek.
Nasza planeta nie ma kształtu idealnej kuli. Na skutek ruchu wirowego (czyli ruchu wokół własnej osi) Ziemia uległa spłaszczeniu przy biegunach. W wyniku tego powstała bryła zwana geoidą (z greckiego: gea – Ziemia, eidos – kształt).
Bryłą najbardziej zbliżoną kształtem do Ziemi jest elipsoida obrotowa.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0
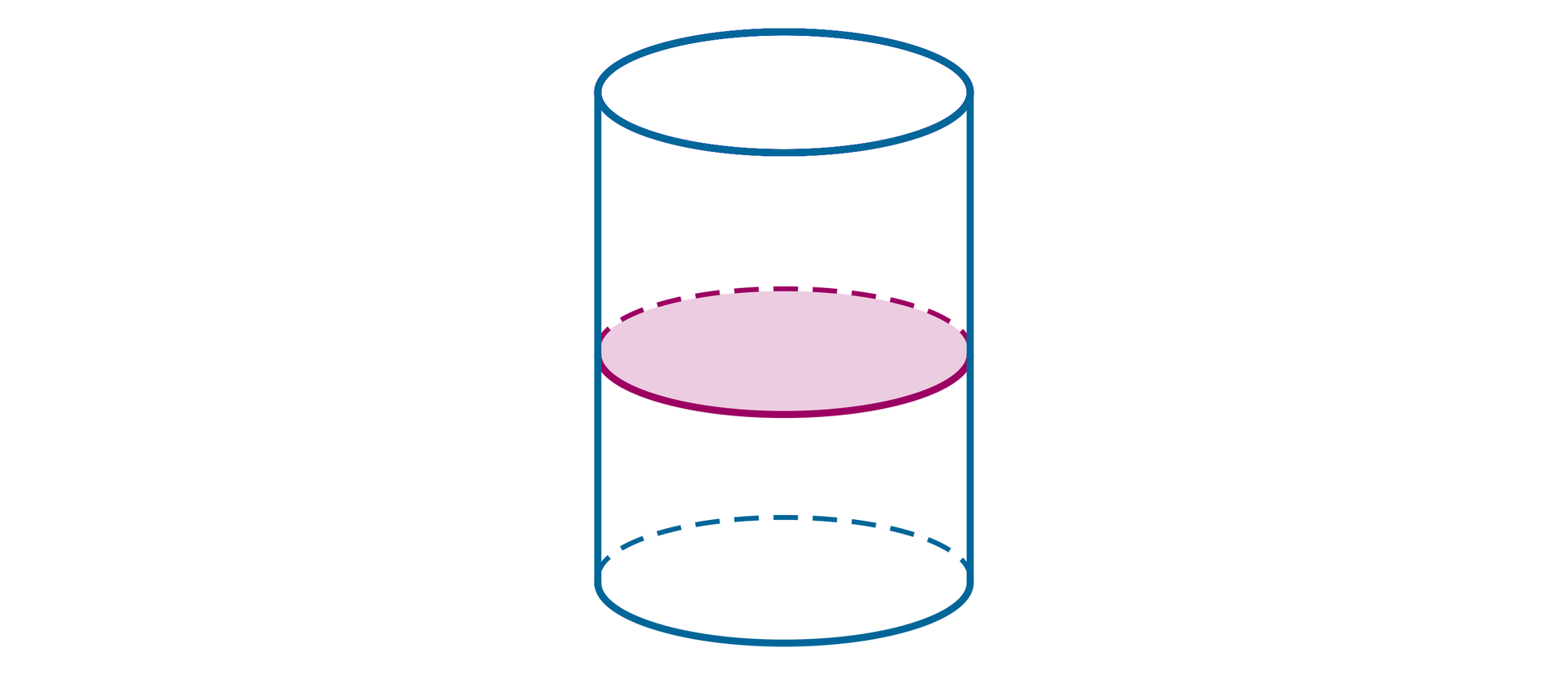
Przekroje brył obrotowych
Figurę płaską, która powstanie po przecięciu bryły płaszczyzną, nazywamy przekrojem tej bryły.
Przekrój osiowy bryły obrotowej to część wspólna tej bryły z płaszczyzną zawierającą oś obrotu.
Przekrój poprzeczny bryły obrotowej to część wspólna tej bryły z płaszczyzną prostopadłą do osi obrotu.
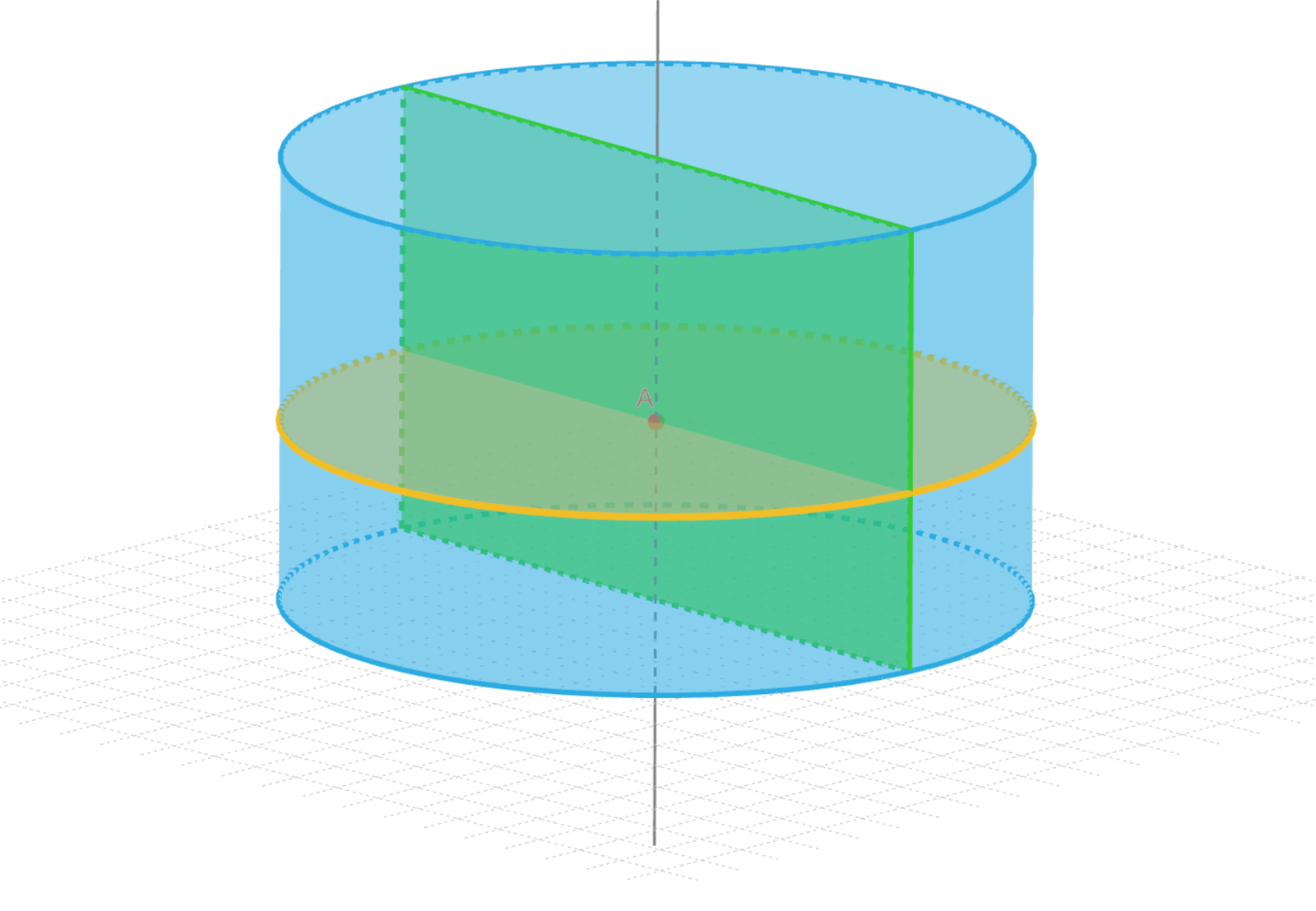
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0
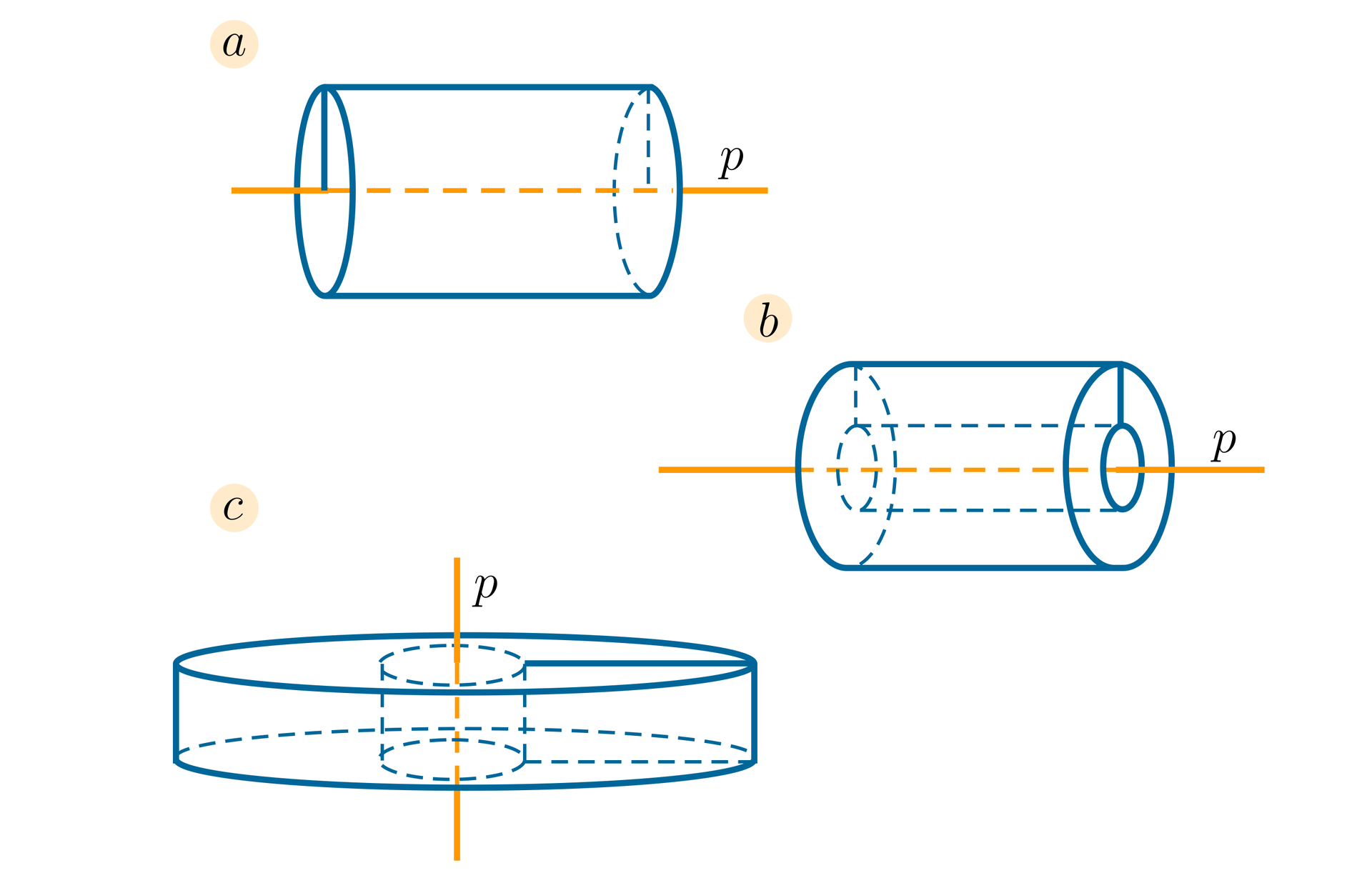
Określ, jaki kształt mają przekroje narysowanych brył. Jeśli nie wiesz, jak nazywa się dana figura, sprawdź w internecie jej nazwę.

Film dostępny pod adresem /preview/resource/RTHF5m3TyZpNt
Animacja 3D pokazuje baterię elektryczną. Kreślone są krawędzie – powstaje walec. Następnie przekroje skośne i poprzeczne dzielą walce na dwie bryły.
Arbuz przekrojono na pół. Otrzymany przekrój jest w kształcie koła o polu . Oblicz średnicę tego koła. Przyjmij .
Korzystamy ze wzoru na pole koła o promieniu .
bo
Obliczamy średnicę koła.
Średnica koła, będąca przekrojem arbuza, jest równa .
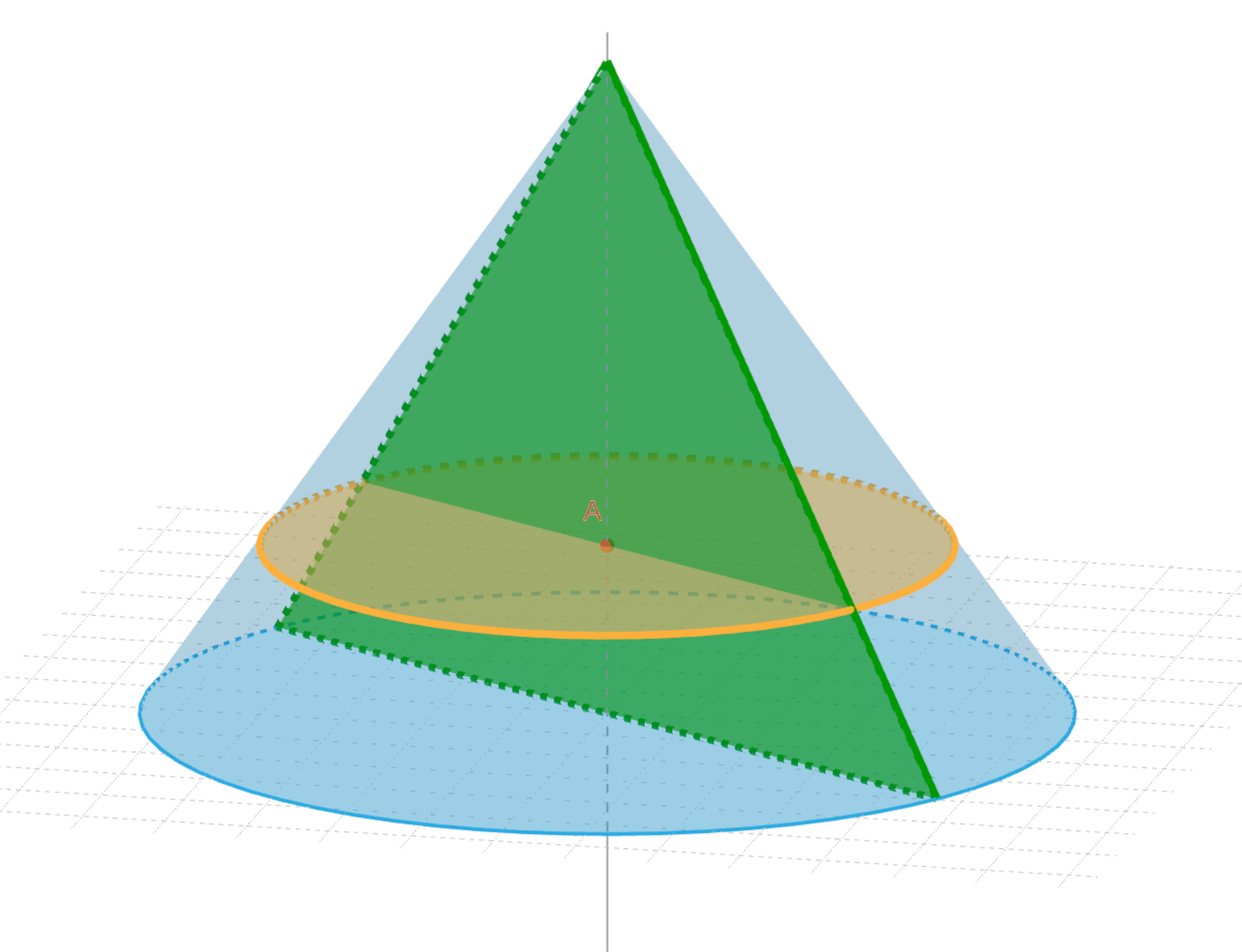
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P118saiJ0
Narysuj bryłę, która powstanie w wyniku obrotu danej figury wokół prostej .
Opisz bryłę, która powstanie w wyniku obrotu danej figury wokół prostej .

Bryła na rysunku powstała w wyniku obrotu pewnej figury płaskiej dookoła prostej.
Narysuj tę figurę i tę prostą.

Naszkicuj przekrój osiowy przedstawionych figur.

Narysuj bryłę obrotową, której przekrój osiowy jest
trójkątem równoramiennym.
trójkątem równobocznym.
Opisz bryłę obrotową, której przekrój osiowy jest
trójkątem równoramiennym.
trójkątem równobocznym.
Narysuj bryłę obrotową, której przekrój osiowy jest
prostokątem,
kwadratem.
Opisz bryłę obrotową, której przekrój osiowy jest
prostokątem,
kwadratem.
Narysuj bryłę obrotową, której przekrój poprzeczny jest kołem.
Opisz bryłę obrotową, której przekrój poprzeczny jest kołem.
- Bryła, której każdy przekrój poprzeczny jest kołem, jest bryłą obrotową.
- Sześcian jest bryłą obrotową.
- Istnieje bryła obrotowa, której przekrój osiowy jest inny niż przekrój poprzeczny.
Narysuj bryłę obrotową powstałą w wyniku obrotu
trapezu prostokątnego wokół krótszego ramienia,
trapezu równoramiennego wokół dłuższej podstawy.
Opisz bryłę obrotową powstałą w wyniku obrotu
trapezu prostokątnego wokół krótszego ramienia,
trapezu równoramiennego wokół dłuższej podstawy.
Narysuj bryłę, która powstała w wyniku obrotu prostokąta wokół prostej
na której leży jeden z boków,
równoległej do dłuższego boku, która leży poza tym bokiem,
równoległej do krótszego boku, która leży poza tym bokiem.
Opisz bryłę, która powstała w wyniku obrotu prostokąta wokół prostej
na której leży jeden z boków,
równoległej do dłuższego boku, która leży poza tym bokiem,
równoległej do krótszego boku, która leży poza tym bokiem.