Definicje i twierdzenia z wielokątów, kół i okręgów, brył oraz potęg o podstawach wymiernych
W tym materiale zawarte są definicje oraz twierdzenia dotyczące wielokątów, kół i okręgów, brył oraz potęg o podstawach wymiernych.
Potęgą o wykładniku naturalnym nazywamy iloczyn czynników, z których każdy jest równy .
Przyjmujemy, że dla oraz .
Iloczyn potęg o tych samych podstawach
Dla dowolnej liczby rzeczywistej i dowolnych liczb naturalnych i prawdziwa jest równość

Film dostępny pod adresem /preview/resource/R1Z1tjwk482bF
Animacja przedstawia w jaki sposób mnożymy potęgi o takich samych podstawach.
Na przykład:
Iloraz potęg o tych samych podstawach
Dla dowolnej liczby rzeczywistej i dowolnych liczb naturalnych i spełniających warunek prawdziwa jest równość

Film dostępny pod adresem /preview/resource/R1HUeWq4VRmFi
Animacja przedstawia w jaki sposób dzielimy potęgi o takich samych podstawach.
Na przykład:
Potęga potęgi
Dla dowolnej liczby rzeczywistej i dowolnych liczb naturalnych i prawdziwa jest równość

Film dostępny pod adresem /preview/resource/RDBoa22Rshi5M
Animacja przedstawia w jaki sposób potęgujemy potęgę.
Na przykład:
Iloczyn potęg o tych samych wykładnikach
Dla dowolnych liczb rzeczywistych i i dowolnej liczby naturalnej prawdziwa jest równość

Film dostępny pod adresem /preview/resource/RGkqhPYvk1uXR
Animacja przedstawia w jaki sposób potęgujemy iloczyn liczb.
Na przykład:
Iloraz potęg o tych samych wykładnikach
Dla dowolnych liczb rzeczywistych i i dowolnej liczby naturalnej prawdziwa jest równość

Film dostępny pod adresem /preview/resource/RS6b7c3hacr1S
Animacja przedstawia w jaki sposób potęgujemy iloraz liczb.
Na przykład:
Kołem o środku w punkcie i promieniu r nazywamy zbiór tych punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa .

– koło o środku w punkcie i promieniu
Wycinkiem koła (wycinkiem kołowym) nazywamy część tego koła ograniczoną łukiem i ramionami kąta środkowego.

Odcinkiem koła (odcinkiem kołowym) nazywamy część koła odciętą przez cięciwę wraz z tą cięciwą.

Każda cięciwa wyznacza dwa odcinki koła. Średnica dzieli koło na dwa półkola.
Obracając figurę płaską dookoła prostej , zawartej w tej samej płaszczyźnie, otrzymujemy powierzchnię, która ogranicza figurę, zwaną bryłą obrotową. Prostą nazywamy osią obrotu. Jest ona osią symetrii bryły obrotowej.
Kula to zbiór wszystkich punktów przestrzeni, których odległość od punktu, zwanego środkiem, jest nie większa od długości odcinka, zwanego promieniem kuli.

Sfera to zbiór wszystkich punktów przestrzeni, których odległość od punktu, zwanego środkiem, jest równa długości odcinka, zwanego promieniem sfery.

Cięciwa sfery (kuli) to odcinek o końcach leżących na sferze. Cięciwa przechodząca przez środek sfery (kuli), to średnica

Walec to bryła, która powstała w wyniku obrotu prostokąta dookoła prostej zawierającej jeden z boków tego prostokąta.
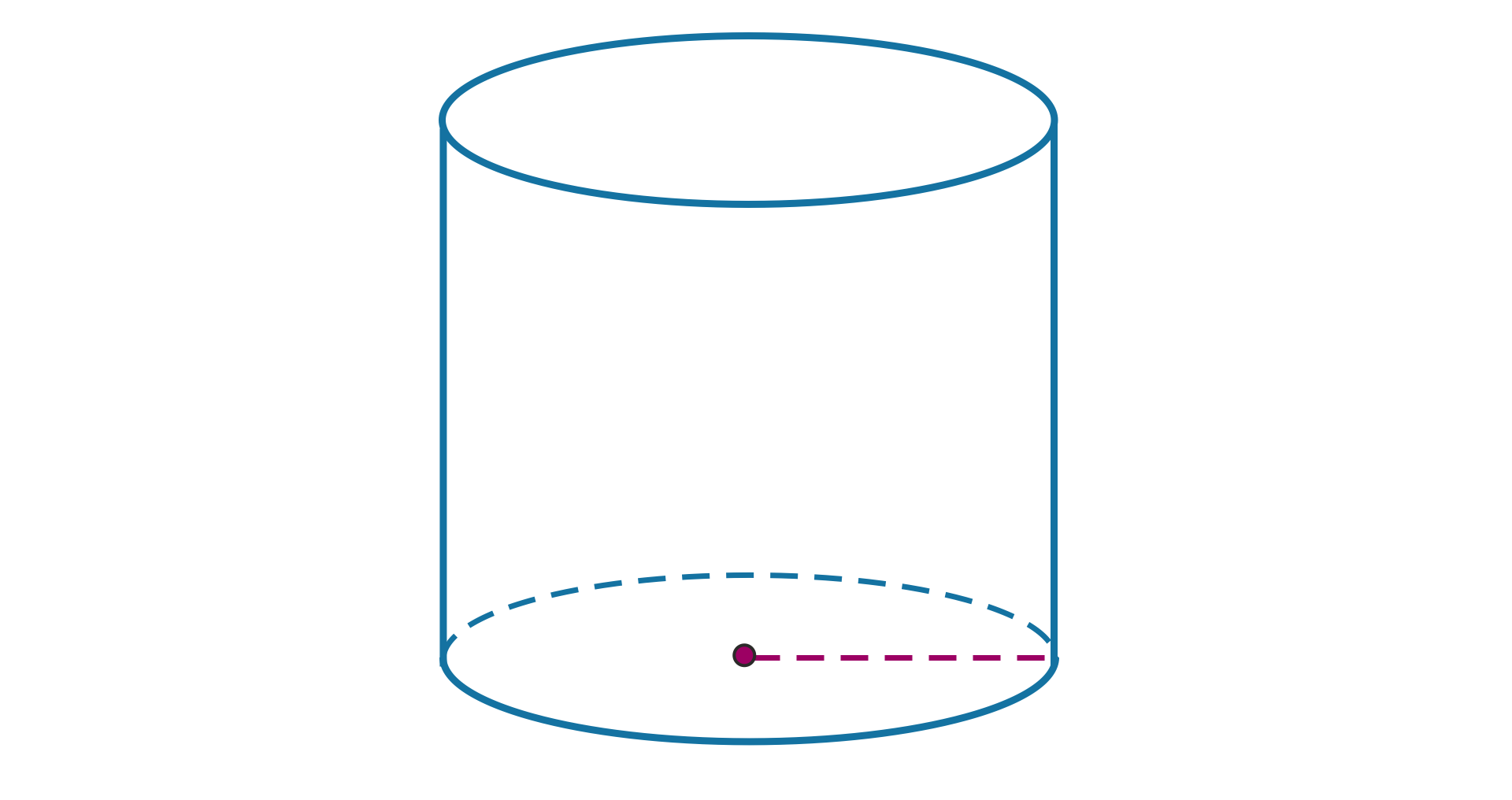

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PDzUMGLYw
Stożek to bryła, która powstała w wyniku obrotu trójkąta prostokątnego dookoła prostej zawierającej jedną z przyprostokątnych.
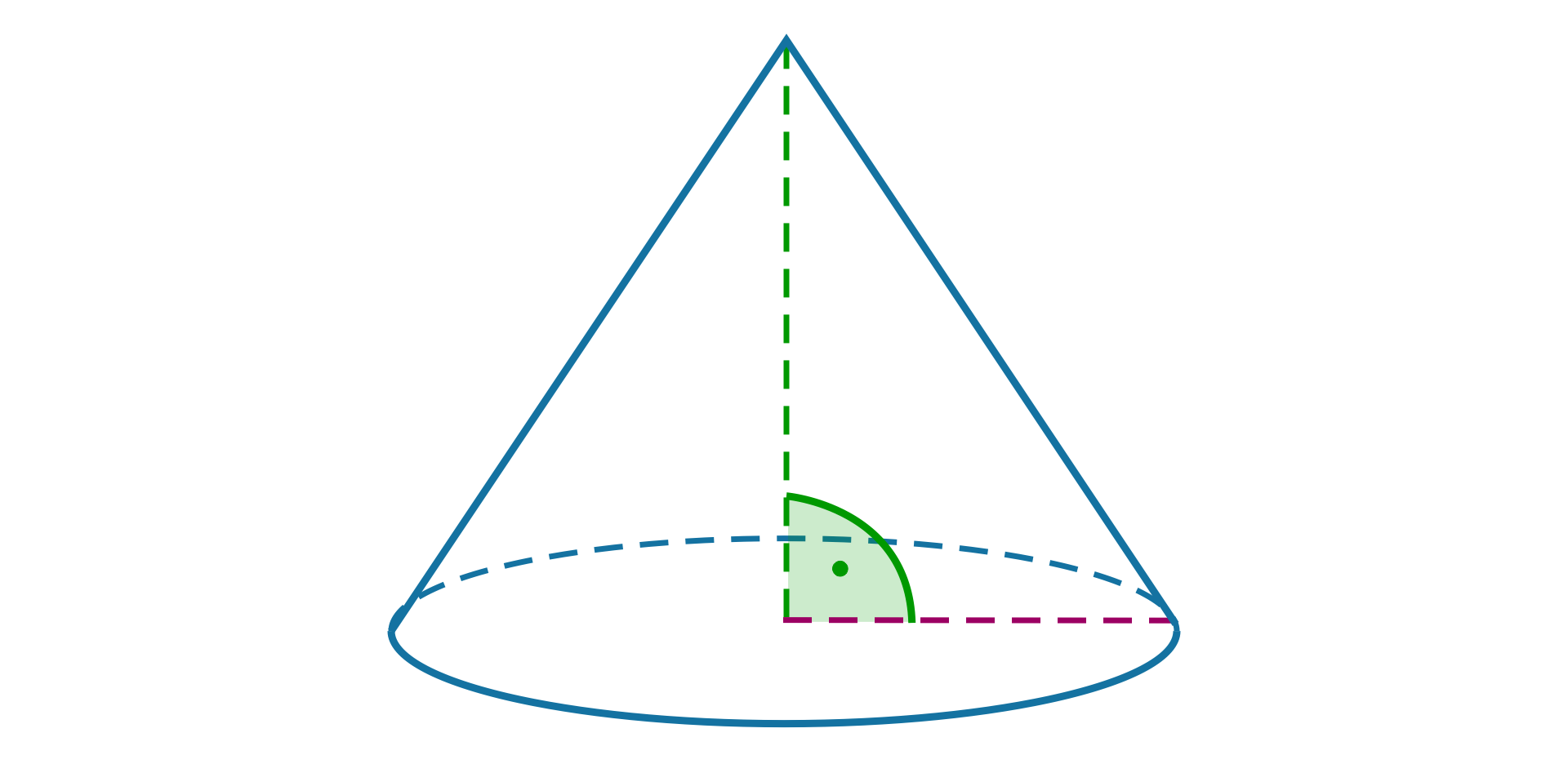

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PDzUMGLYw
Graniastosłup to figura przestrzenna, która ma
dwie podstawy będące przystającymi wielokątami,które leżą w płaszczyznach równoległych.
ściany boczne będące równoległobokami.
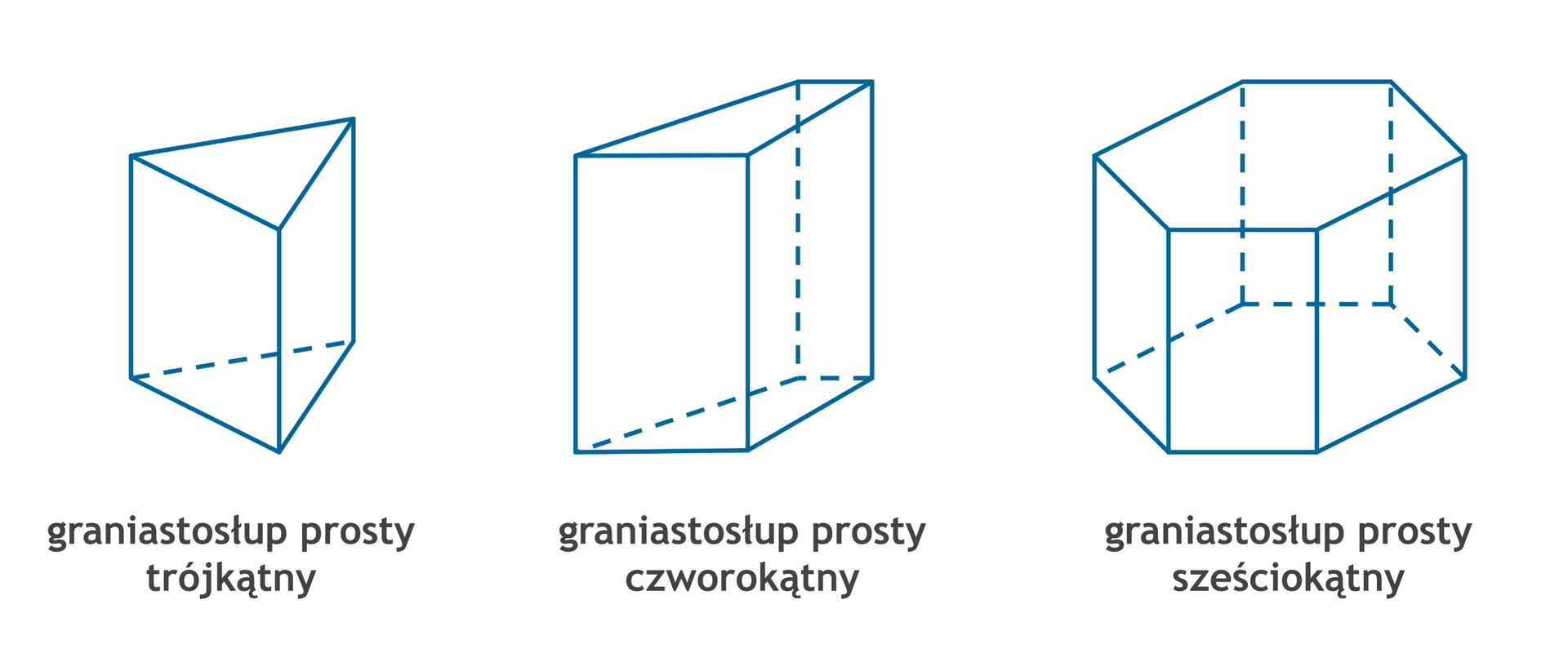
Graniastosłup prosty to figura przestrzenna, która ma
dwie podstawy będące przystającymi (jednakowymi) wielokątami,
ściany boczne będące prostokątami.
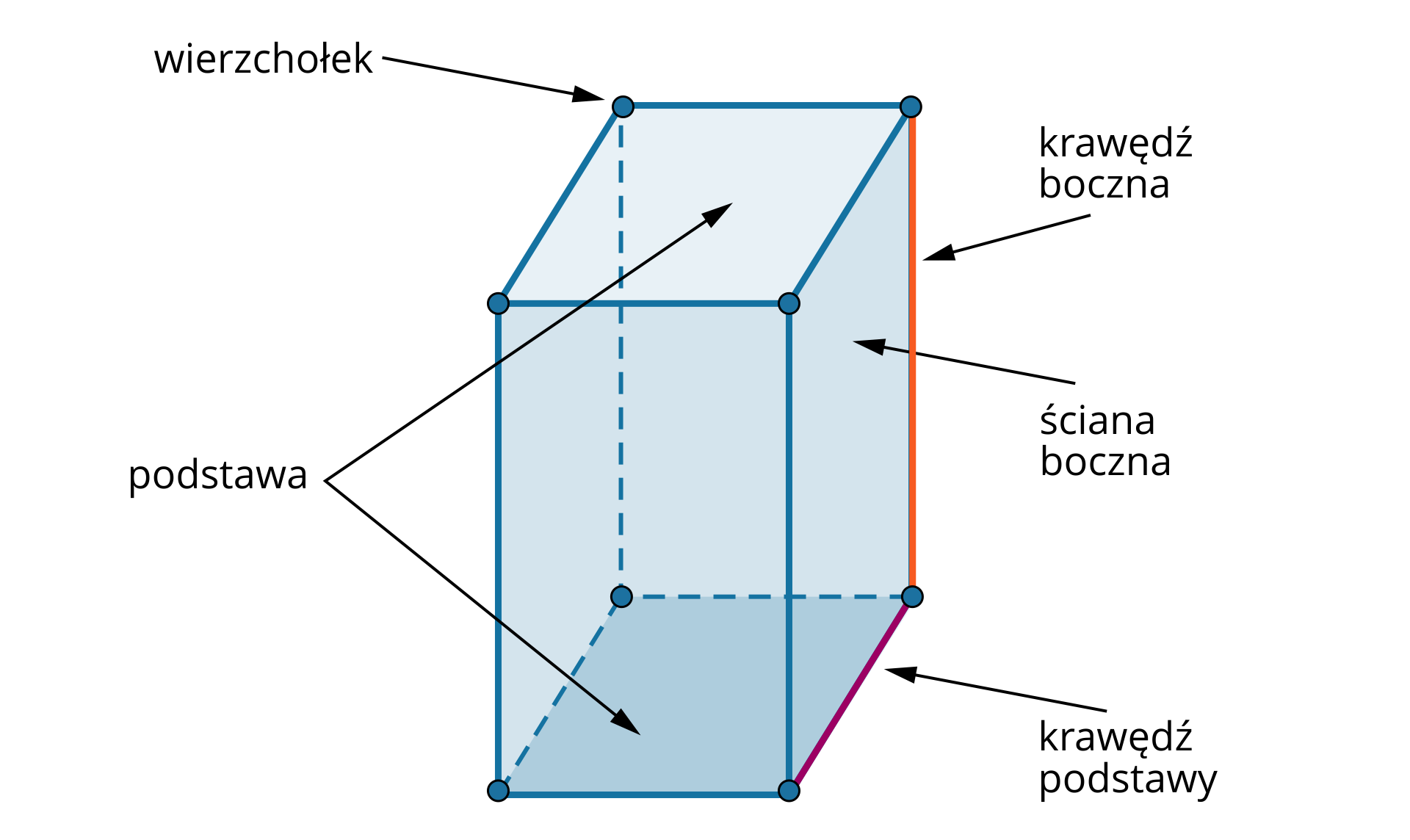
Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.
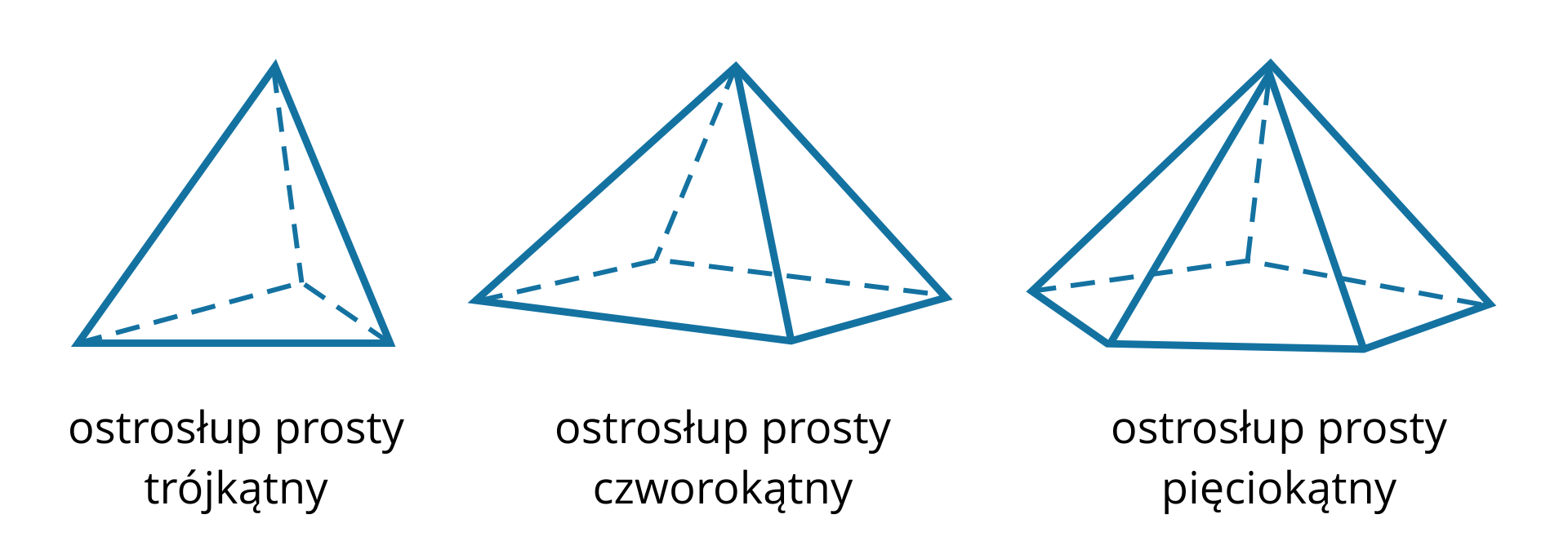
Ostrosłup to figura przestrzenna, która ma podstawę w kształcie wielokąta, a jej ściany boczne są trójkątami.
Jest to ostrosłup, który ma wszystkie krawędzie boczne równej długości.
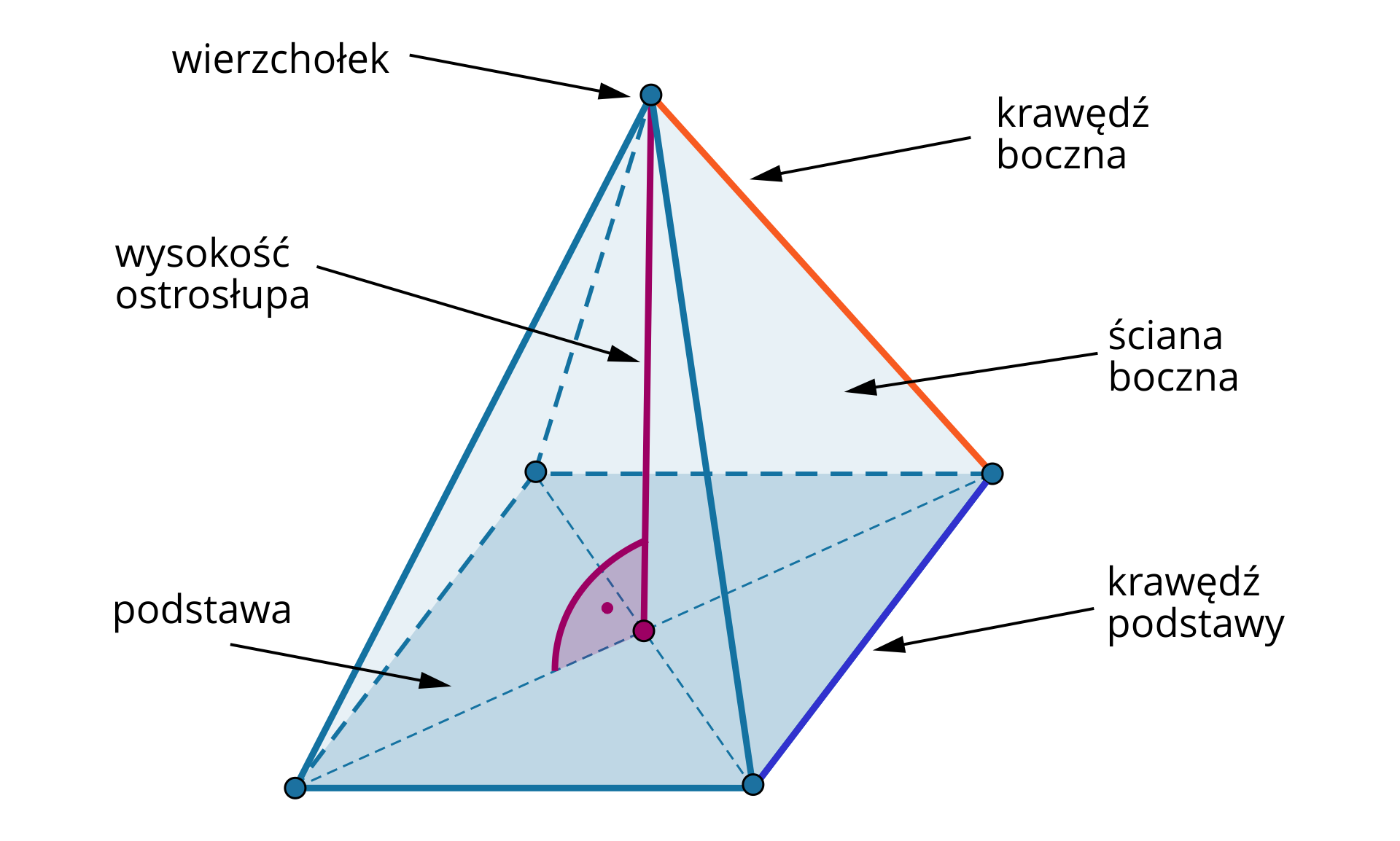
Nazwa ostrosłupa zależy od rodzaju wielokąta w podstawie.