Dlaczego jądro jest trwałe – deficyt masy i energia wiązania
Co wiąże nukleony w jądrze? Jaka energia jest potrzebna, aby rozbić jądro na mniejsze fragmenty? Jednym z elementów szczególnej teorii względności ogłoszonej przez Alberta EinsteinaAlberta Einsteina w r. była równoważność masy i energii. Jego odkrycie pozwoliło wyjaśnić pochodzenie energii wiązania – energii łączącej składniki jądra atomowego w jedną spójną strukturę. Jeśli chcesz poznać podstawowe prawa rządzące materią i masą na poziomie atomowym, to znalazłeś się we właściwym miejscu.

założenia budowy modelu atomu według Bohra;
podstawowe oddziaływania, które zachodzą między nukleonami;
definicję liczby masowej i atomowej (porządkowej);
definicję izotopu oraz jak odróżnić izotopy na podstawie liczby masowej i atomowej (porządkowej);
jak podać skład jądra na podstawie znajomości liczby masowej i porządkowej ;
przykłady samorzutnego rozpadu niestabilnych jąder atomowych oraz zapis schematów takich rozpadów za pomocą zasady zachowania ładunku i zasady zachowania liczby nukleonów.
podawać definicję deficytu masy i wymieniać warunek jego występowania;
zapisywać warunek równoważności masy i energii ;
podawać definicję energii wiązania jądra atomowego;
obliczać wartość energii wiązania jądra i energii wiązania przypadającej na jeden nukleon dla dowolnego pierwiastka.
Energia wiązania
Świat zna Alberta EinsteinaAlberta Einsteina głównie dzięki wzorowi , który okazał się sztandarowym przykładem nowego sposobu postrzegania rzeczywiści przez fizykę współczesną. Wzór ten stwierdza równoważność masy i energii. Zmiana masy układu może zachodzić wskutek wymiany nie tylko substancji z otoczeniem, lecz także energii. Masa i energia stały się jakościowo różnymi postaciami materii.
Jeśli znamy masę protonu i neutronu oraz wiemy, że atom składa się z protonów i neutronów , to możemy obliczyć masę jądra atomu. W tym celu korzystamy ze wzoru:
Okazuje się jednak, że wzór ten daje niezgodne wyniki w porównaniu z danymi eksperymentalnymi. Masa jądra jest bowiem zawsze mniejsza niż suma mas jego poszczególnych składników (nukleonów).
Ten ubytek masy, czy też deficyt masydeficyt masy, obliczamy według wzoru:
,
gdzie to rzeczywista masa jądra danego pierwiastka.
Ubytek masy związany jest z oddziaływaniami jądrowymi i energią potrzebną do utrzymania jądra atomowego w całości. Podczas powstawania jądra energia związana z ubytkiem masy została zamieniona na inną formę energii równą .
Obliczmy zatem energię wiązania dla jąder atomowych. Weźmy pod uwagę jądro helu. Składa się ono z nukleonów: dwóch protonów i dwóch neutronów.
Masa protonu:
Masa neutronu:
Masa jądra helu:
Deficyt masy:
Czyli:
Jak widać, deficyt masy stanowi zaledwie drobny ułamek masy czterech nukleonów – około .
Deficytowi masy tej wielkości odpowiada równoważna mu energia obliczona z zależności .
Skoro , to:
Energię tę nazywamy energią wiązania jądra danego atomu.
deuter | |||||
hel | |||||
lit | |||||
węgiel | |||||
tlen | |||||
uran |
W fizyce obowiązuje międzynarodowy układ jednostek (SISI), w którym jednostką energii jest jeden dżul . Jednak jednostka ta jest czasami zbyt duża, a czasami – zbyt mała. Przykładowo: gdyby energia elektryczna zużywana w gospodarstwie domowym była wyrażana w dżulach, musielibyśmy operować ogromnymi liczbami sięgającymi setek milionów. Z tego powodu używamy jednostki energii elektrycznej zwanej kilowatogodzinąkilowatogodziną (poznaliście ją już w gimnazjum) – . Jest ona równa .
W świecie atomów i cząstek elementarnych energia jednego dżula jest energią gigantyczną. Z obliczeń wynika (patrz wyżej), że energia wiązania jąder atomów jest równa w odniesieniu do małych jąder około jednej bilionowej dżula, a dla najcięższych jąder – jednej dziesięciomiliardowej dżula. Energia atomu wodoru na poziomie podstawowym wynosi . Z tych powodów fizycy używają jednostki energii zwanej elektronowoltemelektronowoltem.
Jeden elektronowolt jest jednostką energii, która jest równoważna pracy wykonywanej przez siły elektryczne, kiedy przemieszczają elektron w polu elektrostatycznym między dwoma punktami, pomiędzy którymi panuje napięcie elektryczne . Odpowiada to w przybliżeniu wartości . Pracę tę można wyrazić w dżulach, ale wygodniej jest to zrobić w elektronowoltach lub też posłużyć się wielokrotnościami tej jednostki: kiloelektronowoltem , megaelektronowoltem lub gigaelektronowoltem
Mnożnik | Nazwa | Symbol |
|---|---|---|
elektronowolt | ||
kiloelektronowolt | ||
megaelektronowolt | ||
gigaelektronowolt | ||
teraelektronowolt |
Współczesne urządzenia do badania cząstek rozpędzają je do energii ponad (gigaelektronowoltów, czyli ), a Wielki Zderzacz HadronówWielki Zderzacz Hadronów (największa maszyna świata) uzyskuje energię cząstek rzędu kilku , czyli kilku bilionów elektronowoltów. Energie wyrażone w elektronowoltach wydają się być gigantyczne, ale są to tak naprawdę wartości mniejsze niż jedna milionowa dżula. Należy jednak pamiętać, że energiami tymi obdarzone są cząstki o masach rzędu (w spoczynku).
Wróćmy teraz do wartości liczbowych zawartych w tabeli energii wiązania wybranych pierwiastków. Dane te można przedstawić graficznie na wykresie zależności energii wiązania jądra od liczby masowej (wykres zawiera dane większej liczby pierwiastków niż w tabelce).

Na podstawie danych z tabeli można zauważyć, że energia wiązania jest tym większa, im większa jest liczba nukleonów w jądrze. Jest to zrozumiałe – większa liczba protonów oznacza większe siły odpychania, zatem jądro może być stabilne, pod warunkiem że energia wiązania będzie większa. Właśnie dlatego ciężkie jądra mają duży nadmiar neutronów.
Ponowna analiza danych umieszczonych w tabeli prowadzi do jeszcze jednego ciekawego wniosku: Energia wiązania każdego nukleonu w jądrze helu jest większa niż energia wiązania takiego nukleonu w jądrze litu. Z wykresu wynika, że energia wiązania rośnie wraz ze wzrostem liczby masowej, ale nie jest to wzrost liniowy (wzrost energii wiązania jest coraz wolniejszy).
Czym jest energia wiązania przypadająca na jeden nukleon? Jest to ilość energii, jaką trzeba dostarczyć do jądra, aby wyrwać z niego jeden nukleon. Jeżeli chcemy zamiast jądra uzyskać niezależne cząstki swobodne, to musimy w tym celu dostarczyć energię równą całkowitej energii wiązania.
Ciekawy wynik otrzymamy, gdy na wykresie przedstawimy zależność energii wiązania przypadającej na jeden nukleon od liczby masowej – liczby nukleonów.
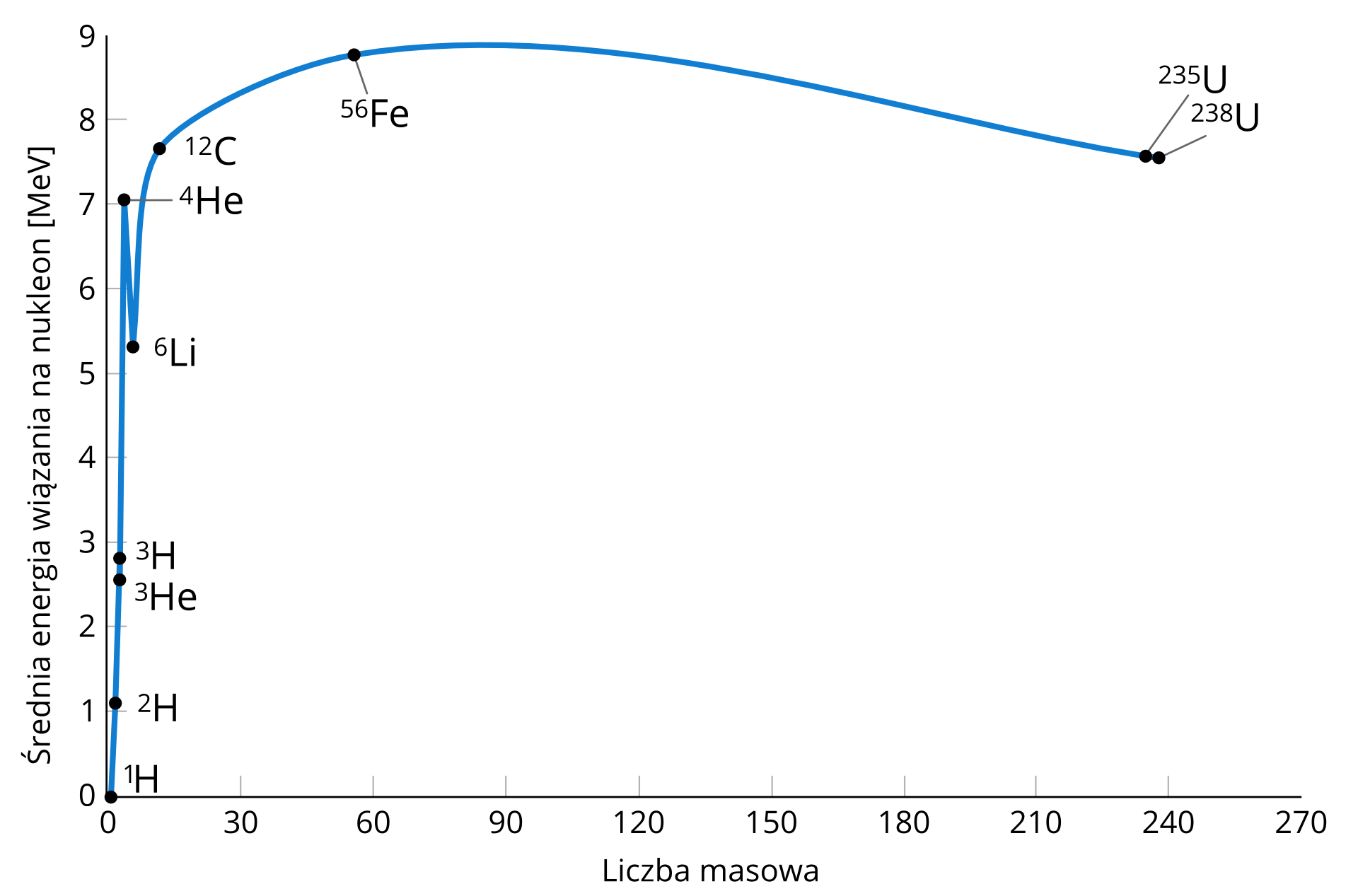
Analiza wykresu pozwala stwierdzić, że największa średnia energia wiązania przypada na jądra znajdujące się w środkowej części wykresu. W porównaniu z tymi jądrami zarówno jądra najlżejsze (zaczynając od deuteru, helu czy węgla), jak i te cięższe (takie jak uran) mają mniejszą energię przypadającą na jeden nukleon.
Najbardziej trwałe są jądra leżące w środkowej części wykresu zależności energii wiązania jądra od liczby masowej.
Maksymalną wartość energii wiązania ma żelazo – na nukleon. Jest to tylko jeden z wniosków wynikających z przebiegu tego wykresu.
Warto też zwrócić uwagę na fakt dużej, w porównaniu z sąsiednimi jądrami, energii wiązania na nukleon jądra helu . Lit, który ma większą energię wiązania i większą masę, ma mniejszą energię przypadającą na jeden nukleon. Oznacza to, że jądro helu jest związane silniej niż jądra o mniejszej i nieco większej masie. Z tego wynikają istnienie cząstki i przekonanie (żywione długo przez Rutherforda), że w jądrach atomów takie cząstki istnieją cały czas. Obszary wykresu dotyczące zarówno mniejszych, jak i większych liczb masowych spowodowały prawdziwą rewolucję. Dzięki niemu możliwa stała się produkcja energii jądrowej na dwa sposoby (ale również możliwość zbudowania dwóch rodzajów bomb jądrowych). Ponadto za pomocą tego wykresu wyjaśniono, co jest źródłem energii gwiazd, a także wytłumaczono, jak tworzyły się pierwiastki podczas powstania i ewolucji Wszechświata. Tymi kwestiami zajmiemy się na najbliższych lekcjach.
Podsumowanie
Masa i energia całkowita są miarą tej samej wielkości fizycznej. Zmiana masy układu może zachodzić wskutek wymiany nie tylko substancji, lecz także energii.
Równoważność masy i energii Albert Einstein opisał za pomocą wzoru:
,gdzie:
– masa ciała, – prędkość światła w próżni.Masa jądra jest mniejsza od sumy mas nukleonów, z którego jest ono utworzone. Tę różnicę nazywamy deficytem masy.
Energia wiązania jest równa wartości pracy, którą należy wykonać, aby układ rozłożyć na pojedyncze cząstki (w przypadku jądra – są to nukleony).
Energia wiązania jest równa wartości energii związanej z deficytem masy :
,
gdzie: – prędkość światła w próżni.Energia wiązania zmienia się wraz liczbą nukleonów w jądrze; im większa liczba nukleonów, tym jądro jest silniej związane.
Charakterystyczną wielkością dla danego jądra jest energia wiązania przypadająca na jeden nukleon w jądrze. Jest to energia, jaką trzeba dostarczyć do jądra, aby uwolnić z niego jeden nukleon.
Zadania podsumowujące
Które informacje są prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Im większa energia wiązania przypadająca na jeden nukleon , tym więcej energii potrzeba, aby rozbić takie jądro. | □ | □ |
| Defektowi masy odpowiada równoważna mu energia | □ | □ |
| Gdyby porównać masę jądra atomowego z sumą mas jego składników, wówczas okaże się, że jądro jako układ nukleonów związanych siłami jądrowymi jest cięższy niż suma mas tych nukleonów. | □ | □ |
Uzupełnij lukę.
zerowa, najmniejsza, największa
Jądra, które są stabilne to właśnie te, w których energia wiązania przypadająca na jeden nukleon jest .......................
Słownik
energia cząstki pozostającej w spoczynku względem inercjalnego układu odniesienia.
różnica między masą cząstek swobodnych a masą jądra utworzonego z tych cząstek.
jednostka energii równoważna pracy, jaką wykonują siły elektryczne, kiedy przemieszczają elektron w polu elektrostatycznym między dwoma punktami, pomiędzy którymi panuje napięcie . Odpowiada to w przybliżeniu wartości .
energia równoważna deficytowi masy. Odpowiada pracy, którą należy wykonać, aby podzielić jądro na pojedyncze nukleony. Wartość energii wiązania jądra równa jest energii uzyskanej kosztem różnicy masy między nukleonami swobodnymi a nukleonami związanymi w jądrze atomu.
jednostka energii równoważna ilości energii zużywanej przez urządzenie o mocy .
stała masa charakteryzująca ciało niezależnie od rozpatrywanego układu odniesienia, w którym to ciało spoczywa.
Międzynarodowy Układ Jednostek Miar (Système international d'unités), używany w Polsce od r.
energia wiązania jądra podzielona przez liczbę wszystkich nukleonów w jądrze danego pierwiastka; inaczej: energia wiązania przypadająca na jeden nukleon lub właściwa energia wiązania.
największy na świecie akcelerator (przyspieszacz) cząstek, znajdujący w CERN‑ie (Europejski Ośrodek Badań Jądrowych) pod Genewą.
Biogram

Albert Einstein
[albert ajnsztajn]
Jeden z najwybitniejszych fizyków teoretyków wszech czasów, twórca szczególnej ( r.) i ogólnej teorii względności ( r.). Laureat Nagrody Nobla w dziedzinie fizyki ( r.).