Długość okręgu
Czy wiesz, jaką długość ma okrąg o danym promieniu? Oczywistym jest, że im dłuższy jest promień okręgu, tym większa jest długość okręgu. Jeżeli rozetniemy okrąg i „wyprostujemy” tą krzywą to otrzymamy odcinek, którego długość jest równa długości okręgu.
To „wyprostowanie” okręgu nazywa się rektyfikacją i polega na skonstruowaniu odcinka, którego długość jest równa obwodowi danego okręgu. Już bardzo dawno temu uczeni poszukiwali wzoru pozwalającego obliczyć długość okręgu. Zauważyli oni, że stosunek długości okręgu do długości średnicy jest dla dowolnego okręgu zawsze taki sam.
W tym materiale będziesz korzystać ze wzoru na długość okręgu w rozwiązywaniu problemów teoretycznych i praktycznych.
Okrąg
Film dostępny pod adresem /preview/resource/R1ZWWaC0z6ZjA
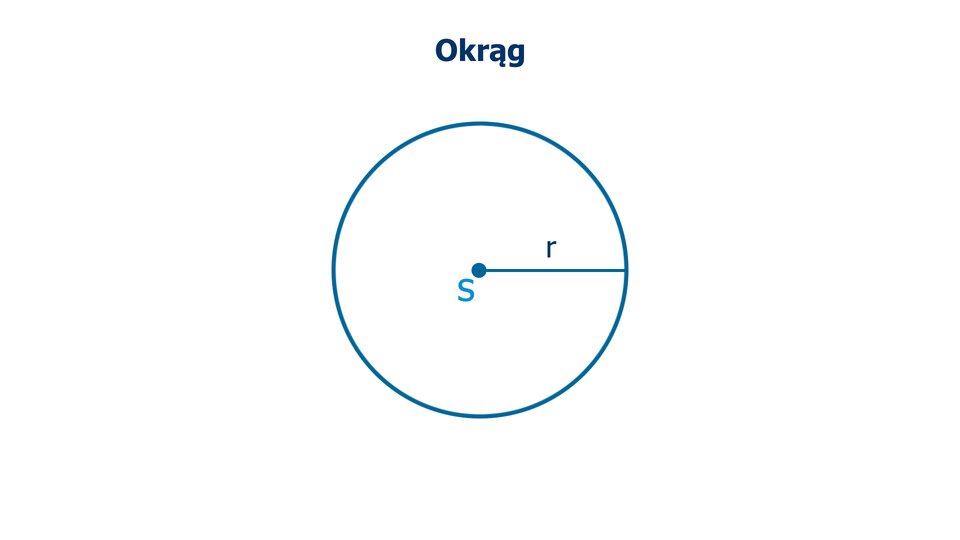
Animacja pokazuje, czym jest okrąg.
Okręgiem o środku w punkcie i promieniu nazywamy zbiór wszystkich punktów płaszczyzny, których odległość od punktu jest równa .
Okrąg o środku w punkcie i promieniu oznaczamy .

Długość okręgu
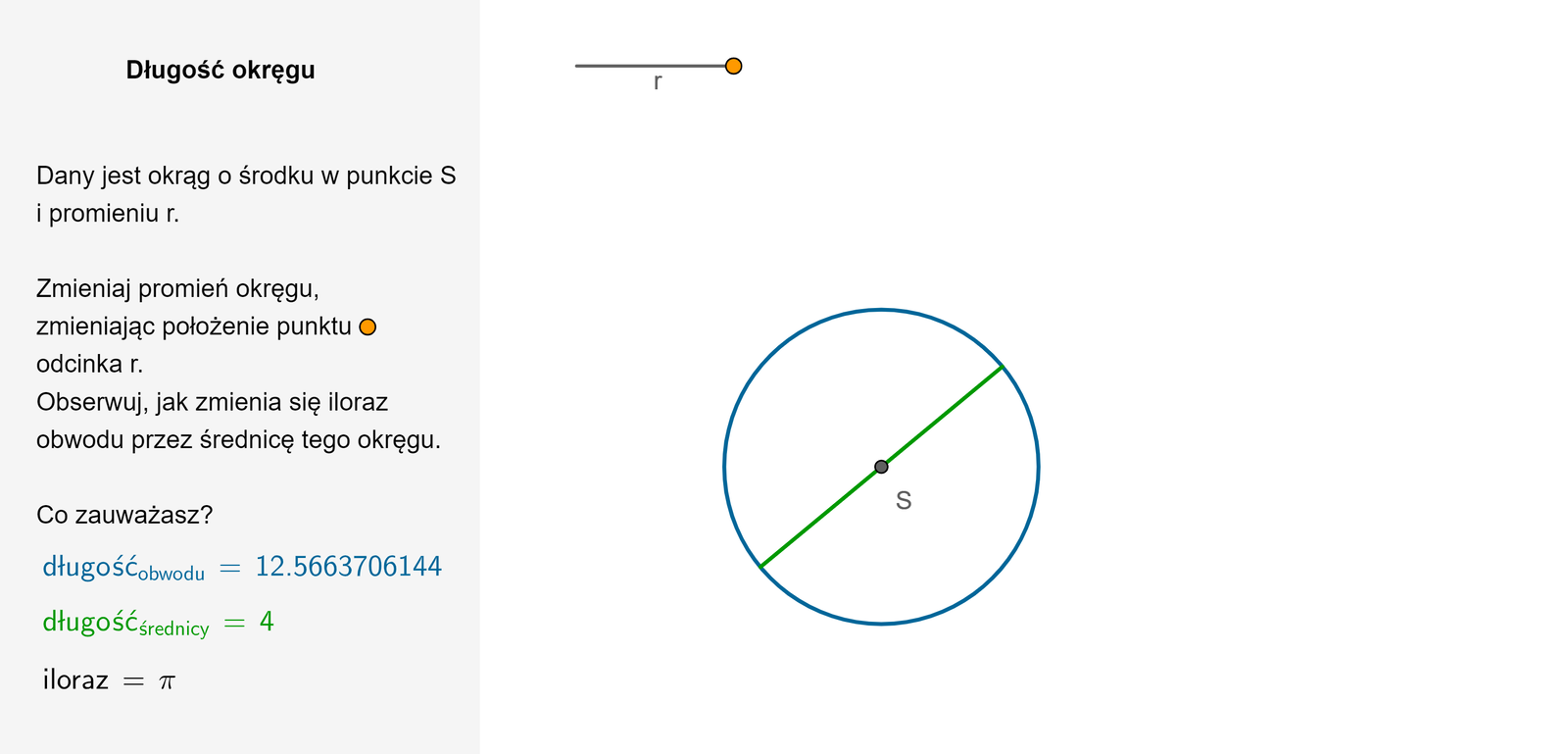
Przez wiele stuleci uczeni poszukiwali wzoru pozwalającego określić długość okręgu, którego promień jest znany. Dokonując przybliżonych pomiarów, zauważyli, że stosunek długości okręgu do jego średnicy jest w każdym przypadku w przybliżeniu równy .
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższego apletu.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DmQwgAlcy
Przeprowadzony eksperyment pozwolił na znalezienie dokładniejszej liczby określającej stosunek długości okręgu do jego średnicy.
Liczbę tę w w. oznaczono grecką literą od pierwszej litery greckiego słowa perimetron, czyli obwód.
Oznaczmy:
– długość okręgu,
– promień okręgu.
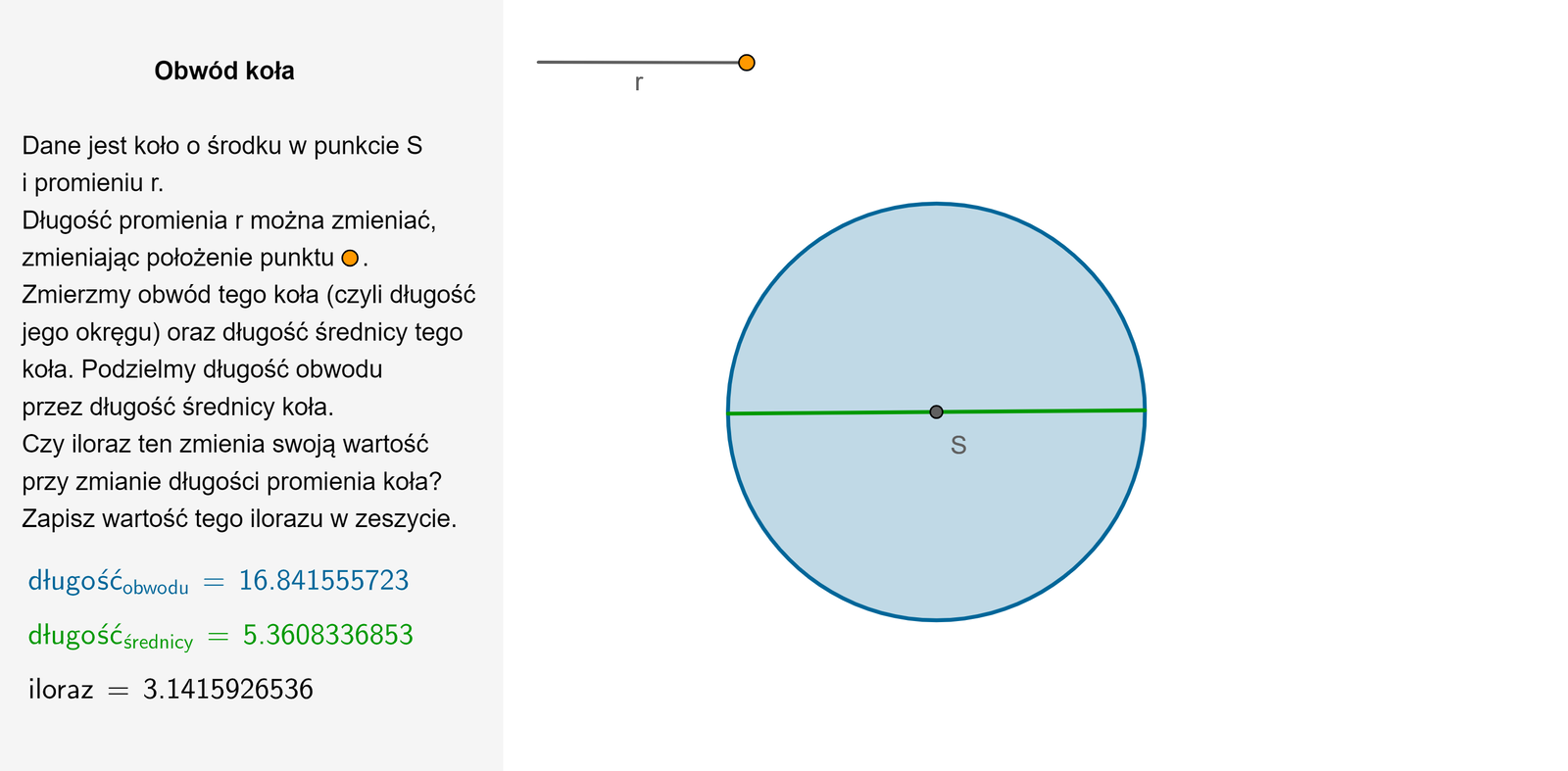
Wtedy średnica okręgu jest równa oraz
Długość okręgu o promieniu wyraża się wzorem .
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższego apletu.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DmQwgAlcy
Liczba
Starożytni Egipcjanie przyjmowali, że stosunek obwodu koła do jego średnicy jest równy
Średniowieczni Chińczycy uważali, że jest on równy
Przez wieki podawano coraz lepsze przybliżenie liczby .
W w. matematyk holenderski Ludolph van Ceulen [Ludolf fan keule] podał jej wartość z dokładnością do miejsc po przecinku:
Na cześć tego matematyka liczba pi zwana jest też ludolfiną.
W w. udowodniono, że liczba nie jest liczbą wymierną. Nie da się jej zatem zapisać w postaci ułamka dziesiętnego skończonego, ani w postaci ułamka dziesiętnego nieskończonego okresowego.
Obecnie znamy przybliżenie liczby z dokładnością do kilku bilionów miejsc po przecinku.
Rektyfikacja koła
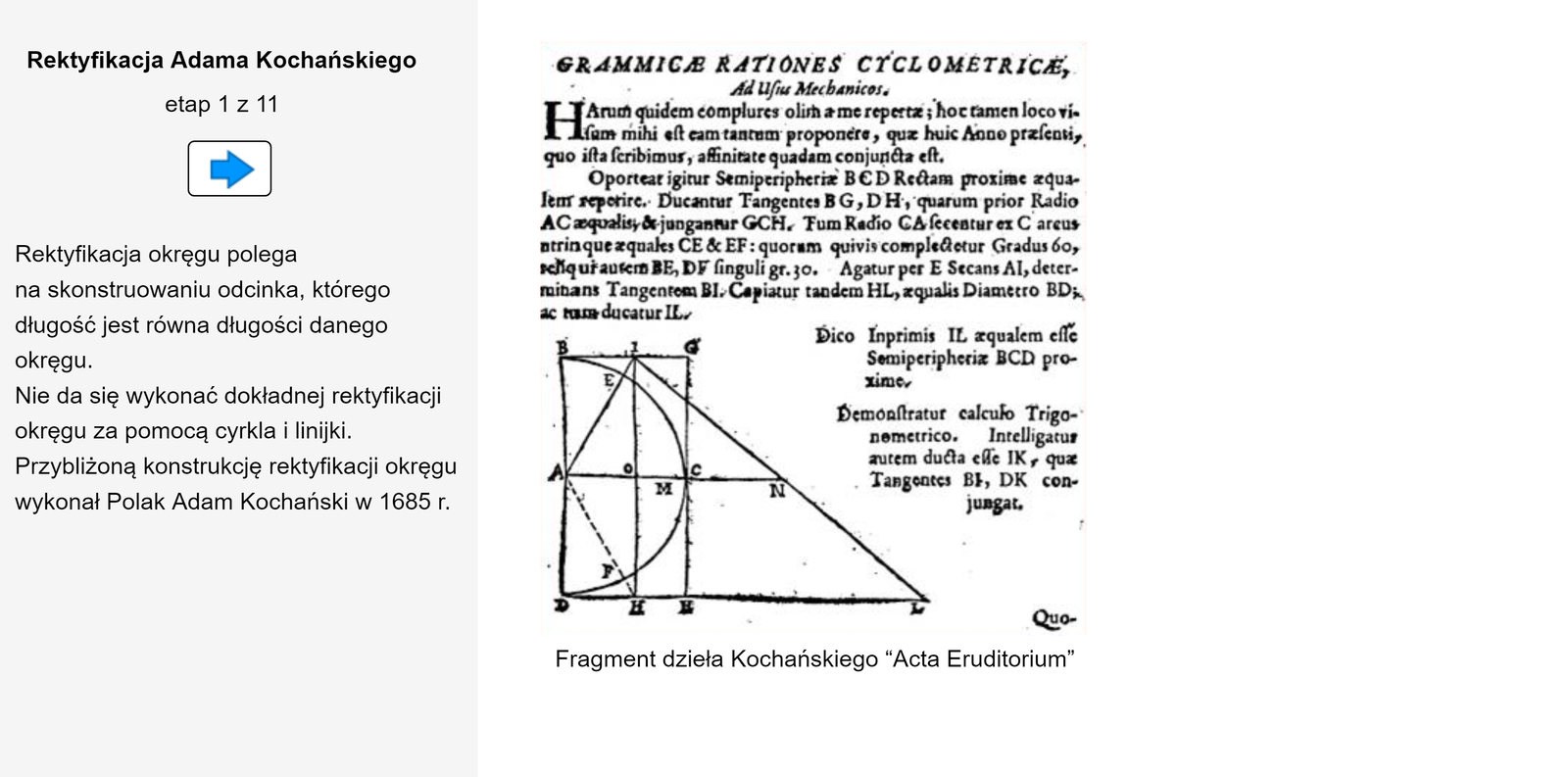
Rektyfikacja lub wyprostowanie okręgu polega na skonstruowaniu odcinka, którego długość jest równa obwodowi danego okręgu.
Jedną z przybliżonych konstrukcji wyprostowania okręgu podał w r. Adam Kochański, nadworny matematyk króla Jana Sobieskiego.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DmQwgAlcy
W w. p.n.e. rzymski architekt Witruwiusz zaproponował sposób pomiaru odległości drogowych, wykorzystujący poruszający się rydwan. Koło takiego rydwanu miało promień . Na pokonanie jednej mili rzymskiej musiało wykonać obrotów.

Oblicz wartość liczby , przyjmowaną przez Witruwiusza.
Rozwiązanie:
W obliczeniach praktycznych najczęściej przyjmuje się, że .
Średnica kółka do deskorolki jest równa . Obliczymy, ile razy obróci się to kółko na drodze długości .
Rozwiązanie:
Obliczamy długość drogi, jaką pokona kółko podczas jednego obrotu, czyli obwód kółka.
Zamieniamy metr na milimetry.
Obliczamy, ile razy obróci się kółko.
Kółko obróci się około razy.
Obliczymy długość okręgu o promieniu .
Rozwiązanie:
Korzystamy ze wzoru na długość okręgu, tym razem nie zastępując liczby jej wartością przybliżoną.
Długość okręgu jest równa .
Obliczymy przybliżoną długość promienia koła o obwodzie .
Rozwiązanie:
Oznaczymy przez przybliżoną długość (w ) promienia koła i skorzystamy ze wzoru ma długość okręgu.
Promień koła ma około długości.
Koniec dużej wskazówki zegara w ciągu godziny pokonał drogę długości . Obliczymy przybliżoną długość tej wskazówki.
Rozwiązanie:
Oznaczmy przez długość (w ) dłuższej wskazówki zegara i skorzystajmy ze wzoru na obwód koła.
Wskazówka ma około długości.
Basia spakowała prezent dla swojej siostry w rulon o średnicy . Czy starczy jej wstążki na obwiązanie tego prezentu w dwóch miejscach skoro na węzeł i kokardę potrzeba ?
Rozwiązanie:
Zaczniemy od obliczenia obwodu rulonu.
Wyznaczymy do tego jego promień, czyli
.
Zatem obwód rulonu jest równy
.
Na jedno obwiązanie potrzeba , zatem na dwa .
Oznacza to, że Basi nie starczy wstążki na obwiązanie prezentu w dwóch miejscach.
Sprawdzimy, czy z drutu o długości można uformować trzy obręcze, każda o promieniu ?
Rozwiązanie:
Najpierw obliczymy obwód jednej obręczy.
.
Zatem na trzy obręcze potrzeba:
.
Oznacza to, że drutu nie wystarczy na wykonanie trzech obręczy o promieniu każda.
Która z figur ma większy obwód: okrąg o promieniu , czy trójkąt równoboczny o boku długości ?
Rozwiązanie:
Zacznijmy od wyznaczenia obwodu okręgu, czyli
.
Obwód trójkąta jest równy .
Wynika stąd, że obwód okręgu jest większy od obwodu trójkąta równobocznego.
Odpowiedź: Promień koła wynosi 1. , 2. , 3. , 4. , 5. .
Odpowiedź: Średnica kosza wynosi około Tu uzupełnij.
- Jeśli dwa okręgi mają równe promienie, to są przystające.
- Jeśli dwa okręgi mają równe obwody, to są współśrodkowe.
- Długość okręgu wyraża się zawsze liczbą wymierną.
- Dla każdego okręgu stosunek jego obwodu do średnicy jest stały.
- jest mniejszy od
- jest równy
- większy od
Odpowiedź: Wstążka powinna mieć długość okołó 1. , 2. , 3. , 4. , 5. , 6. .
Oblicz, ile razy obwód koła o promieniu jest większy od: długości okręgu o średnicy
Odpowiedź: Obwód jest większy Tu uzupełnij razy. długości okręgu o promieniu
Odpowiedź: Obwód jest większy Tu uzupełnij razy.
Odpowiedź: Długość okręgu zwiększy się Tu uzupełnij razy.
Oblicz obwód zacieniowanej figury przedstawionej na rysunku.
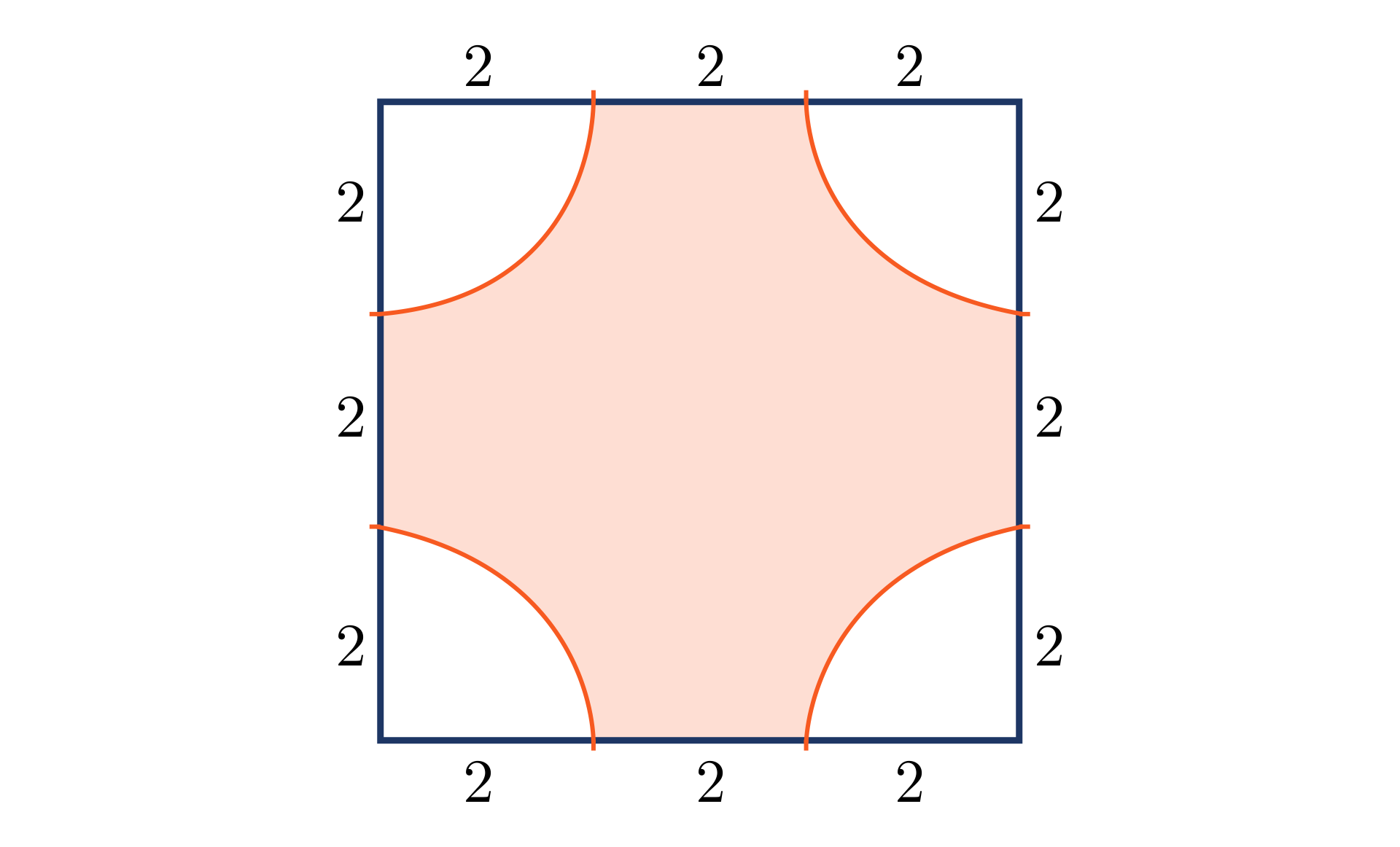
- Suma obwodu kwadratu o boku długości i obwodu połowy okręgu o promieniu długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Różnica obwodu trójkąta równobocznego o boku długości i obwodu czwartej części okręgu o średnicy długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Suma obwodu prostokąta o bokach długości i oraz obwodu trzeciej części okręgu o promieniu długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Różnica obwodu rombu o boku długości i obwodu połowy okręgu o średnicy długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
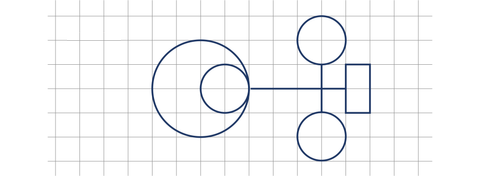
Oblicz łączną długość narysowanych linii. Przyjmij długość jednej kratki jako odcinek jednostkowy.
Tomek zwinął mapę Polski w rulon o średnicy . Ile sznurka potrzebuje na związanie tego rulonu, jeżeli na kokardę potrzebuje dodatkowo sznurka?
Martyna postanowiła ogrodzić swój ogródek w kształcie ćwiartki koła o promieniu . Siatka ogrodzeniowa pakowana jest w rolkach po . Ile paczek musi kupić Martyna, aby ogrodzić swój ogród, uwzględniając miejsce na furtkę szerokości ? Przyjmij .