Dodawanie i odejmowanie wyrażeń algebraicznych
Pole powierzchni prostopadłościanu o krawędziach długości , , obliczamy dodając pola wszystkich ścian tej bryły.
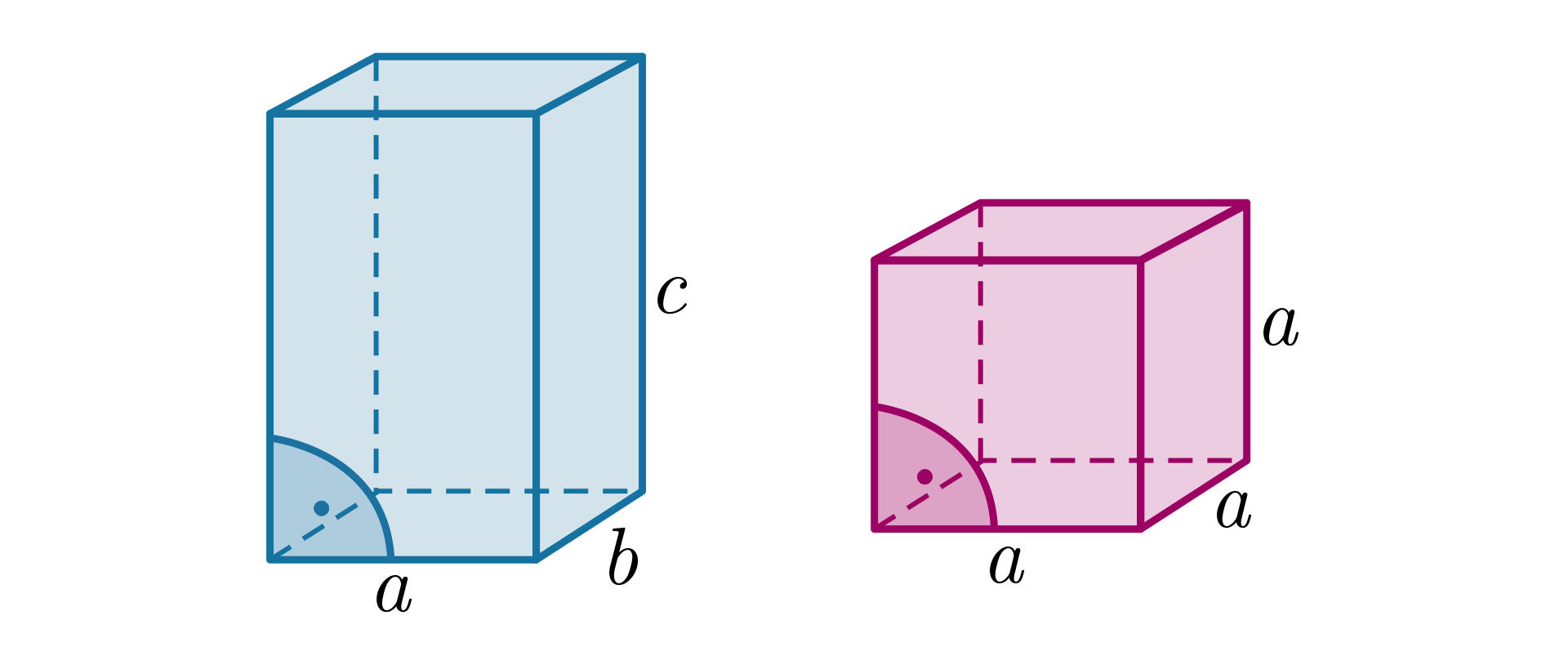
Jeśli wszystkie krawędzie prostopadłościanu są równe , to wzór na pole powierzchni prostopadłościanu można zapisać w postaci sumy algebraicznej:
Chcąc sprowadzić ten wzór do najprostszej postaci, dodajemy wyrazy sumy.
W tym materiale będziemy nie tylko dodawać wyrażenia algebraiczne, ale również będziemy je odejmować.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Gra edukacyjnaGra edukacyjna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Dodasz wyrażenia algebraiczne.
Odejmiesz wyrażenia algebraiczne.
Przekształcisz wyrażenia algebraiczne i zapiszesz je w najprostszej postaci.
Zapiszesz treść i odpowiedź do zadania w postaci wyrażenia algebraicznego.

Po podwórku chodzą gęsi, kaczki i kury. Kur jest o więcej niż kaczek. Gęsi jest o mniej niż kur. Ile wszystkich ptaków chodzi po podwórku?
Z treści zadania nie można wywnioskować, ile kaczek chodzi po podwórku. Oznaczymy więc liczbę kaczek literą .
Wtedy liczba kur jest równa , a liczba gęsi .

Liczbę wszystkich ptaków chodzących po podwórku zapisujemy za pomocą wyrażenia algebraicznego:
Wyrażenie to możemy zapisać w prostszej postaci, wykonując redukcję wyrazów podobnych.
Wyrażenie, które przekształciliśmy, to suma algebraicznasuma algebraiczna.
Sumą algebraiczną nazywamy sumę jednomianów.
Jednomiany, które dodajemy to wyrazy sumy.
Wyrazy podobne występujące w sumie algebraicznej można redukować.
Tabelka przedstawia sumy algebraiczne i wyrazy tych sum.
Suma algebraiczna | Wyrazy sumy |
|---|---|
, , | |
, , , | |
, , |
Odejmowanie można zastąpić dodawaniem liczby przeciwnej, zatem sumą algebraicznąsumą algebraiczną jest też różnica jednomianówjednomianów.
Zapiszemy w najprostszej postaci wyrażenie .
Grupujemy wyrazy podobne i wykonujemy dodawanie.
Zapiszemy za pomocą wyrażenia algebraicznego:
sumę czterech kolejnych liczb naturalnych,
sumę czterech kolejnych liczb naturalnych nieparzystych,
sumę czterech kolejnych liczb naturalnych podzielnych przez trzy.
Rozwiązanie:
Oznaczmy przez najmniejszą z rozważanych liczb naturalnych. Kolejne liczby naturalne różnią się o .
Wtedy:
– pierwsza liczba naturalna,
– druga liczba naturalna,
– trzecia liczba naturalna,
– czwarta liczba naturalna.
Suma liczb:
.sposób:
Oznaczmy przez najmniejszą z rozważanych liczb nieparzystych naturalnych. Kolejne liczby różnią się o .
Zatem:
– pierwsza liczba nieparzysta,
– druga liczba nieparzysta,
– trzecia liczba nieparzysta,
– czwarta liczba nieparzysta.
Suma liczb:
.
sposób:
Kolejne liczby nieparzyste to: , , , , , Są to liczby, które przy dzieleniu przez dają resztę .
Oznaczmy przez dowolną liczbę naturalną dodatnią. Wtedy cztery kolejne liczby nieparzyste można zapisać w postaci:
, , , .
Suma liczb:
.sposób:
Oznaczmy przez pierwszą z rozważanych liczb podzielnych przez . Kolejne liczby podzielne przez różnią się o .
Wtedy:
– pierwsza liczba podzielna przez trzy,
– druga liczba podzielna przez trzy,
– trzecia liczba podzielna przez trzy,
– czwarta liczba podzielna przez trzy.
Suma liczb:
.
sposób:
Kolejne liczby naturalne podzielne przez trzy to: , , , , , Są to kolejne wielokrotności liczby trzy.
Oznaczmy przez dowolną liczbę naturalną.
Wtedy cztery kolejne wielokrotności liczby trzy można zapisać w postaci: , , , .
Suma liczb:
.
Zapiszemy w najprostszej postaci wyrażenie algebraiczne, stanowiące odpowiedź do poniższego zadania.
W sadzie rosną grusze, śliwy, jabłonie i czereśnie. Grusz jest dwa razy więcej niż śliw, jabłoni jest tyle ile grusz i śliw razem. Czereśni rosło początkowo trzy razy tyle ile pozostałych drzew.
Niestety wichura zniszczyła pięć czereśni.
Obliczymy, ile co najmniej wszystkich drzew rośnie teraz w sadzie.
Oznaczymy przez liczbę śliw rosnących w ogrodzie, przez liczbę wszystkich drzew rosnących w ogrodzie. Potrzebne dane zamieścimy w tabelce.
Liczba rosnących teraz w ogrodzie: | |||
|---|---|---|---|
śliw | grusz | jabłoni | czereśni |
Aby obliczyć ile wszystkich drzew rośnie w ogrodzie, dodajemy liczbę rosnących tam śliw, grusz, jabłoni i czereśni.
Redukujemy wyrazy podobne i wykonujemy dodawanie w nawiasie.
Najmniejszą liczbą naturalną dodatnią jest jeden.
Odpowiedź:
W sadzie rośnie co najmniej drzew.
Sumy algebraiczne można dodawać i odejmować. Aby dodać dwie sumy algebraiczne, zapisujemy je w nawiasach, między którymi stawiamy znak plus. Opuszczamy nawiasy i redukujemy wyrazy podobne.
Jeżeli przed nawiasem, w którym zapisana jest suma algebraicznasuma algebraiczna stoi znak plus (lub nie ma żadnego znaku), to opuszczając nawias, znaki w nawiasie pozostawiamy bez zmiany.
Niech i . Zapiszemy w najprostszej postaci wyrażenie
Opuszczamy nawiasy (nie zmieniając znaków!) i redukujemy wyrazy podobne.
Odejmując dwie sumy algebraiczne postępujemy podobnie, jak przy dodawaniu sum algebraicznych. Sumy zapisujemy w nawiasach, między którymi stawiamy znak minus. Opuszczając nawias – zmieniamy znaki na przeciwne w sumie, którą odejmujemy.
Odejmując dwie sumy algebraiczne, w sumie, przed którą stoi znak minus, opuszczając nawias, zmieniamy znaki na przeciwne.
Niech i . Zapiszemy w najprostszej postaci wyrażenie .
Opuszczając nawiasy, zmieniamy znaki w wyrażeniu na przeciwne.
Redukujemy wyrazy podobne.
Krystian wybrał się rowerem z miejscowości Pojutrze do miejscowości Przedwczoraj, oddalonej o . Pierwszego dnia przejechał , drugiego dnia , a pozostałą część drogi przebył trzeciego dnia.
Obliczymy, ile kilometrów przejechał Krystian trzeciego dnia.
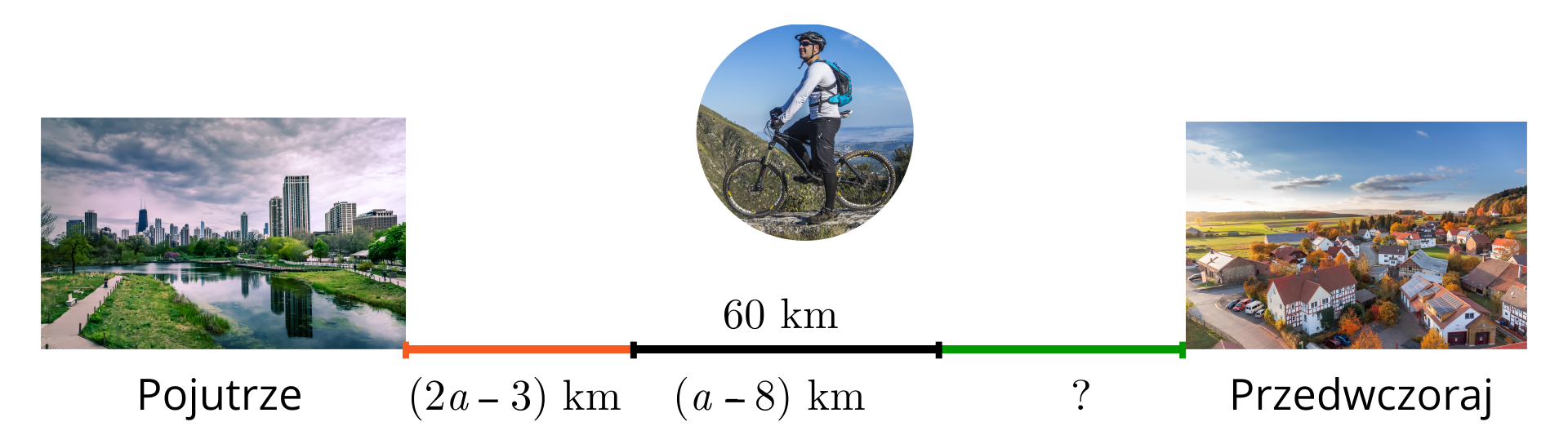
Pierwszego i drugiego dnia Krystian przejechał łącznie .
Zatem do przejechania zostało mu
.
Zapiszemy otrzymane wyrażenie w najprostszej postaci. Najpierw wykonujemy działania w nawiasie kwadratowym.
Przed nawiasem stoi znak minus – opuszczając nawias, zmieniamy znaki w nawiasie na przeciwne.
Odpowiedź:
Krystian trzeciego dnia przejechał .
Notatki
Gra edukacyjna
Sprawdź swoje umiejętności dodawania i odejmowania wyrażeń algebraicznych. Zagraj w grę i postaraj się wydostać z pułapki. Pamiętaj, aby przed zapisaniem wyniku obliczeń zredukować wyrazy podobne.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PDmmuq6Fy
Etap pierwszy:
Etap drugi:
Zapisz wyrażenie w najprostszej postaci.
Zapisz wyrażenie w najprostszej postaci i oblicz wartość wyrażenia dla i .
Tadek ma lat. Mama Tadka jest dwa razy starsza, a tato jest o lata starszy od mamy. Ile lat będą mieli łącznie za dwa lata?
Zestaw ćwiczeń interaktywnych
Czwarta zapisana przez niego czwarta liczba to: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Wskaż każde zdanie prawdziwe. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5.
Połącz każde z wyrażeń z odpowiadającym mu wyrażeniem otrzymanym po wykonaniu wskazanych działań i redukcji wyrazów podobnych. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
Zaznacz, które stwierdzenie jest prawdziwe, a które fałszywe.. Basia ma teraz cukierki.. Możliwe odpowiedzi: Prawda, Fałsz. Adam ma teraz co najmniej sześć cukierków.. Możliwe odpowiedzi: Prawda, Fałsz. Adam ma teraz mniej cukierków niż Basia.. Możliwe odpowiedzi: Prawda, Fałsz. Basia i Adam mają teraz razem cukierków.. Możliwe odpowiedzi: Prawda, Fałsz
Ewa jest o lata młodsza od Jurka i razy starsza od Pawła, który ma lat.
Zapisz wyrażenia, które opisuje ile lat mieli razem Ewa, Jurek i Paweł lata temu.
Zapisz wyrażenie, które opisuje, ile lat będą mieli razem Ewa, Jurek i Paweł za lata.
Dorota kupiła jabłek w cenie za kilogram, gruszek w cenie za kilogram i kilogramy śliwek w cenie za kilogram. Dała kasjerce banknot stuzłotowy. Ile złotych reszty otrzymała?
Słownik
sumą algebraiczną nazywamy sumę jednomianów.
wyrażenie będące iloczynem liczb i liter (może być też sama liczba lub sama litera).
Bibliografia
Gonick L., (2016), Algebra w obrazkach, Warszawa: Prószyński i S‑ka.