Dowody algebraiczne - zpe.gov.pl

RHAF8RvlFAH3V

Często w rozmowach o matematyce, słyszy się, że „jest to nauka ścisła”. Oznacza to, że dla matematyka stwierdzenie, dotyczące na przykład figur geometrycznych lub zależności liczbowych jest dopiero wtedy prawdziwe, gdy zostanie udowodnione. W przeciwnym razie pozostaje hipotezą. Dowód to rozumowanie, przebiegające zgodnie z określonymi regułami. Jeśli jakieś zdanie, opisujące obiekty matematyczne, zostanie udowodnione, to nazywamy je twierdzeniem.

Dowodzenie twierdzeń pozwala na doskonalenie umiejętności dobierania trafnych argumentów, precyzyjnego wyrażania myśli, logicznego myślenia.

W tym materiale poznasz przykłady prostych twierdzeń algebraicznych i sposoby ich dowodzenia.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Prezentacja multimedialnaPrezentacja multimedialna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Podasz przykłady stwierdzeń, które są i które nie są twierdzeniami matematycznymi.
Udowodnisz proste twierdzenie algebraiczne.
Odróżnisz dowód wprost od dowodu nie wprost.

Twierdzenie to zwykle zdanie złożone. Pierwsza część zdania to założenie (najczęściej zaczynające się od sformułowania Jeżeli ...), a druga to teza (zazwyczaj poprzedzona słowem to ...).

RyjONOw9Bqr8n

Na grafice zostało zapisane zdanie: Jeżeli liczba naturalna jest podzielna przez cztery, to jest podzielna przez dwa. Część tego zdania "liczba naturalna jest podzielna przez cztery" jest nazywana założeniem, a część "jest podzielna przez dwa" nazywamy tezą. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Założenie nie zawsze zaczyna się od Jeżeli ... . Na przykład twierdzenie zapisane powyżej można sformułować w postaci:

Liczba naturalna podzielna przez cztery jest podzielna przez dwa.

Matematycy znają wiele sposobów dowodzenia twierdzeń. Jednym z nich jest dowód wprostdowód wprostdowód wprost.
Kolejne kroki dowodu muszą wynikać z poprzednich lub są zdaniami, które w danej teorii przyjmuje się za oczywiste.

Ciekawostka

Najczęściej koniec dowodu oznacza się c.n.d. (co należało dowieść). Współcześnie stosowane są też symbole w postaci kwadratu, prostokąta lub trójkąta.

R1GH7j24mdCrb

Na grafice ukazane są prostokąty o różnych rozmiarach i jeden trójkąt. Trójkąt i część z prostokątów jest wypełniona kolorem czarnym, a pozostałe mają tylko obramowanie w tym kolorze. Kształty rozłożone są w nieregularny sposób. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Sposób dowodzenia metodą wprost, prześledzimy na kilku przykładach.

Przykład 1

Wykażemy, że liczba $A = 2^{100} + 3 \cdot 2^{99} - 2^{98}$ jest podzielna przez $9$ .

Zauważmy najpierw, że twierdzenie, które mamy udowodnić, można zapisać nieco inaczej:
jeżeli liczba $A$ jest równa $2^{100} + 3 \cdot 2^{99} - 2^{98}$ , to liczba ta jest podzielna przez $9$ .

Wtedy wyraźnie widać, która część zdania to założenie, a która to teza.

Założenie	Teza
$A = 2^{100} + 3 \cdot 2^{99} - 2^{98}$	Liczba $A$ jest podzielna przez $9$ .

Pokażemy teraz, jak kolejne kroki dowodu poprowadzą nas od założenia do tezy.

Dowód
Przekształcenia	Opis
$A = 2^{100} + 3 \cdot 2^{99} - 2^{98}$ $A = 2^{98} (2^{100 - 98} + 3 \cdot 2^{99 - 98} - 1)$	Przekształcamy wyrażenie stojące po prawej stronie znaku równości. Wyłączamy wspólny czynnik przed nawias.
$A = 2^{98} (2^{2} + 3 \cdot 2^{1} - 1)$	Korzystamy z własności działań na potęgach.
$A = 2^{98} (4 + 6 - 1)$ $A = 2^{98} \cdot 9$	Wykonujemy działania w nawiasie.
$A = 9 \cdot 2^{98}$	Zapisujemy liczbę $A$ w postaci iloczynu, którego pierwszym czynnikiem jest $9$ .
$A = 9 \cdot 2^{98}$ , gdzie $2^{98}$ jest liczbą naturalną.	Liczbę $A$ przedstawiliśmy w postaci iloczynu liczby $9$ i pewnej liczby naturalnej (czyli $2^{98}$ ), zatem liczba $A$ jest podzielna przez $9$ . Co należało dowieść.

Przykład 2

Wykażemy, że dla każdej liczby $a$ różnej od zera wartość wyrażenia
$W = - 3 (a^{2} - 2) + 4 (a - 1) (a + 1) - a (a + \frac{1}{a})$ jest stała.

Założenie	Teza
Liczba $a$ jest liczbą różną od zera.	Wartość wyrażenia $W$ jest stała.

Dowód, który mamy przeprowadzić jest dość prosty. Przekształcenia, które wykonamy, są podobne do tych, które byśmy wykonywali, mając polecenie: zapisz w prostszej postaci wyrażenie.

Dowód
Przekształcenia	Opis
$W = - 3 (a^{2} - 2) + 4 (a - 1) (a + 1) - a (a + \frac{1}{a}) =$ $= - 3 a^{2} + 6 + 4 (a^{2} + a - a - 1) - a^{2} - \frac{a}{a} =$ $= - 3 a^{2} + 6 + 4 a^{2} - 4 - a^{2} - 1$	Wykonujemy wskazane działania.
$W = (- 3 a^{2} + 4 a^{2} - a^{2}) + (6 - 4 - 1)$	Grupujemy wyrazy podobne.
$W = 0 + 1$	Redukujemy wyrazy podobne.
$W = 1$	Wartość wyrażenia jest równa liczbie $1$ , a więc jest stała dla każdej liczby $a$ różnej od zera, co należało dowieść.

Przykład 3

Wykażemy, że suma trzech kolejnych liczb naturalnych dodatnich jest nie mniejsza od $6$ .

W tym przypadku nie mamy w treści zadania podanych konkretnych liczb. Wiemy natomiast, że mamy do czynienia z kolejnymi liczbami naturalnymi, a więc liczbami z których każda kolejna jest o $1$ większa od poprzedniej. Wystarczy więc jakimś symbolem (np. literą $n$ ) oznaczyć pierwszą z takich liczb i następnie zapisać za jej pomocą kolejne liczby.

Oznaczmy:
$n$ – pierwsza liczba naturalna,
$n + 1$ – druga liczba naturalna,
$n + 2$ – trzecia liczba naturalna.

Założenie	Teza
$n$ – dowolna liczba naturalna dodatnia $n$ , $n + 1$ , $n + 2$ – kolejne liczby naturalne dodatnie	$n + n + 1 + n + 2 ⩾ 6$

Dowód
Przekształcenia	Opis
$L = n + n + 1 + n + 2$	Oznaczmy przez $L$ lewą stronę dowodzonej nierówności.
$L = 3 n + 3$	Wykonujemy wskazane działania.
$3 n ⩾ 3$	Najmniejsza liczba naturalna dodatnia to $1$ , zatem iloczyn liczby $3$ i liczby nie mniejszej od $1$ , będzie nie mniejszy od $3$ .
$L = 3 n + 3 ⩾ 6$	Suma liczby nie mniejszej od $3$ i liczby $3$ jest nie mniejsza od $6$ .
$n + n + 1 + n + 2 ⩾ 6$	Z dowolności liczby $n$ i z powyższego wynika, że suma trzech kolejnych liczb naturalnych dodatnich, jest nie mniejsza od $6$ , co należało dowieść.

Zadania typu wykaż, że mogą dotyczyć nie tylko zależności liczbowych, ale również innej tematyki, na przykład związanej z rachunkiem prawdopodobieństwa.

Przykład 4

W pudełku są tylko kule złote, srebrne i brązowe. Kul srebrnych jest $3$ razy więcej niż złotych. Kul brązowych jest dwa razy mniej niż kul srebrnych i złotych razem. Wykażemy, że prawdopodobieństwo wylosowania z pudełka kuli w kolorze innym niż złoty, jest większe niż $\frac{2}{3}$ .
Teraz rozwiązanie zadania zapiszemy w sposób mniej formalny, niż w poprzednich przykładach.

Oznaczmy:

$x$ – liczba kul złotych, $x$ – liczba naturalna
$3 x$ – liczba kul srebrnych
$\frac{x + 3 x}{2}$ – liczba kul brązowych

Z treści zadania wynika, że liczba wszystkich kul znajdujących się w pudełku jest równa:
$x + 3 x + \frac{x + 3 x}{2}$ .
Przekształcamy otrzymanie wyrażenie.

x + 3 x + \frac{x + 3 x}{2} = 4 x + \frac{4 x}{2} = 4 x + 2 x = 6 x

W pudełku jest więc $6 x$ kul.
Kul w kolorze innym niż złoty, czyli srebrnych i brązowych, jest razem:

3 x + 2 x = 5 x

Zatem prawdopodobieństwo wylosowania kuli w kolorze innym niż złoty, jest równe:

p = \frac{5 x}{6 x} = \frac{5}{6}

Ponieważ
$\frac{2}{3} = \frac{4}{6}$ , to
$\frac{5}{6} > \frac{4}{6}$ , czyli $\frac{5}{6} > \frac{2}{3}$ , co należało wykazać.

Przykład 5

W maju i czerwcu cena gruszek była stała. W lipcu cenę tę obniżono o $20 %$ , a w sierpniu podwyższono o $25 %$ . Wykaż, że sierpniowa cena gruszek jest równa czerwcowej.

Nie znamy konkretnej wartości czerwcowej ceny gruszek, zatem postępujemy tak, jak w poprzednich przykładach, czyli wprowadzamy oznaczenia literowe.

Oznaczmy:
$c$ – czerwcowa cena gruszek (w $zł$ ).

W lipcu cenę obniżono o $20 %$ , zatem stanowi ona $80 %$ ceny początkowej, czyli $0, 8 c zł$ .
W sierpniu tę nową cenę podwyższono o $25 %$ , czyli stanowi ona $125 %$ ceny lipcowej. Jest więc równa $1, 25 \cdot (0, 8 c) zł$ .
Zapisujemy w prostszej postaci uzyskane wyrażenie.

1, 25 \cdot (0, 8 c) = 1, 25 \cdot 0, 8 c = 1 \cdot c = c

Ponieważ $c zł$ jest czerwcową ceną gruszek, zatem cena sierpniowa jest równa cenie czerwcowej, co należało dowieść.

Pokażemy teraz zastosowanie innej metody dowodzenia twierdzeń, zwanej dowodem nie wprostdowód nie wprostdowodem nie wprost. Dowód, z zastosowaniem tej metody, rozpoczynamy od przypuszczenia, że dowodzone twierdzenie jest fałszywe i wykazaniu, że przypuszczenie takie prowadzi do sprzeczności.
Inaczej mówiąc, wykazujemy sprzeczność między zaprzeczeniem dowodzonej tezy, a przyjętymi założeniami.

Ciekawostka

R1WGVGhJZVEAV1

Obraz przedstawia dwóch mężczyzn ubranych w szaty. Jeden tłumaczy coś drugiemu, a ten słucha go z zaciekawieniem. — Źródło: dostępny w internecie: wikipedia.org, licencja: CC BY 3.0.

Dowód nie wprostdowód nie wprostDowód nie wprost, zwany inaczej dowodem przez sprowadzenie do sprzeczności, wprowadził w $V$ w p.n.e. Hipokrates z Chios. Spopularyzował ten sposób dowodzenia Sokrates. Zatem czasem używa się też nazwy dowód sokratejski.

Przykład 6

Wykażemy, że jeżeli kwadrat liczby naturalnej dodatniej $n$ jest podzielny przez $7$ , to liczba $n$ też jest podzielna przez $7$ .

Załóżmy, że liczba $n^{2}$ jest podzielna przez $7$ , ale nieprawda, że liczba $n$ jest podzielna przez $7$ (założenie dowodu nie wprost).
Zauważmy, że jeśli liczba $n^{2}$ jest podzielna przez $7$ , to również iloczyn $n \cdot n$ jest podzielny przez $7$ .
Liczba $7$ jest liczbą pierwszą, zatem jeśli $7$ dzieli iloczyn dwóch liczb, to dzieli przynajmniej jedną z tych liczb. Zatem $7$ jest dzielnikiem liczby $n$ , a więc liczba $n$ dzieli się przez $7$ .
Z założenia o nieprawdziwości tezy (liczba $n$ nie jest podzielna przez $7$ ) doszliśmy do sprzeczności. To pozwala nam przyjąć, że zaprzeczenie tezy jest nieprawdziwe, a prawdziwa jest wyjściowa teza.

Na koniec zauważmy jeszcze, że jeśli chcemy wykazać, że jakaś hipoteza jest nieprawdziwa (czyli nie jest twierdzeniem matematycznym), wystarczy podać przynajmniej jeden przykład, który nie spełnia hipotezy. Jest to tak zwany kontrprzykład.

Przykład 7

Pokażemy, że hipoteza: „Istnieje tylko jedna liczba, której kwadrat jest równy $4$ .” jest nieprawdziwa.
Kontrprzykład: $2^{2} = 4$ i ${(- 2)}^{2} = 4$ . Istnieją więc co najmniej dwie liczby, których kwadrat jest równy $4$ .
Hipoteza jest więc fałszywa, co należało udowodnić.

Notatnik

RSe7EPrRDwRlx

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Prezentacja multimedialna

Polecenie 1

Obejrzyj prezentację, w której znajdziesz przykłady dowodzenia twierdzeń. Staraj się najpierw samodzielnie rozwiązać podane zadanie, a dopiero następnie porównaj z rozwiązaniem zamieszczonym w prezentacji.

RZIS9MZHpXEfY

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1EcVQoyEeLfM

R3TzzadIcdLeB

Ilustracja nawiązująca do treści materiału — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R12YBBdE0zjjC

RZj0UrM3HmKuw

Transkrypcjaazurewhite

Dowód nie polega na podaniu konkretnych obiektów matematycznych (na przykład liczb czy figur geometrycznych), które spełniają dane twierdzenie. Jest to rozumowanie, które przebiega według określonych zasad. Natomiast, aby pokazać, że dana hipoteza nie jest twierdzeniem, wystarczy podać przynajmniej jeden przykład, który nie spełnia tej hipotezy. Dla przykładu wykażemy, że nieprawdziwa jest hipoteza: jeśli liczby $a$ i $b$ są dowolnymi liczbami naturalnymi dodatnimi, to kwadrat sumy tych liczb jest równy sumie kwadratów tych liczb.

R1COpI8znRHGU

RqVW1rx90BWWC

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

W myśl założenia, liczby $a$ i $b$ muszą być liczbami naturalnymi dodatnimi. Przyjmijmy więc, że liczba $a$ jest na przykład równa trzy, a liczba $b$ pięć. Podstawiamy te liczby kolejno do prawej i lewej strony rozpatrywanej równości.

Rbu5ci41l5C84

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przykład drugi
Kwiatki na rysunku budowane są według pewnej reguły. Udowodnimy, że nie istnieje kwiatek składający się z $100$ żółtych płatków, budowany według tej reguły.
Aby rozwiązać to zadanie możemy rysować kolejne figury i ustalać za każdym razem, ile płatków ma dany kwiatek. W ten sposób sprawdzimy, czy kwiatek o stu płatkach istnieje, czy nie. Jednak ten sposób postępowania może być uciążliwy i łatwo prowadzący do błędu. Zatem najpierw spróbujemy odkryć regułę budowania kolejnych kwiatków i opisać ją wzorem.

R173wRFTaPnCm

R1Na0BwEHiDcj

Transkrypcjaazurewhite

R2UvDdYdRkpJC

R1GYxgGWT5oMP

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1FHcIeKFcZCj

R1RwxB3mwyaK0

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1YyoPf6ML4cb

R1JZSbp4r8nMz

Na slajdzie białe tło i kolorowa ramka. W prawym górnym rogu znajduje się napis na czarnym tle. Przykład 3. Niżej zapisany jest tekst. Twierdzenie: jeżeli liczba naturalna jest podzielna przez 16, to jest podzielna przez 4. Pierwsza część zdania jest zaznaczona kolorem różowym, druga zielonym. Poniżej znajduje się kolejna notatka. Twierdzenie odwrotne: jeżeli liczba naturalna jest podzielna przez 4, to jest podzielna przez 16. Pierwsza część zdania jest zaznaczona kolorem różowym, druga zielonym. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

ReHw4P9caqW2G

R7vUf5niwEjKx

Transkrypcjaazurewhite

Wykażemy prawdziwość podanego twierdzenia.
Niech $n$ będzie dowolną liczbą naturalną podzielną przez szesnaście. Liczbę $n$ można zapisać za pomocą iloczynu liczby szesnaście i pewnej liczby naturalnej $t$ . Liczba szesnaście to kwadrat liczby cztery.
Liczbę szesnaście $t$ można zapisać więc za pomocą iloczynu liczby cztery i liczby naturalnej cztery $t$ .
Co oznacza, że liczba $n$ jest podzielna przez cztery, co kończy dowód.

R1Ahd0Pn1rKKB

R1Zc7bqFTosej

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Slajd pierwszy

Mianem twierdzenia matematycznego określa się zwykle hipotezę, która została udowodniona.

Twierdzenie raz udowodnione, pozostaje prawdziwe w każdym czasie.

Dlatego nadal korzystamy z twierdzeń podanych przez takich uczonych jak Pitagoras czy Tales.

Grafiki na planszy przedstawiają greckich uczonych. Pierwsza z nich jest obrazem ukazującym Pitagorasa wraz z uczniami. Zapisuje on swoje dowody w księdze. Druga grafika przedstawia popiersie Talesa. Jest to mężczyzna o krótko ściętych włosach i gęstej brodzie w średnim wieku.

Slajd drugi

Dowód nie polega na podaniu konkretnych obiektów matematycznych (na przykład liczb czy figur geometrycznych), które spełniają dane twierdzenie.

Jest to rozumowanie, które przebiega według określonych zasad.

Natomiast, aby pokazać, że dana hipoteza nie jest twierdzeniem, wystarczy podać przynajmniej jeden przykład, który nie spełnia tej hipotezy.

Dla przykładu wykażemy, że nieprawdziwa jest hipoteza:

jeżeli liczby a i b są dowolnymi liczbami naturalnymi dodatnimi, to kwadrat sumy tych liczb jest równy sumie kwadratów tych liczb.

Slajd trzeci

O to przeprowadzone rozumowanie. Zapisujemy rozważaną równość ${(a + b)}^{2} = a^{2} + b^{2}$ . W myśl założenia, liczby a i b muszą być liczbami naturalnymi dodatnimi. Przyjmijmy więc, że liczba a jest na przykład równa trzy, a liczba b pięć. Podstawiamy te liczby kolejno do prawej i lewej strony rozpatrywanej równości. Wówczas $L = {(a + b)}^{2}$ , czyli $L = {(3 + 5)}^{2} = 8^{2} = 64$ . Następnie $P = a^{2} + b^{2}$ , czyli $P = 3^{2} + 5^{2} = 9 + 25 = 34$ . Porównujemy obie strony dowodzonej równości i otrzymujemy, że $L \neq P$ . Prawa strona nie jest równa lewej, czyli równość nie jest prawdziwa. Zatem postawiona hipoteza jest nieprawdziwa, co należało dowieść.

Slajd czwarty

Przykład drugi

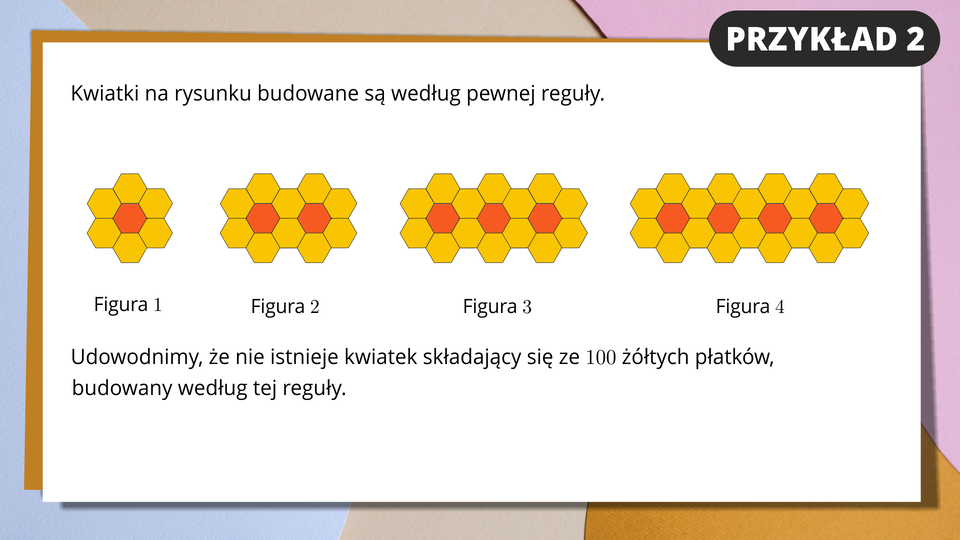
Kwiatki na rysunku budowane są według pewnej reguły.

Udowodnimy, że nie istnieje kwiatek składający się ze stu żółtych płatków, budowany według tej reguły.

Aby rozwiązać to zadanie możemy rysować kolejne figury i ustalać za każdym razem, ile płatków ma dany kwiatek. W ten sposób sprawdzimy, czy kwiatek o stu płatkach istnieje, czy nie.

Jednak ten sposób postępowania może być uciążliwy i łatwo prowadzący do błędu.

Zatem najpierw spróbujemy odkryć regułę budowania kolejnych kwiatków i opisać ją wzorem.

Na planszy slajdu pojawiają się figury w kształcie kwiatków. Każda część kwiatka, czyli środek lub płatek jest w kształcie sześciokąta. Pierwsza figura składa się z środka i sześciu płatków. Druga figura składa się z dwóch środków, ale dwa płatki pomiędzy dwoma środkami są wspólne dla obu kwiatków. Trzecia figura powstaje przez dołożenie trzeciego środka, gdzie również dwa płatki pomiędzy drugim a trzecim środkiem są wspólne. Każda kolejna figura powstaje w ten sam sposób.

Slajd piąty

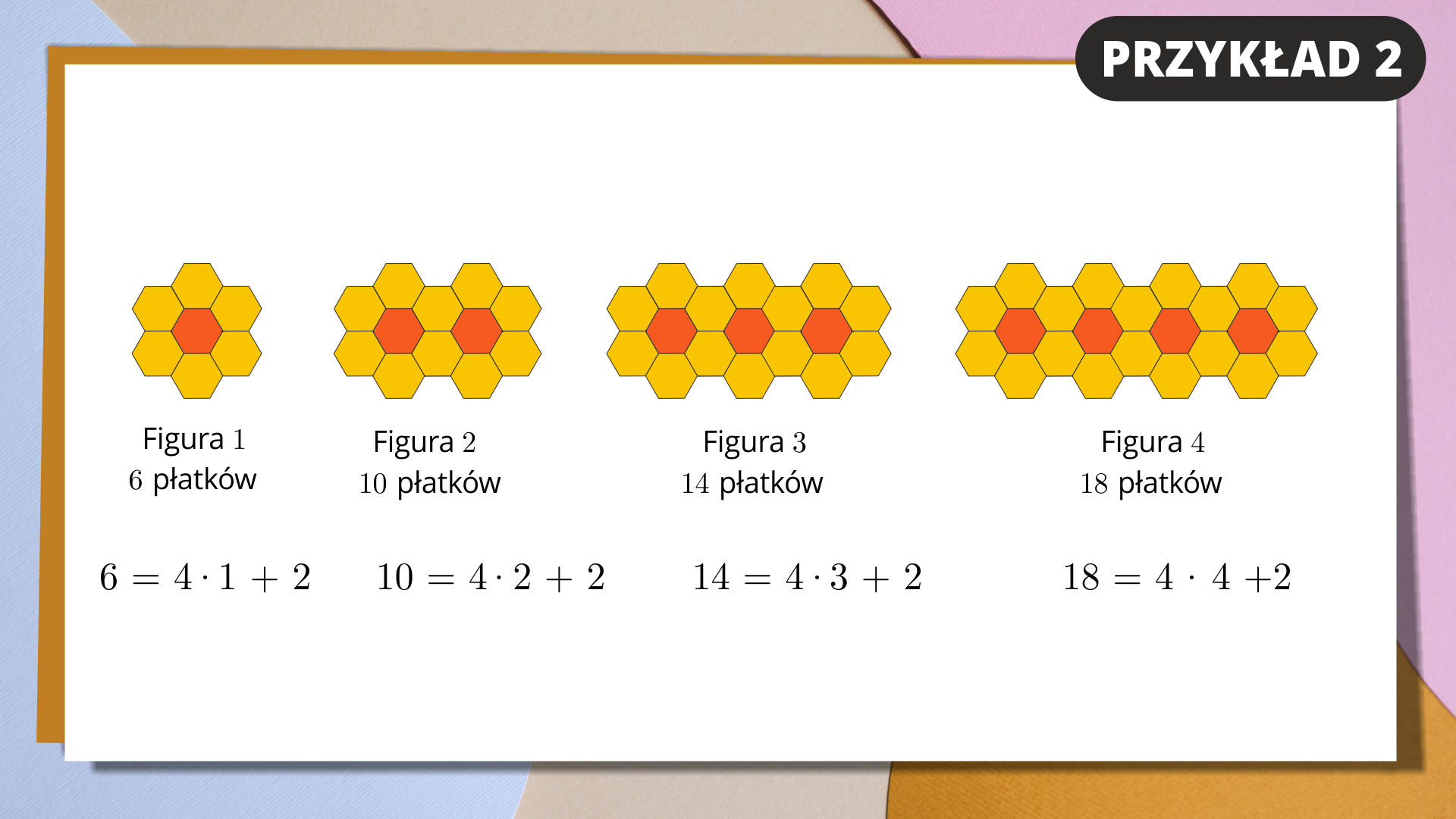
Zauważmy, że pierwsza figura składa się z sześciu płatków, druga z dziesięciu płatków, trzecia z czternastu płatków, czwarta z osiemnastu płatków.

Każdą z tych liczb można zapisać za pomocą sumy liczby dwa i iloczynu liczby cztery przez pewną liczbę naturalną.
Na planszy znajdują się wcześniej opisane kwiatki. Pod pierwszą figurą zapisano $6 = 4 \cdot 1 + 2$ , pod drugą zapisano $10 = 4 \cdot 2 + 2$ , pod trzecią $14 = 4 \cdot 3 + 2$ , a pod czwartą $18 = 4 \cdot 4 + 2$ .

Slajd szósty

Zauważmy, że w iloczynie, którego pierwszym czynnikiem jest liczba cztery, drugi czynnik to liczba opisująca numer figury. Możemy więc zapisać wzór na liczbę płatków figury o numerze $n$ . Zatem $F_{1} = 4 \cdot 1 + 2$ , $F_{2} = 4 \cdot 2 + 2$ , $F_{3} = 4 \cdot 3 + 2$ , $F_{4} = 4 \cdot 4 + 2$ . Otrzymujemy wzór $F_{n} = 4 \cdot n + 2$ .

Slajd siódmy

Chcemy teraz znaleźć numer figury składającej się ze stu płatków.

W tym celu rozwiązujemy odpowiednie równanie. $4 \cdot n + 2 = 100$ , $4 \cdot n = 100 - 2$ , $4 \cdot n = 98$ , $n = \frac{98}{4}$ , $n = 24, 5$ .

Otrzymana liczba nie spełnia warunków zadania, ponieważ nie jest liczbą naturalną. Zatem nie istnieje figura, tworzona według odkrytej przez nas reguły, składająca się ze stu płatków, co należało dowieść.

Slajd ósmy

Przykład trzeci

Twierdzeniem odwrotnym do danego twierdzenia jest zdanie, w którym zamieniono założenie z tezą.

Twierdzenie odwrotne do twierdzenia prawdziwego może być prawdziwe lub fałszywe.

Twierdzenie. Jeżeli liczba naturalna jest podzielna przez szesnaście to jest podzielna przez cztery.

Twierdzenie odwrotne. Jeżeli liczba naturalna jest podzielna przez cztery to jest podzielna przez szesnaście.

Slajd dziewiąty

Wykażemy prawdziwość podanego twierdzenia.
Niech $n$ będzie dowolną liczbą naturalną podzielną przez szesnaście. Liczbę $n$ można zapisać za pomocą iloczynu liczby szesnaście i pewnej liczby naturalnej $t$ . Liczba szesnaście to kwadrat liczby cztery.
Liczbę szesnaście $t$ można zapisać więc za pomocą iloczynu liczby cztery i liczby naturalnej cztery $t$ , czyli $n = 4^{2} \cdot t = 4 \cdot 4 t = 4 (4 t)$ . Co oznacza, że liczba $n$ jest podzielna przez cztery, co kończy dowód.

Slajd dziesiąty

Wykażemy, że twierdzenie odwrotne jest fałszywe.

Fałszywość twierdzenia stwierdzimy przez podanie kontrprzykładu.

Kontrprzykładem wskazującym fałszywość twierdzenia, może być liczba dwadzieścia. Jest to liczba podzielna przez cztery, ale niepodzielna przez szesnaście.

Koniec prezentacji.

Polecenie 2

Uzasadnij fałszywość podanych zdań, wskazując odpowiednie kontrprzykłady.

Suma liczby naturalnej i liczby o $2$ od niej mniejszej jest zawsze liczbą dodatnią.
Suma dwóch kolejnych liczb naturalnych jest zawsze liczbą co najmniej równą $3$ .
Iloczyn liczby naturalnej parzystej i liczby naturalnej nieparzystej jest liczbą nieparzystą.

RNM0YV8suLr75

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Kontrprzykład: $0 + (- 2) = - 2 < 0$ .
Kontrprzykład: $0 + 1 = 1 < 3$ .
Kontrprzykład: $4 \cdot 7 = 28$ – liczba parzysta.

Polecenie 3

Do każdego z podanych twierdzeń sformułuj twierdzenie odwrotne i ustal, czy jest ono prawdziwe, czy fałszywe.

Jeżeli pole kwadratu jest równe $a^{2}$ , to długość boku tego kwadratu jest równa $a$ .
Jeżeli liczba $5$ jest rozwiązaniem równania $x + 7 = 12$ , to jest też rozwiązaniem równania $2 x + 14 = 24$ .
Jeżeli figura jest kwadratem, to ma cztery boki.

R1KjlV8FDa1th

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeżeli długość boku kwadratu jest równa $a$ , to pole tego kwadratu jest równe $a^{2}$ . PRAWDA
Jeżeli liczba $5$ jest rozwiązaniem równania $2 x + 14 = 24$ , to jest też rozwiązaniem równania $x + 7 = 12$ . PRAWDA
Jeżeli figura ma cztery boki, to jest kwadratem. FAŁSZ

Polecenie 4

Wykaż, że suma dwóch kolejnych liczb naturalnych jest liczbą nieparzystą.

RcJn19DyU7dAi

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Podsumowanie
Matematyka posługuje się własnym językiem, opisującym różne jej obiekty. Zdaniami tego języka są w szczególności twierdzenia. Żeby pewne zdania zostało uznane za twierdzenie musi posiadać ścisłe uzasadnienie, czyli dowód. W matematyce istniej wiele sposobów dowodzenia twierdzeń. W tym materiale poznaliśmy dwa rodzaje dowodów – dowód wprostdowód wprostdowód wprost i dowód nie wprostdowód nie wprostdowód nie wprost.

Zestaw ćwiczeń interaktywnych

Ćwiczenie 1

Rxy2hAvFNxVER

Łączenie par. Zaznacz, które stwierdzenie jest prawdziwe, a które fałszywe.. Wystarczy podać jeden przykład nie spełniający danej hipotezy (czyli kontrprzykład), aby wykazać fałszywość tej hipotezy.. Możliwe odpowiedzi: Prawda, Fałsz. Wystarczy podać przynajmniej

100

przykładów spełniających daną hipotezę, aby wykazać prawdziwość tej hipotezy.. Możliwe odpowiedzi: Prawda, Fałsz. Aby wykazać prawdziwość jakiejś hipotezy, należy rozpatrzeć wszystkie możliwe przypadki.. Możliwe odpowiedzi: Prawda, Fałsz. Twierdzenie odwrotne do danego twierdzenia jest zawsze prawdziwe.. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 2

RcYbA43f80eBB

Połącz w pary dwie części zdania tak, aby otrzymać twierdzenie prawdziwe. Suma trzech kolejnych liczb naturalnych dodatnich Możliwe odpowiedzi: 1. jest liczbą podzielną przez

3

., 2. jest liczbą podzielną przez

8

., 3. jest liczbą podzielną przez

31

., 4. jest liczbą podzielną przez

7

. Suma trzech kolejnych naturalnych dodatnich potęg liczby

2

Możliwe odpowiedzi: 1. jest liczbą podzielną przez

3

., 2. jest liczbą podzielną przez

8

., 3. jest liczbą podzielną przez

31

., 4. jest liczbą podzielną przez

7

. Suma trzech kolejnych naturalnych dodatnich potęg liczby

5

Możliwe odpowiedzi: 1. jest liczbą podzielną przez

3

., 2. jest liczbą podzielną przez

8

., 3. jest liczbą podzielną przez

31

., 4. jest liczbą podzielną przez

7

. Suma czterech kolejnych liczb naturalnych nieparzystych Możliwe odpowiedzi: 1. jest liczbą podzielną przez

3

., 2. jest liczbą podzielną przez

8

., 3. jest liczbą podzielną przez

31

., 4. jest liczbą podzielną przez

7

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R9L2xyVMH1ZMk

Ćwiczenie 3

Nazwij każde z poniższych stwierdzeń, przeciągając odpowiedni wyraz.
TWIERDZENIE - jeśli stwierdzenie jest prawdziwe,
HIPOTEZA - jeśli stwierdzenie jest nieprawdziwe.
Liczba

a

jest dodatnią liczbą naturalną parzystą.

Średnia arytmetyczna liczby $a$ i liczby o $2$ od niej większej jest liczbą nieparzystą. 1. TWIERDZENIE, 2. TWIERDZENIE, 3. TWIERDZENIE, 4. HIPOTEZA
Iloczyn liczby $a$ i liczby o połowę od niej mniejszej jest liczbą naturalną. 1. TWIERDZENIE, 2. TWIERDZENIE, 3. TWIERDZENIE, 4. HIPOTEZA
Różnica liczby $a$ i liczby o $1$ od niej mniejszej może być liczbą ujemną. 1. TWIERDZENIE, 2. TWIERDZENIE, 3. TWIERDZENIE, 4. HIPOTEZA
Suma liczby $a$ i liczby o $4$ od niej większej jest liczbą parzystą. 1. TWIERDZENIE, 2. TWIERDZENIE, 3. TWIERDZENIE, 4. HIPOTEZA

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rc7o9Xd1eUtpv

Ćwiczenie 4

Poukładaj w odpowiedniej kolejności dowód poniższego twierdzenie.
Twierdzenie:
Trzecia część połowy liczby naturalnej dodatniej jest mniejsza od

20 %

tej liczby. Elementy do uszeregowania: 1. Oznaczmy:

R = 0, 2 a - \frac{1}{6} a

., 2.

20 %

liczby

a

0, 2 a

., 3. Sprowadzamy do wspólnego mianownika i wykonujemy odejmowanie., 4. Oznaczymy:

a

- dowolna liczba naturalna dodatnia., 5. Zapiszemy w prostszej postaci różnicę

R

R = 0, 2 a - \frac{1}{6} a = \frac{2}{10} a - \frac{1}{6} a = \frac{1}{5} a - \frac{1}{6} a

, 6. Połowa liczby

a

\frac{1}{2} a

., 7. Trzecia część połowy liczby

a

\frac{1}{3} \cdot \frac{1}{2} a

, czyli

\frac{1}{6} a

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 5

RqMNtkTAJJIy9

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

Rg07laeLO7zho

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Liczba $\frac{a}{b}$ to odwrotność liczby $\frac{b}{a}$ .

Ćwiczenie 7

Wykaż, że jeżeli $a$ , $b$ są takimi liczbami, że $a + b = 4$ i $a - b = 2$ , to liczba $a$ jest nieparzysta.

R1UDNQ7HhUBIA

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wyznacz z pierwszego równania liczbę $b$ i podstaw do drugiego równania.

Z równania $a + b = 4$ wyznaczamy liczbę $b$ .

b = 4 - a

Wyznaczoną liczbę podstawiamy do drugiego równania i wyznaczamy liczbę $a$ .

a - b = 2

a - (4 - a) = 2

a - 4 + a = 2

2 a = 6

$a = 3$ – liczba nieparzysta, co należało udowodnić.

Ćwiczenie 8

Udowodnij, że suma liczby dwucyfrowej i liczby utworzonej z tych samych cyfr, zapisanych w odwrotnej kolejności, jest podzielna przez $11$ .

RgnyMevWJXNsu

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Liczbę, której cyfrą dziesiątek jest $x$ , a cyfrą jedności jest $y$ , można zapisać w postaci: $10 x + y$ .
Wtedy liczba o przestawionych cyfrach to: $10 y + x$ .

$x$ – cyfra jedności danej liczby i $x \neq 0$ (czyli $x$ to $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ )
$y$ – cyfra dziesiątek danej liczby i $y \neq 0$ (czyli $y$ to $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ )
$10 x + y$ – dana liczba
$10 y + x$ – liczba utworzona z tych samych cyfr, zapisanych w odwrotnej kolejności
$(10 x + y) + (10 y + x)$ – suma liczb
Przekształcamy zapisaną sumę.
$(10 x + y) + (10 y + x) = 10 x + y + 10 y + x = 11 x + 11 y = 11 (x + y)$
$11 (x + y)$ – iloczyn liczby $11$ i liczby naturalnej, zatem liczba podzielna przez $11$ , co należało udowodnić.

Słownik

dowód wprost

dowód, w którym rozpoczyna się od założeń, przeprowadza się wnioskowanie i dochodzi się do tezy twierdzenia.

dowód nie wprost

dowód, który polega na zaprzeczeniu tezy dowodzonego twierdzenia i wykazaniu, że przyjęcie takiego zaprzeczenia prowadzi do sprzeczności.

Bibliografia

Zarzycki P., (2007), Wszystkie twierdzenia duże i małe, Opole: Wydawnictwo NOWIK.