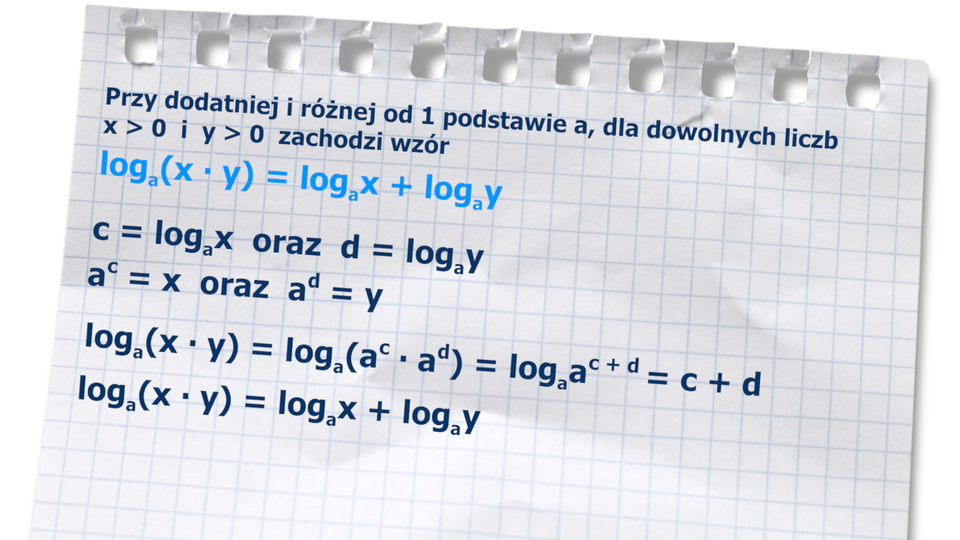Działania na logarytmach. Przykłady

W tym materiale zawarte są wiadomości dotyczące praw działań na logarytmach. Poznasz podstawowe twierdzenia dotyczące tych działań oraz przykłady, które pokazują w jaki sposób je stosować.

Logarytm iloczynu

Przykład 1

Wykażemy, że

\log_{8} 2 + \log_{8} 32 = 2

Oznaczmy $c = \log_{8} 2$ oraz $d = \log_{8} 32$ . Korzystając z definicji logarytmu, otrzymujemy $8^{c} = 2$ oraz $8^{d} = 32$ . Zatem

\log_{8} (8^{c} \cdot 8^{d}) = \log_{8} (2 \cdot 32) = \log_{8} 64 = \log_{8} 8^{2} = 2

Równocześnie

\log_{8} (8^{c} \cdot 8^{d}) = \log_{8} 8^{c + d} = c + d

Zachodzi więc równość

c + d = 2

czyli stosując przyjęte oznaczenia

\log_{8} 2 + \log_{8} 32 = 2

W ten sposób dowód został zakończony.

Logarytm iloczynu

Twierdzenie: Logarytm iloczynu

Jeżeli liczba $a$ jest dodatnia i różna od $1$ , to dla dowolnych liczb dodatnich $x$ i $y$

\log_{a} (x \cdot y) = \log_{a} x + \log_{a} y

Dowód

Oznaczmy $c = \log_{a} x$ oraz $d = \log_{a} y$ . Korzystając z definicji logarytmu, otrzymujemy $a^{c} = x$ oraz $a^{d} = y$ . Zatem

\log_{a} (x \cdot y) = \log_{a} (a^{c} \cdot a^{d}) = \log_{a} a^{c + d} = c + d

Stosując przyjęte oznaczenia, mamy

\log_{a} (x \cdot y) = \log_{a} x + \log_{a} y

To kończy dowód.

RXJrV9vofB9Bh1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 2

Wykażemy, że

$\log_{9} 3 + \log_{9} 243 = 3$ .
$\log_{125} \frac{1}{5} + \log_{125} 625 = 1$ .
$\log_{12} 9 + \log_{12} 16 = 2$ .
$\log 2 + \log 25 + \log 0, 002 = - 1$ .

Rozwiązanie:

Korzystamy z twierdzenia o logarytmie iloczynu.

$\log_{9} 3 + \log_{9} 243 = \log_{9} (3 \cdot 243) = \log_{9} 729 = \log_{9} 9^{3} = 3$ .
$\log_{125} \frac{1}{5} + \log_{125} 625 = \log_{125} (\frac{1}{5} \cdot 625) = \log_{125} 125 = 1$ .
$\log_{12} 9 + \log_{12} 16 = \log_{12} (9 \cdot 16) = \log_{12} 144 = \log_{12} 12^{2} = 2$ .
Ponieważ $\log 2 + \log 25 = \log (2 \cdot 25) = \log 50$ , więc $\log 2 + \log 25 + \log 0, 002 = \log 50 + \log \frac{1}{500} = \log (50 \cdot \frac{1}{500}) = \log \frac{1}{10} =$
$= \log 10^{- 1} = - 1$ .

Logarytm ilorazu

Przykład 3

Wykażemy, że $\log_{3} 135 - \log_{3} 5 = 3$ .

Oznaczmy $c = \log_{3} 135$ oraz $d = \log_{3} 5$ . Korzystając z definicji logarytmu, otrzymujemy

3^{c} = 135

3^{d} = 5

Zatem

\log_{3} (3^{c} : 3^{d}) = \log_{3} (135 : 5) = \log_{3} 27 = \log_{3} 3^{3} = 3

Równocześnie

\log_{3} (3^{c} : 3^{d}) = \log_{3} 3^{c - d} = c - d

Zachodzi więc równość

c - d = 3

czyli stosując przyjęte oznaczenia

\log_{3} 135 - \log_{3} 5 = 3

W ten sposób dowód został zakończony.

Logarytm ilorazu

Twierdzenie: Logarytm ilorazu

Przy dodatniej i różnej od $1$ podstawie $a$ dla dowolnych liczb $x > 0$ i $y > 0$ prawdziwa jest równość

\log_{a} \frac{x}{y} = \log_{a} x - \log_{a} y

Dowód

Oznaczmy $c = \log_{a} x$ oraz $d = \log_{a} y$ . Korzystając z definicji logarytmu, otrzymujemy $a^{c} = x$ oraz $a^{d} = y$ . Zatem

\log_{a} \frac{x}{y} = \log_{a} \frac{a^{c}}{a^{d}} = \log_{a} a^{c - d} = c - d

czyli stosując przyjęte oznaczenia

\log_{a} \frac{x}{y} = \log_{a} x - \log_{a} y

To kończy dowód.

RYSVciSctKUBy1

Przykład 4

Wykażemy, że

$\log_{16} 2 - \log_{16} 32 = - 1$ .
$\log_{49} 343 - \log_{49} \frac{1}{7} = 2$ .
$\log_{4} 192 - \log_{4} 3 = 3$ .
$\log 1750 - \log \frac{7}{40} = 4$ .

Rozwiązanie:

Korzystamy z twierdzenia o logarytmie ilorazu.

$\log_{16} 2 - \log_{16} 32 = \log_{16} \frac{2}{32} = \log_{16} \frac{1}{16} = \log_{16} 16^{- 1} = - 1$ .
$\log_{49} 343 - \log_{49} \frac{1}{7} = \log_{49} \frac{343}{\frac{1}{7}} = \log_{49} (343 \cdot 7) = \log_{49} 2401 = \log_{49} 49^{2} = 2$ .
$\log_{4} 192 - \log_{4} 3 = \log_{4} \frac{192}{3} = \log_{4} 64 = \log_{4} 4^{3} = 3$ .
$\log 1750 - \log \frac{7}{40} = \log \frac{1750}{\frac{7}{40}} = \log (1750 \cdot \frac{40}{7}) = \log 10000 = \log 10^{4} = 4$ .

Logarytm potęgi

Przykład 5

Wykażemy, że $\log_{5} 8 = 3 \log_{5} 2$ .

Oznaczmy $c = \log_{5} 2$ . Korzystając z definicji logarytmu, otrzymujemy $5^{c} = 2$ . Zatem

\log_{5} 8 = \log_{5} 2^{3} = \log_{5} {(5^{c})}^{3} = \log_{5} 5^{3 \cdot c} = 3 \cdot c = 3 \log_{5} 2

W ten sposób dowód został zakończony.

Logarytm potęgi

Twierdzenie: Logarytm potęgi

Przy dodatniej i różnej od $1$ podstawie $a$ dla dowolnej liczby $x > 0$ prawdziwa jest równość

\log_{a} x^{r} = r \cdot \log_{a} x

Dowód

Oznaczmy $c = \log_{a} x$ . Korzystając z definicji logarytmu, otrzymujemy $a^{c} = x$ . Zatem

\log_{a} x^{r} = \log_{a} {(a^{c})}^{r} = \log_{a} a^{r \cdot c} = r \cdot c

Stosując przyjęte oznaczenia, mamy

\log_{a} x^{r} = r \cdot \log_{a} x

To kończy dowód.

RNWxQ9UHW4Uyw1

Przykład 6

Wykażemy, że

$\log_{5} 16 = 4 \log_{5} 2$ .
$\log 81 = 4 \log 3$ .
$\log_{3} \frac{1}{7} = - \log_{3} 7$ .
$\log_{6} 0, 04 = - 2 \log_{6} 5$ .

Rozwiązanie:

Korzystamy z twierdzenia o logarytmie potęgi.

$\log_{5} 16 = \log_{5} 2^{4} = 4 \log_{5} 2$ .
$\log 81 = \log 3^{4} = 4 \log 3$ .
$\log_{3} \frac{1}{7} = \log_{3} 7^{- 1} = - 1 \cdot \log_{3} 7 = - \log_{3} 7$ .
$\log_{6} 0, 04 = \log_{6} \frac{4}{100} = \log_{6} \frac{1}{25} = \log_{6} 5^{- 2} = - 2 \log_{6} 5$ .