E‑book - Badania laboratoryjne przetworów papierniczych

R2m8fMM6St98o

Grafika otwierająca e‑book. Pod zdjęciem przedstawiającym naczynia laboratoryjne znajduje się tytuł e‑booka "Badania laboratoryjne". Pod nim zaś dalsze informacje: "E‑materiał Badania laboratoryjne wykonywane podczas wytworów papierniczych. Dla kwalifikacji DRM.07. Przetwórstwo wytworów papierniczych wyodrębnionej w zawodzie Technik papiernictwa 311601. Konsultacja: Jakub Brózdowski".

Spis treści

• 1. Zarządzanie jakością11. Zarządzanie jakością

• 2. Narzędzia systemu zarządzania jakością22. Narzędzia systemu zarządzania jakością

  • 2.1. Arkusz analityczny2.12.1. Arkusz analityczny

  • 2.2. Diagram Ishikawy2.22.2. Diagram Ishikawy

  • 2.3. Diagram Pareto‑Lorenza2.32.3. Diagram Pareto‑Lorenza

  • 2.4. Histogram2.42.4. Histogram

  • 2.5. Karty kontrolne Shewharta2.52.5. Karty kontrolne Shewharta

  • 2.6. Schemat blokowy2.62.6. Schemat blokowy

  • 2.7. Wykres korelacji2.72.7. Wykres korelacji

• 3. Karta charakterystyki substancji niebezpiecznych (MSDS)33. Karta charakterystyki substancji niebezpiecznych (MSDS)

• 4. Kontrola jakości44. Kontrola jakości

• 5. Normalizacja55. Normalizacja

  • 5.1. Cele normalizacji5.15.1. Cele normalizacji

  • 5.2. Definicja normy i jej rodzaje5.25.2. Definicja normy i jej rodzaje

  • 5.3 Budowa normy na podstawie normy badań5.35.3 Budowa normy na podstawie normy badań

  • 5.4. Cechy normy5.45.4. Cechy normy

• 6. Błędy pomiaru i ich rodzaje66. Błędy pomiaru i ich rodzaje

• 7. Podstawy statystyki w interpretacji wyników pomiarów77. Podstawy statystyki w interpretacji wyników pomiarów

• 8. Netografia i bibliografia88. Netografia i bibliografia

1. Zarządzanie jakością

Zarządzanie jakością jest ważnym elementem procesu zarządzania całym przedsiębiorstwem. Wdrożenie odpowiedniego systemu służącego zarządzaniu jakością pozwala firmie świadczyć usługi na poziomie zgodnym z oczekiwaniami klienta oraz usprawnić działanie przedsiębiorstwa. System zarządzania jakością składa się z licznych instrumentów, które umożliwiają nadzorowanie procesów produkcyjnych oraz szybką diagnozę i identyfikację źródeł powstawania błędów, co wpływa korzystnie na funkcjonowanie firmy. Systemy zarządzania jakością są narzędziami do identyfikacji wszystkich działań występujących w ciągu produkcyjnym i – poprzez analizę występujących w nim problemów jakościowych – umożliwiają ustalenie miejsc powstawania błędów oraz ich struktury i ważności pod kątem oczekiwań klienta co do jakości gotowego wyrobu.

• Powrót do spisu treścisPowrót do spisu treści

2. Narzędzia systemu zarządzania jakością

Wśród narzędzi systemu zarządzania jakością wyróżnia się m.in.:

• arkusz analityczny,

• diagram Ishikawy,

• diagram Pareto‑Lorenza,

• histogram,

• karty kontrolne Shewharta,

• schemat blokowy DMAIC,

• wykres korelacji.

• Powrót do spisu treścisPowrót do spisu treści

2.1. Arkusz analityczny

R5b3Y5924WLLm

Grafika przedstawia arkusz analityczny w formie tabeli. Składa się ona z trzech głównych kolumn i ośmiu wierszy. Pierwsza kolumna nosi tytuł „Czynności operatora wykonywane na stanowisku X”, druga ma tytuł „Wymagana wartość”, trzecia kolumna nosi tytuł „Numer skontrolowanej sztuki i zmierzone wartości”, dodatkowo umieszczono w niej napis w nawiasie kwadratowym „OK” lub „NOK”. Kolumnę trzecią podzielono na sześć dodatkowych kolumn o tytułach 1, 10, 100, 200, 500, 800. Z tabeli można odczytać następujące dane: dla czynności pierwszej wymagana wartość wynosi 260 plus minus 2 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numerów 1, 10, 100, 200, 500, 800 wartość 260. Dla czynności drugiej wymagana wartość wynosi 6,5 plus 0,3 minus 0 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numerów 1, 10, 100, 800 – wartość 6,5, dla numeru 200 – wartość 6,6, zaś dla numeru 500 wartość 6,7. Dla czynności trzeciej wymagana wartość wynosi 88 plus minus 1 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numerów 1, 10, 100, 500, 800 wartość 88, zaś dla numeru 200 wartość 85 (zaznaczona w tabeli na czerwono). Dla czynności czwartej wymagana wartość wynosi 80 plus minus 1 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numerów 1, 10, 500, 800 wartość 80, dla numeru 100 wartość 79, zaś dla numeru 200 wartość 77 (zaznaczona w tabeli na czerwono). Dla czynności piątej wymagana wartość wynosi 22 plus 0,5 minus 0 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numeru 1 wartość 22,5, zaś dla numerów 10, 100, 200, 500, 800 – wartość 22. Dla czynności szóstej wymagana wartość wynosi 10 plus 0,5 minus 0 mm, natomiast numer skontrolowanej sztuki i zmierzone wartości wynoszą: dla numeru 1 wartość 10,5, zaś dla numerów 10, 100, 200, 500, 800 – wartość 10.

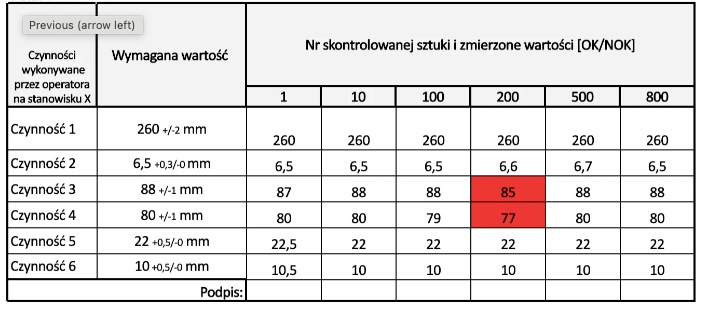
Arkusz analityczny – inaczej nazywany również kartą kontrolną. W arkusz wpisuje się dane o działaniach podjętych w celu produkcji badanego wyrobu lub procesu. Zamieszczane są w nim informacje o zajściu danego zdarzenia, częstotliwości i miejscu jego występowania. Dzięki zebranym danym możliwe są odpowiedzi na pytania typu: Czy wystąpił interesujący nas problem? Jak często występuje? Gdzie pojawia się dany błąd? Jakie konsekwencje powoduje jego zaistnienie?

• Powrót do spisu treścisPowrót do spisu treści

2.2. Diagram Ishikawy

Diagram Ishikawy – bywa też nazywany diagramem rybiej ości, ze względu na swój specyficzny kształt, przypominający szkielet ryby (patrz rysunek 1).

RgWkhuS4dCKLt

Grafika przedstawia diagram Ishikawy – nazywany diagramem rybiej ości, ze względu na swój specyficzny kształt, przypominający szkielet ryby. Jest to diagram przyczynowo skutkowy, który w formie graficznej przedstawia powiązania pomiędzy wpływającymi na proces czynnikami a skutkami ich oddziaływania. Pozwala na zlokalizowanie w procesie miejsc, w których mogą wystąpić problemy. W tym przypadku na grafice w miejscu rybiego ogona umieszczono napis „Czynniki wpływające”, w miejscu rybiej głowy napis „Problem”, te dwa miejsca łączy linia pozioma. Od tej linii odchodzą na boki linie ukośne, niczym rybie ości. Do linii ukośnych przyporządkowano następujące napisy: powyżej linii poziomej „Człowiek”, „Maszyna”, „Metoda”, poniżej linii poziomej napisy: „Materiał”, „Środowisko” lub „Zarządzanie” oraz „Pomiar”.

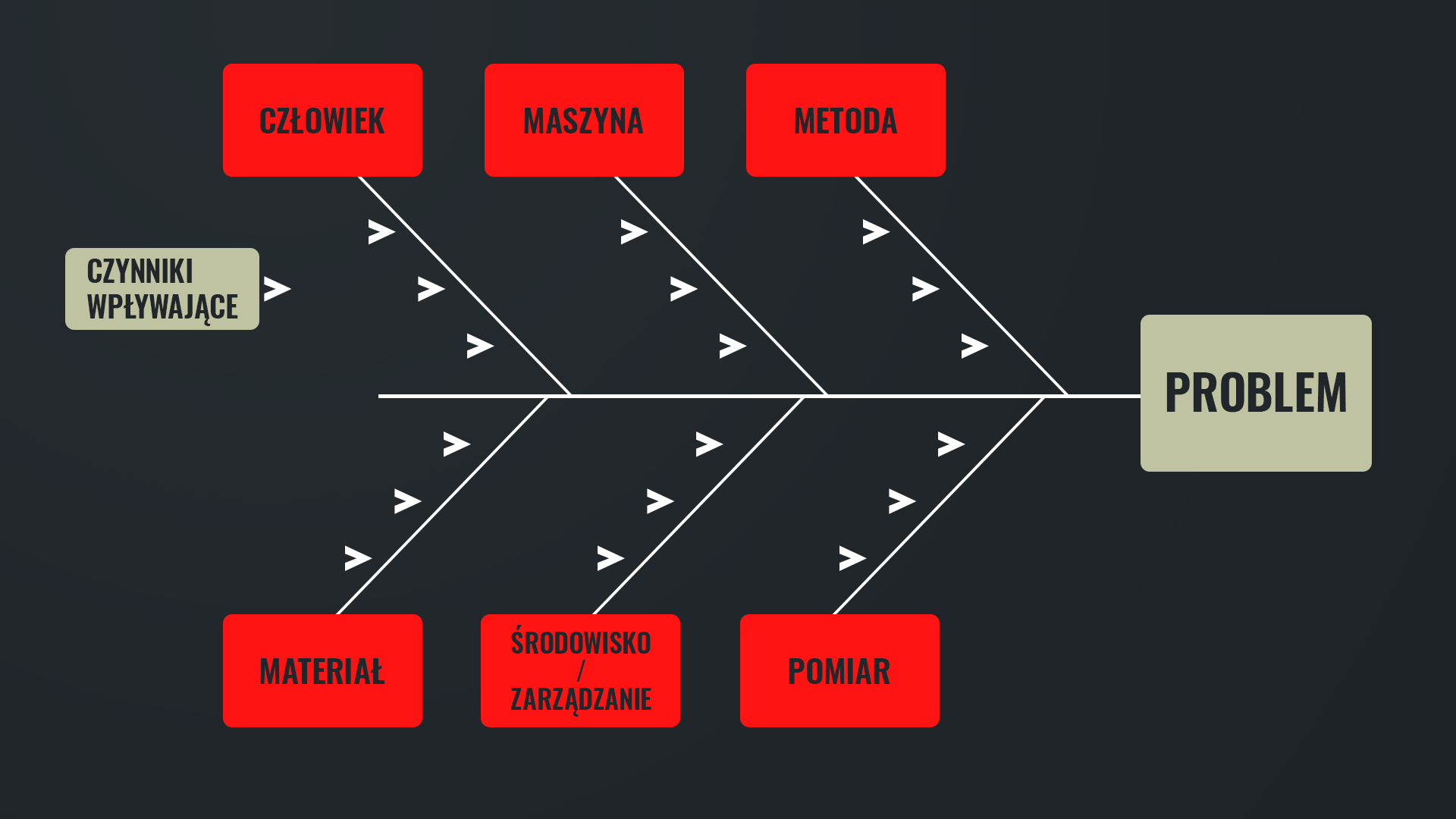
Jest to diagram przyczynowo‑skutkowy, który w formie graficznej przedstawia powiązania pomiędzy wpływającymi na proces czynnikami a skutkami ich oddziaływania. Pozwala na zlokalizowanie w procesie miejsc, w których mogą wystąpić problemy. Diagram Ishikawy powstaje najczęściej podczas tzw. burzy mózgów (ang. brainstorm). Opracowuje się go w trzech etapach.

W pierwszym etapie określa się najważniejsze grupy czynników oddziałujących na wynik procesu, czyli produkt końcowy. W celu określenia grup czynników stosuje się podejście 6‑M – z angielskiego: man, machine, method, material, management/environment, measurement. Tłumacząc na polski: człowiek, maszyna, metoda, materiał, zarządzanie i środowisko oraz pomiar. Grupy czynników dobiera się każdorazowo do występującego problemu.

W drugim etapie do każdej z grup głównych przypisuje się czynniki drugorzędne, które są rozwinięciem czynników/grup głównych. W razie potrzeby można rozwijać czynniki drugorzędne dopisując do nich trzeciorzędne itd.

W etapie trzecim wybiera się czynnik krytyczny, który najsilniej oddziałuje na wynik/produkt rozpatrywanego procesu. W celu wyłonienia czynnika krytycznego można zastosować np. diagram Pareto‑Lorenza.

• Powrót do spisu treścisPowrót do spisu treści

2.3. Diagram Pareto‑Lorenza

RwPHuqKNC9F4Q

Grafika przedstawia diagram Pareto‑Lorenza przyjmującego formę wykresu. Zbudowany jest on z dwóch pionowych osi oraz łączącej je linii poziomej. Pionowa oś po lewej stronie jest opisana jako liczba błędów, widnieje na niej podziałka od 0 do 16 w odstępach co dwa. Pionowa oś po prawej stronie jest opisana jako udział procentowy, widnieje na niej podziałka od 0 do 100 w odstępach co dwadzieścia pięć. Osie są ze sobą połączone w punktach zero linią poziomą opisaną jako przyczyny. Na diagramie widać przykład pięciu słupków ilustrujących dane we wskazanych zakresach. Najwyższy słupek ilustruje następujące wartości: 15 błędów, co oznacza około dziewięćdziesięcioprocentowy udział, natomiast najniższy słupek oznacza 2 błędy oraz około piętnastoprocentowy udział. Na diagramie zaznaczono również przerywaną linią około osiemdziesięcioprocentowy udział, linia łączy dwie pionowe osie. Widać także krzywą przechodzącą przez pierwszy i drugi słupek.

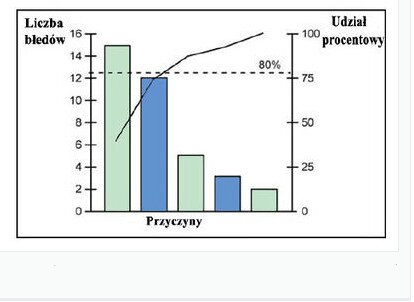
Diagram Pareto‑Lorenza – buduje się na podstawie dowiedzionej doświadczalnie prawidłowości, że 20‑30% przyczyn/czynników jest odpowiedzialnych za 70‑80% skutków. Zidentyfikowanie tych przyczyn pozwala wyznaczyć kierunki działań, które mogą znacząco usprawnić proces i przyczynić się do podniesienia jakości gotowych wyrobów. Diagram wykonuje się w kilku etapach:

etap 1. – zbieranie informacji związanych z występującym w procesie problemem;

etap 2. – wybranie metody pomiaru wielkości wyniku w aspekcie danego procesu;

etap 3. – uszeregowanie przyczyn powstawania problemu ze względu na ich siłę oddziaływania na proces;

etap 4. – obliczenie skumulowanych wartości procentowych dla każdej przyczyny;

etap 5. – połączenie za pomocą linii punktów wartości skumulowanych;

etap 6. – analizowanie wykresu w celu wyłonienia przyczyn, które należy zbadać i wyeliminować w pierwszej kolejności.

• Powrót do spisu treścisPowrót do spisu treści

2.4. Histogram

R83vWpJB4SZTU

Grafika przedstawia histogram przyjmujący formę wykresu słupkowego umieszczonego na osi współrzędnych. Wysokość słupków opisuje liczebność danej cechy, a podstawa wyznacza przedział klasowy. Pionowa oś rzędnych zawiera podziałkę z wartościami od zera do dwudziestu pięciu co pięć. Pozioma oś odciętych przedstawia wartości od minus trzech do trzech zaznaczone co jeden.

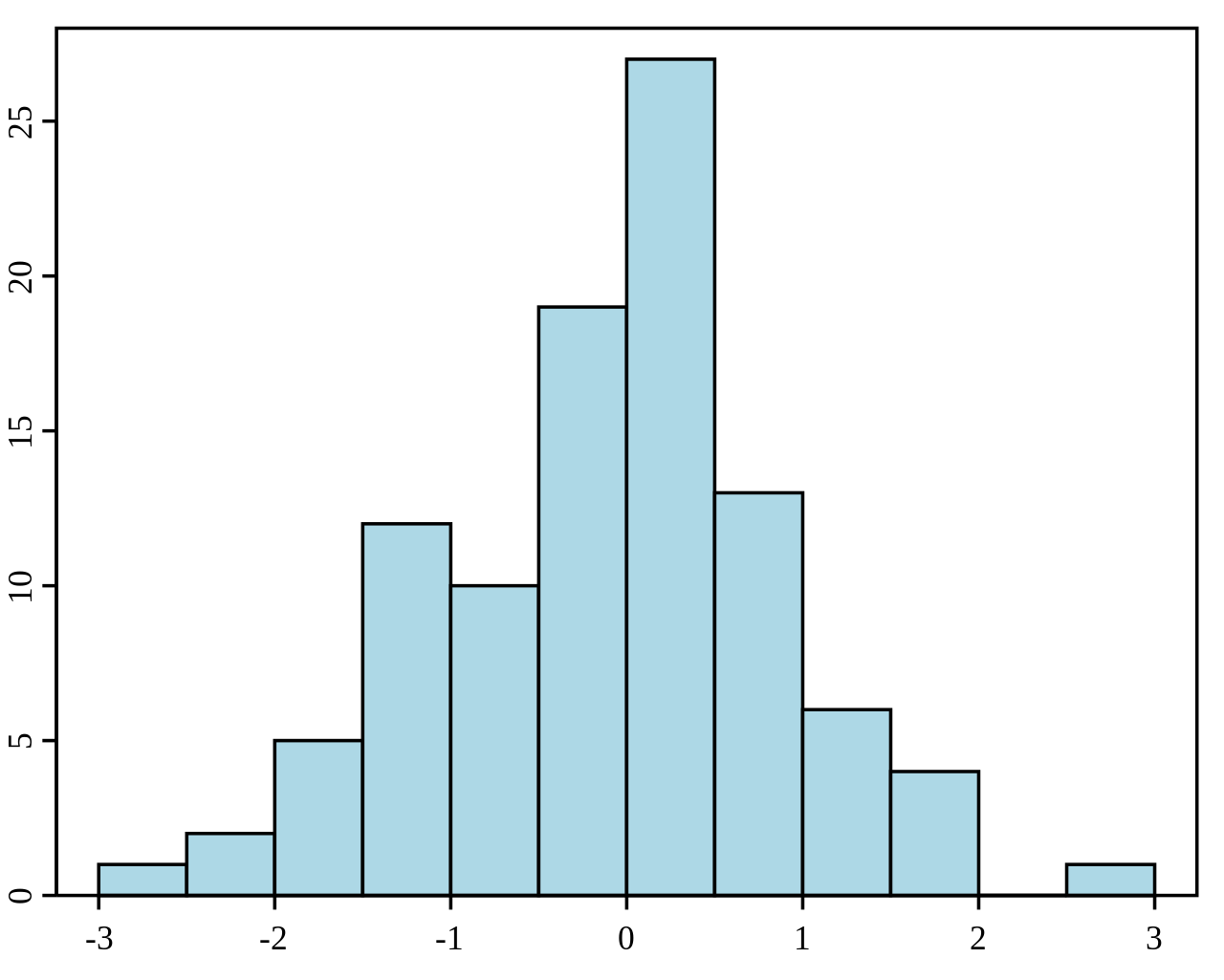
Histogram – jest to wykres słupkowy, który często stosuje się w statystyce w celu graficznego przedstawienia częstotliwości, z jaką występuje dana wartość badanej zmiennej w z góry określonym przedziale. W celu wykreślenia histogramu należy: 1. określić przedział wartości analizowanej wielkości; 2. wyznaczyć liczbę przedziałów w szeregu rozdzielczym – liczba ta powinna wynosić od 5 do 25.

Nie powinno się wykreślać histogramów, w których znajdują się przedziały puste, w przypadku ich wystąpienia należy zredukować liczbę przedziałów.

• Powrót do spisu treścisPowrót do spisu treści

2.5 Karty kontrolne Shewharta

R23AvDyOL7yqp

Grafika, przedstawiająca karty kontrolne Shewharta, składa się z pięciu poziomych linii. Na samej górze widnieje linia ciągła i napis: „GLK (UCL)”, poniżej linia przerywana „GLO”, kolejna to linia drobno przerywana „LC”, przerywana „DLO”, ciągła „DLK (LCL)”. Ostatnia linia jest wzbogacona o przedziałkę 1‑9 (w odstępach co jeden). Pod wykresem widnieje napis” „Numer próbki”. Sam wykres przedstawia łamaną kreskę z punktami kontrolnymi.

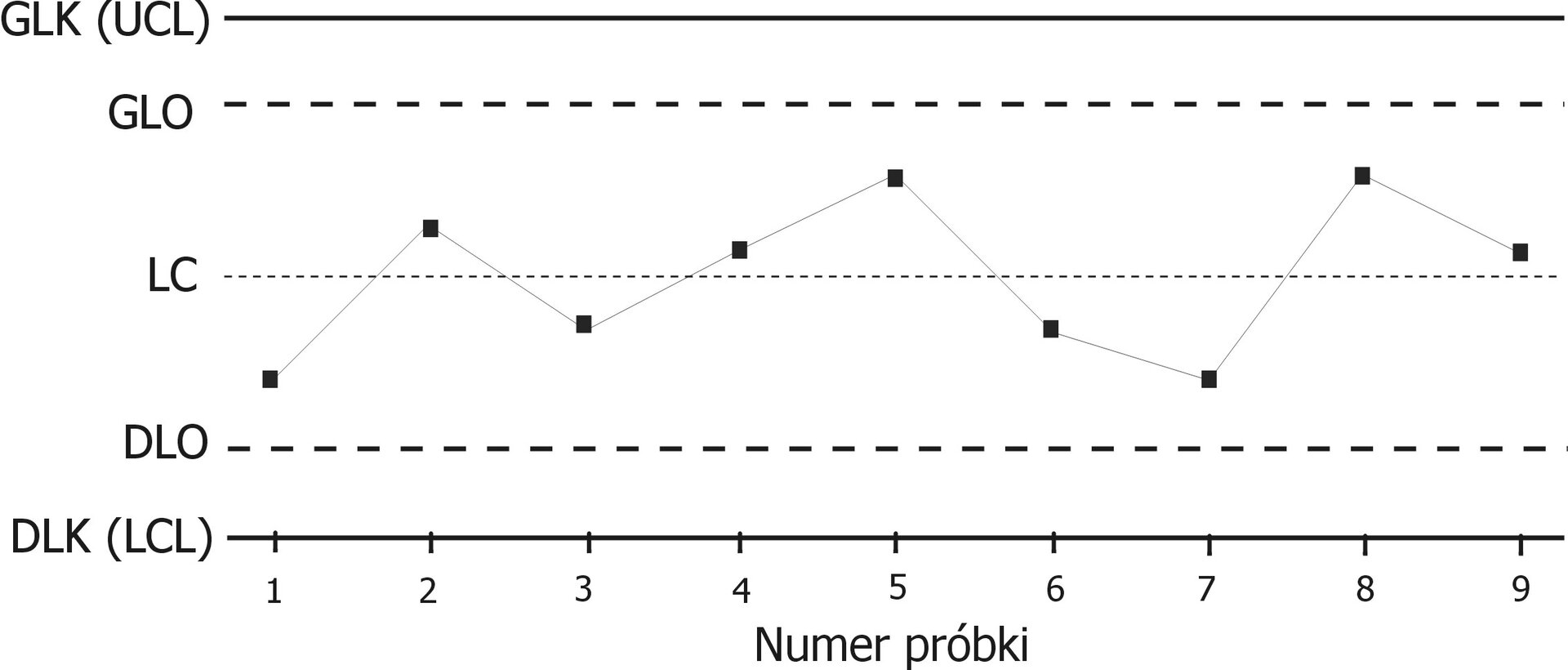
GLK (UCL) - Górna linia kontrolna

GLO - Górna linia ostrzegania

LC - linia centralna

DLO - Dolna linia ostrzegania

DLK (LCL) - Dolna linia kontrolna

Karty kontrolne Shewharta – jest to narzędzie statystyczne stosowane najczęściej, gdy mamy do czynienia z produkcją seryjną. W karcie wpisuje się podstawowe dane statystyczne z badań próbek pobieranych w regularnych odstępach czasu. Dane statystyczne wybranej cechy próbki to np. średnia arytmetyczna, rozstęp, mediana czy odchylenie standardowe. Karta pozwala sprawdzić, czy wybrane parametry mieszczą się w granicach ustalonych dla badanej cechy.

• Powrót do spisu treścisPowrót do spisu treści

2.6. Schemat blokowy

RRZj1xrEglEv6

Grafika przedstawia Schemat technologiczny zawierający operacje i etapy procesów przetwarzania wytworów papierniczych podczas produkcji tektury falistej pięciowarstwowej. Jest to przykład schematu blokowego. Nazwy kolejnych etapów zostały umieszczone w wyróżnionych ramkach. Na ich kolejność wskazują strzałki łączące poszczególne ramki. Pierwszy etap to „Wprowadzanie flutingu - papieru na warstwę pofalowaną między wały ryflujące w celu uzyskania warstwy pofalowanej”. Po obu stronach tej ramki widnieją dwie strzałki skierowane w jej kierunku, nad jedną znajduje się napis „temperatura”, a nad drugą „nawilżanie”. Poniżej kolejna ramka z tekstem: „Naniesienie kleju na wierzchołki fali”, pod nią następna o treści „Przyklejenie lineru do flutingu, przepuszczenie ich między wałami dociskowymi i ryflowanym. Tektura dwuwarstwowa”. Po jego lewej stronie widnieje pozioma strzałka z grotem skierowanym w ramkę, podpisana „Temperatura”. Poniżej znajduje się kolejna ramka, również połączona pionową strzałką, treść napisu w ramce: „Transport dwuwarstwowej tektury falistej specjalnym mostem do sklejarki podwójnej. Nakładanie kleju na odkryte grzbiety fal warstwy pofalowanej.". Od ramki tej odchodzi pionowa strzałka z napisem „stół grzewczo‑suszący”. Strzałka prowadzi do kolejnej ramki „Wprowadzenie drugiego lineru – papieru na drugą warstwę płaską (zewnętrzną)". Nad poziomą strzałką prowadzącą do następnej ramki widnieje napis „stół grzewczo‑suszący”. Treść następnej ramki: „Sklejenie tektury falistej dwuwarstwowej z drugim linerem. Utrwalanie spoin klejowych. Wytworzenie tektury falistej trzywarstwowej.”. Następnie ramka o treści: „Wprowadzanie drugiego flutingu - papieru na warstwę pofalowaną między wały ryflujące w celu uzyskania warstwy pofalowanej. Sklejenie kolejnego lineru z warstwą pofalowaną między wałem dociskowym i ryflowanym. Wytworzenie drugiej tektury falistej dwuwarstwowej.”. Ramka ta jest połączona poziomą strzałką, nad którą znajduje się napis „stół grzewczo‑suszący”. Treść ostatniej ramki: „Sklejenie ze sobą tektury falistej trzywarstwowej z tekturą falistą dwuwarstwową. Wytworzenie tektury falistej pięciowarstwowej.".

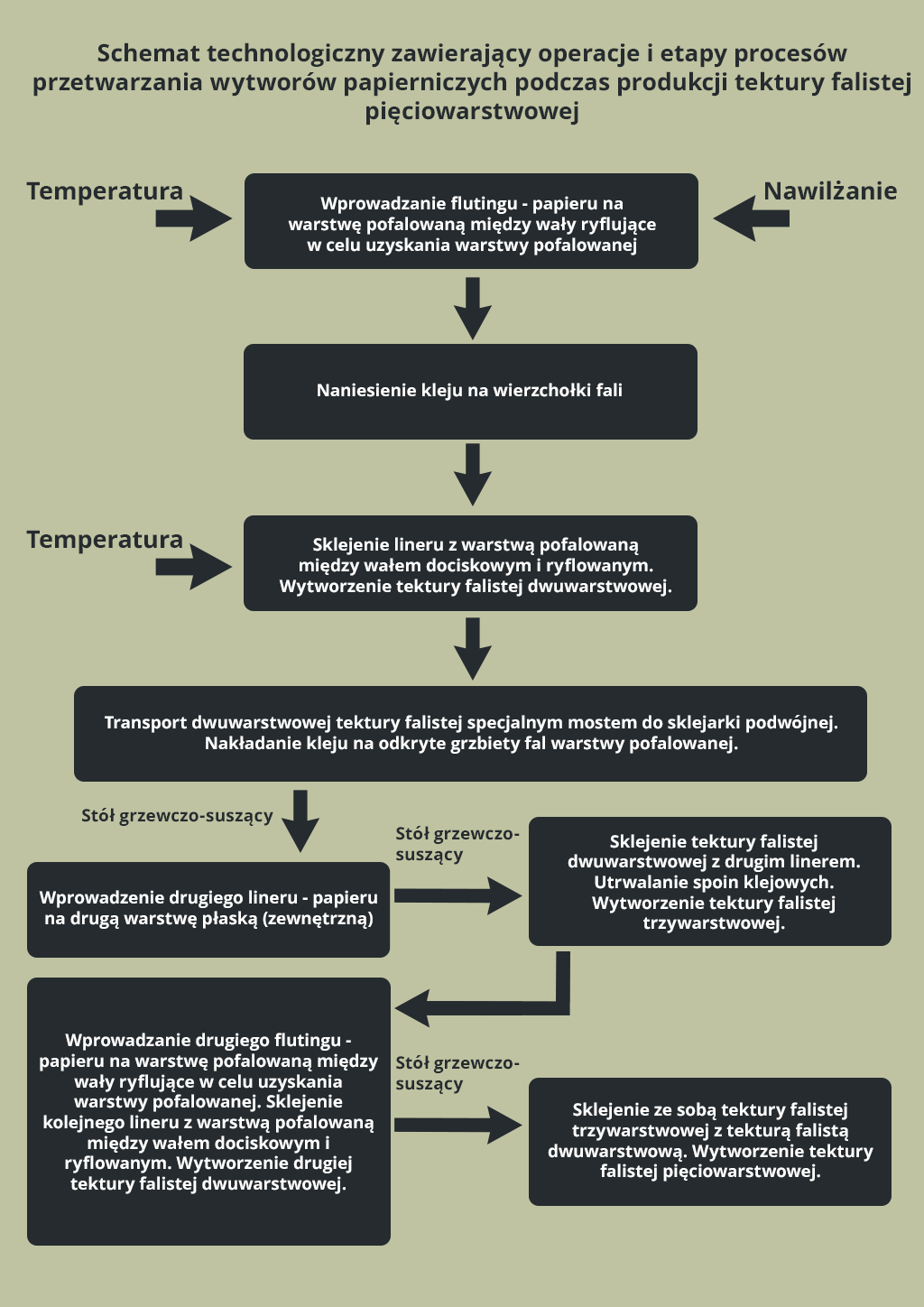
Schemat blokowy – jest to graficzne przedstawienie działań podejmowanych w badanym procesie. Tworzenie schematu pozwala zwrócić uwagę na powiązania pomiędzy różnymi działaniami, które w samym procesie są mało widoczne. Schemat powinno się tworzyć w postaci kolumnowej, gdzie zadania najistotniejsze dla procesu są zaznaczane w kolumnie głównej, a działania pomocnicze wrysowuje się w postaci pętli czy odsyłaczy.

• Powrót do spisu treścisPowrót do spisu treści

2.7. Wykres korelacji

RqbOh6vPODStv

Grafika przedstawia wykres korelacji, po lewej stronie, pionowo, w przedziale n‑100 (w odstępach co dwadzieścia, widnieje „Zawartość części nierozwłóknionych %”, zaś poziomo, z przedziałką n‑120 (w odstępach co dwadzieścia) „Czas obróbki min”. Sam wykres przyjmuje formę krzywej; przy zawartości 100% części nierozwłóknionych – czas obróbki wynosi 0 minut, przy 80% - 20 minut, przy 60% - 40 minut, przy 40% - 60 minut, 20% - 80 minut, pomiędzy 0 a 20% - 100 minut, 0% - 120 minut.

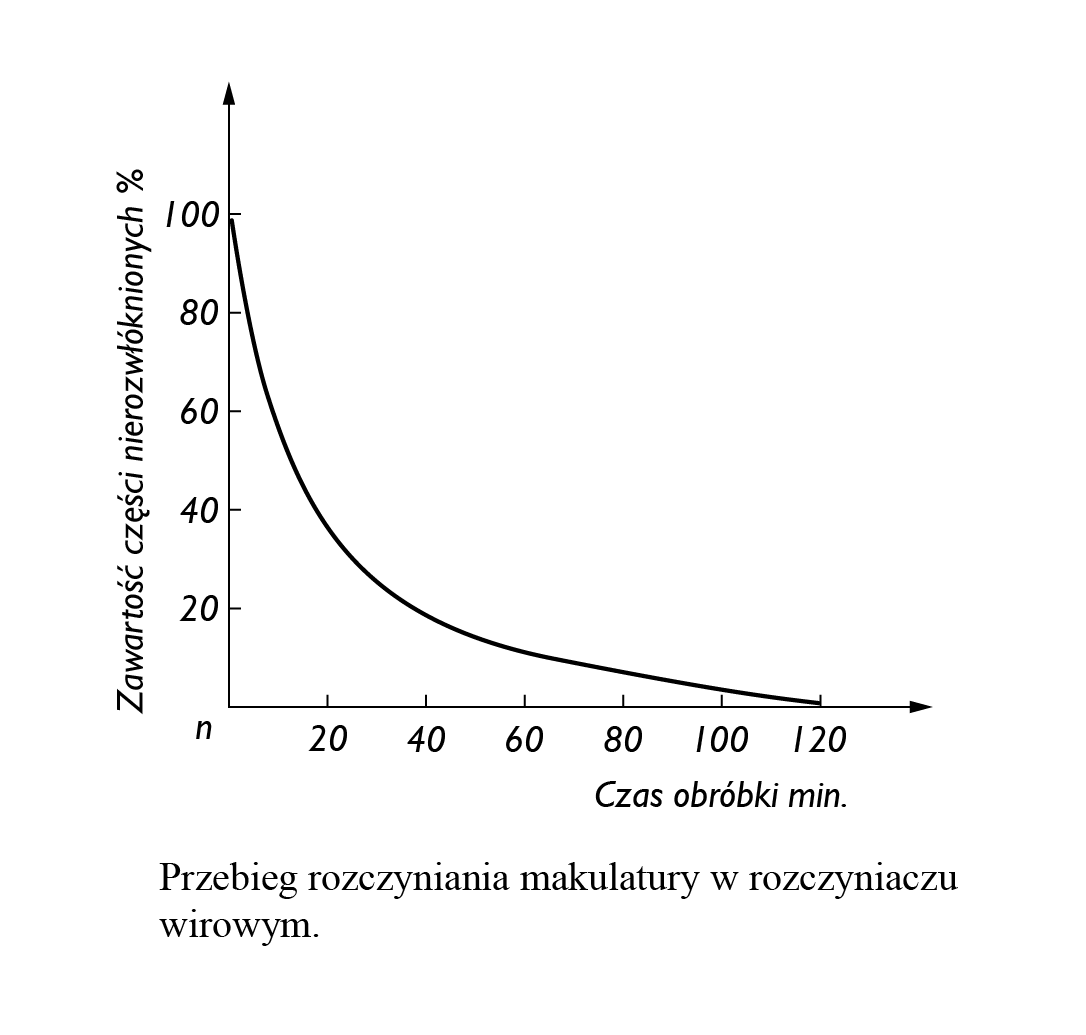
Wykres korelacji – jest graficznym przedstawieniem związku między dwiema badanymi zmiennymi, pokazującym zależności przyczynowo‑skutkowe. W celu stworzenia wykresu korelacji powinno się dysponować co najmniej 30 danymi. Wykres kreśli się przez nanoszenie pary wyników na siatkę współrzędnych XY. Gdy naniesione punkty tworzą krzywą nachyloną do osi poziomej, mówimy o ich korelacji, a gdy są rozproszone lub powstająca krzywa jest prostopadła do osi Y, mówimy o braku korelacji pomiędzy zmiennymi.

Gdy krzywa odchylona jest do góry, mówimy o dodatnim współczynniku korelacji, a jeśli nachylona jest w dół, mamy do czynienia z ujemnym współczynnikiem korelacji.

• Powrót do spisu treścisPowrót do spisu treści

3. Karta charakterystyki substancji niebezpiecznych (MSDS)

Dokument zawierający opis podstawowych właściwości fizykochemicznych danej substancji niebezpiecznej lub mieszaniny. Wymienia zagrożenia, jakie substancja może powodować, metody zapobiegania zagrożeniom oraz procedury, według których należy postąpić w przypadku skażenia daną substancją.

Karta MSDS (ang. Material Safety Data Sheet) składa się z 16 sekcji. Poszczególne sekcje opisują substancję, identyfikują związanie z nią zagrożenia, informują o składzie, wymieniają środki pierwszej pomocy, opisują procedury postępowania w przypadku pożaru i uwolnienia substancji do środowiska. Karta MSDS wskazuje na postępowanie oraz magazynowanie substancji/mieszaniny, kontrolę narażenia i środki ochrony indywidualnej. Karta opisuje właściwości fizyczne i chemiczne substancji lub mieszaniny oraz jej stabilność i reaktywność. Zawiera informacje toksykologiczne i ekologiczne. Wyjaśnia procedurę postępowania z odpadami. Dostarcza informacji o transporcie substancji oraz o obowiązujących w nim przepisach prawnych. Ostatnia sekcja karty charakterystyki substancji niebezpiecznych wskazuje informacje, które uległy zmianie od czasu wydania poprzedniej wersji karty.

R2dniXa4xW2l8

Grafika przedstawia pierwszą stronę przykładowej karty charakterystyki substancji niebezpiecznej. Na samej górze widnieje tytuł, po prawej: "Data utworzenia" oraz "Data aktualizacji". Poniżej informacja, że jest to Sekcja 1. oraz tytuł tejże" "Identyfikacja substancji mieszaniny i identyfikacja przedsiębiorstwa". Pod tytułem sekcji widnieje punkt 1.1. "Identyfikator produktu", na który składa się "Nazwa produktu", "Nr katalogowy", "Typ produktu", "Wzór chemiczny". Części te widoczne są po lewej stronie karty, po prawej zaś - dane. Punkt 1.2 to "Istotne zidentyfikowane zastosowania substancji lub mieszaniny oraz zastosowania odradzane". Poniżej zaś: "Zastosowania zidentyfikowane" oraz "Zastosowania odradzane". Części te widoczne są po lewej stronie karty, po prawej zaś - dane. Punkt 1.3 to "Dane dotyczące dostawcy karty charakterystyki", poniżej zaś napis: "Przedsiębiorstwo" oraz "Numer telefonu kontaktowego". Punkt 1.4 to "Numer telefonu alarmowego", poniżej zaś powtórzona treść. Po prawej stronie widnieją dane. Sekcja 2 zatytułowana jest "Identyfikacja zagrożeń". Punkt 2.1 "Klasyfikacja substakcji lub mieszaniny", poniżej punktu widnieje opis oraz odesłanie do innej sekcji. Punkt 2.2 to "Elementy oznakowania". Poniżej znajduje się tabela zbudowana z dwóch kolumn oraz czterech wersów. W pierwszej kolumnie w pierwszym wierszu widnieje napis "Piktogramy zagrożenia", w drugim wierszu "Hasło ostrzegawcze", w trzecim "Zwroty wskazujące rodzaj zagrożenia", w czwartym "Zwroty wskazujące środki ostrożności". Druga kolumna i przypisane do niej wiersze zawierają dane. Punkt 2.3 to "Inne zagrożenia". Poniżej znajduje się opis.

• Powrót do spisu treścisPowrót do spisu treści

4. Kontrola jakości

Kontrola jakości – jest działaniem w celu skontrolowania (np. zmierzenia czy sprawdzenia) jednej lub kilku cech danego produktu. Po zmierzeniu danej cechy należy ją porównać do wymagań i w ten sposób określić, czy dany parametr produktu spełnia je i produkt może zostać dostarczony do odbiorcy. Badanymi parametrami może być np. gramatura, grubość, połysk, białość.

Możemy wyróżnić sześć rodzajów kontroli jakości:

1. Kontrola wejściowa – której poddajemy kupione półprodukty, surowce; to np. sprawdzenie parametrów papieru, który zostanie wykorzystany do produkcji tektury falistej czy zbadanie właściwości klejów.

2. Kontrola międzyoperacyjna – która ma na celu sprawdzenie poprawności przebiegu poszczególnych etapów procesu produkcji. Stosuje się ją, gdy podejrzewamy, że któryś etap produkcji powoduje wadę produktu gotowego, np. tępy nóż uszkadza brzegi gotowego kartonu.

3. Kontrola końcowa – której poddajemy gotowy produkt końcowy. Kontrola obejmuje sprawdzenie właściwości wizualnych i mechanicznych, np. jakość nadruku, odporność na zgniatanie.

4. Kontrola ostateczna – której poddawany jest produkt już w trakcie wysyłki do klienta. Kontrola odbywa się na próbkach losowo pobranych z partii; ma na celu potwierdzenie zgodności produktu z zamówieniem oraz poprawności procesu kontroli jakości.

5. Kontrola stuprocentowa – której poddawana jest każdy wyprodukowany produkt.

6. Kontrola statystyczna – polega na kontrolowaniu losowo wybranych produktów i na podstawie ich cech przewidywanie cech całej partii produkcyjnej. Kontrola statystyczna może być przeprowadzana w trakcie lub na koniec cyklu produkcyjnego, dlatego jest nazywana kontrolą wyrywkową. W zależności od wielkości i częstotliwości pobierania próbek oraz sposobu wykorzystania informacji z kontroli do zwrotnego oddziaływania na proces produkcji, kontrola statystyczna może mieć charakter pobranej w sposób losowy próbki.

• Powrót do spisu treścisPowrót do spisu treści

5. Normalizacja

Normalizacja, zgodnie z Ustawą z dnia 12 września 2002 roku, jest to działalność zmierzająca do uzyskania optymalnego, w danych okolicznościach, stopnia uporządkowania w określonym zakresie, poprzez ustalenie postanowień przeznaczonych do powszechnego i wielokrotnego stosowania, dotyczących istniejących lub mogących wystąpić problemów. Tłumacząc na język bardziej zrozumiały: celem normalizacji jest określenie procedur, które będą powszechnie i wielokrotnie stosowane, a dotyczą problemów badanych teraz lub mogących wystąpić w przyszłości. Poprzez normalizację dążymy do zapewniania określonej jakości produktów.

• Powrót do spisu treścisPowrót do spisu treści

5.1. Cele normalizacji

• ogólna oszczędność

• dbanie o interesy użytkownika  

• dbanie o ochronę życia i zdrowia.

Powrót do spisu treścisPowrót do spisu treści

5.2. Definicja normy i jej rodzaje

Norma jest to dokument zawierający przepisy, wzory, wytyczne, określający sposób postępowania. Norma jest przeznaczona do wielokrotnego i powszechnego stosowania.

W zależności od zawartości można podzielić normy na 8 rodzajów:

• normy podstawowe - z ogólnymi postanowieniami dotyczącymi dziedziny, nazywane normami podstawowymi;

• normy terminologiczne - zawierające terminy wraz z definicjami i objaśnieniami;

• normy badań - zawierające metody przeprowadzania badań;

• normy wyrobu - określająca wymagania, jakie spełniać musi określony wyrób w celu zapewnienia funkcjonalności;

• normy usług - określająca wymagania, które powinny być spełnione przez usługę w celu spełnienia jej funkcjonalności

• normy procesu, określające wymagania stanowiące o funkcjonalności procesu;

• normy interfejsu - zawierające wymagania kompatybilności wyrobów w miejscach ich łączenia;

• normy danych – określające cechy i właściwości, które powinny zostać podane w celu określenia wyrobu lub usługi.

Powrót do spisu treścisPowrót do spisu treści

5.3 Budowa normy na podstawie normy badań

Pierwsza strona normy zawiera między innymi jej numer i tytuł.

W treści normy znajduje się wstęp opisujący ogólne założenia normy i jej zakres. Następnie opisane są terminy i definicje stosowane w normie, wymagania stawiane przedmiotowi normy, procedury przygotowania np. urządzeń i odczynników, procedura przeprowadzania badań. Na końcu normy opisany jest sposób raportowania wyników analizy lub badania opisanego w normie.

Przed przystąpieniem do wykonania oznaczenia, analizy lub badania opisanego w normie należy zapoznać się z treścią całej normy, przygotować próbki, odczynniki, niezbędny sprzęt i urządzenia. Po przygotowaniu stanowiska pracy można przystąpić do badania. Należy przestrzegać procedury krok po kroku. Nie można pominąć żadnego punktu opisanego w normie.

Powrót do spisu treścisPowrót do spisu treści

5.4. Cechy normy

• norma jest powszechnie dostępna

• norma jest zaakceptowana przez jednostkę do tego upoważnioną

• norma jest wypracowana na podstawia porozumienia z branżą ją wykorzystującą

• norma jest stosowana dobrowolnie

• norma gwarantuje, że jest zgodna z przepisami

• norma gwarantuje każdemu możliwość uczestniczenia w procesie jej sporządzania

• norma jest wolna od ingerencji w nią organów władzy

Powrót do spisu treścisPowrót do spisu treści

6. Błędy pomiaru i ich rodzaje

Na wynik pomiaru wpływa wiele czynników, np. osoba wykonująca pomiar, przyrząd, z którego korzystamy, otoczenie, w którym dokonujemy pomiaru. Dlatego każdy pomiar obarczony jest błędem pomiaru. Błąd pomiaru jest to odstępstwo pojedynczego wyniku pomiaru od wartości prawdziwej.

Wyróżnia się następujące rodzaje błędów:

Błąd bezwzględny – różnica pomiędzy wartością zmierzoną a wartością rzeczywistą.

$\mathrm{\Delta }x=|x-x_0|$

Gdzie:

Δdeltax – błąd bezwzględny,

x – wartość, jaką zmierzyliśmy,

xIndeks dolny 0₀ – wartość rzeczywista, której zazwyczaj nie znamy, można ją wyznaczyć jako średnią z serii pomiarów, jako wynik pomiaru dużo dokładniejszym przyrządem, lub np. obliczyć teoretycznie.

Przykład: Pasek papieru ma długość 120,5 mm. Pomiar wykonany przez uczniów wyniósł 120 mm.

Oblicz błąd bezwzględny i względny pomiaru uczniów.

Błąd bezwzględny pomiaru uczniów:

Δdeltax=|x−xIndeks dolny 0₀|=|120,5−120|=0,5 mm

Błąd względny – iloraz błędu bezwzględnego i wartości rzeczywistej.

${\delta }_x=\frac{\Delta x}{x_0}$

Gdzie:

δdeltaIndeks dolny x_x – błąd względny,

∆x – błąd bezwzględny,

xIndeks dolny 0₀ – wartość rzeczywista.

Błąd względny pomiaru uczniów z powyższego przykładu:

Błąd względny w procentach:

Błąd systematyczny – wynikający z metody, sposobu pomiaru lub urządzenia pomiarowego. Ze względu na pochodzenie błędu wszystkie wyniki uzyskane przez pomiar tą samą metodą, tym samym urządzeniem czy w jednakowy sposób będą miały ten sam błąd systematyczny. Wynik będzie jednakowo zaniżony lub zawyżony.

Błąd przypadkowy – który nie wynika z czynników systematycznych i nie można przewidzieć jego występowania ani wpływu na pomiar. Jego występowanie można zaobserwować porównując ze sobą dużą liczbę wyników.

• Powrót do spisu treścisPowrót do spisu treści

7. Podstawy statystyki w interpretacji wyników pomiarów

Podstawową wartością, którą posługujemy się podczas interpretowania serii wyników, jest średnia arytmetyczna.

Średnia arytmetyczna zbioru liczb to suma tych liczb podzielona przez ich liczbę. Średnia arytmetyczna liczb xIndeks dolny 1₁, xIndeks dolny 2₂, xIndeks dolny 3₃, ... , xIndeks dolny n  Indeks dolny koniec_n  wyraża się wzorem: 

Oblicza się ją przez zsumowanie wartości wszystkich pomiarów. Na przykład sumujemy 5 wyników pomiarów gramatury, a następnie sumę wartości wyników dzielimy przez ich liczbę, w tym przypadku przez 5.

Przykład: wyniki pomiaru gramatury arkusików laboratoryjnych wynoszą: 67,5; 67,3; 68,0; 65,7; 67,9 g/mIndeks górny 2².

$\frac{67,5+67,3+68,0+65,7+67,9}{5}=\frac{336,4}{5}=67,3\frac{g}{m^2}$

Suma wyników pomiaru gramatury wynosi: 336,4, po podzieleniu przez 5 otrzymujemy średnią wartość gramatury: 67,28 g/mIndeks górny 2².

Wynik powinniśmy zaokrąglić do jednego miejsca po przecinku. Patrzymy na drugie miejsce po przecinku; jeżeli cyfra na tym miejscu jest większa lub równa 5, wynik zaokrąglamy o 1 w górę, a jeżeli cyfra na drugim miejscu jest mniejsza od 5, pierwsza cyfra pozostaje bez zmian. W tym przypadku zaokrąglona średnia wartość gramatury badanych arkusików wynosi 67,3 g/mIndeks górny 2².

Innym rodzajem średniej jest średnia ważona. Przy jej obliczaniu do poszczególnych wyników przypisujemy wagi, a następnie wynik obliczamy jak w przypadku średniej arytmetycznej.

XIndeks dolny w_w - średnia ważona

XIndeks dolny 1₁ - liczby, z których liczona jest średnia

WIndeks dolny 1₁ - wagi dla liczb

Przykład: Znamy wyniki dwóch serii pomiarowych odporności na przepuklenie wykonanych na próbkach z tej samej partii produkcyjnej. W pierwszej serii pomiarowej wykonano 7 pomiarów i otrzymano średni wynik odporności na przepuklenie 75 kPa. W drugiej serii wykonano natomiast 10 pomiarów, których średni wynik wyniósł 81 kPa. Średnia arytmetyczna tych dwóch serii pomiarowych wynosi 78 kPa. Jednak w tym przypadku jest to wynik nieprawidłowy, ponieważ średnią z poszczególnych serii powinno się pomnożyć przez wagę w postaci liczby wykonanych pomiarów w każdej z serii i sumę iloczynów podzielić przez liczbę pomiarów . I tak w omawianym przykładzie obliczenie średniej ważonej wygląda następująco:

=78,529 kPa

Po zaokrągleniu otrzymujemy 79 kPa – jak widać, jest to wynik różny od wyników z średniej arytmetycznej wyników dwóch serii pomiarowych.

Kolejną wartością, istotną dla interpretacji wyników, jest odchylenie standardowe. Jest to wartość, o jaką zmieniają się wyniki pomiaru względem wartości średniej. Wzór na odchylenie standardowe

$SD =\sqrt[]{\frac{\sum _{i=1}^n{\left(X-\stackrel{-}{X}\right)}^2}{N-1}}$ , gdzie: 

𝑆𝐷- odchylenie standardowe

$\stackrel{-}{X}$ - Średnia

𝑋 - kolejna obserwacja w próbie

𝑁 - liczba obserwacji w próbie

W omawianym już przypadku pomiarów gramatury, gdzie wyniki wynosiły 67,5; 67,3; 68,0; 65,7; 67,9 g/mIndeks górny 2², odchylenie standardowe wynosi 0,9. Obliczona wcześniej wartość średnia wynosi 67,3 g/mIndeks górny 2². Odchylenie standardowe zapisujemy zazwyczaj razem z wartością średnia i zapis ten wygląda następująco – wynik pomiarów gramatury arkusików wynosi:

67,3 ± 0,8 g/mIndeks górny 2²

RYHvARR8iBSDF

Ilustracja

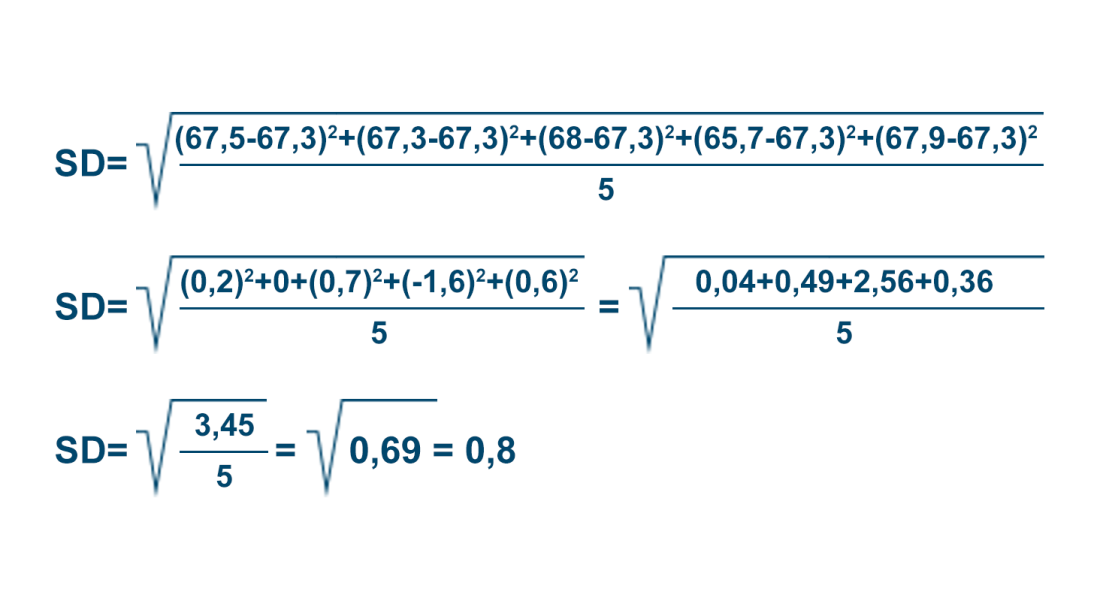
Kolejną z miar stosowanych w statystyce wyników jest  rozstęp, czyli miara rozrzutu. Jest to różnica pomiędzy największą a najmniejszą wartością w badanej serii pomiarowej. W omawianym już przykładzie badania gramatury do obliczenia rozstępu musimy wybrać wartość największą i najmniejszą. Największa zmierzona wartość to 68,0 a najmniejsza to 65,7 g/m2. Rozstęp wyników wynosi więc:

68,0 – 65,7 = 2,3 g/mIndeks górny 2²

Wzór na rozstęp

R= Xmax- Xmin

gdzie: 

R – rozstęp

Xmax – najwyższa wartość w zbiorze

Xmin – najniższa wartość w zbiorze

Wartością istotną w interpretacji wyników jest również mediana.

Mediana – jest to wartość środkowa, w przypadku nieparzystej ilości liczb w zbiorze będzie to liczba środkowa, w przypadku parzystej ilość liczb jest to średnia z dwóch środkowych liczb.

Przykład: 

Dla zbioru liczb: 1, 2, 4, 6, 7 medianą będzie liczba 4 

A dla zbioru liczb 1, 2, 4, 6, 7, 8 medianą będzie średnia liczb 4 i 6, która wynosi 5.   

• Powrót do spisu treścisPowrót do spisu treści

8. Netografia i bibliografia

Netografia:

• Arkusz analityczny, https://mfiles.pl/pl/index.php/Arkusz_analityczny (data dostępu: 31.08.2021).

• Kontrola jakości, https://mfiles.pl/pl/index.php/Kontrola_jakości (data dostępu: 31.08.2021).

• Mydlarz A., Kontrola jakości – o 4 rodzajach kontroli i jak nie przepłacić, https://inzynierjakosci.pl/2018/08/kontrola-jakosci/ (data dostępu: 31.08.2021).

• Normalizacja, https://mfiles.pl/pl/index.php/Normalizacja (data dostępu: 31.08.2021).

• Normy, https://mfiles.pl/pl/index.php/Normy (data dostępu: 31.08.2021).

• Rozporządzenie Komisji (UE) 2020/878 z dnia 18 czerwca 2020 r. zmieniające załącznik II do rozporządzenia (WE) nr 1907/2006 Parlamentu Europejskiego i Rady w sprawie rejestracji, oceny, udzielania zezwoleń i  stosowanych ograniczeń w zakresie chemikaliów (REACH) (Tekst mający znaczenie dla EOG) https://eur-lex.europa.eu/legal-content/PL/TXT/?uri=CELEX:32020R0878 (data dostępu: 31.08.2021).

• Smolarek I., Mielczarek K., Wykorzystanie narzędzi. Zarządzanie jakością w procesie produkcji poligraficznej wybranego opakowania, „Zeszyty Naukowe Quality. Production. Improvement” No 2(7) 2017 http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.baztech-70296410-b9f6-4db6-835b-420a77788650/c/qpi.No.2_7_-13.2017.pdf – Plik PDF o rozmiarze 537 KB w języku polskim -  (data dostępu: 31.08.2021).

• Zarządzanie Jakością - Certyfikacja ISO 9001, https://www.imqpoland.pl/zarzadzanie-jakoscia-iso-9001 (data dostępu: 31.08.2021).

Bibliografia:

• Hamrol A., Manutra W., Zarządzanie jakością teoria i praktyka, Wydawnictwo Naukowe PWN, Warszawa 2002.

• Powrót do spisu treścisPowrót do spisu treści