E‑book - Geodezyjna obsługa obiektów inżynierskich

R1051409VmBVp

Ilustracja przedstawia okładkę e‑booka. Pośrodku, wpisane w koło, widoczne jest zdjęcie teodolitu oraz głowa osoby patrzącej przez wizjer aparatury. Poniżej, na czarnym tle, widoczny jest tytuł e‑booka: Geodezyjna obsługa obiektów inżynierskich. Poniżej widoczny jest napis: E‑zasób: Pomiary realizacyjne i kontrolne. Dla kwalifikacji BUD.18 Wykonywanie pomiarów sytuacyjnych, wysokościowych i realizacyjnych oraz opracowywanie wyników tych pomiarów. Kwalifikacja wyodrębniona w zawodzie technik geodeta 311104.

Spis treści

1. Wstęp1. Wstęp
2. Metoda biegunowa2. Metoda biegunowa
3. Metoda swobodnego stanowiska3. Metoda swobodnego stanowiska
4. Metoda prostej odniesienia4. Metoda prostej odniesienia
5. Metoda rzutowania5. Metoda rzutowania
6. Metoda przestrzennych wcięć kątowych6. Metoda przestrzennych wcięć kątowych
7. Metoda biegunowa 3D7. Metoda biegunowa 3D
8. Metoda trygonometryczna8. Metoda trygonometryczna
9. Metoda dwusiecznych kierunków stycznych9. Metoda dwusiecznych kierunków stycznych
10. Przykład pomiarowy dotyczący wyznaczenia ugięcia i wyboczenia dźwigara10. Przykład pomiarowy dotyczący wyznaczenia ugięcia i wyboczenia dźwigara

1. Wstęp

Geodezyjne pomiary realizacyjne oraz kontrolne wymagają od technika geodety, znajomości metod pomiarowych niezbędnych na etapie realizacji obiektu jak również później w trakcie eksploatacji danego obiektu. W tym opracowaniu przedstawiono wybrane metody pomiarowe służące zarówno tyczeniu obiektów w terenie jak również realizacji pomiarów kontrolnych. Dla każdej z nich oprócz opisu zamieszczono również informację w jakich sytuacjach można ją stosować.

2. Metoda biegunowa

Metoda biegunowa polega na ustawieniu instrumentu, np. tachimetru nad punktem osnowy o znanych współrzędnych. Instrument należy spoziomować oraz wykonać dokładne centrowanie nad punktem osnowy. Następnie w nawiązaniu do punktu osnowy o znanych współrzędnych należy odłożyć kąt oraz odmierzyć odległość do tyczonego punktu.

Powyższy opis dokładnie ilustruje przedstawiony poniżej szkic tyczenia

Stanowiskiem dla metody biegunowej jest w tym przypadku punkt P100 niego są tyczone poszczególne punkty obrysu budynku. Nawiązanie stanowiska stanowi punkt P101. Po dokładnym wycelowaniu na ten punkt należy ustawić odczyt kręgu poziomego (Hz) równy 0. Następnie odkładając kąt oraz odmierzając odległość należy tyczyć poszczególne punkty.

R1W3GyLTHnVif

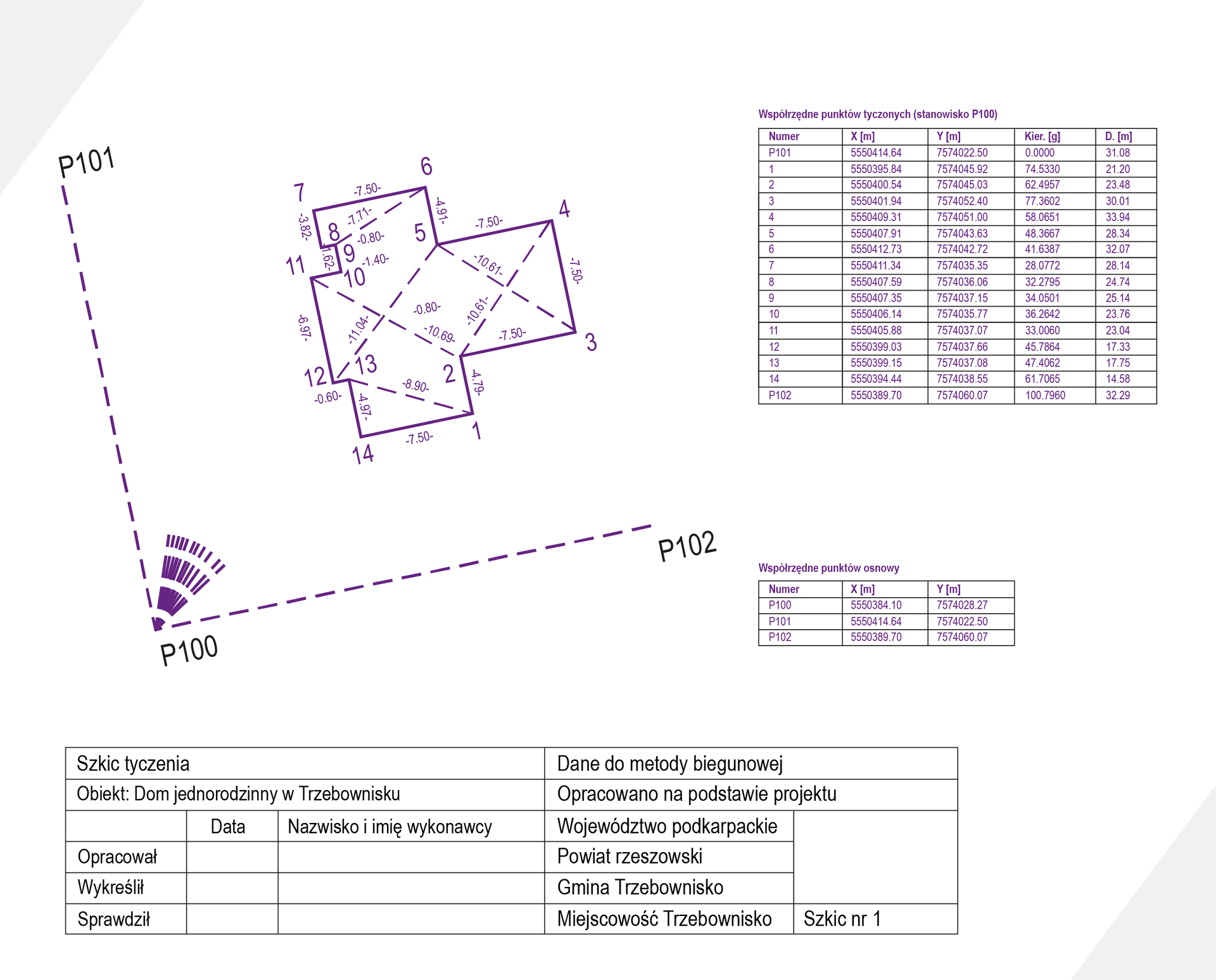
Grafika przedstawia fragment przykładowego szkicu dokumentacyjnego. Po lewej stronie widoczna jest oś współrzędnych z promieniście rozchodzącymi się liniami z narożnika, opisanego jako P100. Oś x opisana jest u góry jako P101. Oś y opisana jest jako P102. Pośrodku osi współrzędnych widoczny jest plan obiektu na planie krzyża. Po prawej stronie u góry i u dołu, widoczne są tabelki. Jedna z nich to współrzędne punktów tyczonych (stanowisko P100), druga to współrzędne punktów osnowy. Poniżej znajduje się tabela z komórkami opisanymi jako: Szkic tyczenia, Dane do metody biegunowej, Obiekt: Dom jednorodzinny w Trzebownisku, Opracowano na podstawie projektu, Data, Nazwisko i imię wykonawcy, Opracował, Wykreślił, Sprawdził, Województwo podkarpackie, Powiat rzeszowski, Gmina Trzebownisko, Miejscowość Trzebownisko, Szkic nr 1.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys 2.1 – Fragment szkicu dokumentacyjnego
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Metoda ta ma szerokie zastosowanie i może być z powodzeniem stosowana w różnorodnych pomiarach realizacyjnych m.in. z zakresu budownictwa ogólnego, budownictwa drogowego.

W tym miejscu należy jednak zwrócić uwagę na ograniczenia wynikające ze stosowania tej metody.

Wymusza ona ustawienie instrumentu w konkretnym miejscu stanowiącym punkt osnowy co w dynamicznym środowisku budowy nie zawsze jest optymalnym rozwiązaniem. Lepsza w takich sytuacjach może się okazać opisana w dalszej części metoda swobodnego stanowiska.

Powrót do spisu treściPowrót do spisu treści

3. Metoda swobodnego stanowiska

Metoda ta stanowi niejako połączenie metody wcięcia wstecz z metodą biegunową. Stanowisko można obrać w dowolnym miejscu, następnie wykonywany jest pomiar do punktów osnowy. Mierzone mogą być odległości oraz kąty tak aby możliwe było wyznaczenie współrzędnych stanowiska z obliczenia wcięcia kątowego, liniowego bądź kątowo‑liniowego. Obliczenie dokonuje się w sposób automatyczny w oprogramowaniu tachimetru. W oparciu o obliczone współrzędne stanowiska oraz współrzędne punktów tyczonych zapisanych w pamięci instrumentu mamy możliwość tyczenia punktów metodą biegunową, gdyż kąty i odległości do tyczenia obliczane są w oprogramowaniu instrumentu.

RHkw1uuDQHohx

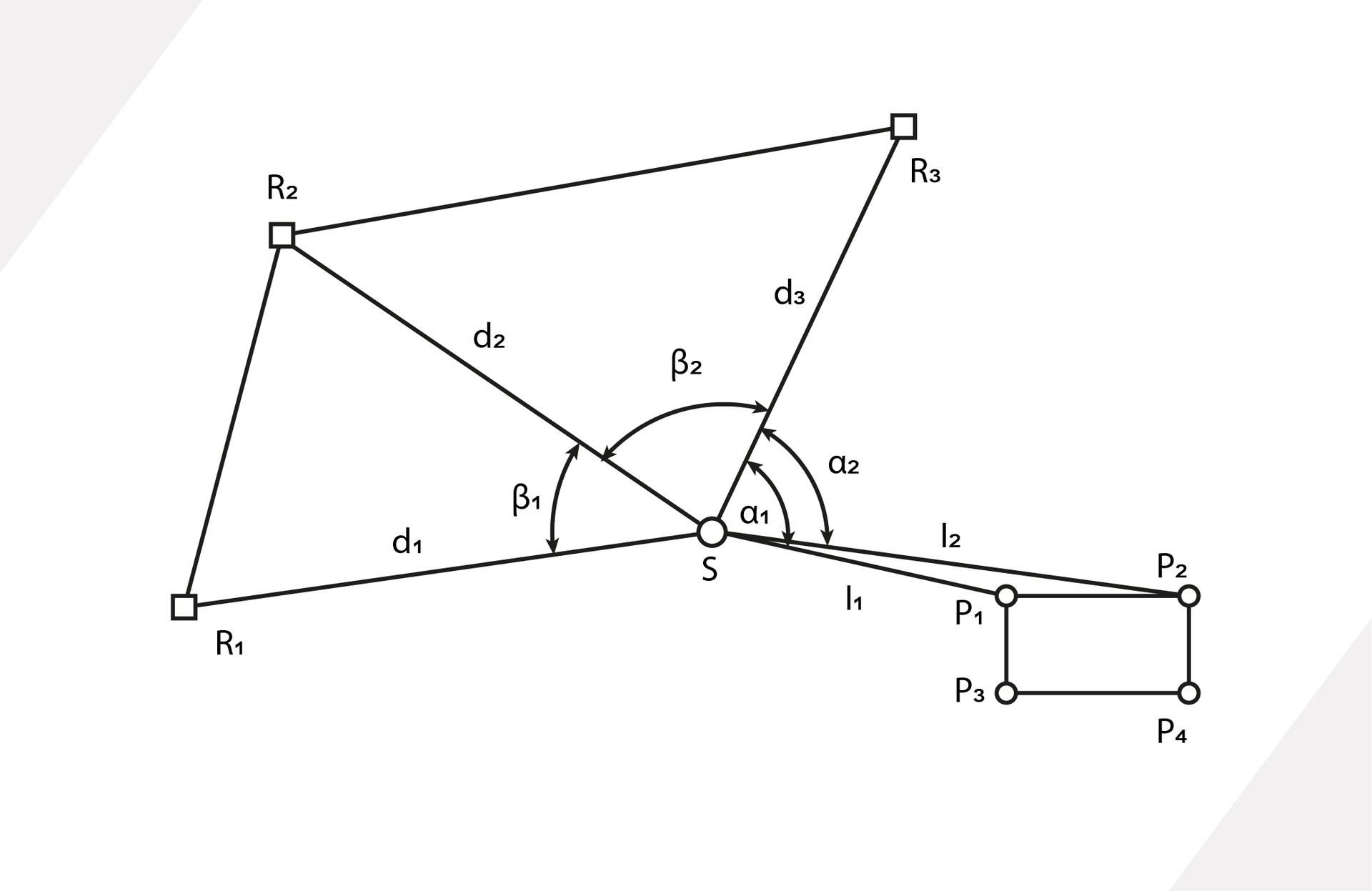
Grafika przedstawia tyczenie punktów metodą biegunową. Widoczne są dwa trójkąty równoboczne, połączone dłuższym bokiem ze sobą, który opisany jest jako d3 (trzy w indeksie dolnym), których wierzchołek skierowany jest w dół i oznaczony jako S. Po prawej stronie widoczny jest prostokąt w poziomie, od którego górnych narożników - oznaczonych jako P1 i P2 (1 i 2 w indeksie dolnym) - biegną dwie linie dochodzące do połączonego wierzchołka dwóch trójkątów, oznaczone jako I1 i I2 (1 i 2 w indeksie dolnym). Na narożnikach trójkątów widoczne są małe kwadraty, podpisane jako R1, R2 i R3 (1, 2 i 3 w indeksie dolnym). Na narożnikach prostokąta widoczne są małe kółka opisane jako P1, P2, P3, P4 (1‑2 w indeksie dolnym). Wewnątrz pierwszego trójkąta, przy wierzchołu widoczne jest zaznaczenie kąta z podpisem z literą beta 1 (1 w indeksie dolnym). Wewnątrz drugiego trójkąta, przy wierzchołu widoczne jest zaznaczenie kąta z podpisem z literą beta 2 (2 w indeksie dolnym). Pomiędzy wierzchołkiem trójkąta a liniami I1 i I2 (1 i 2 w indeksie dolnym) widoczne są zaznaczenia kąta podpisane jako a1 i a2 (1 i 2 w indeksie dolnym).

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 3.1 – tyczenie punktów metodą biegunową
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Zgodnie z powyższym rysunkiem, najpierw wybieramy lokalizację stanowiska pomiarowego S, następnie poprzez pomiar odległości dIndeks dolny 1, dIndeks dolny 2, dIndeks dolny 3 oraz kątów betaIndeks dolny 1 i betaIndeks dolny 2 do punktów osnowy realizacyjne wyznaczamy współrzędne stanowiska S. Dane do tyczenia punktów PIndeks dolny i obliczane są automatycznie w oprogramowaniu tachimetru, wybierając do tyczenia punkt PIndeks dolny 1 otrzymujemy informację o tym jaki kąt należy odłożyć alfaIndeks dolny 1 oraz jaką odległość należy odmierzyć lIndeks dolny 1.

Jest to metoda stosowana powszechnie w pomiarach realizacyjnych, bardzo dobrze sprawdza się w dynamicznym środowisku placu budowy. Niewątpliwym atutem jest możliwość dowolnego wyboru stanowiska. Jedynym ograniczeniem jest konieczność widoczności na punkty nawiązania, tak aby można było zrealizować wcięcie wstecz. Dane do tyczenia nie muszą być przygotowane przed przyjazdem na plac budowy, generowane są one automatycznie w oprogramowaniu instrumentu.

Powrót do spisu treściPowrót do spisu treści

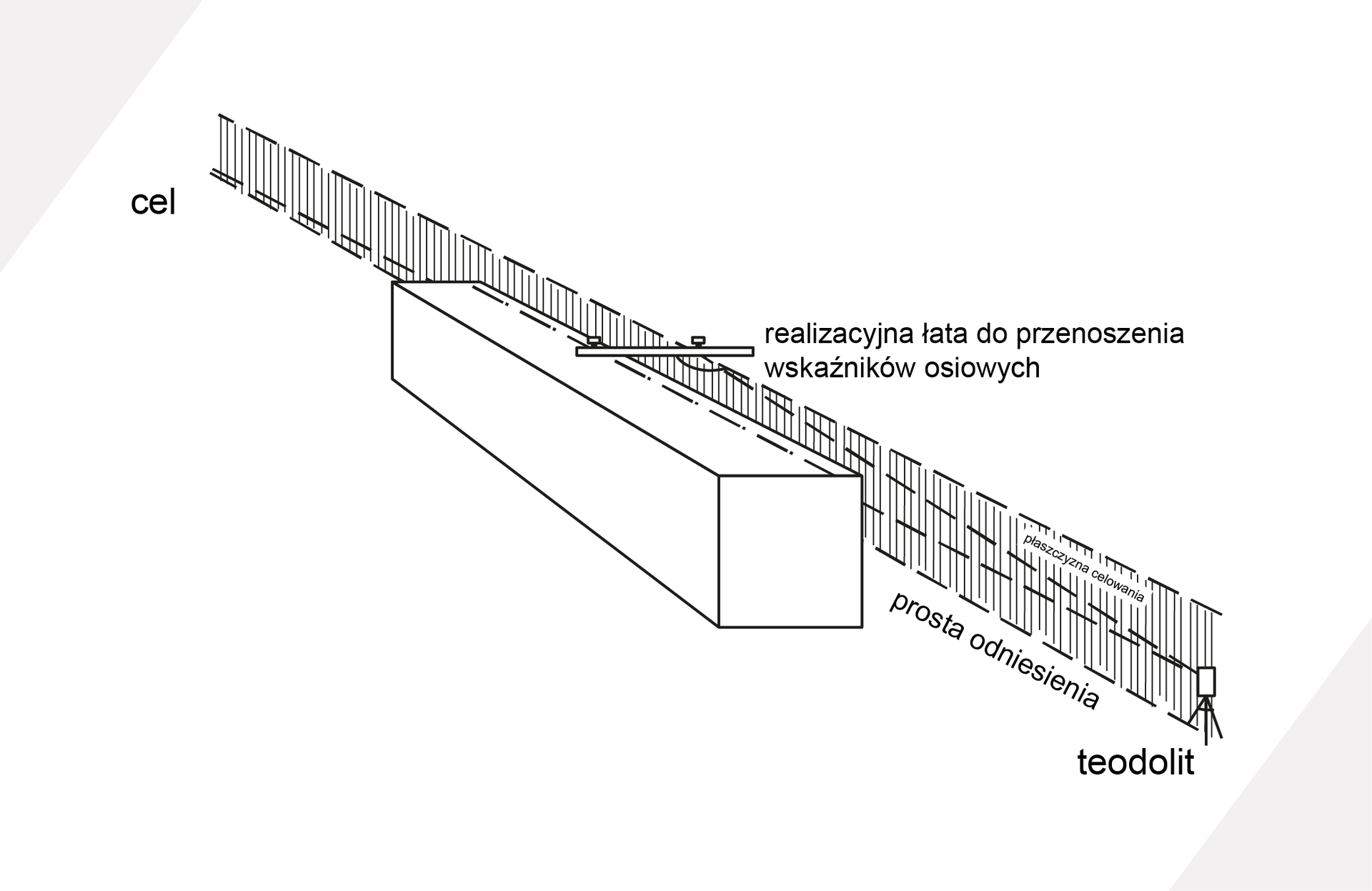
4. Metoda prostej odniesienia

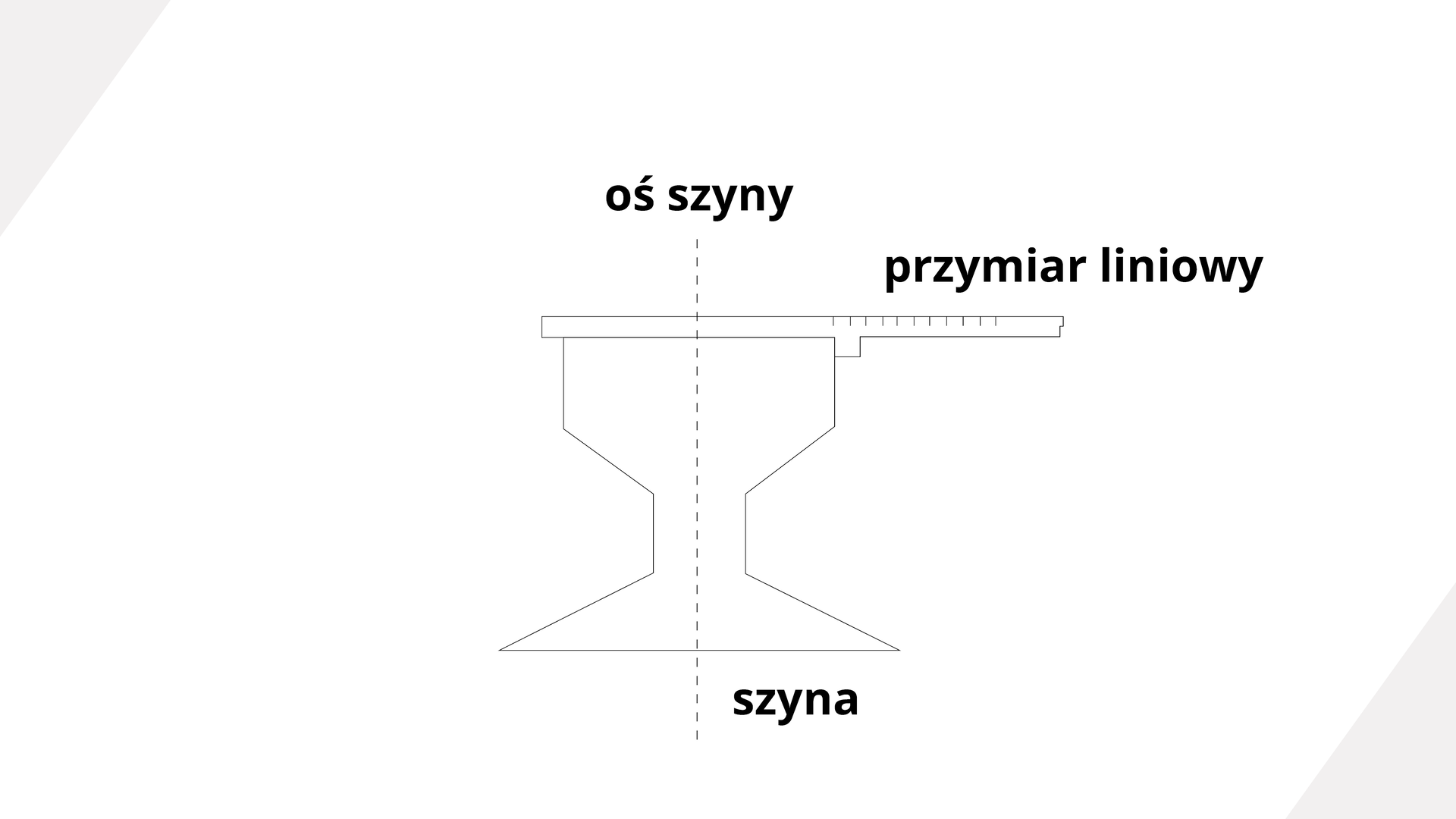
Metoda prostej odniesienia może być wykorzystywana zarówno w pomiarach realizacyjnych jak również podczas wykonywania pomiarów kontrolnych. W przypadku tyczenia obiektów, np. budynków mieszkalnych wielokondygnacyjnych metodę tę można wykorzystać podczas przenoszenia osi konstrukcyjnych budynku na kolejne poziomy. Polega ona na zrealizowaniu w terenie linii pomocniczych równoległych zarówno do osi poprzecznych jak i podłużnych odsuniętych około 1 m od zewnętrznych ścian tyczonego obiektu. Te dodatkowe linie markuje się w terenie z wykorzystaniem jednego lub dwóch znaków ziemnych. Następnie na jednym końcu linii ustawia się tarczę celowniczą na drugim zaś teodolity, celując na punkt końcowy wyznaczamy płaszczyznę odniesienia. Zmieniając tylko kąt nachylenia lunety celujemy na przymiar liniowy umieszczony na kolejnym poziomie, tak aby umożliwił on realizację stałej znanej odległości d od płaszczyzny odniesienia do wyznaczanej osi konstrukcyjnej.

Metodę tę można również z powodzeniem stosować w pomiarach kontrolnych suwnicy lub też punktów położonych na koronie zapory wzdłuż jej osi, w celu wyznaczenia odchyłek.

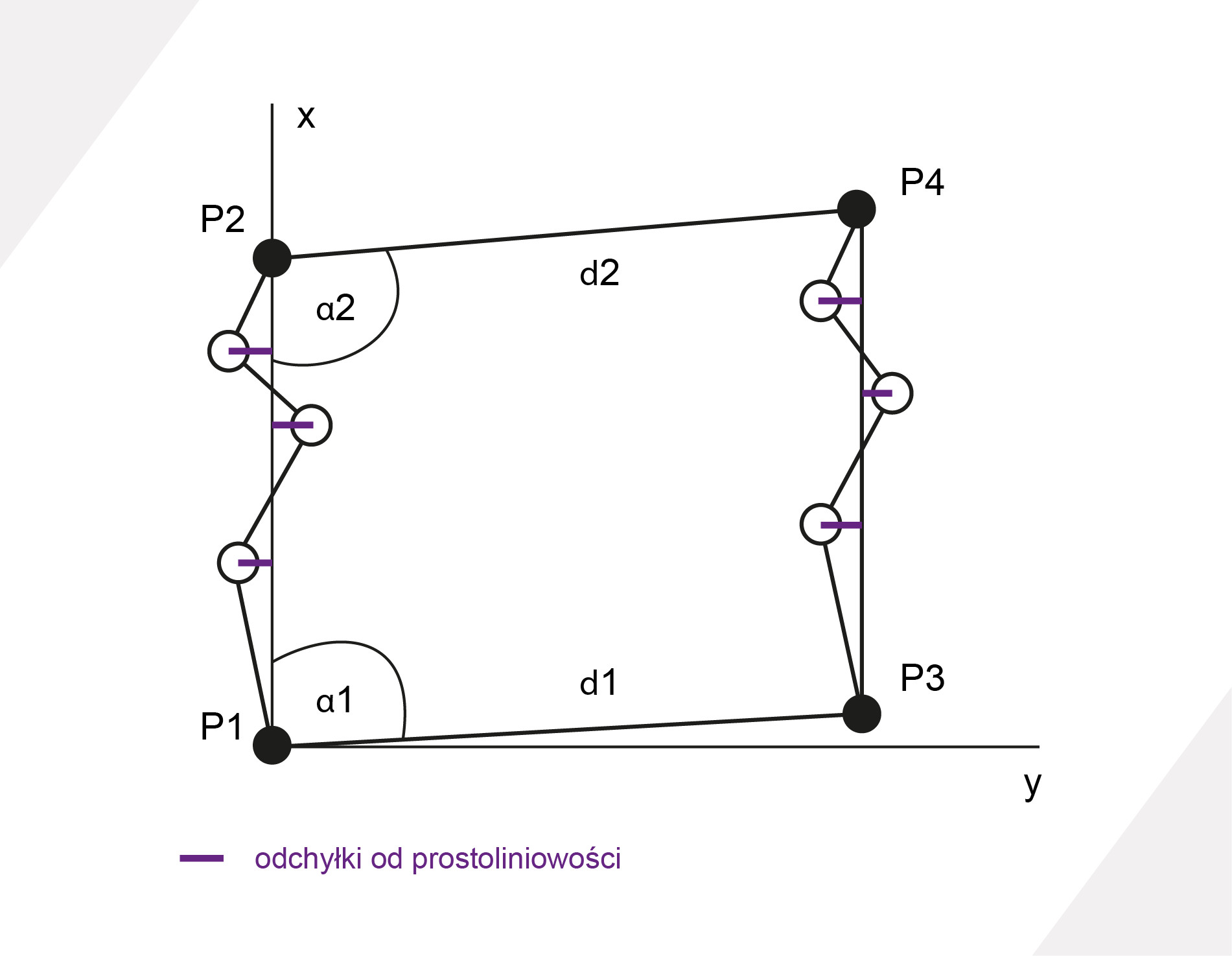
Prostą odniesienia można zrealizować z wykorzystaniem czworokąta. W tym przypadku zakładamy dwie proste odniesienia, po jednej dla każdej z szyn. W pierwszym i ostatnim przekroju oznaczamy punkty osiowe szyn, które tworzą wspomnianą prostą. W powstałym czworokącie P1,P2,P3,P4, (Rys. 2.1) dokonujemy pomiaru kątów alfa1, alfa2 oraz długości d1 oraz d2. Następnie dla każdej z szyn wykonujemy pomiar odchyleń poszczególnych punktów od prostej z wykorzystaniem przymiaru liniowego. (Rys. 2.2)

RcEsDwTKSUjiP

Ilustracja przedstawia układu pomiarowego w metodzie prostej odniesienia, proste P1‑P2 oraz P3‑P4, realizują osie szyn suwnicy, na każdym kolejnym punkcie mierzona jest odchyłka, wzajemnie powiązanie obu prostych uzyskujemy poprzez pomiar długości oraz kątów.

Na grafice widoczna jest oś współrzędnych xy. W oś wpisany został kwadrat, którego lewe narożniki dotykają osi x i oznaczone są jako P1 i P2, zaś prawe narożniki - oznaczone jako P3 i P4, są lekko podniesione ponad oś y. Przy lewych narożnikach widoczne jest zaznaczenie kątów opisanych jako a1 (dolny) i a2 (górny). Na narożnika widoczne są czarne kółka. Wzdłuż prawego i lewego boku widoczne są trzy okręgi połączone łamanymi liniami. Z okręgów wychodzą krótkie czarne linie. Bok dolny opisany jest jako d1, a górny jako d2.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 4.1 - ilustracja układu pomiarowego w metodzie prostej odniesienia, proste P1‑P2 oraz P3‑P4, realizują osie szyn suwnicy, na każdym kolejnym punkcie mierzona jest odchyłka, wzajemnie powiązanie obu prostych uzyskujemy poprzez pomiar długości oraz kątów
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

RQBHwUbCL1XJj

Grafika przedstawia pomiar odchylenia od prostej z wykorzystaniem przymiaru. Widoczny jest przekrój przedmiotu wyglądającego jak kielich na szerokiej stopce, podpisany: szyna. Pośrodku niego biegnie pionowa przerywana linia podpisana: oś szyny. Na górze widoczny jest wystający z prawej strony poziomy element podpisany: przymiar liniowy.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 4.2 – pomiar odchylenia od prostej z wykorzystaniem przymiaru
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

RzMIbphS89SNu

Grafika przedstawia przykład realizacji metody prostej odniesienia. Widoczny jest długi prostopadłościan w ujęciu z ukosa. Na środku górnej ściany prostopadłościanu widoczna jest pozioma linia podpisana: realizacyjna łata do przenoszenia wskaźników osiowych. Na froncie widoczny jest prostokąt na trzech nogach, podpisany: teodolit, z którego biegną dwie rozchodzące się przerywane linie. Po prawej stronie widoczne są dwie długie przerywane linie, widziane z ukosa, pomiędzy którymi biegną cienkie kreseczki. Dolna linia podpisana jest: prosta odniesienia. Na końcu lini dolnej napis: cel.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 4.3 – przykład realizacji metody prostej odniesienia
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

RedtDKnbaxSWl

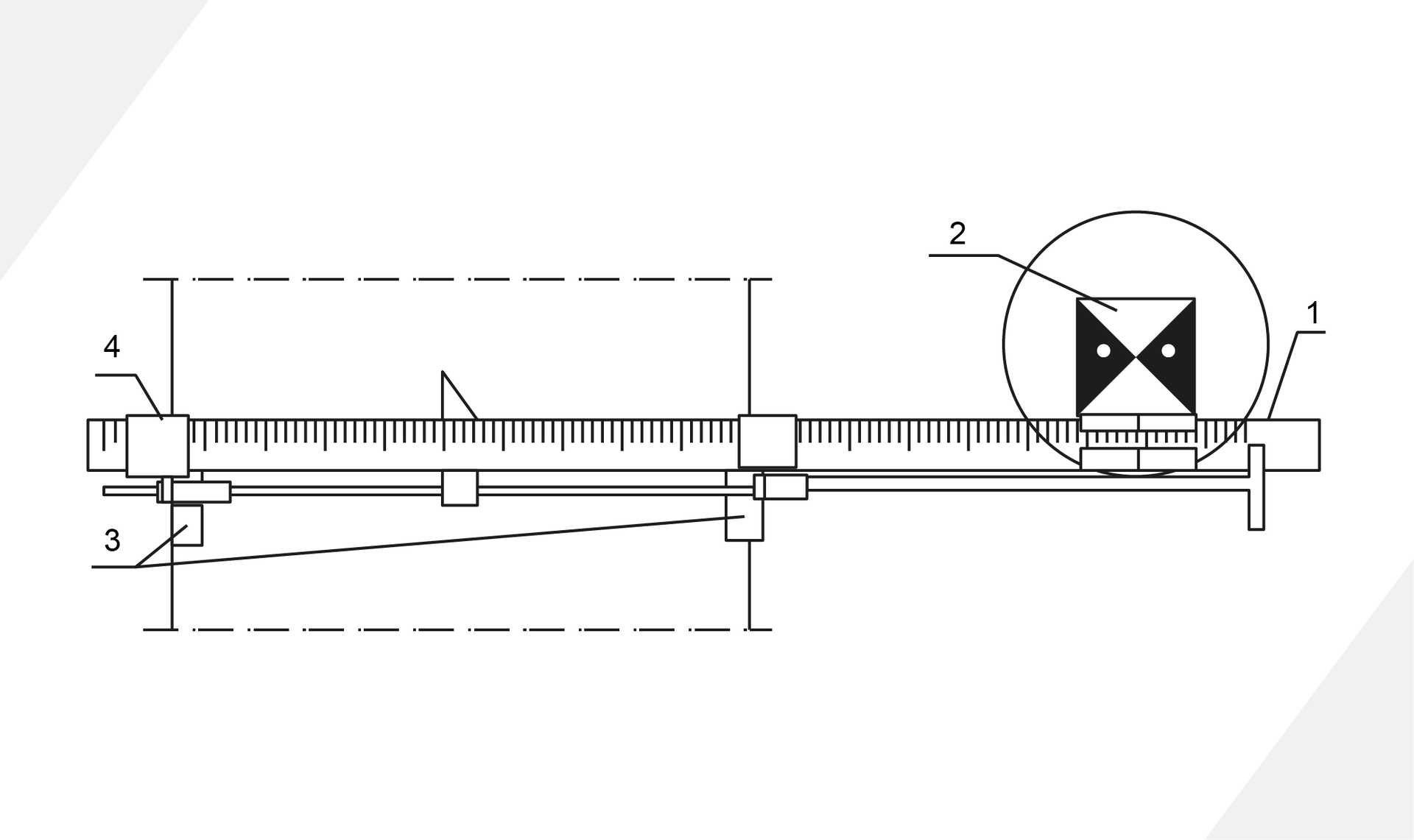
Grafika przedstawia przyrząd wykorzystywany w pomiarach prostej odniesienia. Od lewej widoczny jest długi prostokąt w poziomie, przy którego górnej krawędzi zaznaczone są drobne kreseczki, symbolizujące skalę. Element ten symbolizuje miarkę centymetrową. Na prawy końcu widoczny jest okrąg, w który wpisany jest prostokąt. Prostokąt podzielony jest przekątnymi na cztery trójkąty, z których prawy i lewy są czarne, z białymi kółeczkami tuż przy wierzchołach.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys. 4.4 – przyrząd wykorzystywany w pomiarach prostej odniesienia
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Powrót do spisu treściPowrót do spisu treści

5. Metoda rzutowania

Podobnie jak w przypadku metody prostej odniesienia, w budownictwie wielokondygnacyjnym metoda ta służy przenoszeniu osi konstrukcyjnych budynku na kolejne jego kondygnacje.

Z punktów osiowych utrwalonych na bokach ramy geodezyjnej rozwija się osnowę budowlano‑montażową. Punkty tej osnowy zastabilizowane w sposób trwały powinny się znajdować w płaszczyznach konstrukcyjnych.

RUYZ3TArAExQt

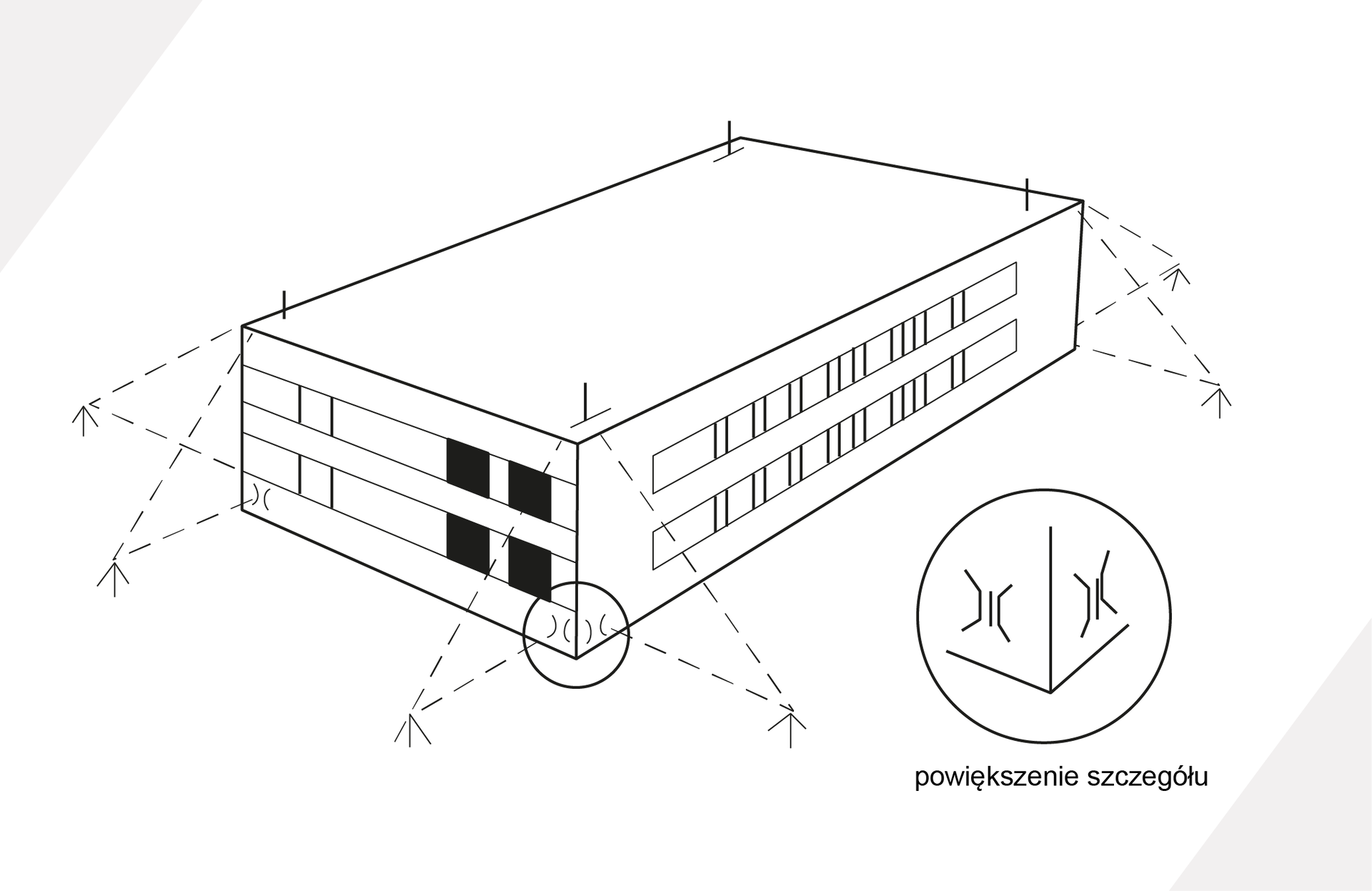
Grafika przedstawia przenoszenie osi metodą rzutowania. Grafika przedstawia prostopadłościan symbolizujący budynek, z dwoma rzędami białych kwadratów na dłuższym boku i dwoma rzędami białych i czarnych kwadratów na krótszym boku. Od górnych narożników prostopadłościanu biegną pod kątem przerywane linie, które łączą się z przerywanymi liniami biegnącymi od dolnych narożników prostopadłościanu, w ten sposób tworząc trójkąty. Na dolnym narożniku nałożony jest okrąg, którego powiększenie widoczne jest po prawej stronie.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys. 5.1 – przenoszenie osi metodą rzutowania
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

RgbFI9BhBs80H

Grafika przedstawia osnowę budowlano‑montażową do wykonania metody rzutowania. Na łososiowym tle widoczny jest pośrodku prostokąt. Tuż przy narożnikach prostokąta, na każdym z boków, widoczne są wychodzące krótkie przerywane linie zakończone czerwonymi kółkami, w które wpisane są numerki. Od lewego dolnego, zgodnie z ruchem wskazówek zegara: 1, 2, 0, 3, 4, 5, 6, 7. Od czerwonych kółek prowadzą krótkie przerywane linie zakończone żółtymi kółkami, w
które wpisane są numerki. Od lewego dolnego, zgodnie z ruchem wskazówek zegara: 1, 9, 8, 1, 1, 1, 1, 1. Czerwone kółka połączone są między sobą, tworząc prostokąt. Na narożnikach prostokąta widoczne są małe białe prostokąty z napisami, od lewego dolnego, zgodnie z ruchem wskazówek zegara: R4, R1, R2, R3.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys 5.2 – osnowa budowlano‑montażowa do wykonania metody rzutowania
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Instrumentem wykorzystywanym w tego typu pracach jest teodolit. Należy ustawić go nad punktem osnowy budowlano‑montażowej, następnie celując na wskaźnik ścienny zostaje wyznaczona płaszczyzna osi. Po wycelowaniu lunety na najwyższą kondygnację należy takie miejsce oznaczyć na krawędzi stropu. Po wyznaczeniu tej samej osi po drugiej stronie budynku można ją zrealizować fizycznie za pomocą struny stalowej.

Podczas wykorzystywania tej metody należy pamiętać o tym by odległość stanowiska od budynku była większa niż jego obecna wysokość, dzięki czemu możnas zmniejszyć potencjalny błąd wynikający z niepionowości osi teodolitu. Przy czym pamiętać trzeba o tym, że w przypadku ograniczonej przestrzeni wokół realizowanej inwestycji nie będzie można skorzystać z tej metody ze względu na brak możliwości zlokalizowania stanowisk instrumentu.

Powrót do spisu treściPowrót do spisu treści

6. Metoda przestrzennych wcięć kątowych

Jedną z metod która może być wykorzystana podczas obserwacji budowli powłokowej, np. chłodni kominowej jest metoda przestrzennych wcięć kątowych. Pomiar wykonywany jest do oznaczonych punktów na powierzchni budowli. Mogą być one oznaczone w sposób trwały z wykorzystaniem znaczków celowniczych lub sygnalizowane w trakcie wykonywania pomiaru z wykorzystaniem plamki lasera. W tym miejscu należy zaznaczyć, że trwała stabilizacja jest rzadko stosowana ze względu na koszty realizacji.

RdrbKm1tckVHS

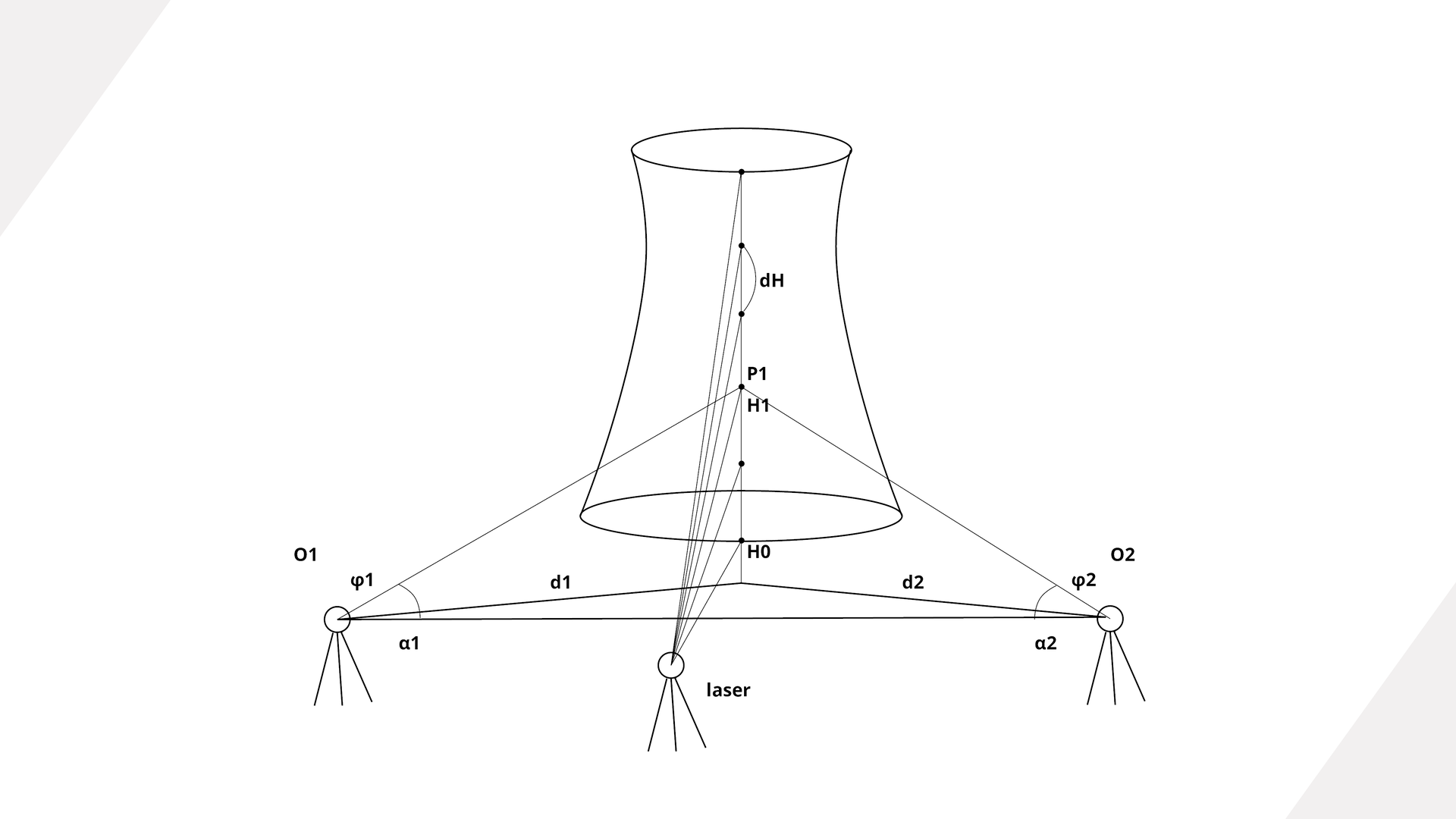
Grafika przedstawia metodę przestrzennych wcięć kątowych. Pośrodku widoczny jest cylindryczny zarys, zwężony w górnej części i rozszerzający się na dole, u podstawy. Od środka bryły biegną wychodzące na wprost i pod skosem linie, które zbiegają się w trzech punktach zaznaczonych jako okręgi, z których środkowy jest podpisany jako laser. Całość tworzy trójkąty.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys 6.1 – metoda przestrzennych wcięć kątowych
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Najpierw zostaje wyznaczona wysokość punktu H0, następnie przyjęta zostaje stała różnica wysokości dH między punktami sąsiednimi. Dla każdego z nich można ustalić kąt pionowy.

Obserwacje prowadzone są z punktów O1 oraz O2 gdzie wykonywany jest pomiar kąta poziomego alfa, kąta pionowego phi oraz odległości d.

Obecnie najbardziej przydatną metodą w obserwacji budowli powłokowych jest opisana w kolejnej części metoda biegunowa 3D

Powrót do spisu treściPowrót do spisu treści

7. Metoda biegunowa 3D

Metoda ta różni się od zwykłej metody biegunowej dodatkowo pomiarem kąta pionowego co przy znanej wysokości punktu osnowy będącego stanowiskiem obserwacyjnym pozwala również na wyznaczenie wysokości mierzonego punktu.

W przypadku pomiarów kontrolnych mierzone są punkty położone w płaszczyźnie pionowej przechodzącej przez stanowisko obserwacyjne. Pomiarowi podlegają kąt poziomy pomiędzy punktem nawiązania a punktem celu, odległość do celu, oraz kąt pionowy. Oczywiście aby można było zastosować tą metodę należy wykorzystać do pomiaru tachimetr bezlustrowy.

Dodatkowo metoda ta może zostać wykorzystana z powodzeniem w pomiarach kontrolnych dotyczących jezdni podsuwnicowych. Mamy wówczas możliwość wykonywania pomiaru instrumentem bezpośrednio z poziomu posadzki.

R6yDvjhsohCnD

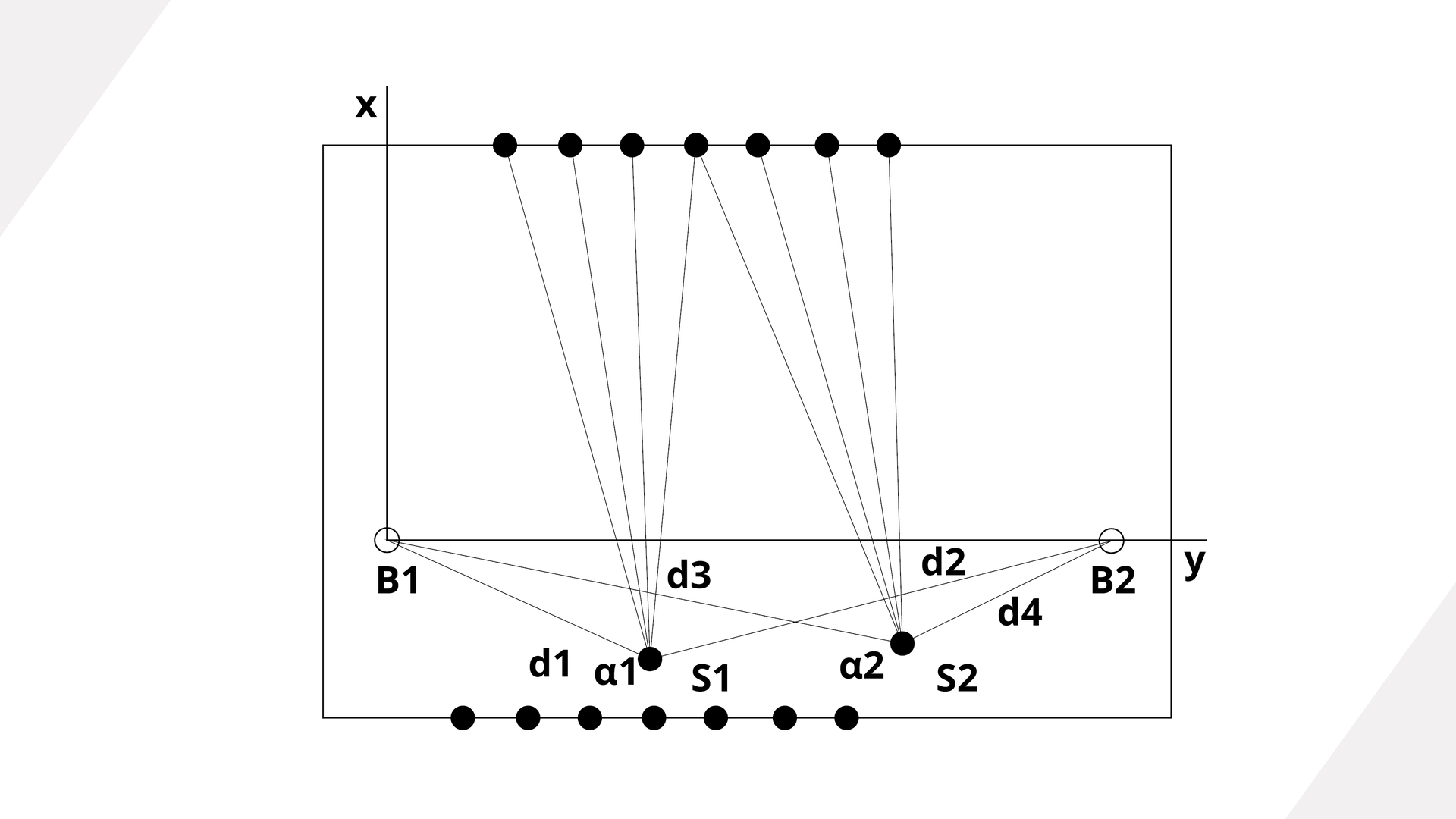
Grafika przedstawia metodę biegunową 3D. Widoczna jest oś xy, z punktem zero oznaczonym jako B1, na którą nałożony jest prostokąt wychodzący w lawo poza oś x i w dół poza oś y. Na górnym boku prostokąta osiem czarnych kółek, od których biegną w dół linie, które łączą się w dwóch czarnych kółkach znajdujących się poniżej osi y, podpisanych a1 i a2. Z punktu B1 i punktu B2, zaznaczonego na końcu osi y, biegną po dwie linie, które łączą się w punktach a1 i a2. Linie te podpisane są jako d1, d3 i d 2 i d4. Na dolnym boku prostokąta 7 czarnych kółek.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys 7.1 – metoda biegunowa 3D
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Na terenie hali/zakładu za pomocą pryzmatów oznaczana jest baza, umiejscowiona równolegle do osi głównej obiektu, tak aby oba punkty bazy (B1, B2) był widoczne z danego stanowiska obserwacyjnego (S1, S2). W celu wyznaczenia każdego punktu, tak jak wcześniej mierzony jest kąt poziomy, kąt pionowy oraz odległość do punktu.

Ponadto metoda ta jest wykorzystywana w pomiarach kontrolnych związanych z montażem dźwigarów w halach przemysłowych.

Powrót do spisu treściPowrót do spisu treści

8. Metoda trygonometryczna

Stanowi przykład tyczenia wykonywanego w dwóch etapach. W pierwszym etapie wyznacza się wstępnie punkt tyczony, w drugim wykonuje się pomiary kątów i odległości w seriach dla punktu tyczonego z dwóch znanych punktów osnowy. Otrzymane wyniki pomiarów poddaje się wyrównaniu w wyniku czego otrzymuje się poprawki trasowania. Wykorzystując obliczone poprawki zmienia się pierwotne położenie punktu na właściwe.

Metoda ta może być również wykorzystywana w pomiarach kontrolnych przy wyznaczaniu przemieszczeń poziomych, wówczas pomiary wykonywane są do punktów kontrolnych z punktów umiejscowionych poza obszarem oddziaływania.

Powrót do spisu treściPowrót do spisu treści

9. Metoda dwusiecznych kierunków stycznych

Jest to metoda wykonywania pomiarów kontrolnych wychyleń obiektów wieżowych. Polega na wyznaczeniu kątów zawartych pomiędzy kierunkiem do środka najniższego przekroju a kierunkami do środków na kolejnych poziomach obserwacyjnych. Kierunki te stanowią dwusieczne kątów pomiędzy celowymi które stanowią linie styczne do powierzchni trzonu na każdym przekroju obserwacyjnym.

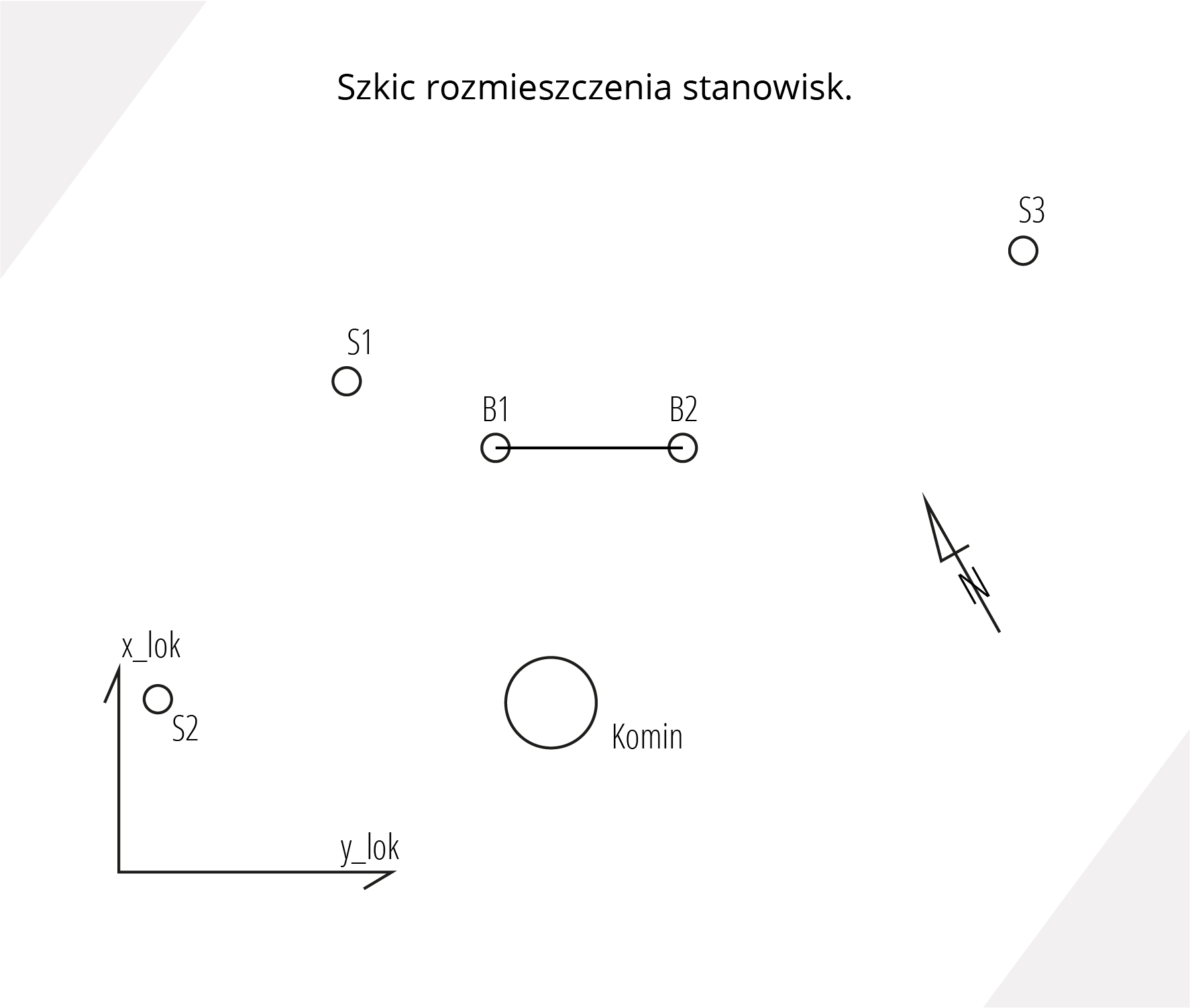
Przykład pomiarowy

Szkic rozmieszczenia stanowisk, ze względu na brak widoczności pomiędzy poszczególnymi stanowiskami obserwacyjnymi przywiązana jest do dwupunktowej bazy (B1, B2) ze współrzędnymi w układzie lokalnym

RS2Q29819fMpT

Grafika przedstawia szkic rozmieszczenia stanowisk. W lewym dolnym rogu widoczna jest oś xy, podpisana x_lok i y_lok. W górnej części osi x wpisany jest mały okrąg z napisem S2. Na prawo znajduje się okrąg z podpisem: Komin. Powyżej, pośrodku, widoczny odcinek, z punktami na końcach podpisanymi jako B1 i B2. Na lewo, lekko u góry od punktu B1, mały okrąg z podpisem S1. Na prawo, w górę od punktu B2, mały okrąg z podpisem S3. Po prawej stronie strzałka z oznaczeniem północy literą N.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka — Rys. 9.1 – szkic rozmieszczenia stanowisk
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Na podstawie obserwacji obliczono kierunki do osi komina jako dwusieczną kierunków stycznych

K_{i}^{j} = \frac{(L_{i}^{j} + P_{i}^{j})}{2}

gdzie:

i - i‑ty poziom
j - j‑te stanowisko
L, P – kierunki lewej i prawej stycznej

Następnie wyznaczono ochylenia kierunków od kierunku do poziomu 1 dla poszczególnych stanowisk

α_{i}^{j} = K_{i}^{j} - K_{1}^{j}

RjIClsq4BCsGH

Grafika przedstawia tabelę odchyleń kierunków do osi komina. U góry po lewej stronie nad tabelą napis: Kierunki do osi komina, zaś po lewej napis: Odchylenie kierunków w odniesieniu do poziomu 1. Poniżej w tabelki komórki z tytułami (od lewej) Poziom, St 01 [g], ST 02 [g], St 03 [g], Poziom, St 01 [cc], ST 02 [cc], St 03 [cc]. W dolnej części tabeli wpisane są poziomy oraz poszczególne wartości.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 9.2. – tabela odchyleń kierunków do osi komina
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Zestawiono równania obserwacyjne:

V_{α_{i}^{j}} = \frac{- sin (φ^{j})}{d^{j}} \times (ρ) \times (ω_{x i}) + \frac{cos (φ^{j})}{d^{j}} \times (ρ) \times (ω_{y i})

Wyznaczono wychylenia osi komina w poszczególnych poziomach wraz z analizą dokładności:

R1RE6fENjibij

Grafika przedstawia tabelę wychylenia osi komina w poszczególnych poziomach.
Widoczna jest tabela. U góry komórki z tytułami (od lewej) Poziom, Wysokość [m], wx [mm], mwx [mm], wy [mm], mwy [mm] - x i y w dolnym indeksie. W dolnej części tabeli wpisane są poziomy oraz poszczególne wartości.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys. 9.3 – wychylenia osi komina w poszczególnych poziomach
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Prezentacja graficzna wychylenia

Wykres wychyleń osi komina w płaszczyźnie XY

R1WOGQJUFVnHl

Wykres wychyleń osi komina w płaszczyźnie XZ

ROJq0gSPd9L1X

Wykres wychyleń osi komina w płaszczyźnie YZ

R13uYzKvOb3ye

Przykładowe dane obserwacyjne kierunków dla trzech stanowisk:

Cel	Seria I	Seria II	Różnica	Średnia	Średnia po redukcji
B1	0,0000	0,0045	-0,0045	0,0023	0,0000
1.1	13,7363	13,738	-0,0017	13,7372	13,7349
1.2	17,5589	17,5536	0,0053	17,5563	17,554
2.1	14,0507	14,0529	-0,0022	14,0518	14,0496
2.2	17,2336	17,2387	-0,0051	17,2361	17,2339
3.1	14,1774	14,1761	0,0013	14,1768	14,1745
3.2	17,0884	17,0906	-0,0022	17,0895	17,0873
4.1	14,3107	14,3128	-0,002	14,3117	14,3095
4.2	16,9236	16,9255	-0,0019	16,9245	16,9223
5.1	14,4376	14,4366	0,001	14,4371	14,4348
5.2	16,7865	16,7902	-0,0037	16,7883	16,7861

Cel	Seria I	Seria II	Różnica	Średnia	Średnia po redukcji
B1	0,0000	399,992	0,008	-0,0040	0,0000
1.1	30,5238	30,5225	0,0012	30,5231	30,5271
1.2	33,9656	33,9667	-0,0011	33,9662	33,9702
2.1	30,8229	30,8246	-0,0016	30,8237	30,8277
2.2	33,6568	33,6622	-0,0054	33,6595	33,6635
3.1	30,9324	30,9337	-0,0014	30,933	30,937
3.2	33,5606	33,5644	-0,0037	33,5625	33,5665
4.1	31,0706	31,0705	0,0001	31,0705	31,0745
4.2	33,4329	33,4416	-0,0087	33,4372	33,4412
5.1	31,1493	31,1481	0,0012	31,1487	31,1527
5.2	33,2755	33,2808	-0,0053	33,2781	33,2821

Cel	Seria I	Seria II	Różnica	Średnia	Średnia po redukcji
B2	-0,0011	0,0033	-0,0044	0,0011	0,0000
1.1	394,6084	394,6111	-0,0027	394,6097	394,6086
1.2	396,9453	396,9488	-0,0035	396,9470	396,9460
2.1	394,8074	394,8116	-0,0042	394,8095	394,8084
2.2	396,7559	396,7602	-0,0043	396,7581	396,7570
3.1	394,8773	394,8814	-0,0041	394,8793	394,8783
3.2	396,6742	396,6788	-0,0045	396,6765	396,6754
4.1	394,9625	394,9674	-0,0049	394,9649	394,9638
4.2	396,5662	396,5713	-0,0051	396,5688	396,5677
5.1	395,0578	395,0638	-0,0060	395,0608	395,0597
5.2	396,5103	396,5177	-0,0074	396,5140	396,5120

Na tej podstawie obliczono zestawienie kierunków dwusiecznych oraz odchyłek od poziomu bazowego

Kierunki do osi komina				Odchylenia kierunków w odniesieniu do poziomu bazowego
Poziom	S1 [g]	S2 [g]	S[3] g	Poziom	S1 [cc]	S2 [cc]	S3 [cc]
1	1,9096	1,7215	1,1687	1	0,0	0,0	0,0
2	1,9068	1,7185	1,1741	2	-27,4	-30,2	53,9
3	1,8960	1,7246	1,1682	3	-135,7	31,1	-4,6
4	1,8810	1,7308	1,1571	4	-285,7	92,4	-115,4
5	1,8755	1,6903	1,1777	5	-340,2	-312,6	90,0

Po rozwiązaniu układu równań normalnych z wykorzystaniem metody najmniejszych kwadratów uzyskano następujące wartości wychyleń na poszczególnych poziomach:

Poziom	Wysokość [m]	wx [mm]	mwx [mm]	wy [mm]	mwy [mm]
1	11,35	0,0	0,0	0,0	0,0
2	41,69	8,2	3,5	-4,9	5,4
3	58,7	2,7	9,6	21,3	14,5
4	79,7	-4,8	13,3	60,4	20,2
5	96,21	53,7	0,5	20,9	0,8

R1M8y7wDasrXp

Zdjęcie przedstawia przykład rozmieszczenia poziomów obserwacyjnych. Widoczne są trzy wysokie kominy pomalowane w poziome biało‑czerwone pasy. Na kominie pośrodku zaznaczono, po prawej stronie, poziome linie podpisane jako Poziom 2, Poziom 3, Poziom 4 i Poziom 5. Po lewej stronie w formie pionowych odcinku widoczne są podpisy, między poziomem 2 i 3 - 17,01 m; między poziomem 3 i 4 - 21,01 m; między poziomem 4 i 5 - 16,51m.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys 9.7 – Grafika ilustrująca przykład rozmieszczenia poziomów obserwacyjnych
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

Powrót do spisu treściPowrót do spisu treści

10. Przykład pomiarowy dotyczący wyznaczenia ugięcia i wyboczenia dźwigara

Szkic rozmieszczenia stanowisk

RmAtcaBdRCJW5

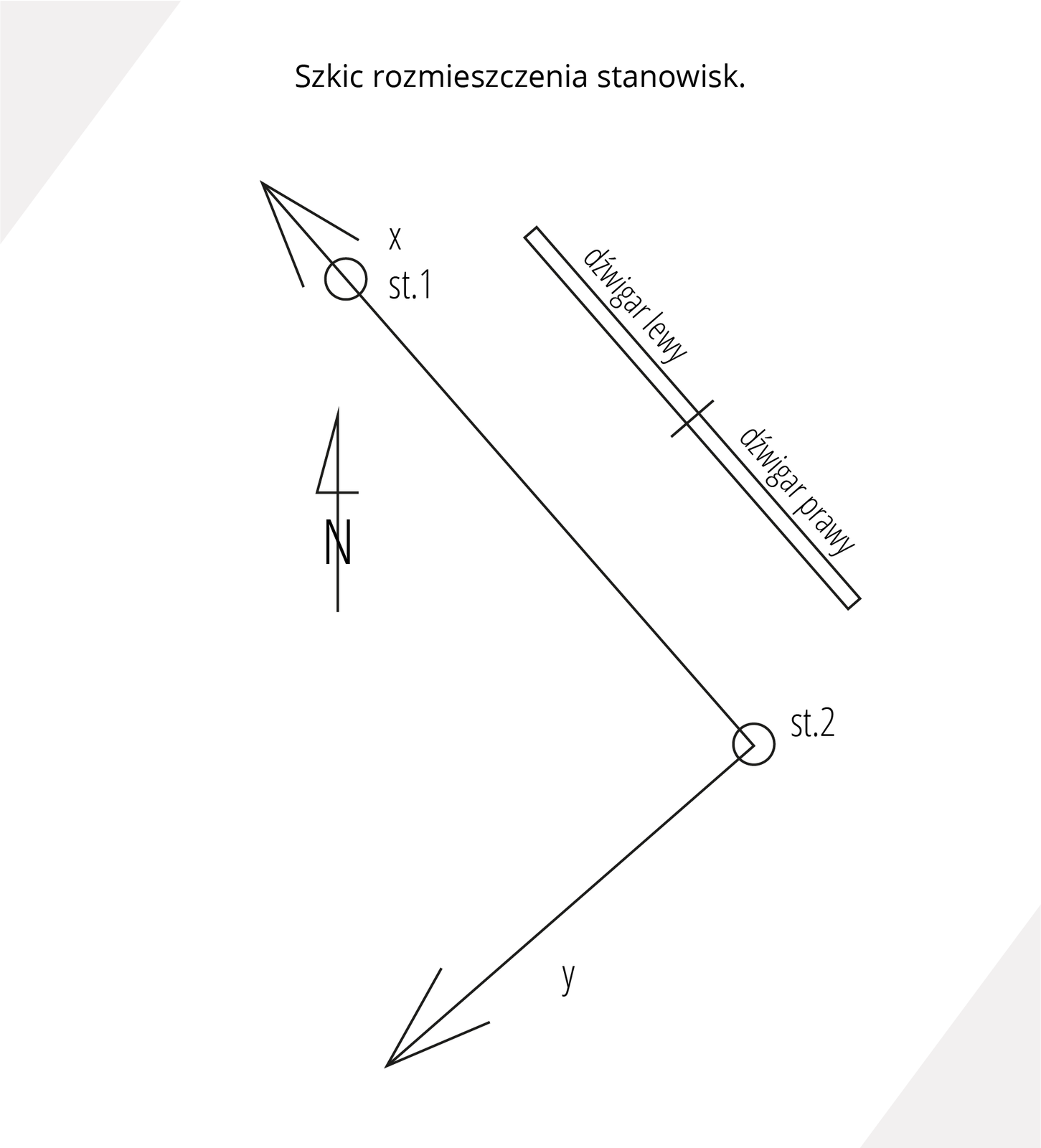
Współrzędne punktów przyjęto układzie lokalnym, dla stanowiska nr 2 (X=100.000m, Y=100.000m, H=100.000m,), na podstawie znanych wysokości instrumentów oraz pomiaru odległości obliczono współrzędne stanowiska nr 1 (X=214.393m, Y=100.000m, H=99.773m), oś X układu pokrywa się z bazą natomiast oś Y jest do niej prostopadła.

Współrzędne stanowisk
Stanowisko	X	Y	H
1	214.393	100.000	99.773
2	100.000	100.000	100.000

wysokości instrumentu

i1	1.652
i2	1.358
i2' (II seria)	1.402

kąty poziome

W oparciu o obliczone kąty poziome alfa i beta dla wszystkich punktów obliczono kąt gamma:

Punkt	alfa [g]	beta [g]	gamma [g]
P1	50.7783	61.2665	87.9552
P2	50.6926	61.3845	87.923
P3	50.6102	61.4934	87.8965
P4	50.3628	61.84	87.7973
P5	50.0409	62.2863	87.6729
P6	49.7208	62.7374	87.5419
P7	49.2129	63.4767	87.3105
P8	48.7135	64.222	87.0646
P9	48.4073	64.6929	86.8998
P10	48.1066	65.1493	86.7442
P11	47.3246	66.4056	86.2699
P12	46.4214	67.9435	85.6351
P13	45.5468	69.5259	84.9273
P14	44.7017	71.1386	84.1598
P15	43.8795	72.8068	83.3138
P16	43.087	74.5045	82.4086
P17	42.3168	76.2419	81.4413
P18	41.5701	78.0178	80.4121
P19	40.8439	79.8279	79.3282
P20	40.1413	81.6722	78.1866
P21	39.4626	83.544	76.9934
P22	38.9055	85.1416	75.9529
P23	38.699	85.7731	75.528
P24	38.4929	86.3849	75.1222
P25	38.1635	87.3847	74.4519
P26	37.841	88.3869	73.7722
P27	37.6407	89.0118	73.3476
P28	37.4435	89.6427	72.9139

Korzystając z twierdzenia sinusów obliczono odległości pomiędzy stanowiskami a mierzonym punktem:

a_{i} = \frac{d \times sin β}{sin γ}

b_{i} = \frac{d \times sin α}{sin γ}

gdzie: d – odległość pomiędzy stanowiskami

Następnie wyznaczono współrzędne X i Y wszystkich punktów:

X_{i} = X_{1} + a_{i} \times cos (200 - α)

Y_{i} = Y_{1} + a_{i} \times sin (200 - α)

lub

X_{i} = X_{2} + b_{i} \times cos β

Y_{i} = Y_{2} + b_{i} \times cos β

Odległości od stanowisk do mierzonych punktów wraz ze współrzędnymi

Punkt	b [m]	a [m]	XP_1 [m]	YP_1 [m]	XP_2 [m]	YP_2 [m]
P1	83.358	95.571	147.646	168.400	147.646	168.400
P2	83.257	95.703	147.461	168.404	147.461	168.404
P3	83.158	95.824	147.288	168.404	147.288	168.404
P4	82.865	96.212	146.749	168.419	146.749	168.419
P5	82.481	96.708	146.054	168.427	146.054	168.427
P6	82.099	97.206	145.357	168.433	145.357	168.433
P7	81.495	98.019	144.232	168.448	144.232	168.448
P8	80.901	98.831	143.111	168.458	143.111	168.458
P9	80.538	99.342	142.412	168.467	142.412	168.467
P10	80.179	99.832	141.733	168.462	141.733	168.462
P11	79.254	101.176	139.908	168.473	139.908	168.473
P12	78.198	102.800	137.733	168.492	137.733	168.492
P13	77.190	104.449	135.555	168.514	135.555	168.514
P14	76.232	106.105	133.388	168.531	133.388	168.531
P15	75.322	107.796	131.205	168.555	131.205	168.555
P16	74.470	109.495	129.033	168.578	129.033	168.578
P17	73.669	111.211	126.859	168.599	126.859	168.599
P18	72.925	112.945	124.683	168.621	124.683	168.621
P19	72.234	114.692	122.507	168.638	122.507	168.638
P20	71.606	116.455	120.331	168.659	120.331	168.659
P21	71.044	118.229	118.160	168.684	118.160	168.684
P22	70.616	119.732	116.332	168.701	116.332	168.701
P23	70.477	120.330	115.619	168.724	115.619	168.724
P24	70.331	120.901	114.927	168.729	114.927	168.729
P25	70.111	121.834	113.803	168.739	113.803	168.739
P26	69.912	122.767	112.683	168.752	112.683	168.752
P27	69.791	123.346	111.986	168.754	111.986	168.754
P28	69.681	123.931	111.287	168.761	111.287	168.761

Wyboczenia dla obu filarów wyznaczono w oparciu o wzór:

w_{i} = \pm Δ y_{i} \mp Δ x_{i} \times \frac{Δ y_{B A}}{Δ x_{B A}}

gdzie:

$Δ y_{i} = y_{i} - y_{A}$ – różnica współrzędnych kolejnych punktów względem początku dźwigara wzdłuż osi y

$Δ x_{i} = x_{i} - x_{A}$ - różnica współrzędnych kolejnych punktów względem początku dźwigara wzdłuż osi x

$Δ y_{B A} = y_{B} - y_{A}$ - różnica współrzędnych końca i początku dźwigara wzdłuż osi y

$Δ x_{B A} = x_{B} - x_{A}$ - różnica współrzędnych końca i początku dźwigara wzdłuż osi x

$B = L 28 l u b P 28$ - punkt końcowy dźwigara

$A = L 1 l u b P 1$ - punkt początkowy dźwigara

różnice wzdłuż osi x oraz osi y dla dźwigara

Punkt	deltaxi [m]	deltayi [m]
P1	0.000	0.000
P2	-0.185	0.004
P3	-0.358	0.004
P4	-0.897	0.019
P5	-1.592	0.027
P6	-2.289	0.033
P7	-3.414	0.048
P8	-4.535	0.058
P9	-5.234	0.067
P10	-5.913	0.062
P11	-7.738	0.073
P12	-9.913	0.092
P13	-12.091	0.114
P14	-14.258	0.131
P15	-16.441	0.155
P16	-18.613	0.178
P17	-20.787	0.199
P18	-22.963	0.221
P19	-25.139	0.238
P20	-27.315	0.259
P21	-29.486	0.284
P22	-31.314	0.301
P23	-32.027	0.324
P24	-32.719	0.329
P25	-33.843	0.339
P26	-34.963	0.352
P27	-35.660	0.354
P28	-36.359	0.361

różnice współrzędnych pomiędzy punktem końcowym a początkowym dźwigara

deltayIndeks dolny BA= 0.361 m
deltaxIndeks dolny BA = -36.359 m
zestawienie obliczonych wartości wyboczeń:

Punkt	P
Punkt	wi [mm]
1	0
2	-2
3	0
4	-10
5	-11
6	-10
7	-14
8	-13
9	-15
10	-3
11	4
12	6
13	6
14	11
15	8
16	7
17	7
18	7
19	12
20	12
21	9
22	10
23	-6
24	-4
25	-3
26	-5
27	0
28	0

kąty zenitalne V dla dźwigara

Punkt	phi1 [g]	phi2.1 [g]	phi2.2 [g]
P1	96.1373	95.5408	95.5762
P2	96.1407	95.5332	95.5685
P3	96.1449	95.5268	95.5617
P4	96.1567	95.5116	95.5436
P5	96.1708	95.4842	95.5171
P6	96.2474	95.5321	95.5700
P7	96.3766	95.6197	95.6527
P8	96.5110	95.7081	95.7497
P9	96.5889	95.7680	95.8070
P10	96.6693	95.8201	95.8584
P11	96.7104	95.7702	95.8073
P12	96.7610	95.7111	95.7493
P13	96.8081	95.6516	95.6880
P14	96.8568	95.5954	95.6349
P15	96.9055	95.5418	95.5795
P16	96.9517	95.4880	95.5269
P17	96.9996	95.4418	95.4786
P18	97.0459	95.3930	95.4356
P19	97.0919	95.3532	95.3922
P20	97.1375	95.3120	95.3537
P21	97.1812	95.2774	95.3179
P22	97.2160	95.2487	95.2900
P23	97.1802	95.1558	95.1958
P24	97.1440	95.0607	95.1007
P25	97.0825	94.9018	94.9403
P26	97.0252	94.7493	94.7886
P27	96.9928	94.6566	94.6970
P28	97.0098	94.6552	94.6963

Na podstawie uśrednionych kątów zenitalnych V oraz obliczonych wcześniej odległości od stanowisk do mierzonych punktów obliczono poszczególne przewyższenia:

W tym miejscu należy zaznaczyć, że w przypadku dźwigara dla stanowiska nr 2 uzyskano dla każdego z punktów dwa niezależne przewyższenia, ponieważ kąty zenitalne V pionowe nie mogły zostać uśrednione ze względu na różną wysokość stanowisk, w efekcie czego uśredniono dopiero obliczone wartości przewyższeń.

Wysokości poszczególnych punktów obliczono w oparciu o poniższe wzory:

h_{i}^{'} = H_{1} + i + Δ h_{i}

h_{i}^{″} = H_{2} + i^{'} + Δ h_{i}^{'}

h_{i}^{'} = \frac{h_{i}^{'} + h_{i}^{″}}{2}

gdzie:

i, i’ – wysokość instrumentu na poszczególnych stanowiskach

hIndeks dolny i – wysokości poszczególnych punktów

Odchyłki uzyskano w wyniku różnic wysokości, na ich podstawie wyznaczono błąd, który posłużył do obliczenia średnich błędów ugięcia każdego punktu.

m_{Δ h} = \frac{Σ f f}{n}

gdzie:

n – liczba mierzonych punktów

f – różnica wysokości

zestawienie obliczonych przewyższeń, wysokości, odchyłek oraz ostatecznej wysokości punktu dla dźwigara

Pkt	deltahi [m]	deltahi'2.1 [m]	deltahi'2.2 [m]	h'i [m]	h”i2.1 [m]	h”i2.2 [m]	h”i [m]	f [m]	hi [m]
P1	5.806	5.848	5.802	107.204	107.206	107.204	107.205	-0.001	107.205
P2	5.809	5.851	5.805	107.207	107.209	107.207	107.208	-0.001	107.208
P3	5.810	5.853	5.807	107.208	107.211	107.209	107.210	-0.002	107.209
P4	5.816	5.852	5.810	107.214	107.210	107.212	107.211	0.003	107.213
P5	5.824	5.861	5.818	107.222	107.219	107.220	107.219	0.003	107.221
P6	5.737	5.771	5.722	107.135	107.129	107.124	107.127	0.008	107.131
P7	5.585	5.616	5.574	106.983	106.974	106.976	106.975	0.008	106.979
P8	5.422	5.462	5.409	106.820	106.820	106.811	106.816	0.004	106.818
P9	5.328	5.362	5.312	106.727	106.720	106.714	106.717	0.010	106.722
P10	5.228	5.272	5.223	106.626	106.630	106.625	106.628	-0.001	106.627
P11	5.233	5.274	5.227	106.631	106.632	106.629	106.630	0.001	106.631
P12	5.235	5.276	5.229	106.633	106.634	106.631	106.633	0.001	106.633
P13	5.241	5.281	5.236	106.640	106.639	106.638	106.638	0.001	106.639
P14	5.243	5.283	5.235	106.641	106.641	106.637	106.639	0.003	106.640
P15	5.244	5.283	5.239	106.642	106.641	106.641	106.641	0.001	106.642
P16	5.247	5.287	5.241	106.645	106.645	106.643	106.644	0.001	106.645
P17	5.245	5.284	5.241	106.644	106.642	106.643	106.642	0.001	106.643
P18	5.245	5.287	5.238	106.643	106.645	106.640	106.642	0.001	106.643
P19	5.243	5.282	5.237	106.641	106.640	106.639	106.640	0.002	106.640
P20	5.240	5.283	5.235	106.638	106.641	106.637	106.639	-0.001	106.639
P21	5.238	5.280	5.234	106.637	106.638	106.636	106.637	0.000	106.637
P22	5.239	5.280	5.234	106.638	106.638	106.636	106.637	0.001	106.637
P23	5.333	5.373	5.329	106.732	106.731	106.731	106.731	0.001	106.731
P24	5.428	5.468	5.423	106.826	106.826	106.825	106.825	0.000	106.826
P25	5.587	5.627	5.584	106.986	106.985	106.986	106.985	0.000	106.986
P26	5.741	5.779	5.736	107.139	107.137	107.138	107.138	0.002	107.138
P27	5.831	5.872	5.827	107.229	107.230	107.229	107.229	0.000	107.229
P28	5.825	5.864	5.819	107.224	107.222	107.221	107.221	0.002	107.223

błąd średni ugięcia
dźwigar mIndeks dolny deltah Indeks dolny koniec= 3.3 [mm]
zestawienie różnic wysokości* $Δ u_{i} = h_{i} - h_{A}$ *różnica wysokości kolejnych punktów dźwigara

Punkt	P
Punkt	deltaui [m]
1	0.000
2	0.003
3	0.004
4	0.008
5	0.016
6	-0.074
7	-0.226
8	-0.387
9	-0.483
10	-0.578
11	-0.574
12	-0.572
13	-0.566
14	-0.565
15	-0.563
16	-0.560
17	-0.562
18	-0.562
19	-0.564
20	-0.566
21	-0.568
22	-0.567
23	-0.473
24	-0.379
25	-0.219
26	-0.066
27	0.025
28	0.018

różnica wysokości punktów początkowego i końcowego

dźwigar $Δ u_{B A} = 0.018 m$

Ugięcia dźwigarów obliczono ze wzoru:

u_{i} = \pm Δ u_{i} \mp Δ x_{i} \times \frac{Δ u_{B A}}{Δ x_{B A}}

gdzie:

$Δ u_{i} = h_{i} - h_{A}$ – różnica wysokości kolejnych punktów dźwigara

$Δ x_{i} = x_{i} - x_{A}$ - różnica współrzędnych kolejnych punktów względem początku dźwigara wzdłuż osi x

$Δ u_{B A} = h_{B} - h_{A}$ - różnica wysokości pomiędzy punktem końcowym dźwigara a początkowym

$Δ x_{B A} = x_{B} - x_{A}$ - różnica współrzędnych końca i początku dźwigara wzdłuż osi x

$B = L 28 l u b P 28$ - punkt końcowy dźwigara

$A = L 1 l u b P 1$ - punkt początkowy dźwigara

W oparciu o podany poniżej wzór wyznaczono błędy poszczególnych ugięć:

m_{u i} = \pm m_{Δ h} \mp \sqrt{1 + {(\frac{Δ u_{i}}{Δ x_{B A}})}^{2}}

Punkt	P	mui [mm]
Punkt	ui [mm]	mui [mm]
1	0	3.3
2	-3	3.3
3	-4	3.3
4	-7	3.4
5	-15	3.6
6	1	3.3
7	2	3.3
8	2	3.3
9	3	3.3
10	-1	3.3
11	-4	3.3
12	-5	3.3
13	-10	3.4
14	-10	3.4
15	-10	3.4
16	-12	3.5
17	-10	3.4
18	-8	3.4
19	-5	3.3
20	-2	3.3
21	1	3.3
22	1	3.3
23	-2	3.3
24	-2	3.3
25	-1	3.3
26	-1	3.3
27	-7	3.4
28	0	3.3

Ostatecznym etapem jest sporządzenie szkiców ugięć oraz wyboczeń dla dźwigara, skala dla obu osi powinna być zróżnicowana tak aby dobrze zaprezentować obliczone wartości, przykłady poniżej:

R3OZIgb5KzWnY

Grafika przedstawia wykres ugięć dźwigara.

Widoczna jest oś X w poziomie z jednostką [m], zamknięta po prawej i lewej stronie pionowymi liniami ze skalą od -20 do 15 na górze, co pięć. Przy prawej linii napis U oraz jednostka [mm]. Pomiędzy liniami ze skalą, przy każdej wartości, biegną poziome linie przerywane. Od pogrubione lini biegnącej na wartości zero, odchodzą w górę i w dół krótkie odcinki, zakończone małymi okręgami, podpisane od P1 do P.28 Z prawej, górnej strony legenda: Skala x - 1:200, Skala u - 2:1.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys 10.2 – wykres ugięć dźwigara
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

RzcwXZa7BRwOI

Grafika przedstawia wykres wyboczeń dźwigara.

Widoczna jest oś X w poziomie z jednostką [m], zamknięta po prawej i lewej stronie pionowymi liniami ze skalą od 20 do -15 na górze, co pięć. Przy prawej linii napis U oraz jednostka [mm]. Pomiędzy liniami ze skalą, przy każdej wartości, biegną poziome linie przerywane. Od pogrubione lini biegnącej na wartości zero, odchodzą w górę i w dół krótkie odcinki, zakończone małymi okręgami, podpisane od P1 do P.28 Z prawej, górnej strony legenda: Skala x - 1:200, Skala u - 2:1.

Opis prezentowanych na zdjęciu obrazów jest załączony w treści e‑booka. — Rys 10.3 – wykres wyboczeń dźwigara
Źródło: *Akademia Finansów i Biznesu Vistula*, licencja: CC BY 3.0.

DANE DO PRZELICZEŃ WŁASNYCH:

Wysokości instrumentu na poszczególnych stanowiskach, współrzędne stanowisk takie jak w powyższym przykładzie obliczeniowym

i1	1.652
i2	1.358

Kąty poziome

Punkt	alfa [g]	beta [g]
L1	74.4494	42.8018
L2	74.3090	42.8665
L3	74.1658	42.9337
L4	73.7490	43.1364
L5	73.2115	43.3944
L6	72.6736	43.6543
L7	71.8097	44.0895
L8	70.9601	44.5264
L9	70.4423	44.7996
L10	69.9280	45.0647
L11	68.5932	45.8053
L12	67.0454	46.7093
L13	65.5395	47.6456
L14	64.0767	48.6097
L15	62.6573	49.6043
L16	61.2751	50.6339
L17	59.9384	51.6922
L18	58.6364	52.7903
L19	57.3788	53.9148
L20	56.1581	55.0854
L21	54.9786	56.2869
L22	54.0219	57.3197
L23	53.6595	57.7455
L24	53.3005	58.1522
L25	52.7279	58.8198
L26	52.1723	59.4912
L27	51.8271	59.9171
L28	51.4898	60.3461

Kąty zenitalne V

Punkt	phi1 [g]	phi2 [g]
L1	94.9753	96.5694
L2	94.9794	96.5684
L3	94.9840	96.5623
L4	94.9990	96.5513
L5	95.0189	96.5340
L6	95.1103	96.5707
L7	95.2754	96.6378
L8	95.4419	96.7077
L9	95.5422	96.7490
L10	95.6231	96.7733
L11	95.6719	96.7323
L12	95.7282	96.6734
L13	95.7862	96.6241
L14	95.8474	96.5696
L15	95.9065	96.5133
L16	95.9682	96.4560
L17	96.0264	96.3962
L18	96.0887	96.3433
L19	96.1507	96.2873
L20	96.2150	96.2342
L21	96.2755	96.1781
L22	96.3263	96.1292
L23	96.2971	96.0601
L24	96.2472	95.9714
L25	96.1684	95.8295
L26	96.0926	95.6711
L27	96.0565	95.5874
L28	96.0758	95.5627

Źródła wykorzystane do przygotowania e‑booka:

Gocał J., Geodezja inżynieryjno‑przemysłowa, Wydawnictwo AGH 2010.
Jagielski A., Podstawy geodezji inżynieryjnej - standardy, pomiary realizacyjne, trasy, objętości, Geodpis 2012.

Powiązane materiały

Sekwencje filmowe – Pomiary realizacyjne i kontrolne obiektów budowlanychDlaiBPFqlSekwencje filmowe – Pomiary realizacyjne i kontrolne obiektów budowlanych
Wizualizacja – Charakterystyczne punkty obiektów inżynierskichD1CJHYqMJWizualizacja – Charakterystyczne punkty obiektów inżynierskich
Program ćwiczeniowy do projektowania – Lokalizacja punktów osnowy realizacyjnej i punktów kontrolnychDFd3UV508Program ćwiczeniowy do projektowania – Lokalizacja punktów osnowy realizacyjnej i punktów kontrolnych
Atlas interaktywny – Obiekty inżynierskieDAFImYNUXAtlas interaktywny – Obiekty inżynierskie

-Powrót do spisu treściPowrót do spisu treści