Fizyka sportu - zpe.gov.pl

R1O6wi2jAMrom

Sport to nie tylko rekreacja, mistrzostwa, gimnastyka, zabawa, fitness, zdrowy styl życia. W sporcie kryje się mnóstwo nauki. Poszczególne dyscypliny, treningi, ogólnie wszystko co dzieje się w sporcie, możemy analizować za pomocą mechaniki, ciągłych zmian energii, wykonywania pracy czy używania siły. Nauka, w tym fizyka, stanowi podstawę sportu.

Twoje cele

uporządkujesz wiedzę z zakresu mechaniki;
przeanalizujesz przemiany energii z jednej formy w drugą w sporcie;
zinterpretujesz zmiany energii potencjalnej i kinetycznej;
uporządkujesz wiedzę dotyczącą zasady zachowania energii;
przeanalizujesz, jakie znaczenia ma energia w sporcie.

Zasada zachowania energii

Zasada zachowania energiizasada zachowania energiiZasada zachowania energii jest jednym z podstawowych praw sformułowanych już w $XVIII$ wieku. Zakłada ona, że wartości energii mogą się zmieniać, ale całkowita energia pozostaje stała, jeśli żadne siły zewnętrze nie wykonują pracy nad rozpatrywanym układem. Energia może zmieniać swoją formę i przekształcać się, np. z kinetycznej w potencjalną. Energia kinetyczna związana jest z ruchem ciała i zależy od prędkości. Energia potencjalna może być energią potencjalną grawitacji – wynikającą z działania siły grawitacji lub energią potencjalną sprężystości – wynikającą z działania siły sprężystości.

Wyrażamy je następującymi wzorami:

energia kinetyczna:
$E_{K} = \frac{m \cdot v^{2}}{2}$ ,
gdzie:
$m$ – masa,
$v$ – prędkość;

energia potencjalna grawitacji:
$E_{P} = m \cdot g \cdot h$ ,
gdzie:
$m$ – masa,
$g$ – przyspieszenie ziemskie,
$h$ – wysokość;

energia potencjalna sprężystości:
$E_{P} = \frac{k \cdot x^{2}}{2}$ ,
gdzie:
$k$ – współczynnik sprężystości,
$x$ – odkształcenie ciała.

Przykład 1

Oblicz prędkość jaką uzyska zaraz po wystrzeleniu strzała o masie $50 g$ , jeśli łucznik podczas zawodów wystrzelił ją po naciągnięciu cięciwy łuku o $50 cm$ . Współczynnik sprężystości cięciwy wynosi $500 \frac{N}{m}$ . Załóż, że wystrzelenie strzały jest bezstratne, a łucznik strzela z pozycji leżącej (pomijamy energię potencjalną grawitacji).

Rozwiązanie:

W opisanej sytuacji, energia potencjalna sprężystości (wynikająca z naciągnięcia cięciwy łuku) jest przekazywana wystrzelonej strzale, która uzyskuje energię potencjalną. Z zasady zachowania energii wynika, że:

$E_{P} = E_{K}$ ,

a zatem:

$\frac{k \cdot x^{2}}{2} = \frac{m \cdot v^{2}}{2}$ .

Po przemnożeniu stronami przez $2$ otrzymujemy:

$k \cdot x^{2} = m \cdot v^{2}$ ,

przekształcamy wzór aby obliczyć prędkość:

$v^{2} = \frac{k \cdot x^{2}}{m}$ ,

a zatem:

$v = \sqrt{\frac{k \cdot x^{2}}{m}} = x \cdot \sqrt{\frac{k}{m}}$ .

Po wstawieniu wartości liczbowych:

$x = 50 cm = 0, 50 m$ ,

$k = 500 \frac{N}{m}$ ,

$m = 50 g = 0, 050 kg$ ,

obliczamy prędkość:

$v = 0, 50 m \cdot \sqrt{\frac{500 \frac{N}{m}}{0, 050 kg}} = 50 \frac{m}{s}$ .

Zasadę zachowania energii, jak i zmiany rodzajów energii, łatwo zauważyć w sporcie. We wszelkich sportach z użyciem piłek jak koszykówka, siatkówka, piłka nożna, ręczna, baseball, tenis, golf przenosimy energię za pomocą kija, rakiety lub rąk czy nóg gracza do piłki. Uzyskuje ona wtedy energię kinetyczną. Dla przykładu, w tenisie energia potencjalna z podniesionej ręki z rakietą zamieniana jest na energię kinetyczną rakiety. Rakieta, uderzając w piłkę, przekazuje jej energię kinetyczną, a wznosząca się piłka zyskuje dodatkowo energię potencjalną. Uderzenie takie nie jest idealne, część energii jest wytracana w momencie kontaktu rakiety z piłką. Piłka odkształca się delikatnie, by następnie wrócić do kształtu wyjściowego. Cała energia kinetyczna zatem nie jest przekazywana, pojawia się energia sprężystości. W sportach z użyciem kijów i piłek o dużej twardości jak golf, baseball czy bilard problem ten jest zmniejszany, energia przekazywana jest prawie całkowicie.

R1Pov6dgnDESh

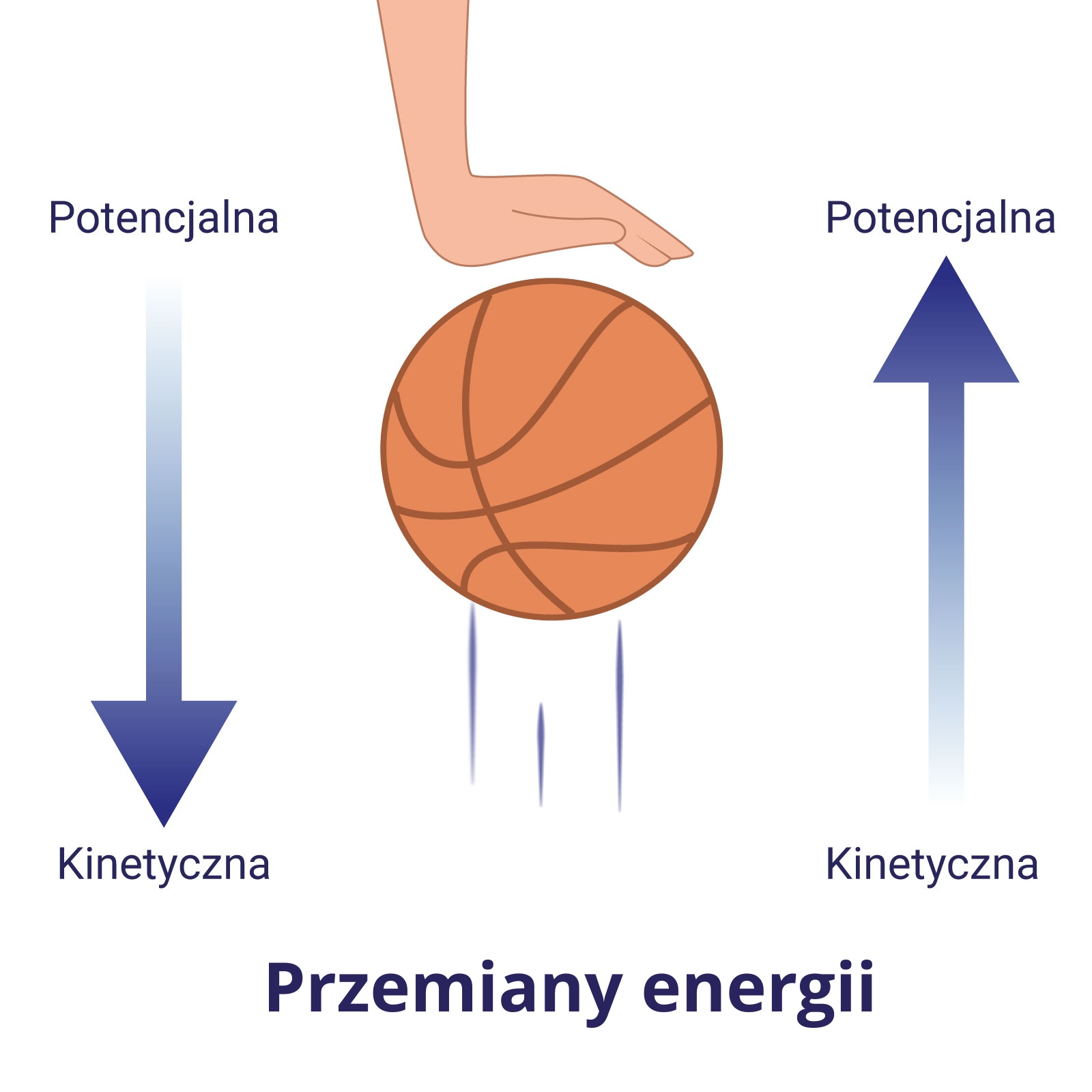
W centralnej części ilustracji piłka do koszykówki, oraz odbijająca ją ręka. Po lewej stronie strzałka skierowana pionowo w dół. Nad strzałką napis Potencjalna, pod strzałką napis Kinetyczna. Po prawej stronie strzałka skierowana pionowo w górę. Nad strzałką napis Potencjalna, pod strzałką napis Kinetyczna. Pod obrazkiem podpis: Przemiany energii. — Przemiany energii
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Sporty z użyciem piłki to nie jedyny przykład zmian energii. Podczas skoków narciarskich, zmiany energii zachodzą kilkakrotnie. Zawodnik na szczycie skoczni posiada tylko energię potencjalną grawitacji, w czasie zjazdu (a więc gdy zmniejsza się wysokość, na jakiej skoczek się znajduje) energia ta zamieniana jest w kinetyczną, która w momencie wyskoku ma maksymalną wartość. Następnie, podczas wznoszenia się skoczka, część energii kinetycznej zamieniana jest ponownie na potencjalną, by w momencie lądowania przeszła ona ponownie w kinetyczną i potencjalną sprężystości.

R1I4Wp6Ye5MuY

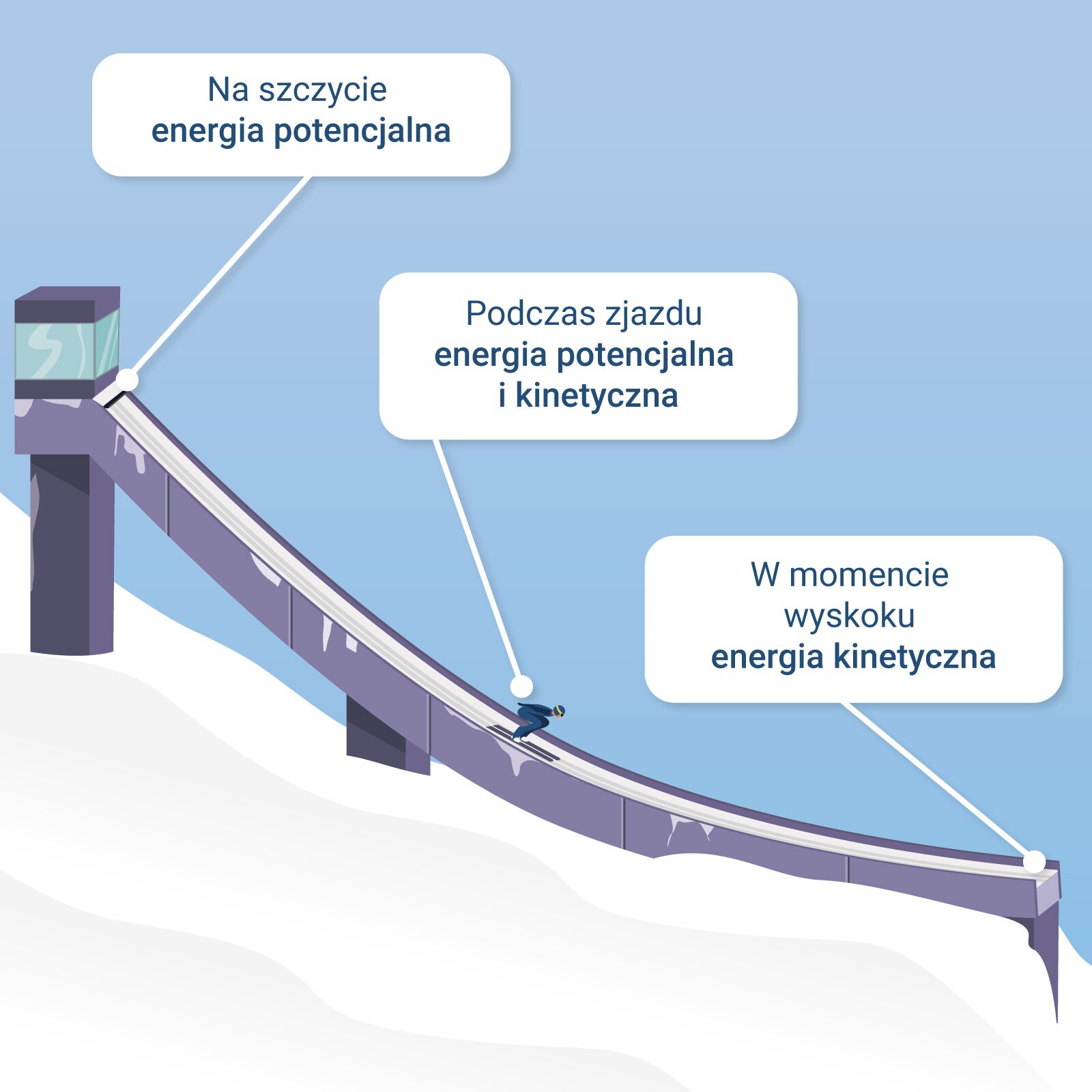
Skocznia narciarska, ze zjeżdżającym po niej skoczkiem. Na szczycie skoczni podpis: Na szczycie energia potencjalna. W centralnej części skoczni, w miejscu gdzie znajduje się skoczek, podpis: Podczas zjazdu energia potencjalna i kinetyczna. Na końcu skoczni podpis: W momencie wyskoku energia kinetyczna. — Zmiany energii
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Przykład 2

Skoczek narciarski uzyskał prędkość wyjścia z progu równą $111, 6 \frac{km}{h}$ . Jaka była wysokość najazdu skoczni? Opory pomiń.

Rozwiązanie:

Zakładamy, że w momencie wyjścia z progu skoczek posiada tylko energię kinetyczną, a przed startem na szczycie najazdu posiadał tylko energię potencjalną. Z zasady zachowania energii:

$E_{P} = E_{K}$ ,

a zatem:

$m \cdot g \cdot h = \frac{m \cdot v^{2}}{2}$ .

Po skróceniu mas otrzymujemy:

$g \cdot h = \frac{v^{2}}{2}$

i przekształcamy wzór w celu obliczania wysokości $h$ :

$h = \frac{v^{2}}{2 g}$ .

Podstawiamy odpowiednie wartości i obliczamy:

$v = 111, 6 \frac{km}{h} = 111, 6 \cdot \frac{1000 m}{3600 s} = 31 \frac{m}{s}$ ,

$g = 10 \frac{m}{s^{2}}$ ,

$h = \frac{{(31 \frac{m}{s})}^{2}}{2 \cdot 10 \frac{m}{s^{2}}} = 48 m$ .

W gimnastyce jest nie inaczej, przykład może stanowić skakanie na trampolinie. Podczas naskoku na trampolinę, zawodnik posiada energię potencjalną grawitacji, która zamieniana jest na energię kinetyczną. Energia ta zamieniana jest w chwili kontaktu na energię sprężystości trampoliny, która to energia następnie powoduje odbicie skoczka. Zyskuje on ponownie energię kinetyczną, a w momencie osiągnięcia maksymalnej wysokości energię potencjalną grawitacji. Cykl powtarza się przy kolejnych skokach.

RF3PF3dXLfpHw

Ilustracja przedstawia osobę skaczącą na trampolinie, w szczycie skoku. — Zmiana energii potencjalnej na energię kinetyczną podczas skoku na trampolinie
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zmiany energii ciężko dostrzec – jeśli przy uderzeniu nie zdeformuje się piłka, nie pęknie trampolina, to nie dają one efektów wizualnych. Efekty zmian energii możemy dostrzec w hollywoodzkich superprodukcjach, gdzie po lądowaniu superbohaterów kruszy się beton, a każde ich uderzenie niesie za sobą gigantyczną falę uderzeniową. Zastanówmy się jednak, czy to wszystko jest możliwe.

Przykład 3

Wyobraźmy sobie superbohatera posiadającego siłę $100$ mężczyzn, potrafiącego przeskoczyć wysoki budynek. Jaką prędkość początkową musi posiadać superczłowiek, i z jaką siłą odbić się od ziemi, aby przeskoczyć Pałac Kultury i Nauki w Warszawie? Załóżmy, że bezpiecznym skokiem, aby nie uszkodzić szczytu budynku, będzie wysokość $300 m$ , a czas odbicia od Ziemi trwa $0, 2$ sekundy. Masa bohatera wynosi $100 kg$ .

Rozwiązanie:

Z danych:

$E_{P} = m \cdot g \cdot h$ ,

$m = 100 kg$

$g = 10 \frac{m}{s^{2}}$ ,

$h = 300 m$ ,

możemy obliczyć, jaką energię potencjalną grawitacji będzie miał superbohater w szczycie skoku:

$E_{P} = 100 kg \cdot 10 \frac{m}{s^{2}} \cdot 300 m = 300000 J$ .

Z zasady zachowania energii wynika, że energia potencjalna w szczycie skoku musi być taka sama jak energia kinetyczna na początku skoku, możemy zatem obliczyć prędkość, jaką bohater uzyskał w wyniku wybicia:

$E_{K} = \frac{m \cdot v^{2}}{2}$ .

Po przekształceniach:

$v = \sqrt{\frac{2 E_{K}}{m}}$ ,

$v = \sqrt{\frac{2 \cdot 300000 J}{100 kg}} = 77, 5 \frac{m}{s}$ .

Prędkość ta została uzyskana w momencie wybicia, które trwało $0, 2$ sekundy, a zatem przyspieszenie wynosi:

$a = \frac{Δ v}{t}$ .

Zmiana prędkości następuje od zera, co daje:

$a = \frac{77, 5 \frac{m}{s}}{0, 2 s} = 387, 5 \frac{m}{s^{2}}$ .

Znając przyspieszenie, obliczamy siłę z jaką bohater działa na podłoże:

$F = m \cdot a$ ,

$F = 100 kg \cdot 387, 5 \frac{m}{s^{2}} = 3870 N$ .

R1ADdjctISVUP

Ilustracja przedstawia superbohatera skaczącego nad przepaścią. W tle widać miasto nocą. — Skoki superbohaterów w rzeczywistym świecie wiązałyby się z nieprzyjemnymi uszkodzeniami ciała
Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Człowiek ważący $100 kg$ wywiera około $1000 N$ siły na podłoże, podczas gdy w analizowanym przypadku jest to prawie $40$ razy więcej. Obliczona siła to czterokrotność siły, jaką wywiera ubijak do podłoża stosowany w profesjonalnych pracach budowlanych. Można przypuszczać, że superczłowiek, chcąc odbić się od podłoża, zapadłby się w nim na skutek zniszczeń, które by spowodował. Podobna sytuacja miałaby miejsce przy lądowaniu z takiej wysokości. Filmowi bohaterowie zawsze lądują w sposób efektowny, na pełne stopy lub klękając na kolano. Lądowanie takie spowodowałoby złamanie. Spadochroniarze, mimo że opadając na spadochronie nie rozwiną takiej dużej prędkości, to lądują z wykorzystaniem przewrotu przez ramię. Przetaczając się, zmniejszają siłę działającą tylko na jeden punkt swojego ciała.
Biorąc pod uwagę, dla odmiany, energię potrzebną do oddania takiego superskoku – $300000 J$ jest to energia pochodząca z mięśni bohatera, a zatem wpierw w tych mięśniach powinna zostać skumulowana. Odpowiada to około $70000$ kalorii, czyli około miesięcznemu zapotrzebowaniu dorosłego człowieka.
Wielu z komiksowych superbohaterów jest naukowcami, opracowują oni technologie, które pomagają im w walce z przestępczością. Jednym z takich pomysłów jest kostium absorbujący i kumulujący energię, którą bohater może następnie wykorzystać. Nagromadzenie dużej ilości energii daje śmiałkowi supersiłę. Pomysł ten wydaje się futurystyczny, lecz tak naprawdę nie jest daleki od realizacji. Już od $2009$ roku naukowcy z Politechniki Warszawskiej pracują nad inteligentnym materiałem, absorbującym energię uderzenia. Kumulowanie tej energii może wydawać się problematyczne, ale materiał taki może służyć do produkcji ochraniaczy sportowych, kamizelek kuloodpornych czy elementów konstrukcyjnych samochodów. Niektóre elementy z filmów superbohaterskich znajdują odzwierciedlenie w rzeczywistości.

Gra edukacyjna

Rozegraj grę i obroń miasto przed atakiem super‑złoczyńców.

R5PTjphmSxE4w

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Jesteś dowódcą drużyny superbohaterów, mających za zadanie zwalczenie paczki złoczyńców. Jeśli odpowiednio rozplanujesz atak, będziesz w stanie pokonać każdego z nich!

Polecenie 1

R1UYy9XO5Ndjz

Połącz w pary. Rozważnie wybierz, którego bohatera wyślesz do walki ze złoczyńcą. Piłkarz
energia kopnięcia piłki

350 J

Możliwe odpowiedzi: 1. Złowrogi Młot
rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

bez prędkości początkowej, 2. Człowiek Kula
masa

m = 75 kg

prędkość

v = 10 \frac{m}{s}

, 3. Gumowy Rabuś
współczynnik sprężystości

k = 300 \frac{N}{m}

maksymalne odkształcenie

x = 1, 5 m

, 4. nie wysyłam do walki, 5. Mistrzyni Procy, posiada dwie proce
dla gumy każdej z proc:
współczynnik sprężystości

k = 6000 \frac{N}{m}

maksymalne odkształcenie

x = 0, 1 m

Baseballista
energia uderzenia piłki

3800 J

Możliwe odpowiedzi: 1. Złowrogi Młot
rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

bez prędkości początkowej, 2. Człowiek Kula
masa

m = 75 kg

prędkość

v = 10 \frac{m}{s}

, 3. Gumowy Rabuś
współczynnik sprężystości

k = 300 \frac{N}{m}

maksymalne odkształcenie

x = 1, 5 m

, 4. nie wysyłam do walki, 5. Mistrzyni Procy, posiada dwie proce
dla gumy każdej z proc:
współczynnik sprężystości

k = 6000 \frac{N}{m}

maksymalne odkształcenie

x = 0, 1 m

Siatkarz
energia serwowanej piłki

80 J

Możliwe odpowiedzi: 1. Złowrogi Młot
rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

bez prędkości początkowej, 2. Człowiek Kula
masa

m = 75 kg

prędkość

v = 10 \frac{m}{s}

, 3. Gumowy Rabuś
współczynnik sprężystości

k = 300 \frac{N}{m}

maksymalne odkształcenie

x = 1, 5 m

, 4. nie wysyłam do walki, 5. Mistrzyni Procy, posiada dwie proce
dla gumy każdej z proc:
współczynnik sprężystości

k = 6000 \frac{N}{m}

maksymalne odkształcenie

x = 0, 1 m

Łucznik
energia strzały

3300 J

Możliwe odpowiedzi: 1. Złowrogi Młot
rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

bez prędkości początkowej, 2. Człowiek Kula
masa

m = 75 kg

prędkość

v = 10 \frac{m}{s}

, 3. Gumowy Rabuś
współczynnik sprężystości

k = 300 \frac{N}{m}

maksymalne odkształcenie

x = 1, 5 m

, 4. nie wysyłam do walki, 5. Mistrzyni Procy, posiada dwie proce
dla gumy każdej z proc:
współczynnik sprężystości

k = 6000 \frac{N}{m}

maksymalne odkształcenie

x = 0, 1 m

Skoczek w dal
energia skoku

50 J

Możliwe odpowiedzi: 1. Złowrogi Młot
rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

bez prędkości początkowej, 2. Człowiek Kula
masa

m = 75 kg

prędkość

v = 10 \frac{m}{s}

, 3. Gumowy Rabuś
współczynnik sprężystości

k = 300 \frac{N}{m}

maksymalne odkształcenie

x = 1, 5 m

, 4. nie wysyłam do walki, 5. Mistrzyni Procy, posiada dwie proce
dla gumy każdej z proc:
współczynnik sprężystości

k = 6000 \frac{N}{m}

maksymalne odkształcenie

x = 0, 1 m

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 2

R11vQ9ki3eAcx

Przyporządkuj do odpowiednich grup. Złoczyńcy postanowili się przegrupować, teraz walczą w parach! Wyślij do walki odpowiednich bohaterów. Do każdej pary złoczyńców możesz wysłać tylko jednego bohatera! Gumowy Rabuś (współczynnik sprężystości

k = 300 \frac{N}{m}

, maksymalne odkształcenie

x = 1, 5 m

)
Złowrogi Młot (rzuca młotem o masie

m = 10 kg

z wysokości

h = 30 m

, bez prędkości początkowej) Możliwe odpowiedzi: 1. Skoczek w dal (energia skoku

50 J

), 2. Siatkarz (energia serwowanej piłki

80 J

), 3. Łucznik (energia strzały

3300 J

), 4. Baseballista (energia uderzenia piłki

3800 J

), 5. Golfista (energia uderzenia piłeczki

4000 J

), 6. Piłkarz (energia kopnięcia piłki

350 J

), 7. Hokeista (energia uderzenia krążka

230 J

) Człowiek Kula (masa

m = 75 kg

, prędkość

v = 10 \frac{m}{s}

)
Mistrzyni Procy, posiada dwie proce (współczynnik sprężystości

k = 6000 \frac{N}{m}

, maksymalne odkształcenie

x = 0, 1 m

) Możliwe odpowiedzi: 1. Skoczek w dal (energia skoku

50 J

), 2. Siatkarz (energia serwowanej piłki

80 J

), 3. Łucznik (energia strzały

3300 J

), 4. Baseballista (energia uderzenia piłki

3800 J

), 5. Golfista (energia uderzenia piłeczki

4000 J

), 6. Piłkarz (energia kopnięcia piłki

350 J

), 7. Hokeista (energia uderzenia krążka

230 J

) Nie wysyłam Możliwe odpowiedzi: 1. Skoczek w dal (energia skoku

50 J

), 2. Siatkarz (energia serwowanej piłki

80 J

), 3. Łucznik (energia strzały

3300 J

), 4. Baseballista (energia uderzenia piłki

3800 J

), 5. Golfista (energia uderzenia piłeczki

4000 J

), 6. Piłkarz (energia kopnięcia piłki

350 J

), 7. Hokeista (energia uderzenia krążka

230 J

)

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 3

RZvQaFPCluwxy

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 1

Energia strzały łucznika wynosi $3300 J$ . Jaki jest współczynnik sprężystości cięciwy, jeśli łucznik naciąga ją na $40 cm$ ?

RerbhbzKqIeoa

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Współczynnik sprężystości $k$ wyznaczamy, przekształcając odpowiednio wzór na energię potencjąlną sprężystości:

$E_{P} = \frac{k \cdot x^{2}}{2}$ ,

$k = \frac{2 E_{p}}{x^{2}}$ .

A zatem:

$k={\large\frac{2\cdot3300\,\mathrm{J}}{\left(0,4\,\mathrm{m}\right)^2}}={\large\frac{6600\,\mathrm{J}}{0,16\,\mathrm{m}^2}}=41250\,\mathrm{\large\frac{N}{m}}$ .

Współczynnik sprężystości wynosi $41250 \frac{N}{m}$ .

Polecenie 2

Oblicz energie na kartach złoczyńców, wiedząc że:

Gumowy Rabuś – współczynnik sprężystości $k=300\,\mathrm{\large\frac{N}{m}}$ , maksymalne odkształcenie $x=1,5\,\mathrm{m}$ ;

Człowiek Kula – masa $m=75\,\mathrm{kg}$ , prędkość $v=10\,\mathrm{\large\frac{m}{s}}$ ;

Mistrzyni Procy – posiada dwie proce, dla gumy każdej z proc współczynnik sprężystości $k=6000\,\mathrm{\large\frac{N}{m}}$ , maksymalne odkształcenie $x=0,1\,\mathrm{m}$ ;

Złowrogi Młot – rzuca młotem o masie $m = 10\,\mathrm{kg}$ z wysokości $h=30\,\mathrm{m}$ , bez prędkości początkowej;

przyspieszenie grawitacyjne $g=10\,\mathrm{\large\frac{m}{s^2}}$ .

R1Z1DTfw6rPl4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Potrzebne wzory:

$E={\large\frac{mv^2}{2}}$ ,

$E={\large\frac{kx^2}{2}}$ ,

$E=mgh$ .

Gumowy Rabuś: $E={\large\frac{300\,\mathrm{\frac{N}{m}}\cdot\left(1,5\,\mathrm{m}\right)^2}{2}}=337,5\,\mathrm{J}$ ;

Człowiek Kula: $E={\large\frac{75\,\mathrm{kg}\cdot\left(10\,\mathrm{\frac{m}{s}}\right)^2}{2}}=3750\,\mathrm{J}$ ;

Mistrzyni Procy: $E=2\cdot{\large\frac{6000\,\mathrm{\frac{N}{m}}\cdot\left(0,1\,\mathrm{m}\right)^2}{2}}=60\,\mathrm{J}$ ;

Złowrogi Młot: $E=10\,\mathrm{kg}\cdot10\,\mathrm{\large\frac{m}{s^2}}\cdot30\,\mathrm{m}=3000\,\mathrm{J}$ .

Energie na kartach złoczyńców wynoszą:

energia Gumowego Rabusia – $337,5\,\mathrm{J}$ ;

energia Człowieka Kuli – $3750\,\mathrm{J}$ ;

energia Mistrzyni Procy – $60\,\mathrm{J}$ ;

energia Złowrogiego Młota – $3000\,\mathrm{J}$ .

Polecenie 3

Wymyśl swojego superbohatera! Podaj współczynniki postaci oraz oblicz energię z nich wynikającą.

R1XKticJrChGn

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Przydatne wzory:

$E={\large\frac{mv^2}{2}}$ ,

$E={\large\frac{kx^2}{2}}$ ,

$E=mgh$ .

Moim superbohaterem jest pewien rowerzysta (ważący $90\,\mathrm{kg}$ ), który jeździ na rozwerze szosowym (ważącym $10\,\mathrm{kg}$ ), z prędkością $75\,\mathrm{\large\frac{km}{h}}$ . Energia podczas jazdy z tą prędkością po prostej drodze wynosi:

$E={\large\frac{100\,\mathrm{kg}\cdot\left(75\,\mathrm{\frac{km}{h}}\right)^2}{2}}=20\,\mathrm{kJ}$ .

Sprawdź się

RzNKxoiIQBCqU

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

RrurkEC4XRPSQ

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 2

Dopasuj zadania prawdziwe i fałszywe do odpowiednich ramek.

Rl9MoTGrn9caw

Ilustracja przedstawia lecącego superbohatera w czerwonej pelerynie. W tle miasto nocą. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Rcl5VGWKKjy2S

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 3

Dziewczynka o masie równej $35 kg$ stoi na wysokości $120 m$ . Oblicz jej energię. Rozwiązanie i odpowiedź zapisz w polu poniżej.

RaevyrO7MYdct

Na zdjęciu dziewczynka w pomarańczowej pelerynie, spoglądająca ku morzu, usianemu skałami. Obok Niej trzy ramki z napisami: masa trzydzieści pięć kilogramów, wysokość sto dwadzieścia metrów, energia znak zapytania. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

RRM0IR30bxA4q

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

$E_{K} = 0$ – ponieważ dziewczynka nie porusza się.

$E = E_{P} = m \cdot g \cdot h = 35 kg \cdot 10 \frac{m}{s^{2}} \cdot 120 = 42000 J$

Energia dziewczynki wynosi $42000 J$ .

RsLHFTAH9GjsR

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1Q2ExpfbmDxf

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Rovy3zisvJV30

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 6

Superbohater Shadowman o masie $90 kg$ , znajdujący się $5 m$ nad ziemią, wystrzelił linę w punkt znajdujący się dokładnie nad złoczyńcą Śmieszkiem. Wykonując swobodny swing na linie, zamierza znokautować bandziora. Z jaką energią uderzy w Śmieszka?

RH2OFrlZQcIh3

Ilustracja przedstawia superbohatera lecącego na linie w stronę superzłoczyńcy. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R11pTxdVnp70V

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Będąc na wysokości $5 m$ nad ziemią, bohater posiada energię potencjalną grawitacji.

$E_{P} = 90 kg \cdot 10 \frac{m}{s^{2}} \cdot 5 m = 4500 J$

Jest to energia, która zostanie zamieniona na kinetyczną w trakcie swingu i wykorzystana do obezwładnienia bandyty.

Energia, z jaką Shadowman uderzy w Śmieszka, będzie wynosiła $4500 J$ .

RrALjgVS7lfex

Ćwiczenie 7

Ułóż od najmniejszej do największej energii bohatera. Elementy do uszeregowania: 1. Biały Orzeł (podczas lotu): masa bohatera

85 kg

, prędkość lotu

20 \frac{m}{s}

, wysokość na jakiej się znajduje

120 m

, 2. Shadowman (stojący na gzymsie budynku): masa bohatera

90 kg

, wysokość na jakiej się znajduje

87 m

, 3. Supersprinter (podczas biegu): masa bohatera

70 kg

, prędkość

30 \frac{m}{s}

, 4. Mega-Łucznik (naciągający łuk): współczynnik sprężystości

800 \frac{N}{m}

, naciągnięcie

50 cm

, 5. Super-Syrena (wyskakująca z wody, w szczycie lotu): masa bohatera

55 kg

, wysokość skoku

2 m

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 8

Jakie energie mają superbohaterowie z poprzedniego ćwiczenia? Przyjmij wartość przyspieszenia ziemskiego wynoszącą $10\,\mathrm{\large\frac{m}{s^2}}$ . Rozwiązanie i odpowiedź zapisz w polu poniżej.

Rqp8uJU9OMXpz

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Przydatne wzory:

$E={\large\frac{mv^2}{2}}$ ,

$E={\large\frac{kx^2}{2}}$ ,

$E=mgh$ .

Supersprinter (podczas biegu) - masa bohatera $70 kg$ , prędkość bohatera $30 \frac{m}{s}$ :

$E={\large\frac{70\,\mathrm{kg}\cdot\left(30\,\mathrm{\large\frac{m}{s}}\right)^2}{2}}=31500\,\mathrm{J}$ .

Biały Orzeł (podczas lotu) - masa bohatera $85 kg$ , prędkość $20 \frac{m}{s}$ , wysokość na jakiej się znajduje $120 m$ :

$E=85\,\mathrm{kg}\cdot10\,\mathrm{\large\frac{m}{s^2}}\cdot120\,\mathrm{m}+{\large\frac{85\,\mathrm{kg}\cdot\left(20\,\mathrm{\large\frac{m}{s}}\right)^2}{2}}=119000\,\mathrm{J}$ .

Mega‑Łucznik (naciągający łuk) - współczynnik sprężystości łuku $800 \frac{N}{m}$ , naciągnięcie $50 cm$ :

$E={\large\frac{800\,\mathrm{\frac{N}{m}}\cdot\left(40\,\mathrm{cm}\right)^2}{2}}=100\,\mathrm{J}$ .

Super‑Syrena (wyskakująca z wody, w szczycie lotu) - masa $55 kg$ , wysokość skoku $2 m$ : $E=55\,\mathrm{kg}\cdot10\,\mathrm{\large\frac{m}{s^2}}\cdot2\,\mathrm{m}=1100\,\mathrm{J}$ .

Shadowman (stojący na gzymsie budynku) - masa bohatera $90 kg$ , wysokość na jakiej się znajduje $87 m$ :

$E=90\,\mathrm{kg}\cdot10\,\mathrm{\large\frac{m}{s^2}}\cdot87\,\mathrm{m}=78300\,\mathrm{J}$ .

Energie bohaterów wynoszą:

Supersprintera – $31500 J$ ,

Białego Orła – $119000 J$ ,

Mega–Łucznika – $100 J$ ,

Super–Syreny – $1100 J$ ,

Shadowmana – $78300 J$ .

R1BpVIL5n5MHU

Ćwiczenie 9

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Słownik

zasada zachowania energii

zasada, zgodnie z którą w układzie izolowanym, a więc w układzie do którego nie jest dostarczana energia ani materia, ilość energii się nie zmienia; w takim układzie dozwolona jest zmiana jednej formy energii w inną.

Bibliografia

Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., 2017, Świat fizyki, Warszawa, WSiP

bg‑gray2

Notatki

R1NTRnbZpUEz2

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.