Gdyby Księżyc był wielkości piksela. Skala rozmiarów i odległości w Układzie Słonecznym
Układ Słoneczny jest ogromny, a jego rozmiar jest trudny do wyobrażenia przy użyciu standardowych jednostek, którymi posługujemy się na co dzień. Odległość od Ziemi do Księżyca to prawie , a do Słońca to prawie milionów kilometrów . Najdalsza planeta układu, Neptun, jest odległa od Słońca o prawie miliarda kilometrów . To tak naprawdę nic, w porównaniu z odległościami do gwiazd – jest to rząd wielkości –, a najdalsza galaktyka, odkryta przez teleskop Hubble'a, oddalona jest o około . W astronomii używa się najczęściej specjalnych jednostek opisujących te odległości. Inną metodą jest przedstawienie tego za pomocą odpowiedniej skali.
zintepretujesz astronomiczne jednostki odległości;
zastosujesz odpowiednie jednostki do opisu odległości w Układzie Słonecznym;
przeliczysz jednostki stosowane w astronomii;
przedstawisz odległości i modele za pomocą skali.
Ze względu na to, że odległości kosmiczne są duże, to zwykle nie podaje się ich w metrach czy kilometrach. W astronomii posługujemy się specjalnymi jednostkami. Są to między innymi lata świetlne. Jeden rok świetlny (, ang. light year)rok świetlny (, ang. light year) określa odległość jaką światło przebywa w ciągu roku. Prędkość światła jest wielkością stałą, więc dosyć łatwo obliczyć, jaką odległość nazywamy rokiem świetlnym.
Oblicz ile i ile to jeden rok świetlny.
Rozwiązanie:
Do obliczeń użyjemy standardowego wzoru na prędkość
,
gdzie oznacza drogę, a czas.
Wzór przekształcamy tak, by obliczyć drogę:
,
jako prędkość podstawiamy prędkość światła:
,
a jako czas rok wyrażony w sekundach (rok to w przybliżeniu dni, dzień to godziny, godzina to minut, a minuta to sekund):
.
Obliczamy drogę jaką przebywa światło w ciągu roku:
,
co w przeliczeniu na kilometry daje .
Wartość tabelaryczna roku świetlnego to . Jednostka ta ułatwia opisywanie odległości w astronomii. Dla przykładu podając odległość od Słońca do Neptuna, zamiast napisać możemy zastosować .
Inne jednostki, stosowane do określania kosmicznych odległości, to jednostka astronomiczna (, ang. (astronomical unit)jednostka astronomiczna (, ang. (astronomical unit) lub parsek (, ang. parsec)parsek (, ang. parsec). Jednostka astronomiczna określa odległość Ziemi od Słońca, wynosi dokładnie , w przybliżeniu milionów kilometrów. Dzięki temu łatwiej określić odległości planet od Słońca.
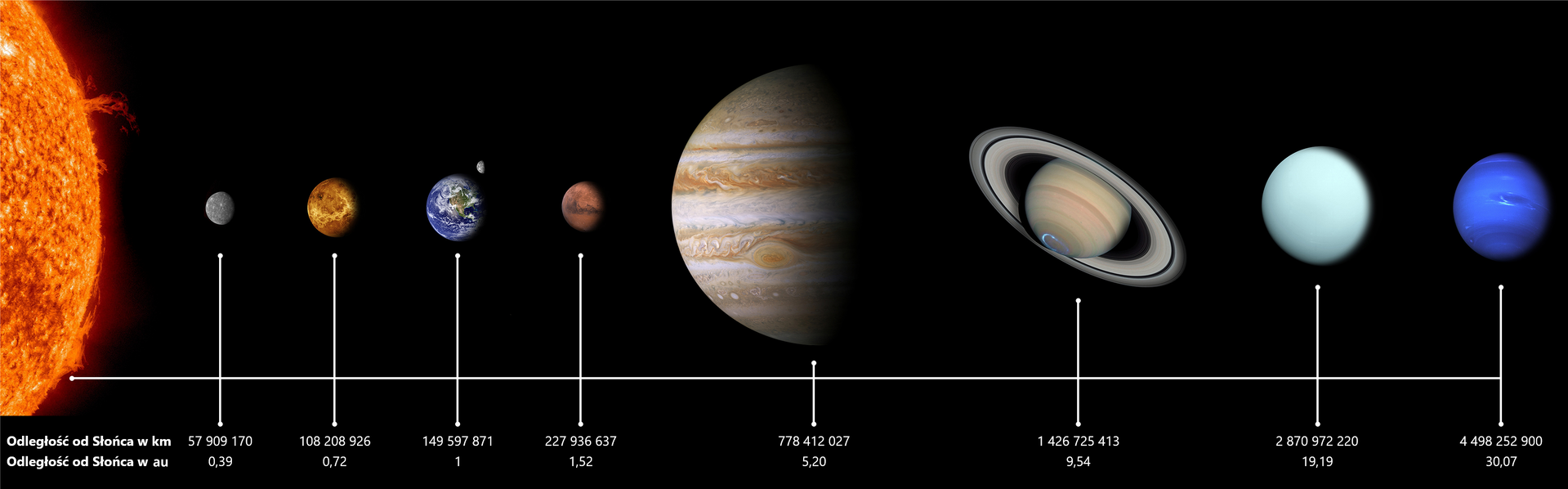
planeta | odległość | odległość |
|---|---|---|
Merkury | ||
Wenus | ||
Ziemia | ||
Mars | ||
Jowisz | ||
Saturn | ||
Uran | ||
Neptun |
Parsek to jednostka, której nazwa pochodzi od metody wyznaczania odległości – paralaksy. Jest to efekt patrzenia na ten sam obiekt z różnych kierunków, związany – w tym przypadku – z ruchem Ziemi wokół Słońca. oznacza odległość, dla której paralaksa całego rocznego okresu obiegu Ziemi jest kątem o wielkości sekundy. to inaczej (roku świetlnego).
Na podstawie wcześniejszych informacji, oblicz ile i ile metrów to .
Rozwiązanie:
Zapisujemy dane:
Obliczamy wartość parseka w metrach:
czyli –
–
Obliczamy wartość parseka w :
–
–
Oprócz stosowania specjalnych jednostek, warto przedstawić Układ Słoneczny w znanych i używanych na co dzień jednostkach, np. centymetrach lub metrach, ale w odpowiedniej skali. Skala informuje ile razy dany obiekt został pomniejszony w odniesieniu do rzeczywistych rozmiarów. Najczęściej przedstawiana jest jako stosunek rozmiaru na danej grafice lub mapie do rozmiaru w rzeczywistości np. skala mówi, że dany obiekt przedstawiony jest w –krotnym pomniejszeniu. Jaka skala byłaby jednak odpowiednia do przedstawienia Układu Słonecznego? Spróbujemy zamienić jednostki astronomiczne na metry. Zakładamy zatem, że przedstawimy jako . Dzięki temu uzyskamy skalę . Ponieważ odległość Ziemi od Słońca wynosi to w naszym pomniejszeniu byłby to . Odległość Neptuna od Słońca to jednak , co da aż metrów. Nie łatwo byłoby stworzyć taki model. Przedstawienie graficzne Układu Słonecznego jest trudne i większość grafik nie zachowuje skali (Neptun musiałby być przedstawiany w odległości razy większej niż Ziemia od Słońca).

Czy da się zatem stworzyć dobry model przyjmując ciała niebieskie jako bardzo małe? Swoją skalę zatytułowaną „Co gdyby Księżyc był wielkości jednego piksela” zaproponował amerykański projektant, grafik i pisarz Josh Worth. Stworzył on stronę internetową będącą modelem Układu Słonecznego przewijaną w poziomie od Słońca aż do ostatniej planety z założenia, że wielkość Księżyca wynosi piksel (, ang. pixel) piksel (, ang. pixel) i wielkości pozostałych planet i odległości są proporcjonalne. Piksel to najmniejszy element obrazu wyświetlany na ekranie monitora lub najmniejszy element drukowany cyfrowo. Standardowe drukarki atramentowe drukują w rozdzielczości – oznacza to, że w znajduje się . Rozdzielczość monitora w technologii Full HD na . W założeniu modelu Josha Wortha jednym takim pikselem miał być Księżyc. Średnica Księżyca wynosi , a zatem tej wielkości odpowiada jeden piksel w zastosowanej skali.
Oblicz, ile pikseli wynosi średnica Ziemi, a ile średnica Jowisza, jeśli średnica Księżyca to . Oblicz (też w pikselach) odległość od Księżyca do Ziemi i od Ziemi do Słońca.
Rozwiązanie:
Zapisujemy dane:
średnica Księżyca –
średnica Ziemi –
średnica Jowisza –
odległość Ziemia–Księżyc –
odległość Ziemia–Słońce –
Układamy proporcje.
Obliczenie średnicy Ziemi:
Obliczenie średnicy Jowisza:
–
Obliczenie odległości Ziemia – Księżyc:
–
Obliczanie odległości Ziemia – Słońce:
–
Wyniki podajemy jako liczby całkowite, piksele traktujemy jako najmniejsze, a więc i niepodzielne elementy obrazu cyfrowego.
Jak widzimy na powyższym przykładzie, modele Ziemi i Księżyca, jak i wielkości planet można bez problemu przedstawić nawet na małej grafice o niskiej rozdzielczości. Przedstawienie odległości planet od Słońca byłoby już większym problemem. Zakładając, że rozdzielczość monitora to na , aby pokazać w pikselach odległość od Ziemi do Słońca, potrzeba monitorów ustawionych jeden obok drugiego wyświetlających kontynuowany obraz. W druku wielkoformatowym stosuje się niskie rozdzielczości rzędu , grafika o rozmiarze mogłaby być wydrukowana jako metrowy obraz. Wielkość Słońca i planet Układu Słonecznego i ich odległość od Słońca przy założeniu, że wielkość Księżyca to wyglądałyby jak w poniższej tabeli.
Obiekt | odległość od Słońca w | odległość od Słońca w pikselach | średnica obiektu w | średnica obiektu w pikselach |
|---|---|---|---|---|
Słońce | ||||
Merkury | ||||
Wenus | ||||
Ziemia | ||||
Mars | ||||
Jowisz | ||||
Saturn | ||||
Uran | ||||
Neptun |
Model Josha Wortha „If the Moon Were Only 1 Pixel” dostępny jest w Internecie.
Aby przebyć drogę od Słońca do Neptuna trzeba bardzo długo przesuwać pikselową przestrzeń kosmiczną.
Księżyc to
Zapoznaj się z symulacją, a następnie wykonaj polecenia. Symulacja prezentuje względne rozmiary Księżyca i Ziemi oraz podaje ich wzajemną odległość w modelu, w którym Księżyc wyobrażamy sobie kolejno jako: kulę bilardową, piłkę do tenisa stołowego, ziemnego, siatkówki oraz jako 1 piksel.
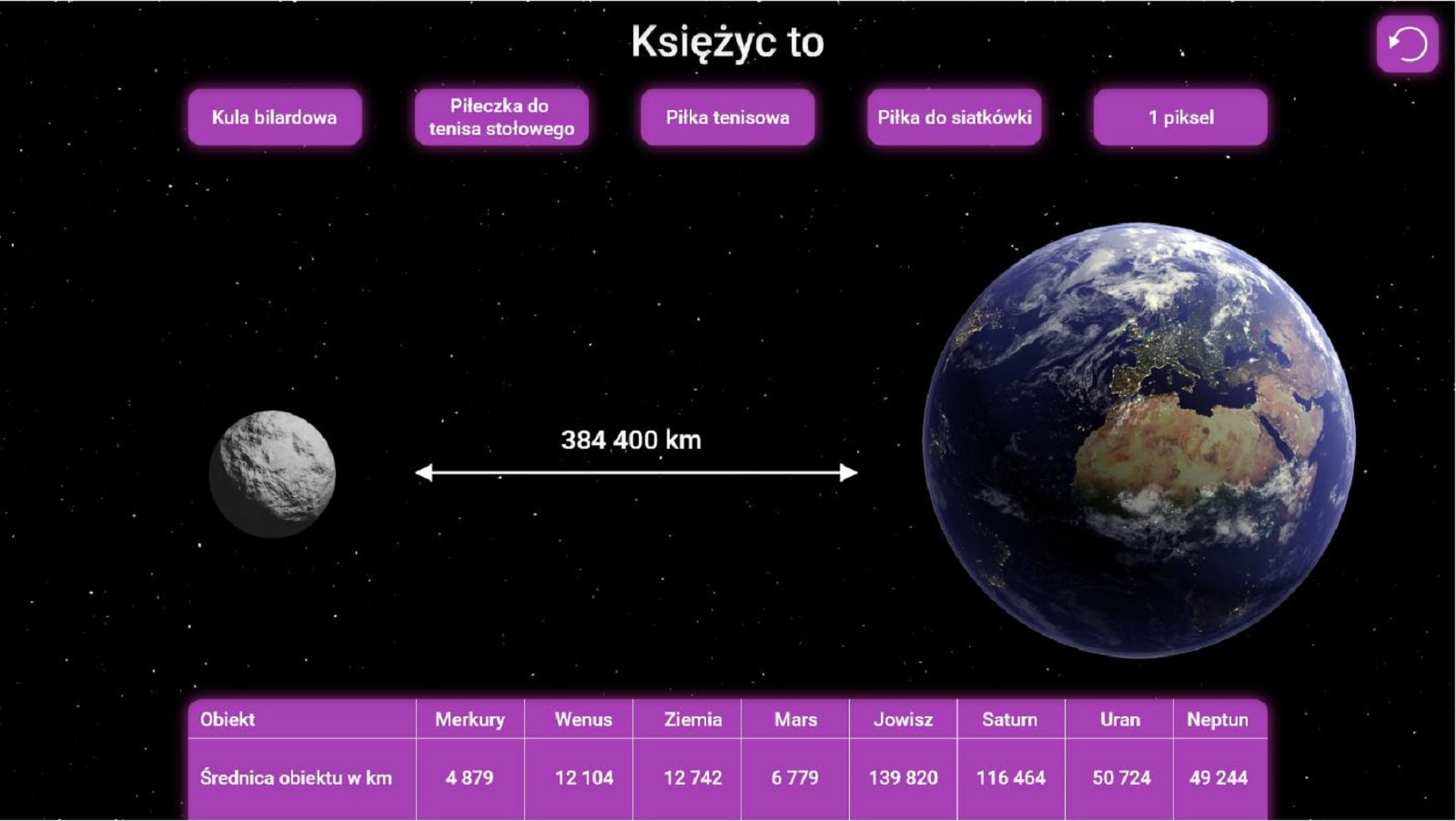
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P1HsdEQ3y
Zapoznaj się z tabelą, a następnie wykonaj polecenia.
Księżyc to | odległość Ziemia–Księżyc | średnica Merkurego | średnica Wenus | średnica Ziemi | średnica Marsa |
|---|---|---|---|---|---|
Księżyc | |||||
kula bilardowa | |||||
piłeczka do tenisa stołowego | |||||
piłka tenisowa | |||||
piłka do siatkówki | |||||
jeden piksel |
Księżyc to | średnica Jowisza | średnica Saturna | średnica Urana | średnica Neptuna |
|---|---|---|---|---|
Księżyc | ||||
kula bilardowa | ||||
piłeczka do tenisa stołowego | ||||
piłka tenisowa | ||||
piłka do siatkówki | ||||
jeden piksel |
Boisko do piłki nożnej ma metrów długości. Czy da się na takim boisku zbudować model Układu Słonecznego, z zachowaniem proporcji odległości między planetami, jeśli Księżycem będzie piłka do tenisa? Notatki i obliczenia możesz zapisać w polu poniżej.
Boisko do piłki nożnej ma metrów długości. Zaproponuj czym mógłby być Księżyc lub Ziemia, aby model Układu Słonecznego zmieścił się na boisku do piłki nożnej (z pominięciem rozmiaru Słońca). Notatki i obliczenia możesz zapisać w polu poniżej.
Boisko do piłki nożnej ma metrów długości. Jakie wymiary miałyby planety Układu Słonecznego, gdyby Księżyc był wielkości boiska? Notatki i obliczenia możesz zapisać w polu poniżej.
Sprawdź się
Zapisz w notacji wykładniczej:
,
,
,
Obliczenia i odpowiedź zapisz w polu poniżej.
Jaki jest stosunek wielkości człowieka o wysokości , do przedstawionego na obrazku obiektu? Obliczenia i odpowiedź zapisz w polu poniżej.

Tydzień świetlny, to odległość jaką przebywa światło w ciągu: Możliwe odpowiedzi: 1. dekady, 2. dni, 3. roku, 4. miesiąca
Słownik
() równa średniej odległości między Ziemią a Słońcem, przyjęta jako ; jest najwygodniejszą jednostką w Układzie Słonecznym.
(, skrót od wyrażenia paralaksa sekundowa) – dla gwiazdy odległej o parsek, kąt paralaksy heliocentrycznej wynosi jedną sekundę kątową; jednostki tej używają głównie astronomowie, aby wyrazić odległość do gwiazd i innych odległych obiektów astronomicznych.
(, od ang. pixel) – pojedynczy, najmniejszy, niepodzielny element obrazu cyfrowego (punkt na ekranie monitora).
() odległość, jaką światło przebywa w próżni w ciągu jednego roku; jeżeli wyrażamy odległości w latach świetlnych, wiemy jednocześnie, ile lat wcześniej zdarzyło się to, co obecnie obserwujemy.
Bibliografia
Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., 2017, Świat fizyki, Warszawa, WSiP