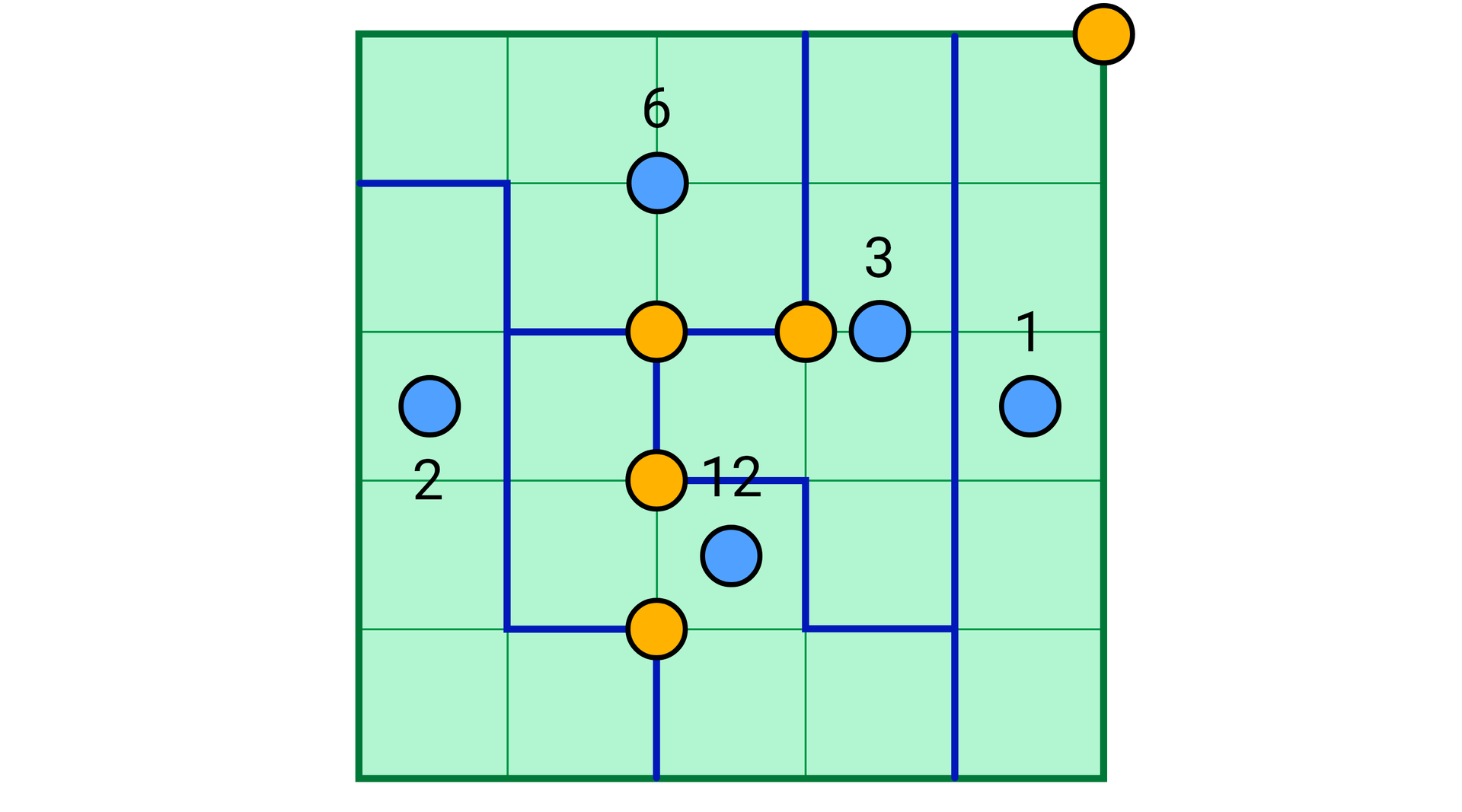
Geometria płaska
W lekcji geometrii płaskiej czekają do rozwiązania zadania wykorzystujące wiedzę dotyczącą figur takich jak trójkąty, kwadraty, prostokąty oraz koła. Dzięki ich własnościom, jak długość boków, kąty, obwody i pola powierzchni będziesz w stanie poradzić sobie z poniższymi ćwiczeniami.
Polecenie 1
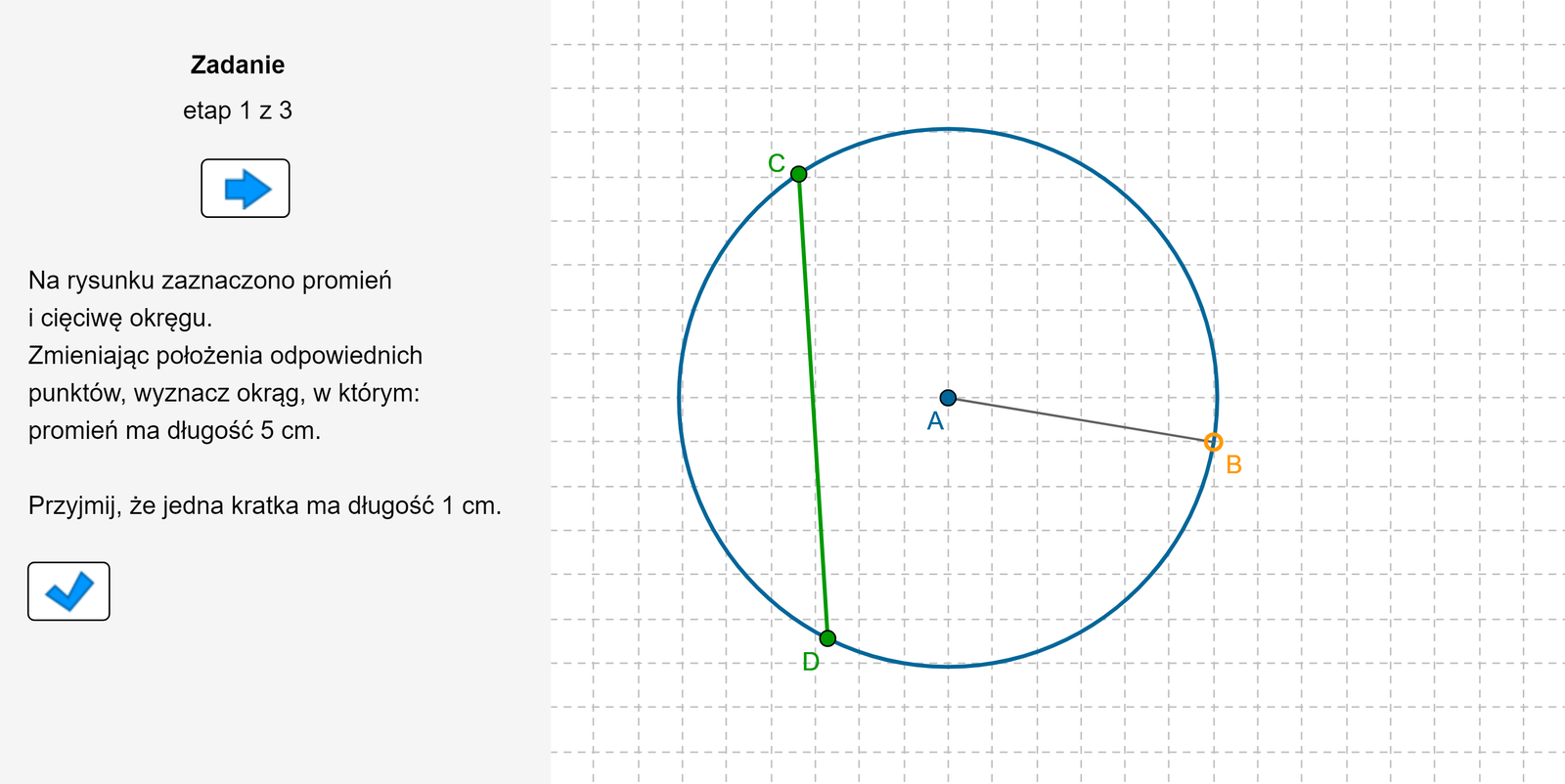
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 2
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 2
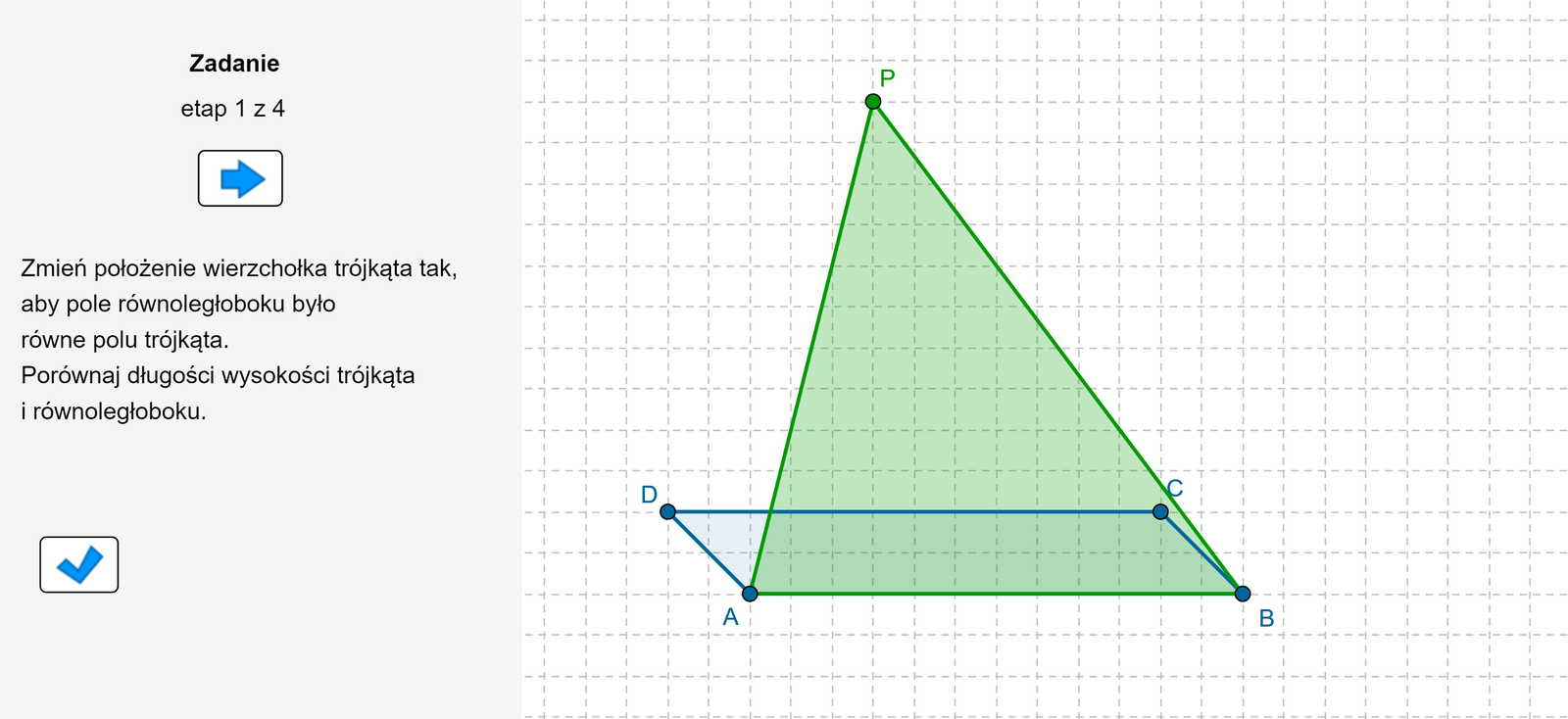
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
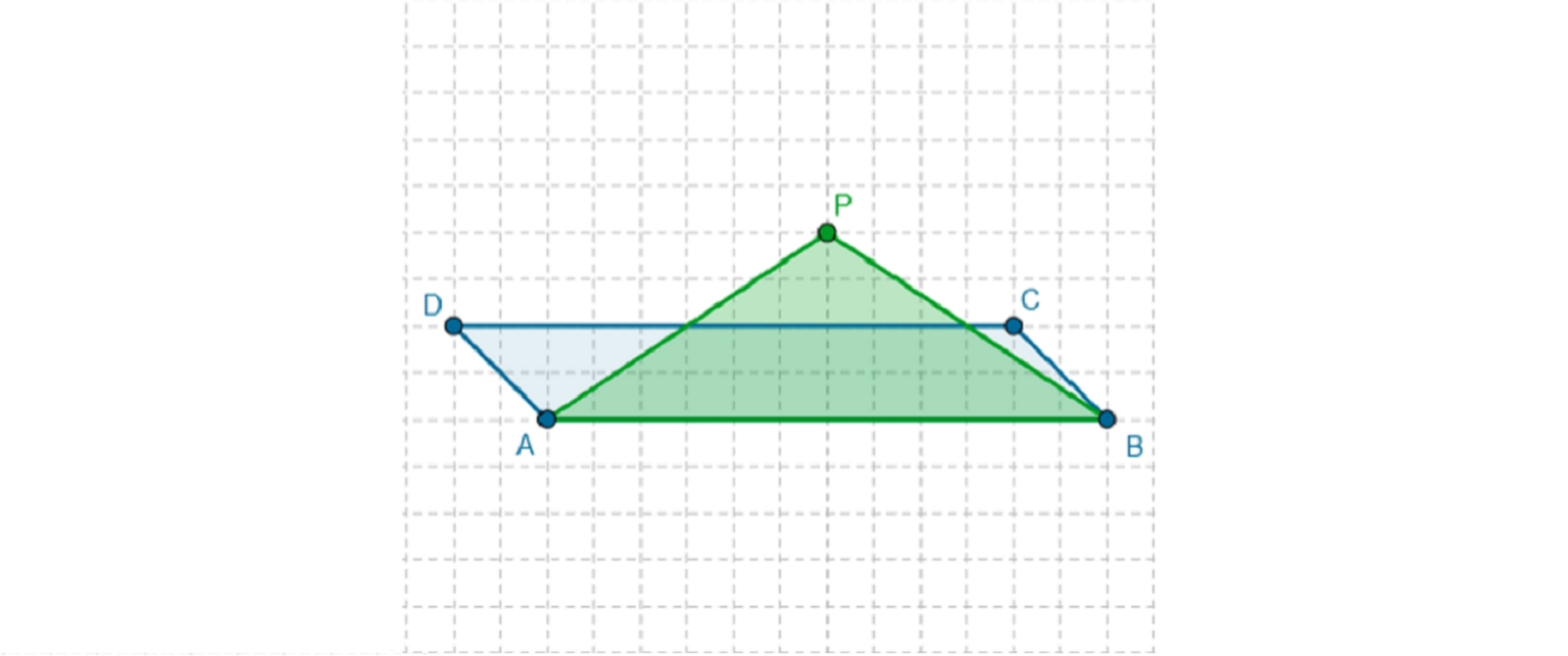
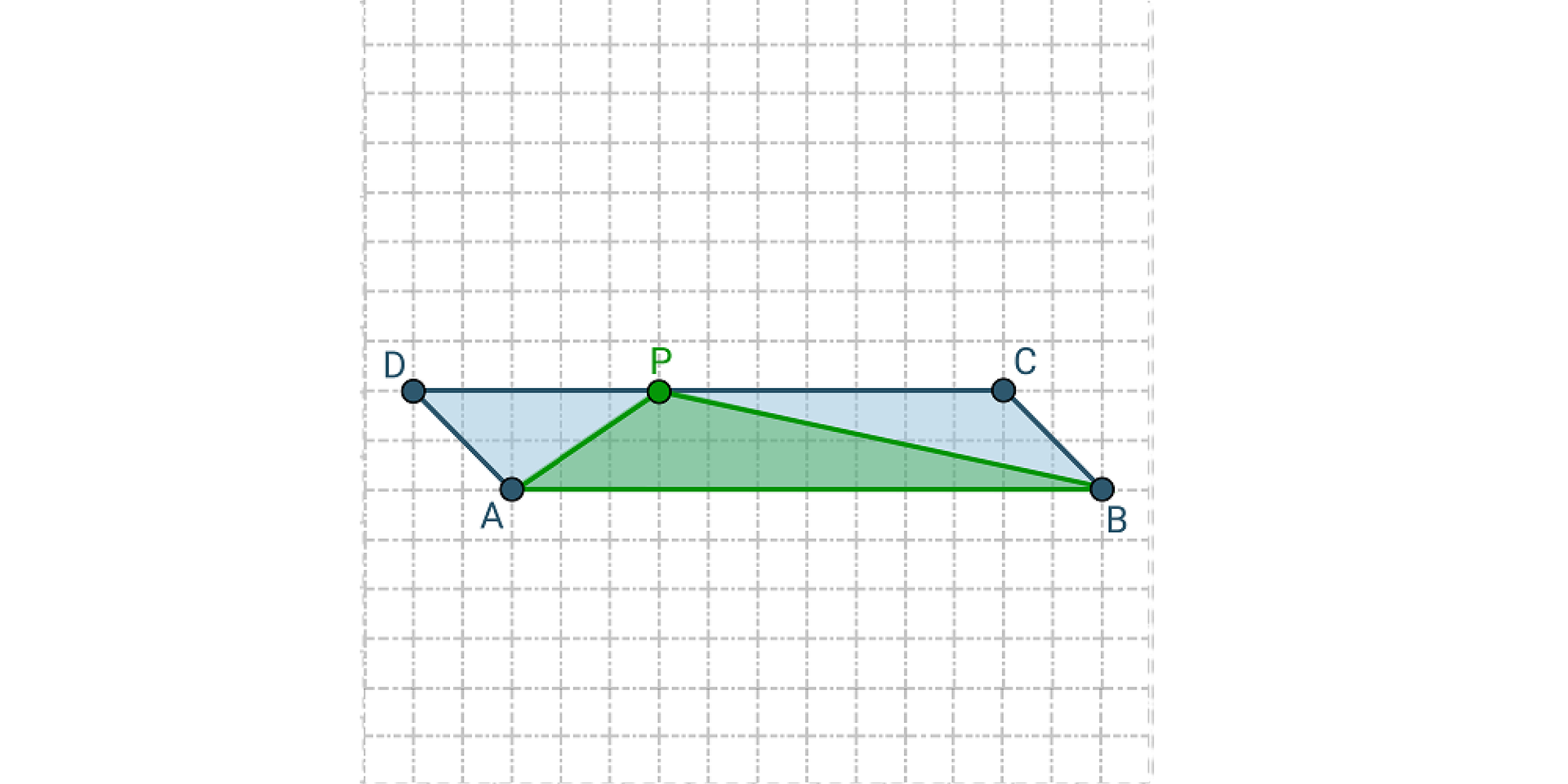
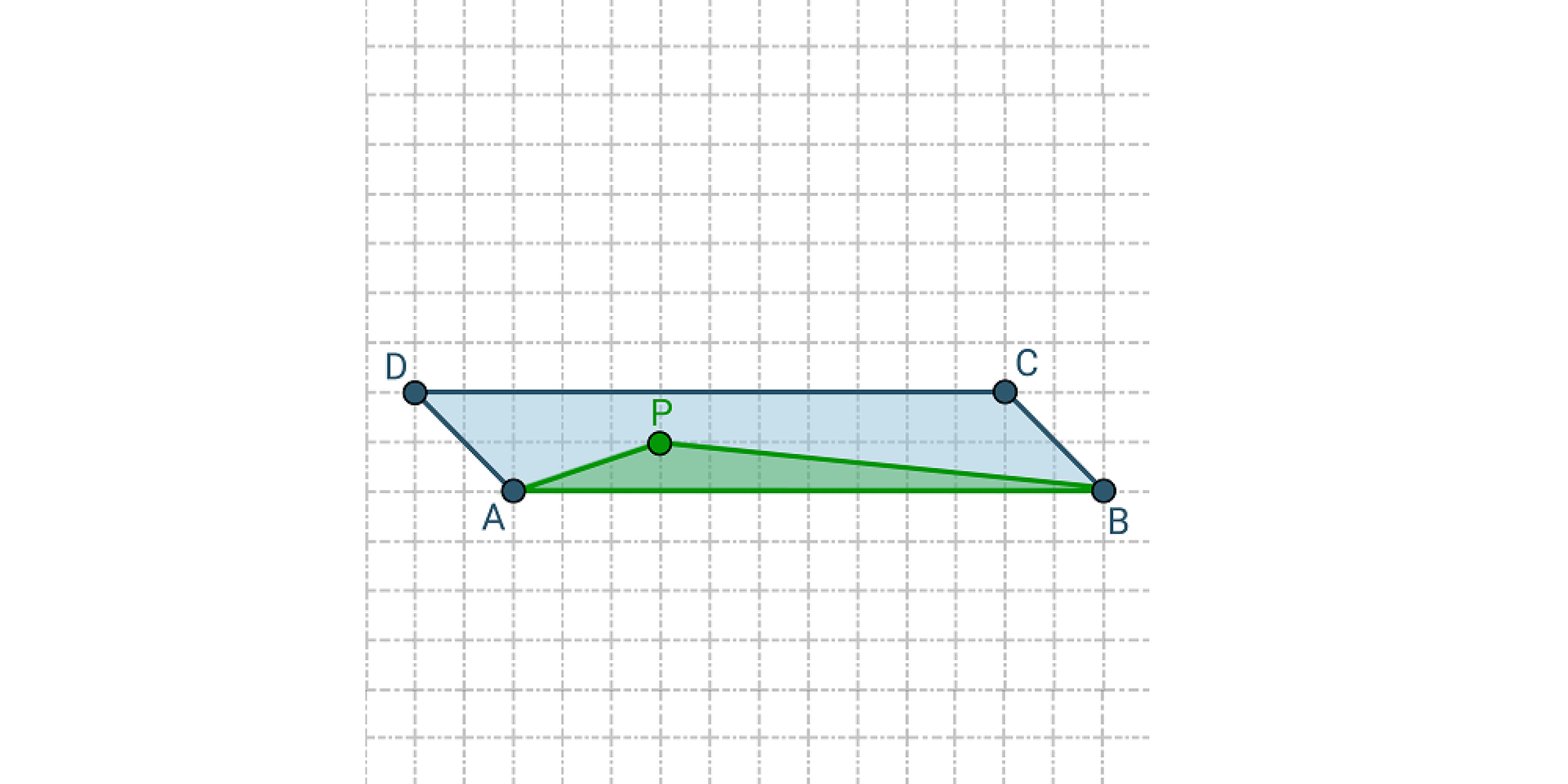
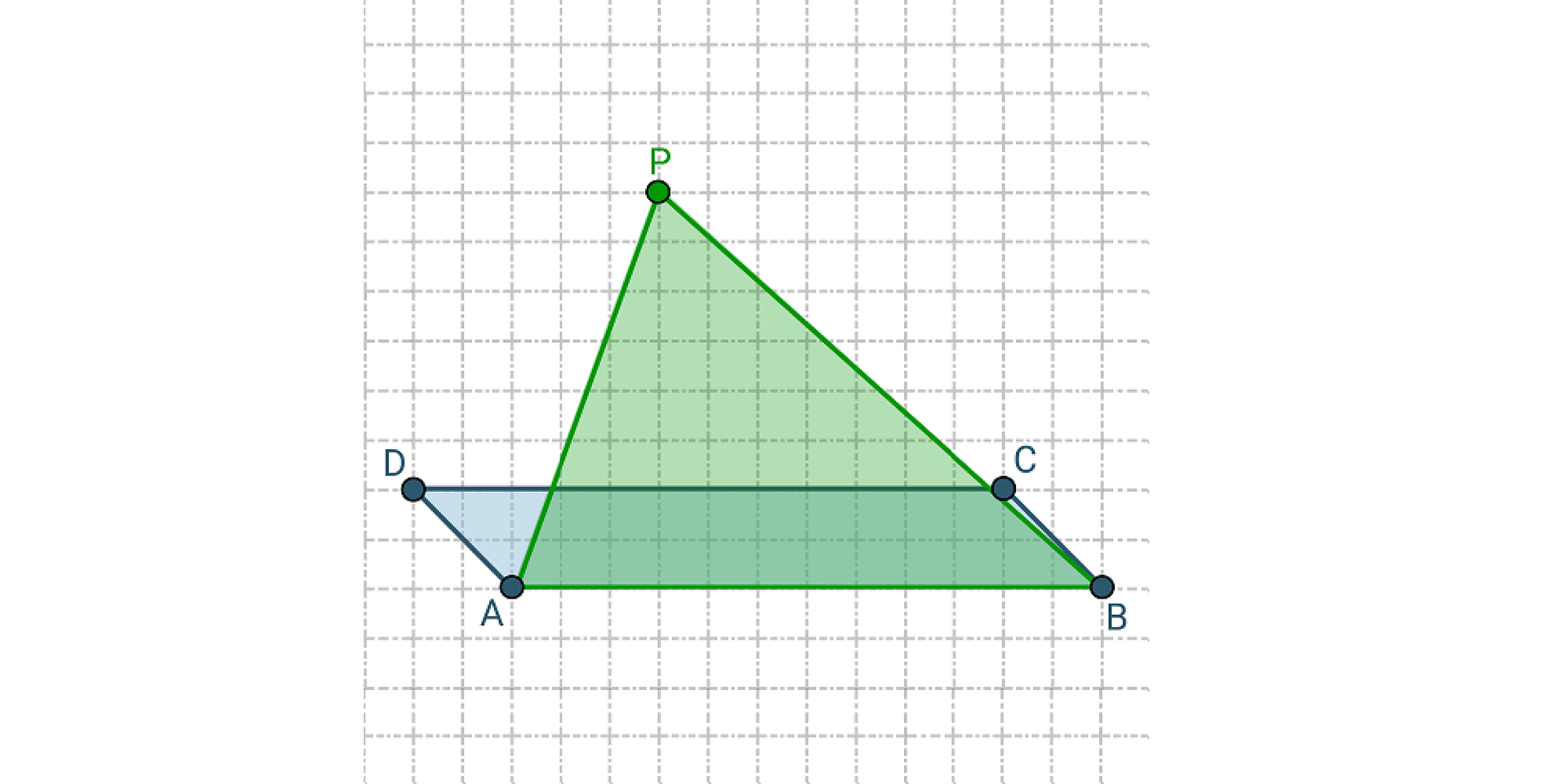
Gdy wysokości trójkąta i równoległoboku są sobie 1. mniejsze, 2. wysokość, 3. cztery, 4. równoległoboku, 5. dwa, 6. trójkąta, 7. osiem, 8. trzy, 9. równe, 10. większa to pole 1. mniejsze, 2. wysokość, 3. cztery, 4. równoległoboku, 5. dwa, 6. trójkąta, 7. osiem, 8. trzy, 9. równe, 10. większa jest dwa razy mniejsze od pola 1. mniejsze, 2. wysokość, 3. cztery, 4. równoległoboku, 5. dwa, 6. trójkąta, 7. osiem, 8. trzy, 9. równe, 10. większa.
Pole trójkąta jest dwa razy większe od pola równoległoboku gdy 1. mniejsze, 2. wysokość, 3. cztery, 4. równoległoboku, 5. dwa, 6. trójkąta, 7. osiem, 8. trzy, 9. równe, 10. większa trójkąta jest 1. mniejsze, 2. wysokość, 3. cztery, 4. równoległoboku, 5. dwa, 6. trójkąta, 7. osiem, 8. trzy, 9. równe, 10. większa razy większa od wysokości równoległoboku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 3
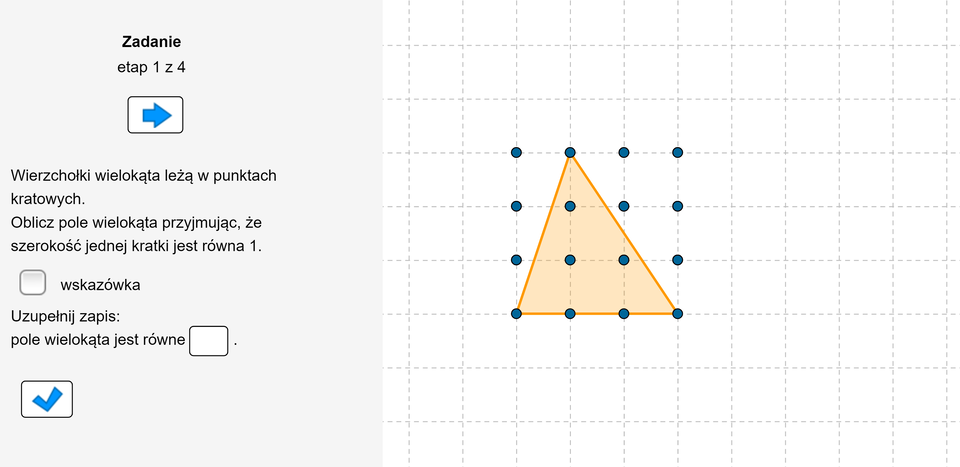
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 4
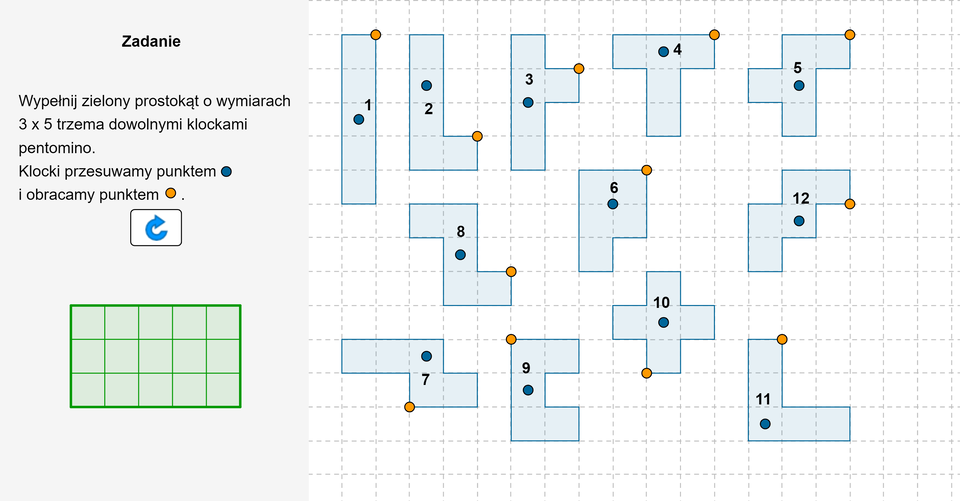
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 5
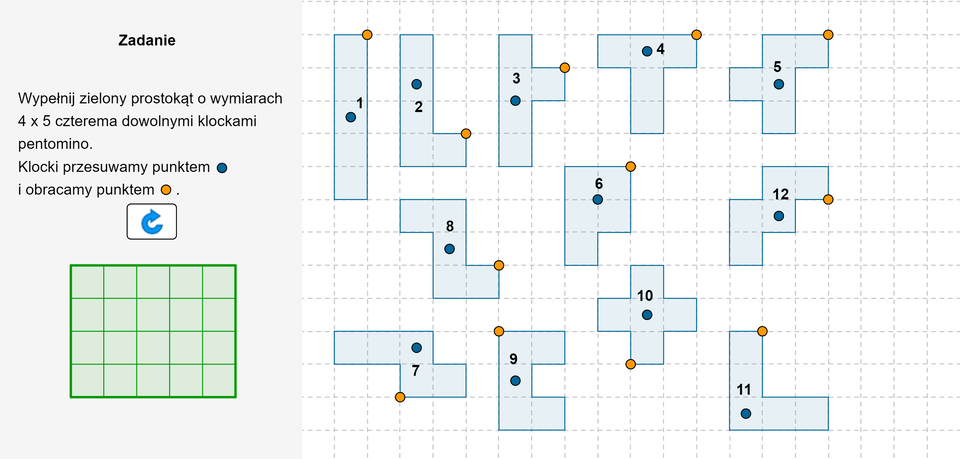
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 6
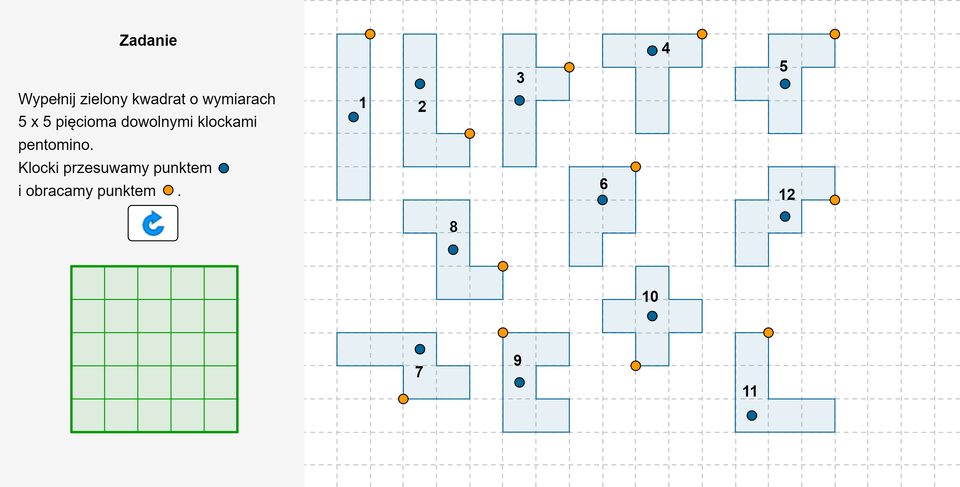
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
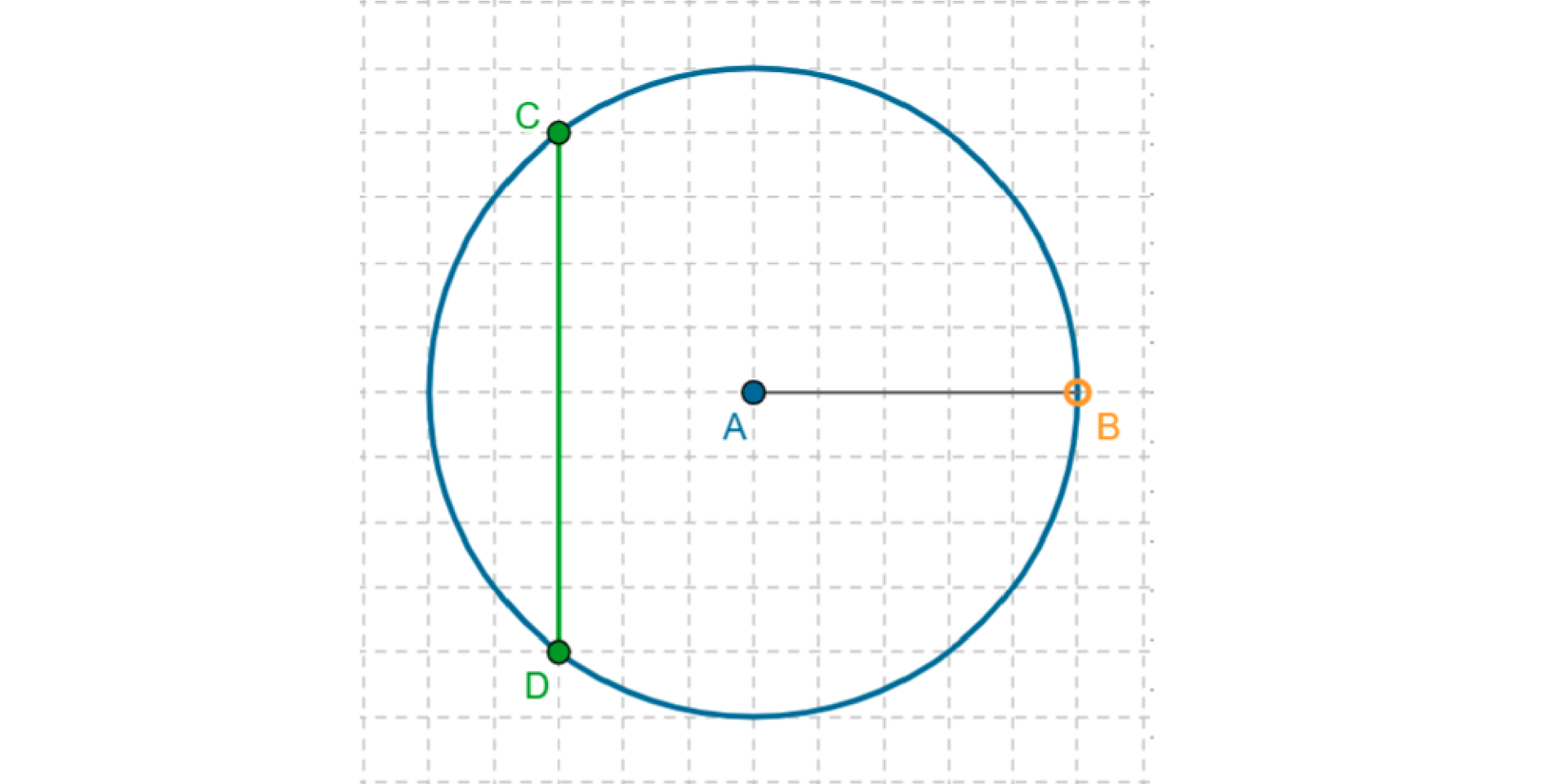
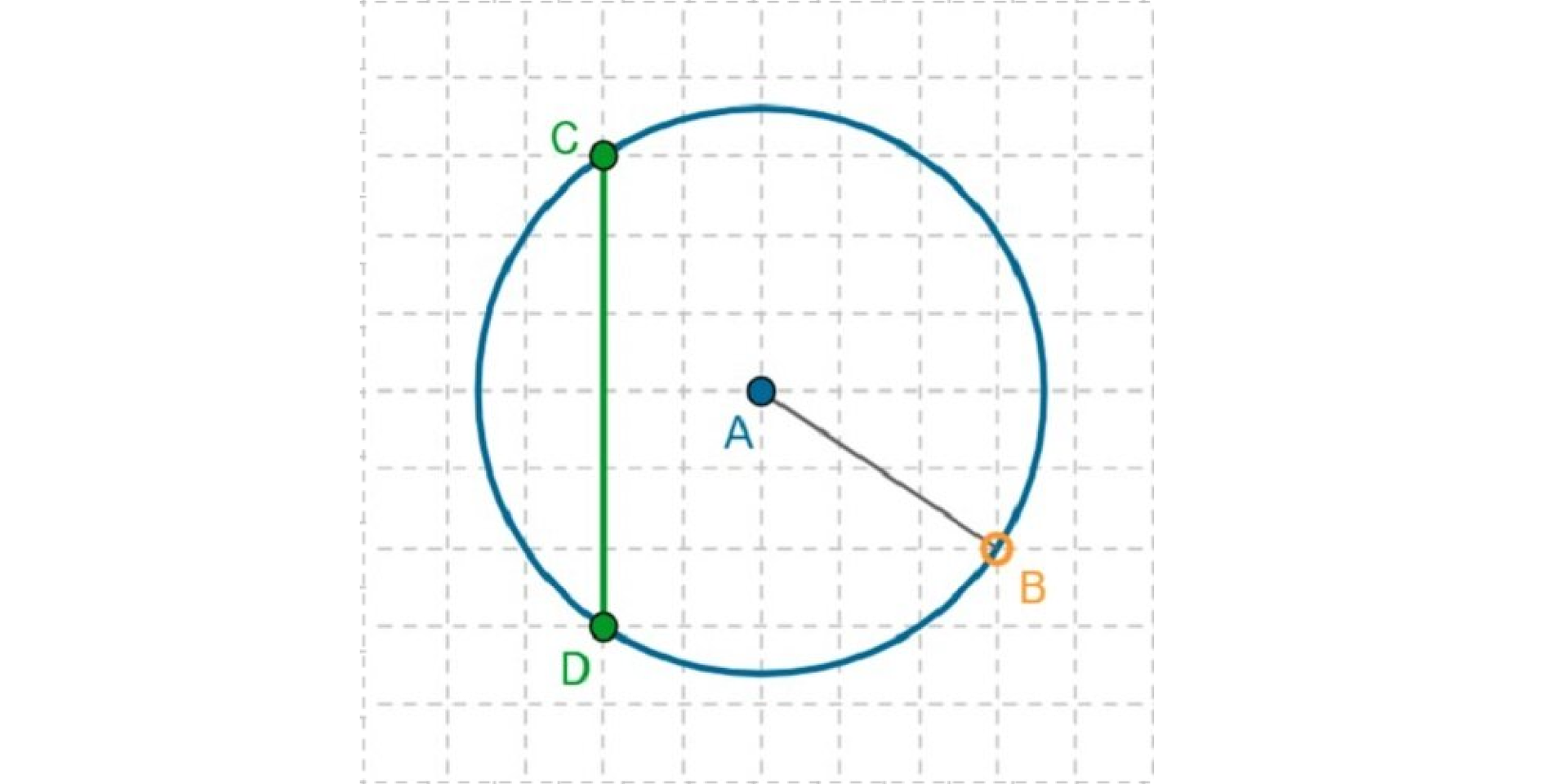
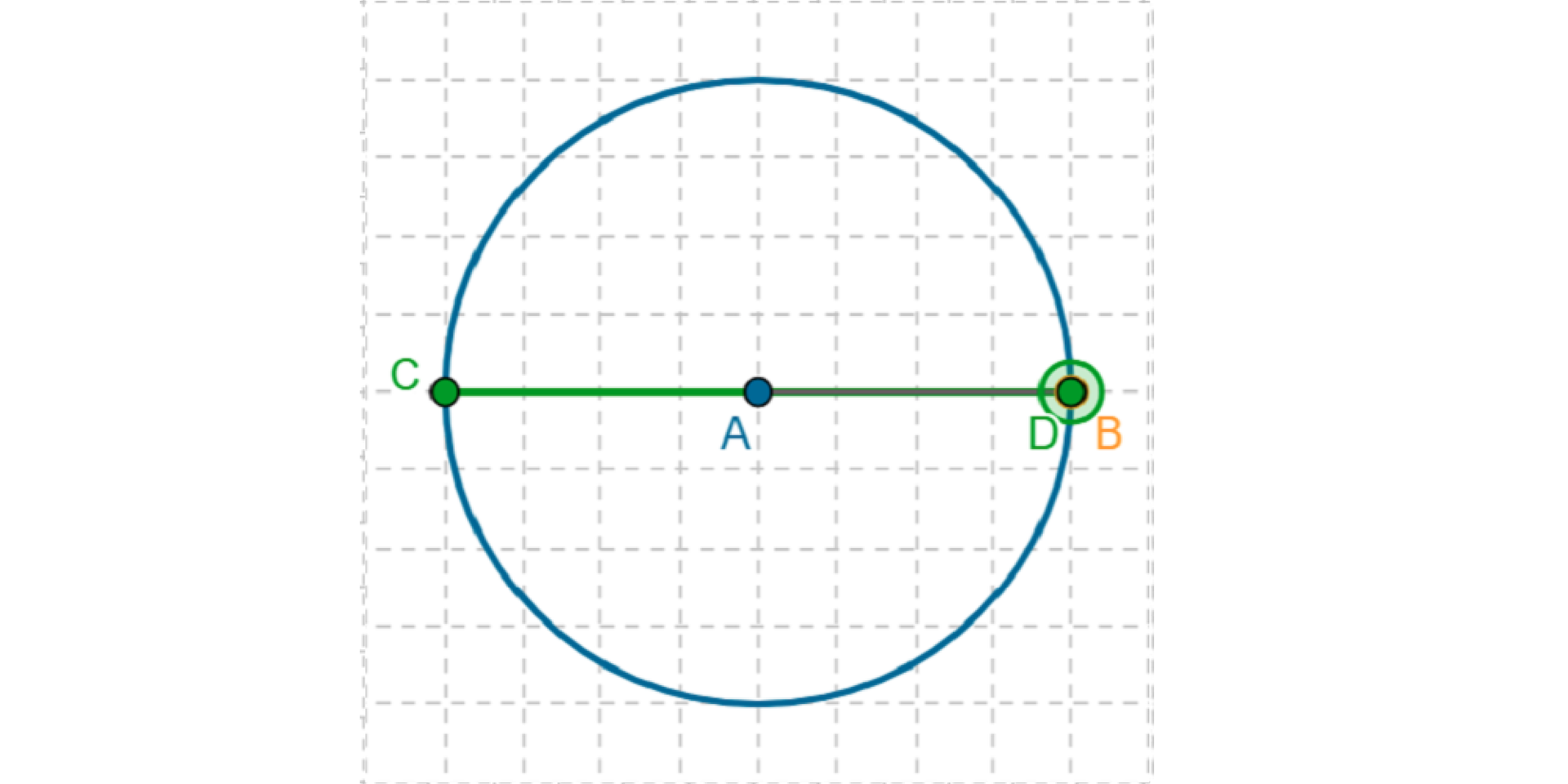
Przekątne w kwadracie dzielą się na 1. trójkącie, 2. trzy części, 3. równoramienny, 4. przekątne, 5. równoboczny, 6. okręgu, 7. boki, 8. pół, 9. kąty, 10. kwadratem, 11. równoległobokiem.
W 1. trójkącie, 2. trzy części, 3. równoramienny, 4. przekątne, 5. równoboczny, 6. okręgu, 7. boki, 8. pół, 9. kąty, 10. kwadratem, 11. równoległobokiem nie występują przekątne, tylko cięciwy.
Trójkąt 1. trójkącie, 2. trzy części, 3. równoramienny, 4. przekątne, 5. równoboczny, 6. okręgu, 7. boki, 8. pół, 9. kąty, 10. kwadratem, 11. równoległobokiem ma wszystkie 1. trójkącie, 2. trzy części, 3. równoramienny, 4. przekątne, 5. równoboczny, 6. okręgu, 7. boki, 8. pół, 9. kąty, 10. kwadratem, 11. równoległobokiem tej samej długości i 1. trójkącie, 2. trzy części, 3. równoramienny, 4. przekątne, 5. równoboczny, 6. okręgu, 7. boki, 8. pół, 9. kąty, 10. kwadratem, 11. równoległobokiem tej samej miary.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 7
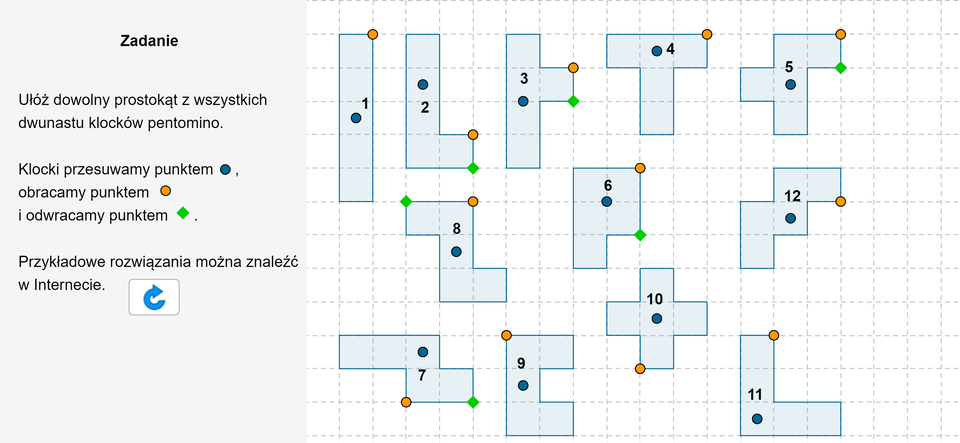
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBMMcPUA5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Wykorzystaj poniższy dzienniczek do zapisania swoich notatek lub przemyśleń.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.