Jak daleko jest do planet, Słońca i gwiazd?

R1JMBxtQiakmG

Zdjęcie przedstawia koronę słoneczną. Całe tło zdjęcia jest czarne. W centralnej części zdjęcia znajduje się czarne koło. Obręcz koła jest widoczna. Wokół krawędzi koła rozchodzą się świecące gazy. Gazy tworzą świetlisty obłok wokół koła. Obłok jest półprzeźroczysty. Gdzieniegdzie wokół krawędzi koła znajdują się czerwone plamy.

Na czym polega zjawisko paralaksy

Skąd wiemy, jak daleko od nas znajduje się jakaś rzecz? Pomińmy przedmioty znajdujące się w naszym najbliższym otoczeniu i zajmijmy się oceną odległości od domów, drzew, samolotów. Wykorzystujemy tu właściwości atmosfery i oka – im dalej znajduje się dany obiekt, tym bardziej jest on zamglony. Ma również mniejsze rozmiary kątowe. Jeśli przedmiot znajduje się blisko nas, widzimy dużo szczegółów, jeśli daleko – tylko ogólny zarys. Na ogół widujemy przedmioty i z bliska, i z daleka, dzięki czemu mamy skalę porównania. Brakuje nam jej jednak w odniesieniu do Księżyca, Słońca i gwiazd, gdyż są one one zbyt daleko. Gwiazdy (poza Słońcem) widzimy jako punkty niezależnie od tego, w jakiej odległości od nas się znajdują. Warto wspomnieć, że głównymi przeszkodami w rozwoju astronomii obserwacyjnej były brak możliwości pomiaru odległości i nieuwzględnianie skutków ruchu obrotowego Ziemi.

W wyznaczaniu odległości pomocne okazało się zjawisko paralaksyparalaksa (zjawisko)zjawisko paralaksy. Na rysunku poniżej widać, że gdy patrzymy z punktu $A$, chmurkę widzimy w miejscu, oznaczonym jako $1$, a gdy patrzymy z punktu $B$ – widzimy ją w zupełnie innym miejscu (oznaczonym jako $2$). Przesunięcie obserwatora z punktu $A$ do $B$ powoduje przesunięcie obrazu obiektu oglądanego przez tego obserwatora z położenia pierwszego do drugiego.

R1NpLnighKMWy

Grafika ilustruje zasadę, że gdy przesuwamy się z jednego położenia do drugiego to bliski przedmiot pozornie przemieszcza się względem tych położonych dalej. Tło jest białe. U góry po lewej stronie znajduje się niebieski owal z mniejszym, szarym owalem w środku i podpisany jako A. U góry po prawej stronie znajduje się taki sam niebieski owal z szarym w środku podpisany jako B. Na samym dole znajduje się pięć niebieskich owali. Na pierwszym owalu narysowana jest chmura podpisana jako dwa. Na czwartym owalu licząc od lewej narysowana jest taka sama chmura i podpisana jako jeden. Na środku kadru widoczna jest chmura bez żadnego owalu. Od owalu w pozycji A, przez chmurę na środku, aż do chmury w położeniu nr jeden została pociągnięta linia. Taką samą linię pociągnięto od owalu w B, przez chmurę na środku, aż do chmury w położeniu nr dwa. Linie te pokazują, że obserwator w położeniu A zobaczy chmurę w położeniu nr 1, zaś po przesunięciu się do położenia B zobaczy tę samą chmurę w innym miejscu, w położeniu nr dwa.

To zjawisko przeważnie jest niekorzystne. Jest np. źródłem błędu odczytu wielkości fizycznych za pomocą mierników wskazówkowych. Gdy odczytujemy położenie wskazówki na tle skali, to oko umieszczone w punkcie $A$ widzi inną wartość niż oko znajdujące się w położeniu $B$. Podobny błąd popełniamy, kiedy odczytujemy temperaturę na skali termometru.

Błąd spowodowany zjawiskiem paralaksy pojawia się również w niektórych aparatach fotograficznych – zarejestrowany obraz jest przesunięty w stosunku do tego, co widzieliśmy w wizjerze.

Przesunięć gwiazd, które znajdują się bliżej Ziemi w stosunku do tych bardziej oddalonych spodziewano się od momentu ogłoszenia teorii Kopernika. W wyniku ruchu Ziemi dookoła Słońca powinniśmy obserwować przesuwanie się bliższych gwiazd na tle dalszych. Jednak niczego takiego w tamtych czasach nie stwierdzono. Dlaczego?

Przyjrzyjmy się uważnie rysunkowi powyżej. Gdyby przyjąć, że odległość $AB$ to średnica orbity Ziemi (czyli – w ujęciu teorii Kopernika – okręgu, po jakim nasza planeta porusza się dookoła Słońca), to przesunięcie ciała niebieskiego (naszej chmurki) na tle oddalonego obiektu jest tym mniejsze, im dalej ten obiekt się od nas znajduje. Przy bardzo dużych odległościach przesunięcie będzie niemierzalne. Wszystko zależy więc od dokładności pomiarowej użytych przyrządów (a ściślej – dokładności pomiaru małych kątów).

Co nam daje znajomość geometrii, czyli jak zmierzyć odległość do obiektów, do których nie można dotrzeć?

RTAWlLLMKjEbC

Grafika przedstawia schemat sposobu liczenia odległości od drzewa. Tło białe. Od lewej do prawej krawędzi, ciągnie się niebieska, pofalowana wstęga. Jest to schematyczne przedstawienie rzeki. Na środku, ponad rzeką, znajduje się drzewo liściaste. Poniżej dolnej krawędzi rzeki narysowany jest gruby odcinek będący podstawą trójkąta, którego wierzchołkiem jest wspomniane drzewo. Lewy koniec odcinka, a tym samym lewy wierzchołek trójkąta, podpisany jest jako A. Prawy koniec odcinka, a więc prawy wierzchołek trójkąta, podpisany jest jako B. Górny wierzchołek trójkąta, a zatem ten położony przy drzewie, oznaczony jest jako D. Kąty wewnątrz trójkąta są podpisane następująco: przy wierzchołku A mamy kąt ${\beta }_1$, przy wierzchołku B jest ${\beta }_2$, a przy wierzchołku D jest kąt gamma. Od obu wierzchołków A i B idą pionowo do góry strzałki narysowane przerywaną linią i oznaczone jako N. Między taką strzałką, a bokiem trójkąta przy wierzchołku A znajduje się kąt ${\alpha }_1$, zaś między bokiem trójkąta a strzałką przy wierzchołku B znajduje się kąt ${\alpha }_2$.

Po drugiej stronie rzeki rośnie drzewo. W jakiej odległości od nas się ono znajduje?

Na brzegu rzeki, na którym stoimy, wyznaczamy tzw. bazę $AB$ – odcinek o długości kilkunastu lub kilkudziesięciu metrów. Im dalej od nas znajduje się drzewo, tym dłuższy powinien być ten odcinek.
Kiedy znajdujemy się w punkcie $A$, mierzymy kąt między kierunkiem północnym a kierunkiem, w jakim spoglądamy patrząc na drzewo. Czynność tę powtarzamy, kiedy znajdujemy się w punkcie $B$. Kierunek północny wyznaczony w punkcie $A$ jest równoległy do kierunku północnego wyznaczonego w punkcie $B$; oba te kierunki są prostopadłe do odcinka $AB$. Ten ostatni warunek nie jest konieczny, ale ułatwi rozumowanie tym, którzy jeszcze nie polubili geometrii.
Z pomiarów znamy wartości kątów ${\alpha }_1$ i ${\alpha }_2$. Z prostych zależności obliczamy wartości kątów ${\beta }_1$ i ${\beta }_2$ w trójkącie ABD i wartość kąta $\mathrm{\gamma }$$$. Znamy zatem wartości wszystkich kątów w tym trójkącie i długość jednego boku. Pozwala to obliczyć długości pozostałych boków.

A gdzie w tym wszystkim jest paralaksa?

No właśnie, pisaliśmy o pomiarze odległości do drzewa, a gdzie w tym wszystkim są paralaksa i gwiazdy?

Zacznijmy od powszechnie znanego faktu, że Ziemia krąży wokół Słońca.

Rcivc82b47HKD

Grafika ilustruje zmiany położenia gwiazdy G w stosunku do gwiazd odległych w wyniku ruchu obiegowego Ziemi. Tło białe. W dolnej części grafiki narysowane jest pomarańczowe koło podpisane dużą literą S i ilustrujące Słońce. Otacza je mocno spłaszczony okrąg symbolizujący orbitę Ziemi. Słońce znajduje się w jego centrum. Po jego prawej i lewej stronie Słońca, na wspomnianym okręgu narysowane są dwa jasnoniebieskie koła o podobnej wielkości co koło pomarańczowe. Symbolizują one położenia Ziemi na orbicie wokół Słońca w odstępie pół roku. Prawe z tych kół jest podpisane jako $Z_1$, zaś lewe jako $Z_2$. Nad Słońcem narysowane jest niewielkie koło symbolizujące jakąś gwiazdę i podpisane jako G. Wyżej, wzdłuż górnej krawędzi ilustracji, narysowane są kolejne cztery gwiazdy, położone dalej od Ziemi niż gwiazda G. Pierwsza z nich narysowana jest w lewym górnym rogu i oznaczona grecką literą epsilon. Kolejna znajduje się odrobinę na prawo od niej i podpisana jest jako sigma. Następna znajduje się ponad dwa razy dalej od gwiazdy epsilon niż gwiazda sigma i jest oznaczona literą eta. Ostatnia, oznaczona jako delta, znajduje się jeszcze odrobinę na prawo od gwiazdy eta. Od obu pozycji Ziemi poprowadzone są dwie równoległe do siebie półproste skierowane ku górze obrazka i odchylone o kilka stopni w prawo. Obie półproste narysowano przerywanymi liniami i oznaczono dużymi literami N. Obie pozycje Ziemi są ze sobą połączone odcinkiem, który przechodzi także przez Słońce. Jest to średnica orbity Ziemi. Od pozycji Ziemi $Z_2$ przez gwiazdę G pociągnięto półprostą, która dalej przechodzi między gwiazdami eta i delta. Również od pozycji Ziemi $Z_1$ przez gwiazdę G poprowadzono inną półprostą, która przechodzi następnie tuż po prawej stronie gwiazdy sigma. Średnica orbity Ziemi razem z przecinającymi się w gwieździe G półprostymi $Z_2$ G i $Z_1$ G tworzy trójkąt $Z_1$ $Z_2$ G. Między półprostą N a półprostą $Z_2$ G zaznaczono kąt ${\alpha }_1$. Kąt G $Z_2$ $Z_1$ oznaczono jako ${\beta }_1$. Między drugą półprostą N a półprostą $Z_1$ G zaznaczono kąt ${\alpha }_2$. Kąt G $Z_1$ $Z_2$ oznaczono jako ${\beta }_2$.

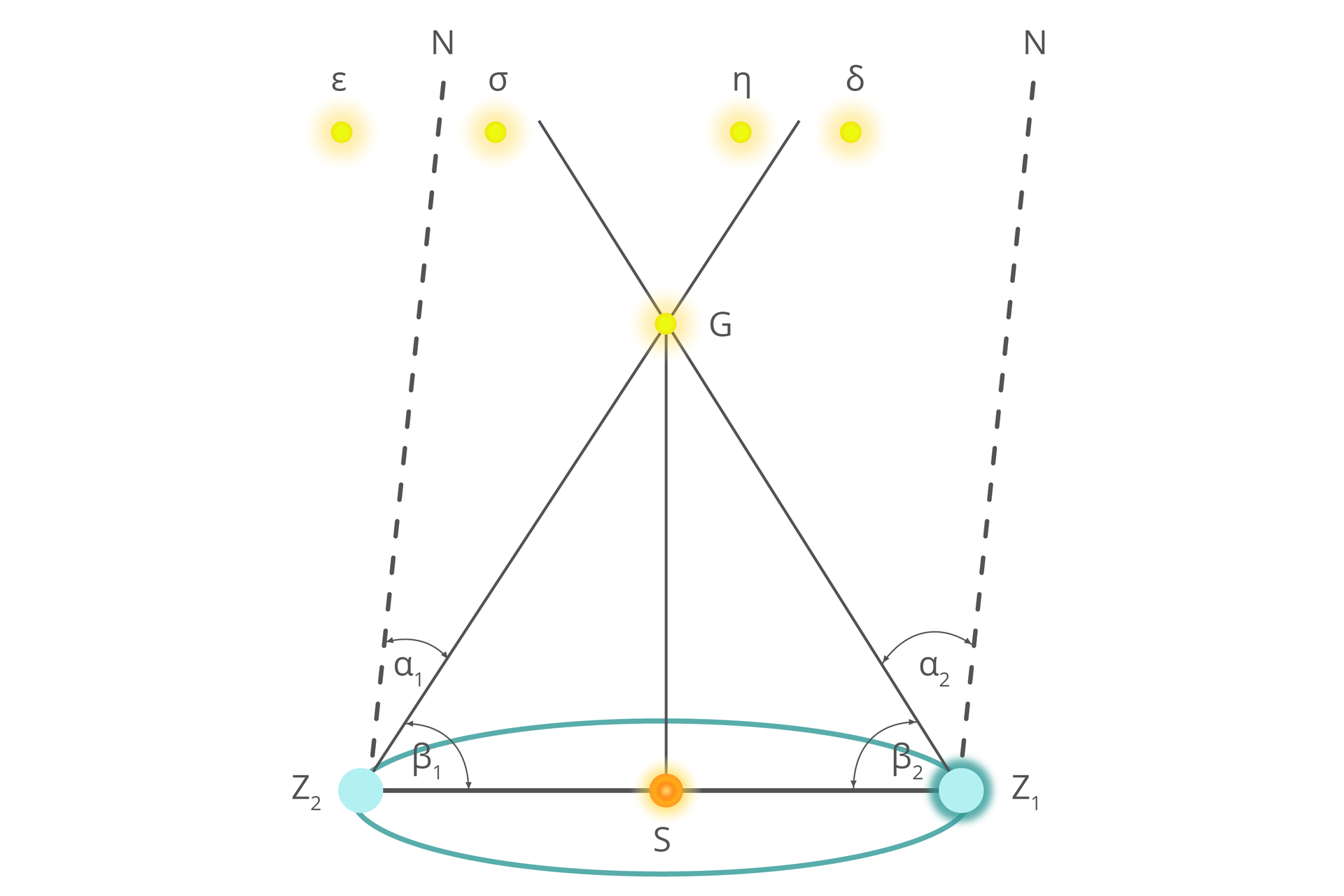
Jak widać na powyższej ilustracji, gwiazda $G$ w wyniku obiegu Ziemi dookoła Słońca stanie się widoczna obok gwiazdy $\sigma$ (sigma), gdy Ziemia znajdzie się w punkcie $Z_1$ orbity, oraz między gwiazdami $\eta$ (eta) i $\delta$ (delta), gdy będzie w położeniu $Z_2$ na orbicie. Takie zjawisko można zaobserwować w rzeczywistości.

Niestety, jest pewien problem: aby skorzystać z powyższej definicji i zmierzyć kąt paralaksykąt paralaksykąt paralaksy, należałoby polecieć tam, gdzie ta gwiazda się znajduje. Od najbliższej (poza Słońcem) gwiazdy światło biegnie do Ziemi przez ponad $4$ lata, a obecna technika pozwalałaby odbyć taką podróż w czasie dziesiątków tysięcy lat. Na szczęście nie musimy nigdzie lecieć, ponieważ dzięki własnościom geometrycznym trójkąta i poprzez pomiar kątów ${\alpha }_1$ i ${\alpha }_2$, możemy poznać wartość kąta paralaksy z Ziemi.

Aby zmierzyć kąt paralaksy dla gwiazd, trzeba było czekać do połowy $\mathrm{XIX}$ wieku – dopiero w $1839$ r. trzej astronomowie – Friedrich von Struve, Fridrich Bessel i Thomas Henderson – niezależnie od siebie wyznaczyli wartości kątów paralaksy dla kilku najbliższych gwiazd. Ich pomiary spowodowały zdjęcie dzieła Kopernika z indeksu ksiąg zakazanych. Wyznaczenie pierwszych paralaks dla gwiazd nie było jednak jedynym dowodem na ruch Ziemi dookoła Słońca. Ponad sto lat wcześniej, w latach $1725-26$, odkryto i wyjaśniono zjawisko aberracji światła gwiazdaberracja światła gwiazdaberracji światła gwiazd. Dokonał tego James BradleyJames BradleyJames Bradley.

Pomiary paralaksy są bardzo żmudnym zajęciem. W latach $1989-93$ satelita Europejskiej Agencji Kosmicznej, nazwany Hipparcos na cześć astronoma Hipparcha, dokonał pomiarów paralaksy dla około $2,5$ miliona gwiazd. Oprócz astrometrii satelita realizował również program fotometryczny, czyli pomiary natężenia światła pochodzącego od gwiazd. Wykrył duże liczby gwiazd podwójnych, a także zbadał zmiany promieniowania tysięcy gwiazd zmiennych. Do wyznaczenia paralaks potrzebna była dokładność rzędu $0,001$ sekundy łukusekunda kątowa, minuta kątowasekundy łuku. Aby wyobrazić sobie, jaka to wartość, wystarczy przypomnieć sobie, że kątowe średnice Słońca lub Księżyca na niebie wynoszą w przybliżeniu około pół stopnia, czyli $1800$ sekund kątowychsekunda kątowa, minuta kątowasekund kątowych.

Dlaczego tak trudno było wyznaczyć kąt paralaksy? Odległości do gwiazd okazały się znacznie większe, niż przypuszczano. Paralaksa najbliższej (poza Słońcem) gwiazdy wynosi około $0,78\text{'}\text{'}$ (sekundy kątowej). Jest to gwiazda o nazwie Proxima Centauri. Słowo „Proxima” oznacza po prostu „najbliższa”. Ta gwiazda znajduje się na południowej półkuli nieba, w gwiazdozbiorze Centaura. Razem z podwójną gwiazdą αalfa Centauri tworzy układ potrójny gwiazd.

Jakich jednostek używamy do opisu odległości gwiazd i planet?

Do opisu odległości astronomowie używają jednostki związanej bezpośrednio z kątem paralaksy. Ta jednostka to parsekparsekparsek ($1 \mathrm{pc}$) i oznacza ona odległość, z jakiej paralaksa roczna Ziemi widziana prostopadle do płaszczyzny jej orbity wynosi $1\text{'}\text{'}$, a jej przybliżona definicja przedstawia się następująco:

W powyższym wzorze $p$ to wartość kąta paralaksy obiektu, do którego odległość w parsekach chcemy obliczyć, podana w sekundach kątowych, zaś $D$ to obliczona odległość w parsekach. Przykładowo: paralaksa Proximy wynosi $0,78\text{'}\text{'}$, zatem jej odległość od Ziemi to:

Jest to wygodna jednostka – dwie najbliższe nam gwiazdy (Słońce i Proxima) są odległe od siebie ok. 1 parsek. Używane są też wielokrotności tej jednostki: kiloparsek ($\mathrm{kpc}$), megaparsek ($\mathrm{Mpc}$) i gigaparsek ($\mathrm{Gpc}$).

Dzięki trygonometrii, którą niedługo poznasz w szkole, można obliczyć ile kilometrów mieści się w jednym parseku. Otrzymujemy ogromną liczbę, tj. $\mathrm{3,086}{·10}^{13}\mathrm{ km}$ lub $\mathrm{3,086}·{10}^{16}\mathrm{m}$. Oznacza to, że odległość do Proximy wynosi około $40$ bilionów kilometrów.

Popularną jednostką używaną w artykułach popularnonaukowych jest jeden rok świetlnyrok świetlnyrok świetlny ($1 \mathrm{ly}$ – skrót od słów light year). Jest to odległość, jaką światło przebywa w próżni w ciągu roku. Łatwo obliczyć, jaka jest to odległość - może obliczycie ją sami?

Wiemy już, jak wyznaczyć odległość do gwiazd. Przyrządy satelity Hipparcos pozwalają wyznaczyć dokładne odległości do $1000 \mathrm{pc}$. Galaktyka jest jednak znacznie większa; znacznie większa jest także odległość do innych galaktyk. Jak się wyznacza tak ogromne odległości? Wspomnimy o tym w dalszej części podręcznika.

A Układ Słoneczny? Czy do wyznaczania odległości można wykorzystać inne metody? Odkrycie trzech praw Keplera opisujących ruch planet (zwłaszcza $\mathrm{III}$ prawa) pozwoliło obliczyć odległości od planet do Słońca. Przyjmijmy przy tym, że jednostka odległości równa $1$ odpowiada odległości między Ziemią a Słońcem. Taką jednostkę nazywamy jednostką astronomicznąjednostka astronomiczna $\left(1 \mathrm{au}\right)$jednostką astronomiczną. Jej wartość wynosi w przybliżeniu $149 600 000 \mathrm{km}$. Jednostkę astronomiczną oznaczamy jako $\mathrm{au}$ (astronomical unit). 1 parsek jest równy $206 265 \mathrm{au}$.

A jak wyznaczyć odległość z Ziemi do Księżyca? Opisane wyżej metody nie znajdują tu zastosowania – Księżyc znajduje się stosunkowo blisko Ziemi. Jest ona jednak kilkukrotnie od niego większa – można zatem wykorzystać pomiary wykonywane na Ziemi. W tym celu posługujemy się zjawiskiem paralaksy geocentrycznej.

R1aS23E9ZklUy

Grafika ilustruje paralaksę geocentryczną. Tło białe. Z lewej strony znajduje się duża grafika kuli ziemskiej. Po prawej stronie narysowany jest Księżyc, a za nim, tuż przy prawej krawędzi, 5 niewielkich kul symbolizujących gwiazdy, Są one ułożone na fragmencie okręgu o średnicy dużej na tyle, że przypomina on linie prostą, od góry do dołu w równych odstępach. Ze środka Ziemi do punktu położonego na krawędzi Ziemi na godzinie pierwszej zaznaczono promień planety. Od środka Ziemi poprowadzony jest odcinek styczny do górnej krawędzi Księżyca, jego koniec znajduje się tuż ponad jedną z gwiazd przy prawej krawędzi. Z punktu na krawędzi Ziemi, do którego poprowadzono promień, narysowano odcinek styczny zarówno do krawędzi Ziemi w tym punkcie, jak i do górnej krawędzi Księżyca. Koniec tego odcinek znajduje się tuż poniżej tej samej gwiazdy. Grafika ta pokazuje, że obserwator z jednego miejsca na powierzchni Ziemi zobaczy tę gwiazdę tuż przy krawędzi Księżyca, zaś obserwator w innym miejscu nie zobaczy tej gwiazdy, ponieważ z jego perspektywy będzie ona skryta za krawędzią Księżyca.

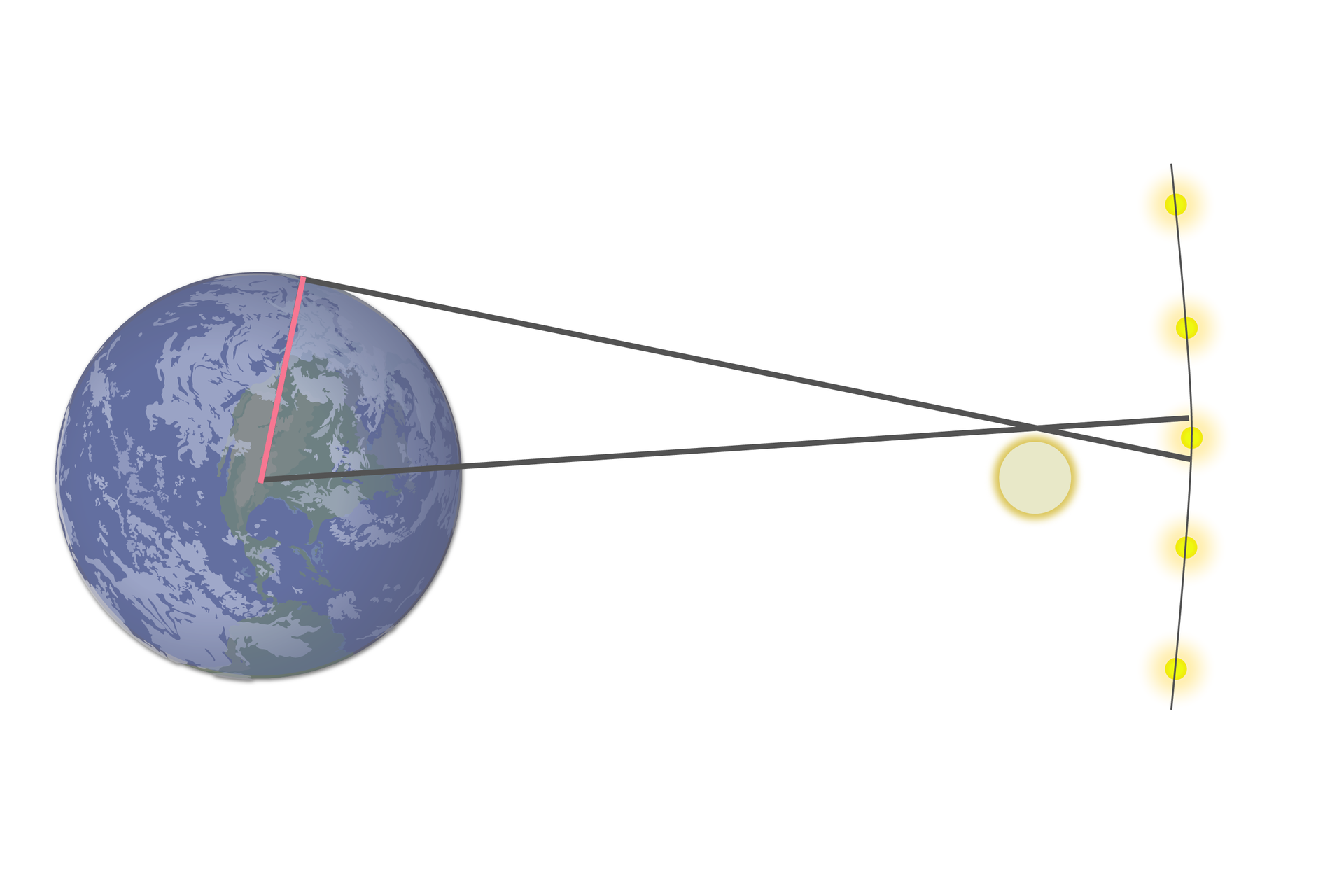
W tym samym momencie tarcza Księżyca ułożona jest inaczej względem gwiazd z perspektywy obserwatora (w pobliżu bieguna Ziemi), dla którego Księżyc znajduje się w płaszczyźnie horyzontu, a inaczej dla obserwatora (bliżej równika), dla którego Księżyc jest w zenicie. Wyznaczenie kątów w sposób podobny jak dla paralaksy heliocentrycznejparalaksa heliocentrycznaparalaksy heliocentrycznej pozwala wyznaczyć odległość do Księżyca.

Obecnie odległość do Księżyca wyznacza się za pomocą zjawiska odbicia światła laserowego wysłanego z Ziemi i odbitego od specjalnych odbłyśników umieszczonych na powierzchni naszego naturalnego satelity, m.in. dzięki wyprawom kosmicznym.
Orbita Księżyca jest orbitą eliptyczną. Minimalna odległość od Księżyca do Ziemi wynosi $356 500 \mathrm{km}$ (odległość do najbliższego perygeum), a maksymalna $406 700 \mathrm{km}$ (odległość do najdalszego apogeum). Połowa wielkiej osi elipsy wynosi około $384 700 \mathrm{km}$.

Podsumowanie

• Zjawisko paralaksy heliocentrycznej (czyli pozornego przesuwania się gwiazd znajdujących się bliżej Ziemi w stosunku do tych dalszych, co jest wynikiem zmiany położenia obserwatora) pozwoliło potwierdzić teorię Kopernika i wyznaczyć odległości do najbliższych gwiazd.

• W astronomii używane są różne jednostki, za pomocą których wyraża się odległość do gwiazd lub planet. W Układzie Słonecznym najwygodniejszą jednostką jest jednostka astronomiczna $\left(1 \mathrm{au}\right)$, równa średniej odległości między Ziemią a Słońcem, czyli $\mathrm{149\; 597\; 870\; 700} \mathrm{m}$. Astronomowie używają jednostki zwanej parsekiem (skrót od wyrażenia paralaksa sekundowa). Kąt paralaksy dla gwiazdy odległej o 1 parsek $\left(1 \mathrm{pc}\right)$ wynosiłby $1\text{'}\text{'}$. W życiu codziennym często używa się jednostki zwanej rokiem świetlnym $\left(1 \mathrm{ly}\right)$. Jest to odległość, jaką światło przebywa w próżni w ciągu jednego roku.

• Do wyznaczenia odległości obiektów znajdujących się stosunkowo blisko Ziemi, takich jak Księżyc czy planety Układu Słonecznego, wystarczają dwa punkty na Ziemi. Zmiana położenia obserwatora o kilka czy kilkanaście tysięcy kilometrów wystarczy do wykazania zjawiska paralaksy i wyznaczenia odległości.

Słownik

Biogram

James Bradley13.07.1762Chalford09.1692Sherborne

R1cUnZr5xLntG

Ilustracja przedstawia podobiznę Jamesa Brdleya. Mężczyzna w wieku ok. 45 lat. Widoczny prawy półprofil. Twarz okrągła. Karnacja jasna, widoczne rumieńce na policzkach. Czoło wysokie, gładkie. Brwi jasne. Oczy ciemne. Na głowie siwa peruka z lokami, sięgająca do ramion. Mężczyzna ubrany na czarno, pod szyją biały, podłużny kołnierz.

James Bradley

1692.9 Sherborne – 1762.07.13 Chalford

Bradley mierzył zmiany położenia gwiazd na niebie, przy czym te zmiany były dostrzegalne w cyklu rocznym. Badacz otrzymał jednakowe wyniki dla wszystkich gwiazd, które obserwował, zatem obserwowane zjawisko nie mogło być efektem paralaksy rocznej. Bradley interpretował je jako proces wynikający ze skończonej prędkości światła. W ten sposób wykazał dwie rzeczy: że Ziemia krąży dookoła Słońca i że prędkość światła jest skończona. W $1742$ r. James Bradley uzyskał tytuł Astronoma Królewskiego i do końca życia pracował oraz mieszkał w obserwatorium w Greenwich.