Jednomian kwadratowy i jego własności. Przesunięcie wykresu jednomianu kwadratowego wzdłuż osi układu współrzędnych
Analizując przykłady zawarte w tym materiale:
poznasz własności funkcji kwadratowej dla oraz dla ,
dowiesz się, jaki wzór i własności ma funkcja, której wykres otrzymano w przesunięciu wykresu funkcji kwadratowej wzdłuż osi układu współrzędnych,
poznasz własności krzywej, zwanej parabolą.
Rozwiązując ćwiczenia – sprawdzisz ukształtowane umiejętności
Jednomian kwadratowy i jego własności
Omówimy własności funkcji określonej wzorem .
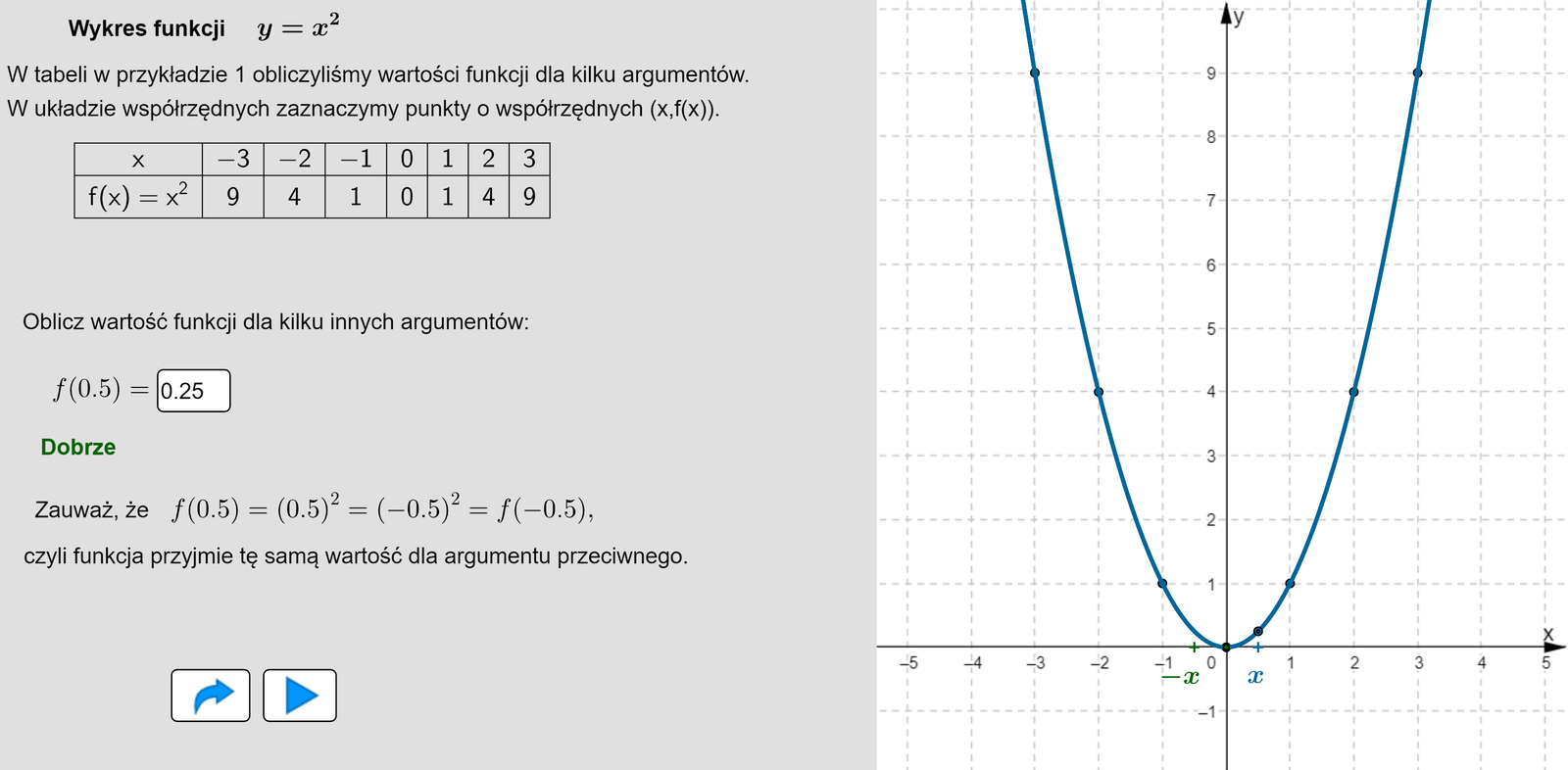
W poniższej tabeli zapisane są wartości funkcji dla kilku przykładowych argumentów.
Odczytujemy stąd, że . Uzasadnimy, że tylko dla tych dwóch argumentów funkcja przyjmuje wartość .
Argument , dla którego funkcja przyjmuje wartość , spełnia równanie , które jest równoważne równaniu
czyli
Otrzymany iloczyn jest równy wtedy i tylko wtedy, gdy jeden z jego czynników jest równy zero.
Wobec tego lub .
Stąd wtedy i tylko wtedy, gdy lub .
Zauważamy też, że i .
Wykażemy, że dla każdej pary argumentów, które są liczbami przeciwnymi, funkcja przyjmuje tę samą wartość.
Rozpatrzmy pewną liczbę , która jest różna od zera.
Wtedy oraz , co oznacza, że , czyli funkcja przyjmuje tę samą wartość dla takich dwóch argumentów, które są liczbami przeciwnymi.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PXROGE9iE
Z tabeli z Przykładu 1 odczytujemy, że , , , , więc .
Zauważmy też, że , , .
Uzasadnimy, że:
dla dowolnej nieujemnej liczby całkowitej prawdziwa jest nierówność ,
wraz ze wzrostem różnica rośnie.
Ad 1. Weźmy pewną liczbę całkowitą nieujemną . Wówczas i , więc , bo liczba jest nieujemna.
Ad 2. Ponieważ , więc wraz ze wzrostem rośnie wartość .
Pokażemy, że jedynym punktem wspólnym wykresu funkcji z osią jest punkt , a pozostałe punkty wykresu tej funkcji leżą powyżej osi .
Funkcja przyjmuje wyłącznie wartości nieujemne, ponieważ dla dowolnej liczby rzeczywistej jest .
Ponadto wtedy i tylko wtedy, gdy .
Zatem:
punkt jest jedynym punktem wspólnym wykresu funkcji z osią ,
pozostałe punkty wykresu tej funkcji leżą powyżej osi .
Uzasadnimy, że prosta określona równaniem jest osią symetrii wykresu funkcji .
Na wykresie funkcji możemy wskazać pary punktów symetrycznych względem osi . Np. oraz , a także i .
Jak wcześniej wykazaliśmy, funkcja przyjmuje tę samą wartość dla takich dwóch argumentów, które są liczbami przeciwnymi.
Zatem dla dowolnej liczby rzeczywistej zachodzi równość
, a to oznacza, że oś (czyli prosta o równaniu ) jest osią symetrii wykresu funkcji .
Uzasadniliśmy wcześniej, że dla dowolnej nieujemnej liczby całkowitej prawdziwa jest nierówność .
Wykażemy, że dla dowolnych liczb nieujemnych , , takich że , prawdziwa jest nierówność .
Weźmy takie dwie liczby nieujemne , , że . Wtedy
W otrzymanym iloczynie oba czynniki są dodatnie: , bo , natomiast , gdyż jest sumą liczby nieujemnej i liczby dodatniej .
Stąd , czyli .
Zatem (z uwagi na symetrię wykresu funkcji względem osi ).
maksymalny przedział, w którym funkcja jest rosnąca to ,
maksymalny przedział, w którym funkcja jest malejąca to .
Uzasadniliśmy wcześniej, że dla każdej pary argumentów, które są liczbami przeciwnymi, funkcja przyjmuje tę samą wartość.
Wykażemy, że dla każdej dodatniej liczby k istnieją dokładnie dwa takie argumenty funkcji , że .
Przekształcamy równanie
Ta równość zachodzi wtedy i tylko wtedy, gdy lub .
Zatem wtedy i tylko wtedy, gdy lub .
Liczby te są różne, gdyż .
To oznacza, że dowolna dodatnia liczba należy do zbioru wartości funkcji .
Ponieważ , to możemy stwierdzić, że zbiorem wartości funkcji jest przedział .
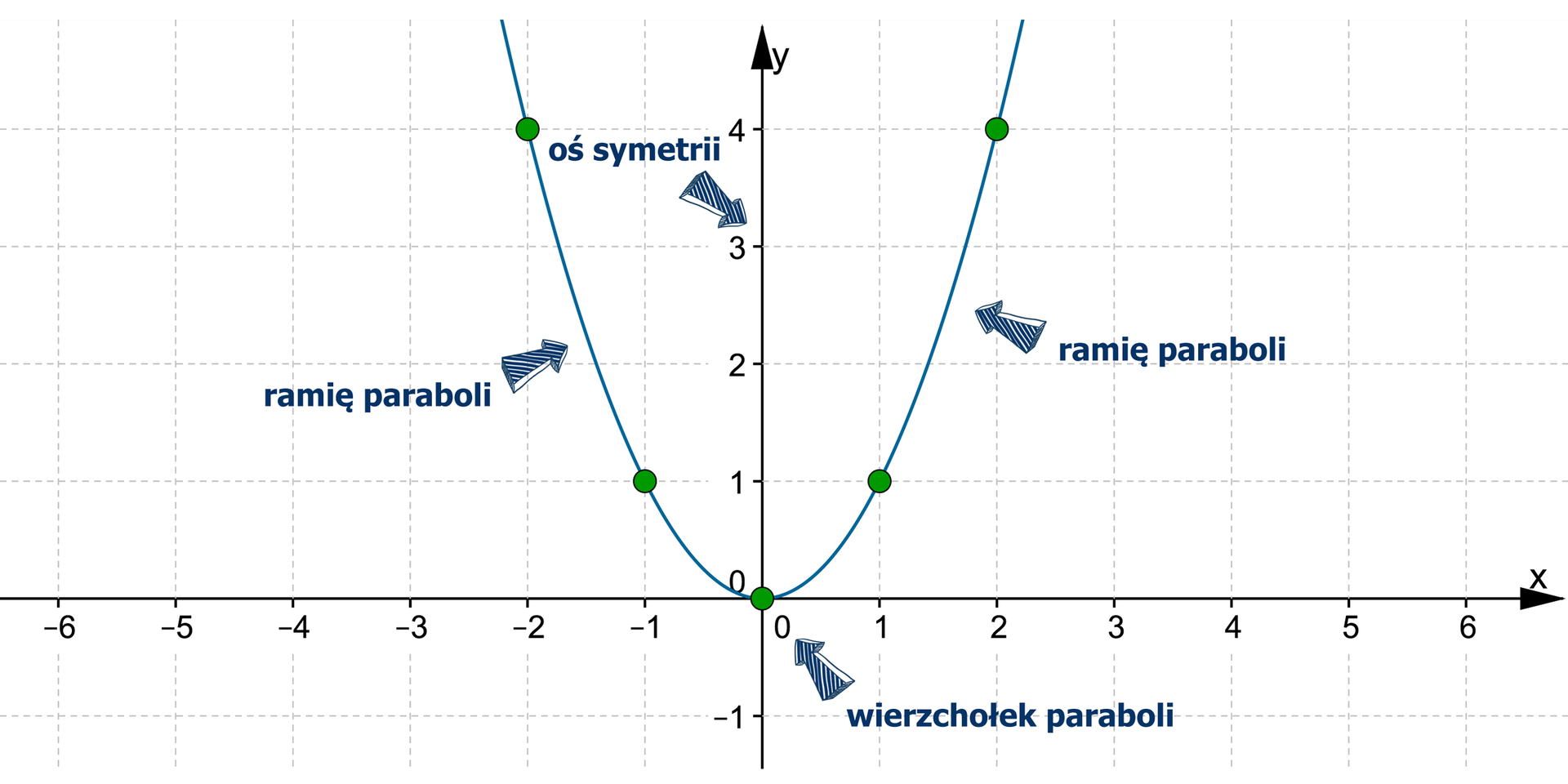
Wykresem funkcji jest krzywa o równaniu , którą nazywamy parabolą.
Punkt nazywamy wierzchołkiem tej paraboli.
Prosta jest osią symetrii tej paraboli. Symetryczne względem tej prostej części paraboli nazywać będziemy jej ramionami.
Ramiona paraboli skierowane są zgodnie ze zwrotem osi (mówimy też, że ramiona tej paraboli skierowane są w górę).
Parabola ta posiada dokładnie dwa punkty wspólne z każdą prostą o równaniu , gdzie .
Narysujemy wykres funkcji .
Ustalimy najpierw zależność między wykresem funkcji , a wykresem funkcji .
Wartości tych funkcji dla kilku przykładowych argumentów prezentuje poniższa tabela.
Zauważmy, że .
Dla ustalonego argumentu , oraz równość
co oznacza, że wartość funkcji jest dwa razy większa od wartości funkcji .
Wykres funkcji (krzywa o równaniu ) jest parabolą, której wierzchołkiem jest punkt , a ramiona skierowane są w górę.

W odniesieniu do wykresu funkcji rozpatrzmy wykres funkcji danej wzorem , gdzie jest ustaloną liczbą dodatnią.
Niezależnie od wartości jest .
Dla ustalonego niezerowego zachodzi równość .
Wykresem każdej takiej funkcji jest parabola, której wierzchołkiem jest punkt i ramiona skierowane są w górę.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PXROGE9iE
Krzywą o równaniu nazwaliśmy parabolą. Wykazaliśmy, że pewne jej własności ma również każda krzywa o równaniu , gdzie i na tej podstawie uznaliśmy, że każdą z tych krzywych można również nazwać parabolą.
Wybierzmy na płaszczyźnie dowolną prostą oraz punkt , który nie należy do tej prostej. Parabola to zbiór wszystkich punktów tej płaszczyzny, których odległość od prostej , zwanej kierownicą paraboli, jest równa odległości od punktu , tzw. ogniska paraboli.
Punkt paraboli, którego odległość od ogniska jest najmniejsza z możliwych, nazywamy wierzchołkiem paraboli. Wierzchołek leży w połowie odległości ogniska od kierownicy .
Prosta prostopadła do kierownicy i przechodząca przez ognisko jest osią symetrii paraboli i przecina tę parabolę w jej wierzchołku.
Wykażemy, że krzywa o równaniu to parabola, której kierownicą jest prosta o równaniu , a ogniskiem punkt .
Spośród punktów danej krzywej, najbliżej prostej leży punkt , jedyny punkt tej krzywej, który leży na osi .
Jego odległość zarówno od punktu , jak i od prostej jest równa .
Na krzywej o równaniu leżą też np. punkty i .
Pokażemy, że każdy z nich jest równo odległy od kierownicy i ogniska .
Dla punktu odległość od kierownicy jest równa , a odległość od ogniska jest równa
czyli również .
Dla punktu odległość od kierownicy jest równa , a odległość od ogniska jest równa
zatem i te dwie odległości są równe.
Pokażemy, że każdy punkt krzywej o równaniu leży w tej samej odległości od prostej i punktu .
Zauważmy, że dla dowolnej liczby rzeczywistej punkt leży na tej krzywej.
Odległość punktu od prostej to , a odległość punktu od ogniska jest równa
Zatem dla każdego odległości te są równe, więc krzywa o równaniu to parabola, której wierzchołkiem jest punkt , a jej osią symetrii jest prosta o równaniu .
Każda krzywa o równaniu , gdzie to parabola, której kierownicą jest prosta o równaniu , a ogniskiem jest punkt .
Dla dowolnej liczby rzeczywistej punkt leży na tej krzywej. Odległość punktu od prostej to , a odległość punktu od ogniska wyraża się wzorem
Odległości te są równe, zatem krzywa o równaniu to parabola. Jej wierzchołkiem jest punkt , a osią symetrii – prosta o równaniu .
Przesunięcie wykresu jednomianu kwadratowego wzdłuż osi układu współrzędnych
Narysujemy wykresy funkcji oraz .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PXROGE9iE
Rozpatrzmy parabolę o równaniu .
Zauważmy, że:
po jej przesunięciu o jednostki w dół wzdłuż osi otrzymamy parabolę o równaniu . Wykresem funkcji jest więc parabola, której wierzchołek to , a jej ramiona skierowane są w górę. Prosta jest osią symetrii tej paraboli. Zatem maksymalny przedział, w którym funkcja jest rosnąca, to , a maksymalny przedział, w którym funkcja jest malejąca, to . Zbiór wartości funkcji to .
RtNkBbxpipSmW1 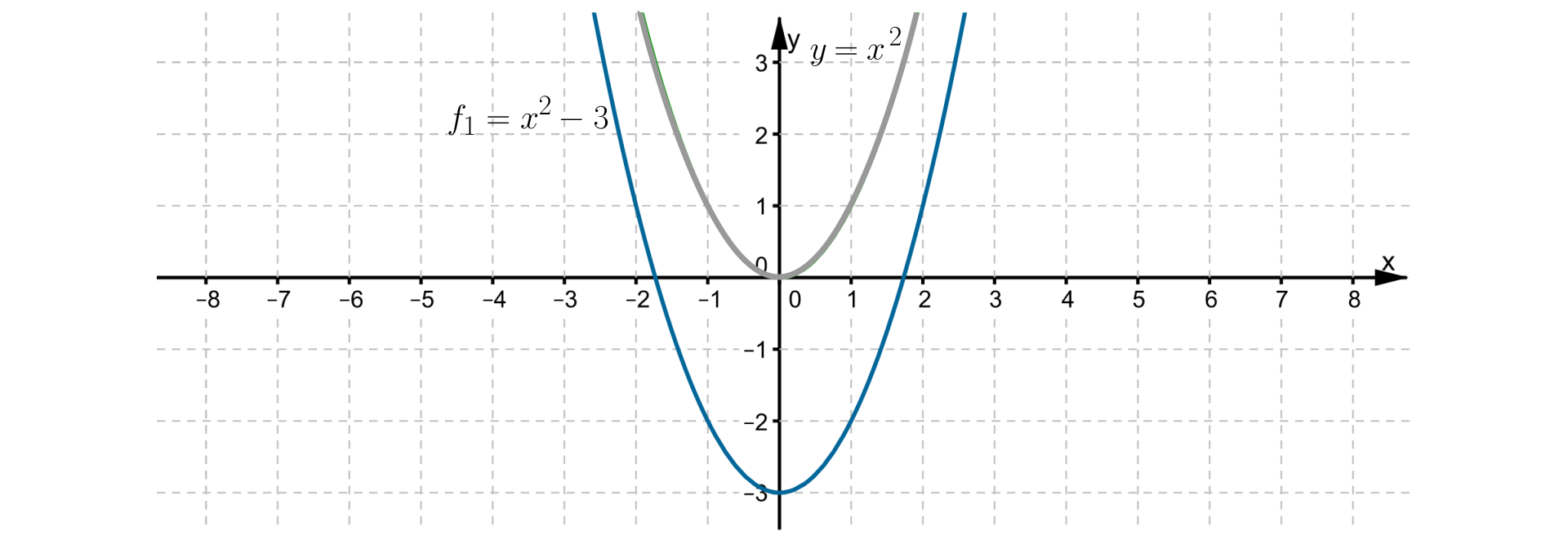 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
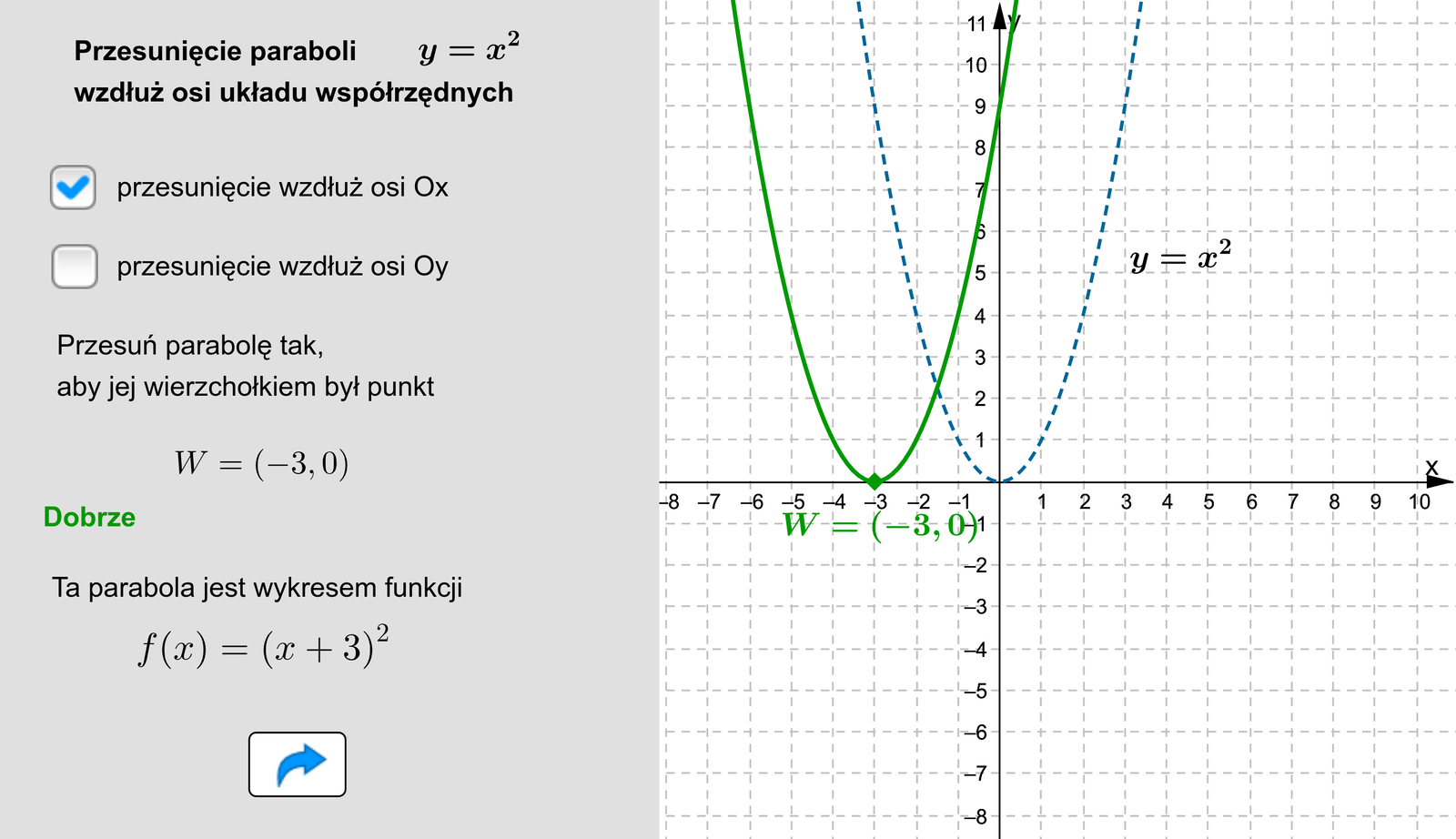
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.po jej przesunięciu o jednostki w prawo wzdłuż osi otrzymamy parabolę o równaniu . Stąd wykresem funkcji jest parabola o wierzchołku w punkcie , której ramiona skierowane są w górę. Prosta jest osią symetrii tej paraboli. Wobec tego przedział to maksymalny przedział, w którym funkcja jest rosnąca, a przedział to maksymalny przedział, w którym funkcja jest malejąca. Zbiór wartości funkcji to .
RF516yxFOmTuN1 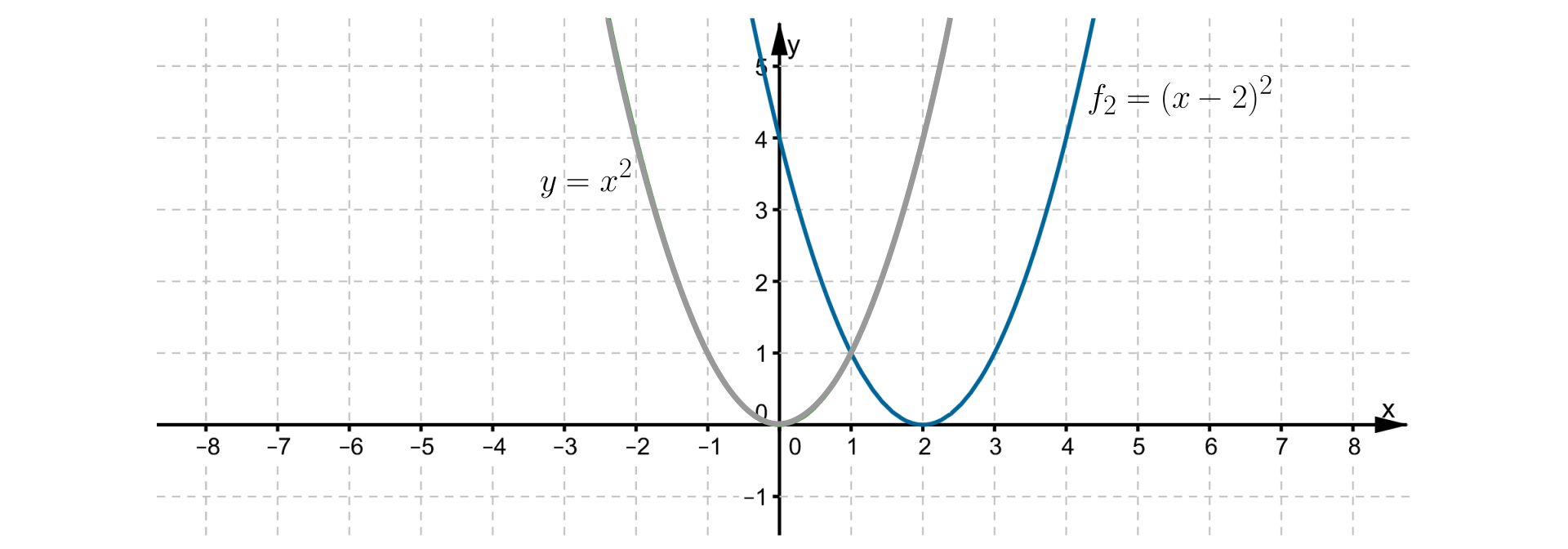 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Narysujemy wykresy funkcji.
,
,
,
.
Rozpatrzmy funkcję daną wzorem , gdzie jest ustaloną liczbą różną od zera.
Obrazem wykresu funkcji w przesunięciu o jednostek wzdłuż osi jest wykres takiej funkcji , że . Jest to więc parabola przystająca do paraboli o równaniu , której wierzchołkiem jest punkt . Osią symetrii tej paraboli jest prosta o równaniu .
Obrazem wykresu funkcji w przesunięciu o jednostek wzdłuż osi jest wykres takiej funkcji , że . Jest to więc parabola przystająca do paraboli o równaniu , której wierzchołkiem jest punkt . Osią symetrii tej paraboli jest prosta o równaniu .
Wobec powyższego:
Wykresem funkcji jest parabola, której wierzchołkiem jest punkt , a jej ramiona są skierowane w górę. Osią symetrii tej paraboli jest prosta o równaniu . Maksymalny przedział, w którym funkcja jest rosnąca, to , a maksymalny przedział, w którym funkcja jest malejąca, to . Zbiór wartości funkcji to .
R1AE857RKXn9y1 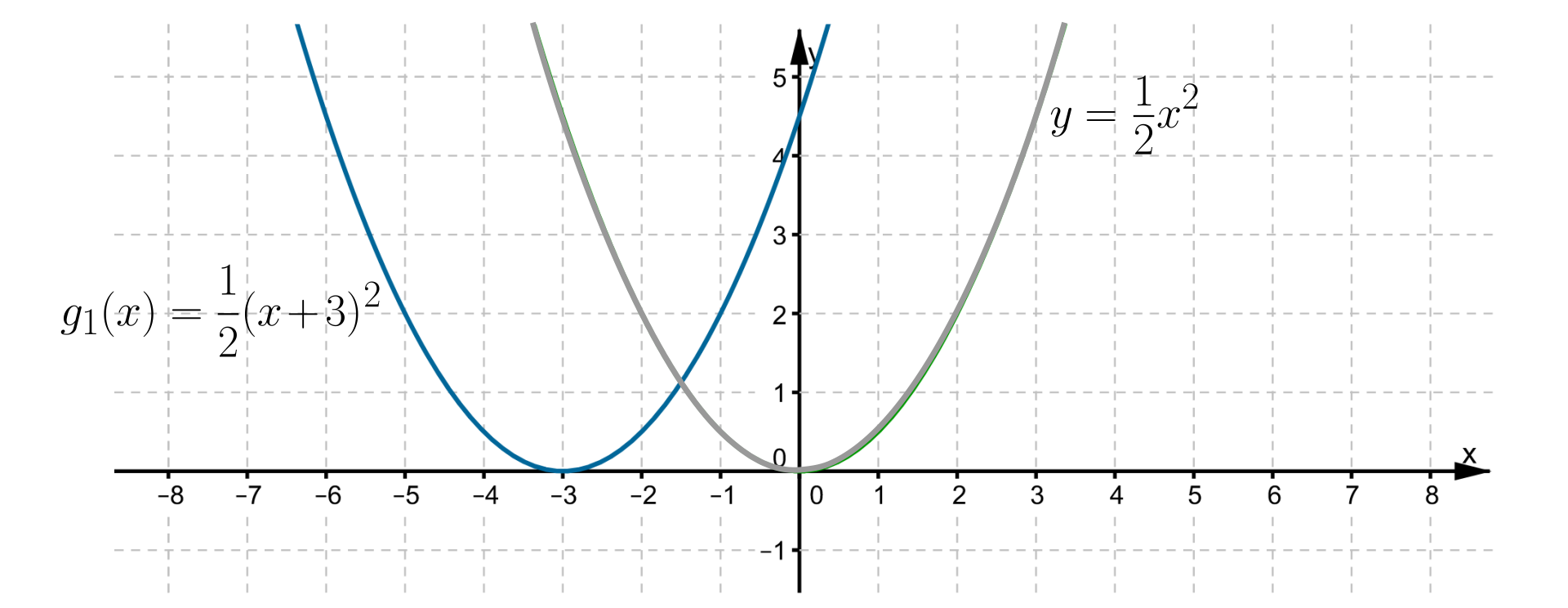 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wykresem funkcji jest parabola, której wierzchołkiem jest punkt , a jej ramiona skierowane są w górę. Osią symetrii tej paraboli jest prosta o równaniu . Maksymalny przedział, w którym funkcja jest rosnąca, to , a maksymalny przedział, w którym jest ona malejąca, to . Zbiór wartości funkcji to .
RXKOvmI3tJjCv1 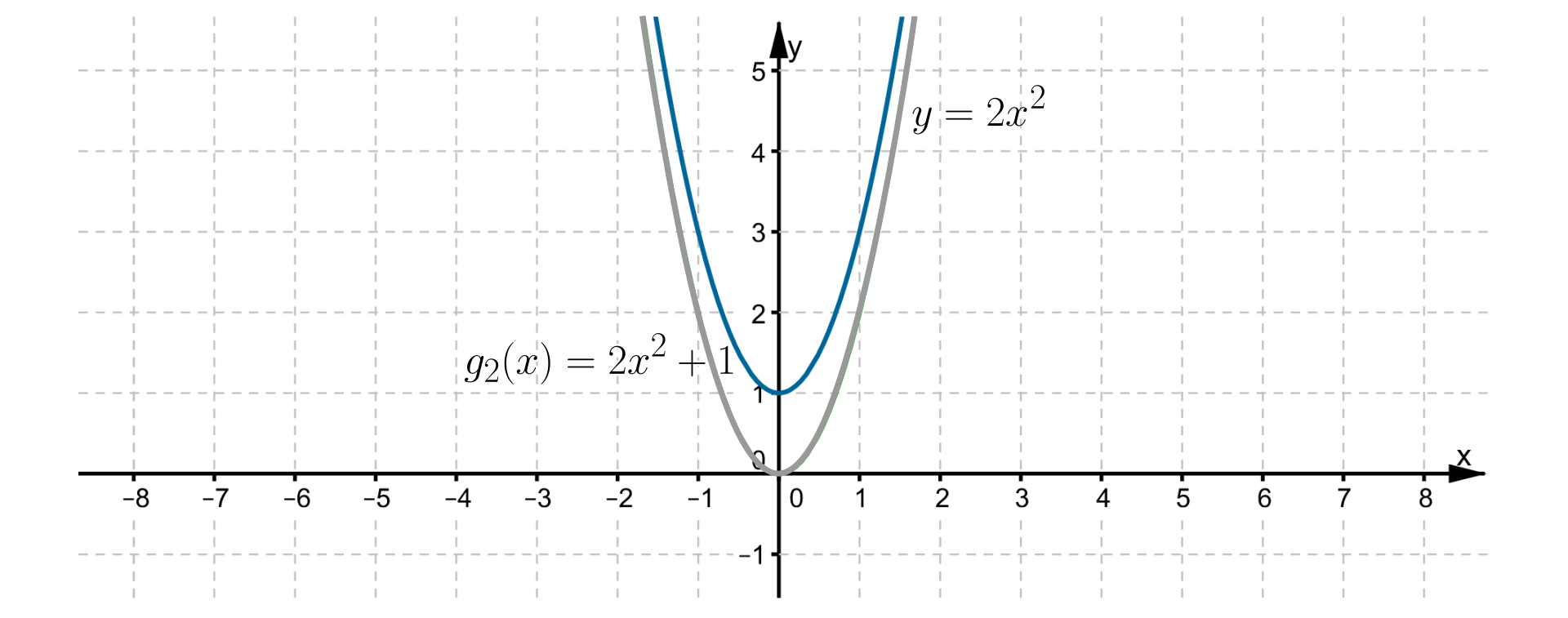 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wykresem funkcji jest parabola, której wierzchołkiem jest punkt , a jej ramiona są skierowane w dół. Osią symetrii tej paraboli jest prosta o równaniu . Maksymalny przedział, w którym funkcja jest rosnąca, to , a maksymalny przedział, w którym jest ona malejąca, to . Zbiór wartości funkcji to .
RA6dB5zem747m1 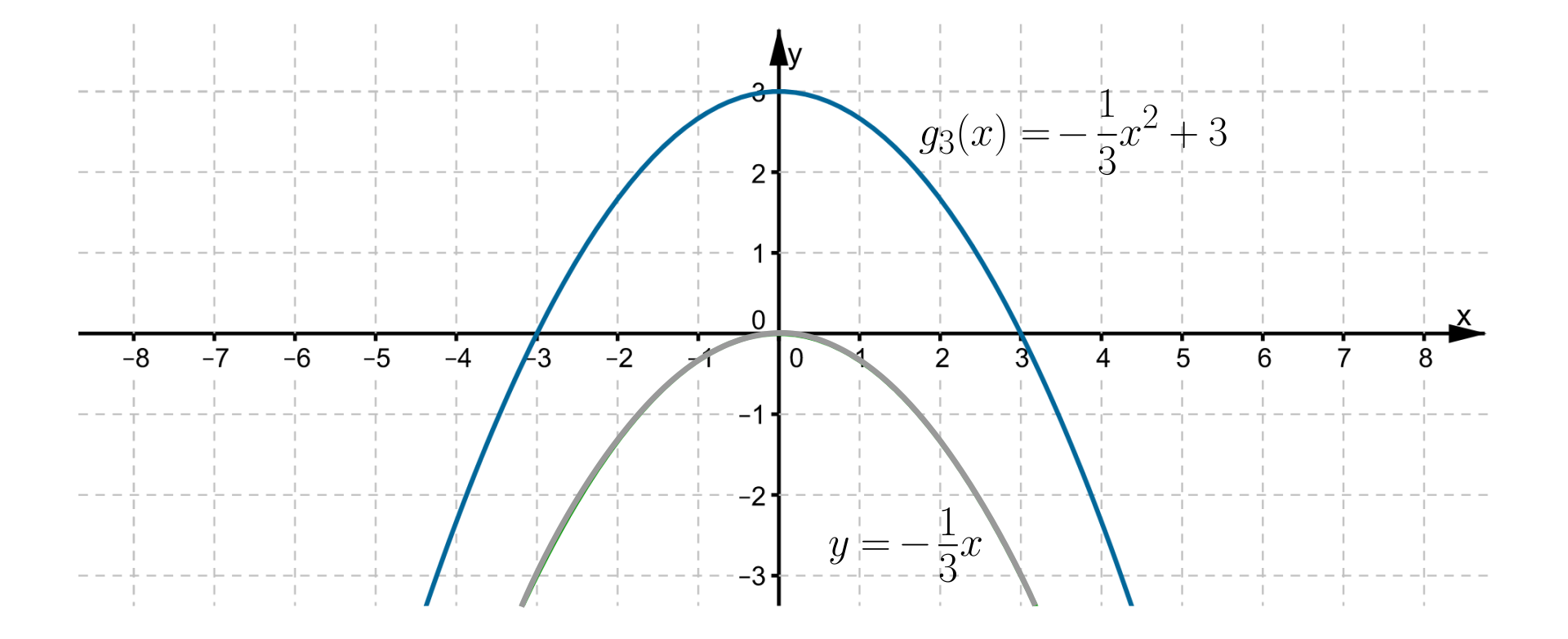 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wykresem funkcji jest parabola, której wierzchołkiem jest punkt , a jej ramiona są skierowane w dół. Osią symetrii tej paraboli jest prosta o równaniu . Maksymalny przedział, w którym funkcja jest rosnąca, to , a maksymalny przedział, w którym jest ona malejąca, to . Zbiór wartości funkcji to .
RUl47UxXFIMjV1 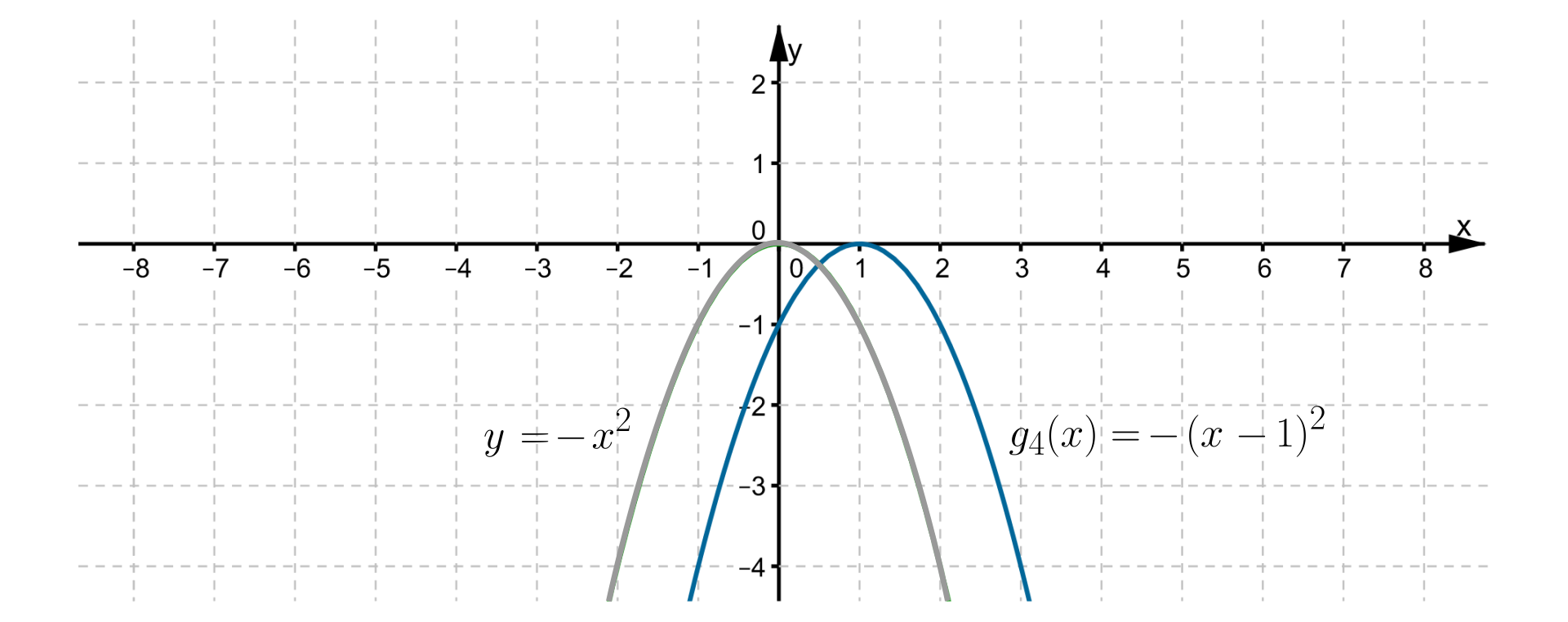 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Znajdziemy równania parabol, które są zaprezentowane na poniższych rysunkach.
R1DvHQM9TzVPX1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Rgk5T4gsfeleo1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R7uum6y7aCPJV1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RGI42iKpgPpxS1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ad 1. Wierzchołkiem paraboli jest punkt , więc ma ona równanie postaci . Na tej paraboli leży też punkt , zatem , stąd . Wobec tego równanie tej paraboli to .
Ad 2. Wierzchołkiem paraboli jest punkt , zatem ma ona równanie postaci . Na tej paraboli leży też punkt , więc , stąd . To znaczy, że ta parabola ma równanie .
Ad 3. Wierzchołkiem paraboli jest punkt , więc ma ona równanie postaci . Na tej paraboli leży też punkt , zatem , stąd . To znaczy, że ta parabola ma równanie .
Ad 4. Wierzchołkiem paraboli jest punkt , zatem ma ona równanie postaci . Na tej paraboli leży też punkt , więc , stąd . Wobec tego równanie tej paraboli to .
- przesunąć parabolę o równaniu o jednostki wzdłuż osi
- przesunąć parabolę o równaniu o jednostki wzdłuż osi
- odbić parabolę o równaniu symetrycznie względem osi
- odbić parabolę o równaniu symetrycznie względem osi
Na rysunku przedstawiono parabolę, która jest wykresem funkcji .

Na rysunku przedstawiono parabolę, która jest wykresem funkcji .

Uzupełnij luki na rysunkach. Wpisz brakujące części wzorów reprezentujących parabole, na przykład „”. Uzupełnij współrzędne wierzchołka każdej paraboli, na przykład „”. Uzupełnij również równanie osi symetrii w każdym przypadku.
Uzupełnij luki na ilustracjach. Określ znak przed , wpisując „” albo „”. Wpisz brakujące części wzorów reprezentujących parabole, na przykład „”. Uzupełnij współrzędne wierzchołka każdej paraboli, na przykład „”. Uzupełnij również równanie osi symetrii w każdym przypadku.
Rozpatrzmy funkcję . Wykaż, że dla dowolnej liczby całkowitej różnica jest liczbą nieparzystą.



