Liczby całkowite - zebranie wiadomości

RzlZiFYvG4FQG

R1DG51CtBQ1Cb1

Obraz "Lichwiarze" autorem jest Quentin Massys. Przedstawia czterech mężczyzn z grymasami na twarzach, którzy pochyleni są nad książką i monetami. — Źródło: *Quentin Massys, Lichwiarze*, dostępny w internecie: Wikipedia.org, domena publiczna.

Koncepcja liczb ujemnych powstała w $I$ wieku p. n. e w Chinach.

W $VII$ wieku liczby ujemne stosowano w Indiach do księgowania długów. W Europie liczby ujemne również wykorzystywano przy operacjach finansowych, jednak aż do $XVIII$ wieku nie uznawano powszechnie tych liczb i odrzucano ujemne rozwiązania równań.

Obecnie nikogo nie dziwi wzmianka o liczbach ujemnych. Spotykamy się bowiem z nimi niemal codziennie – odczytując temperaturę powietrza, wzrost lub spadek kursów walut, określając poziomy pięter budynków.

W tym materiale znajdziesz najważniejsze informacje o liczbach całkowitych, a w szczególności o liczbach całkowitych ujemnych.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Gra edukacyjnaGra edukacyjna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Rozpoznasz liczby dodatnie i ujemne.
Podasz przykłady zastosowania liczb ujemnych w życiu codziennym.
Podasz liczbę przeciwną do danej liczby całkowitej.
Określisz wartość bezwzględną danej liczby całkowitej.
Przedstawisz liczbę całkowitą na osi liczbowej.
Porównasz liczby całkowite.
Obliczysz wartość liczbową wyrażenia zwierającego liczby ujemne.

R1JNNnHZPgSu1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Na wykresie przedstawiono, jak zmieniała się temperatura powietrza w miejscowości Jedlicze w pierwszym tygodniu listopada, notowana codziennie o godz. $13:30$ .

R1a50giMs6T99

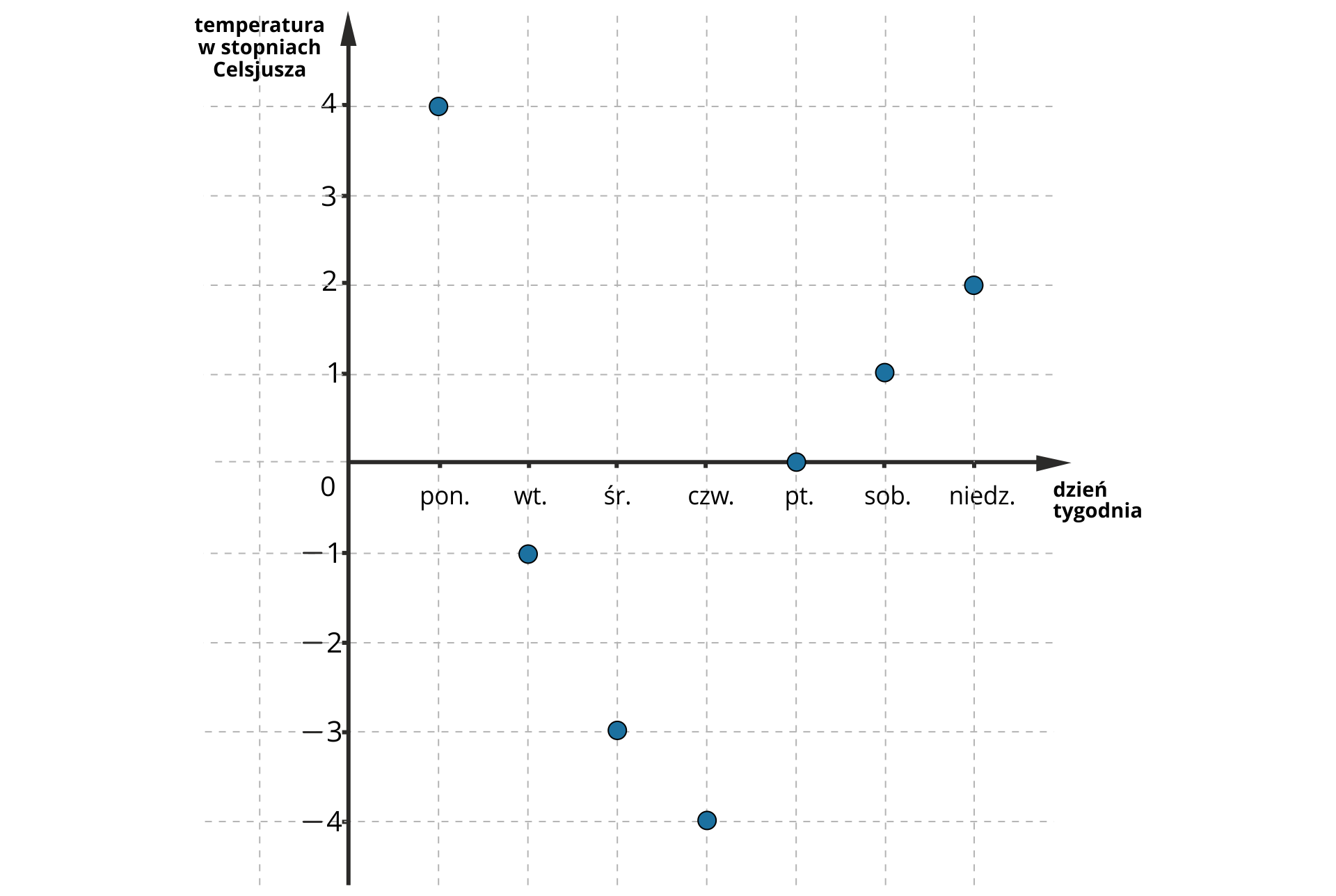
Na ekranie ukazany kartezjański układ współrzędnych. Oś pozioma ma zwrot w prawą stronę. Zaznaczone są na niej dni tygodnia. Poniedziałek, wtorek, środa, czwartek, piątek, sobota, niedziela. Oś pionowa ma zwrot w górę. Podpisana jest w następujący sposób: "Temperatura w stopniach Celsjusza". Na osi znajdują się wartości od -4 do 4, rosnące co jeden. Na wykresie zaznaczono za pomocą niebieskich kółek następujące wartości. Poniedziałek 4 stopnie, wtorek -1, środa -3, czwartek -4, piątek 0, sobota 1, niedziela 2. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Na podstawie wykresu można stwierdzić, że w poniedziałek, sobotę i niedzielę, zanotowano temperatury powyżej zera. Natomiast we wtorek, środę i czwartek zanotowano temperatury poniżej zera.

Liczby wyrażające temperaturę powietrza w poniedziałek, sobotę i niedzielę to liczby dodatnie.
Liczby wyrażające temperaturę powietrza we wtorek, środę i czwartek to liczby ujemne.
Liczba zero, wyrażająca temperaturę powietrza w piątek, nie jest ani dodatnia, ani ujemna.
Liczbę ujemną oznaczamy znakiem minus.

Przykład 1

Przykłady liczb ujemnych
Piszemy	Czytamy
$- 1$	minus jeden
$- 4$	minus cztery
$- 7$	minus siedem
$- 10$	minus dziesięć
$- 26$	minus dwadzieścia sześć
$- 138$	minus sto trzydzieści osiem

Ważne!

Liczby $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $\dots$ , $\dots$ to liczby całkowiteliczby całkowiteliczby całkowite dodatnie.
Liczby $- 1$ , $- 2$ , $- 3$ , $- 4$ , $\dots$ , $\dots$ to liczby całkowiteliczby całkowiteliczby całkowite ujemne.
Liczba $0$ nie jest liczbą dodatnią, ani ujemną.
Liczby $0$ , $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $\dots$ , $\dots$ to liczby całkowiteliczby całkowiteliczby całkowite nieujemne.
Liczby $0$ , $- 1$ , $- 2$ , $- 3$ , $- 4$ , $\dots$ , $\dots$ to liczby całkowiteliczby całkowiteliczby całkowite niedodatnie.

Liczby dodatnie na osi liczbowej położone są na prawo od zera, a liczby ujemne na lewo.

R4x9s1v36gurl

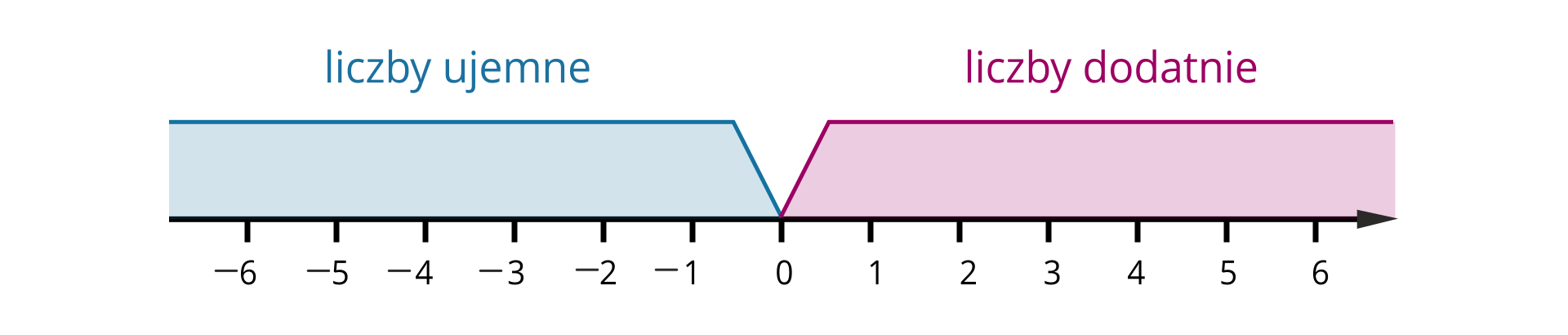
Oś pozioma ze zwrotem w prawo. Zaznaczone są na niej wartości od -6 do 6, rosnące co 1. Obszar od zera w lewą stronę zaznaczono kolorem niebieskim i podpisano jako liczby ujemne. Obszar od zera w prawą stronę zaznaczono kolorem różowym i podpisano jako liczby dodatnie. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 2

Zaznaczymy na osi liczbowej $- 5$ , $- 2$ , $2$ , $5$ .

RE7BxMVo6aeLi

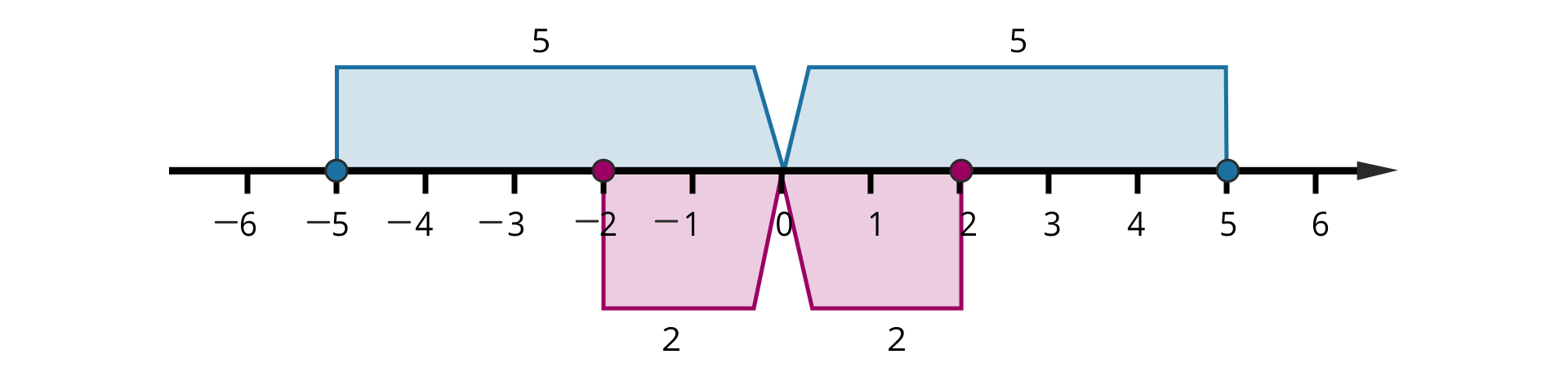
Oś pozioma ze zwrotem w prawo. Zaznaczone są na niej wartości od -6 do 6, rosnące co 1. Zaznaczono na niej cztery przedziały. Przedział pierwszy zaznaczony kolorem niebieskim obejmuje obszar od zera do pięciu. Nad przedziałem zapisana jest liczba 5. Przedział drugi zaznaczony kolorem niebieskim obejmuje obszar od zera do minus pięciu. Nad przedziałem zapisana jest liczba 5. Przedział trzeci zaznaczony kolorem różowym obejmuje obszar od zera do dwóch. Nad przedziałem zapisana jest liczba 2. Przedział czwarty zaznaczony kolorem różowym obejmuje obszar od zera do minus dwóch. Nad przedziałem zapisana jest liczba 2. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zauważmy, że liczby $- 2$ i $2$ leżą na osi liczbowej po przeciwnych stronach zera w równych odległościach od zera. Podobnie liczby $- 5$ i $5$ leżą na osi liczbowej po przeciwnych stronach zera w równych odległościach od zera.
Takie liczby nazywamy przeciwnymi.

Przykład 3

Przykłady liczb przeciwnych.

$- 4$ i $4$
$10$ i $- 10$
$- 127$ i $127$
$567$ i $- 567$

Ważne!

Liczby całkowiteliczby całkowiteLiczby całkowite to liczby naturalne dodatnie, liczby do nich przeciwne i liczba zero.

Odległość liczby od zera na osi liczbowej nazywamy wartością bezwzględną tej liczby.

Na przykład odległość liczby $6$ od zera jest równa $6$ . Zapisujemy:

|6| = 6

Przykład 4

Określimy wartość bezwzględnąwartość bezwzględnawartość bezwzględną każdej z liczb: $5$ , $0$ , $- 7$ , $- 11$ .

|5| = 5

|0| = 0

|- 7| = 7

|- 11| = 11

Liczby przeciwneliczby przeciwneLiczby przeciwne leżą w tej samej odległości od zera na osi liczbowej. Zatem ich wartości bezwzględne są równe.
Na przykład:
$|- 1| = 1$ i $|1| = 1$
$|- 79| = 79$ i $|79| = 79$

Analizując położenie na osi liczbowej liczb dodatnich i ujemnych, zauważamy, że każda liczba dodatnia jest większa od każdej liczby ujemnej i zera.
Z dwóch liczb ujemnych ta jest większa, której wartość bezwzględnawartość bezwzględnawartość bezwzględna jest mniejsza.

Przykład 5

Zapiszemy liczby: $9$ , $- 1$ , $7$ , $0$ , $- 2$ , $4$ , $- 6$ , $- 11$ od najmniejszej do największej.

- 11 < - 6 < - 2 < - 1 < 0 < 4 < 7 < 9

Aby dodać dwie liczby całkowiteliczby całkowiteliczby całkowite ujemne, dodajemy ich wartości bezwzględne i przed wynikiem stawiamy znak minus. Aby dodać dwie liczby całkowiteliczby całkowiteliczby całkowite różnych znaków, odejmujemy od większej wartości bezwzględnej, mniejszą wartość bezwzględną, a przed wynikiem stawiamy znak, jaki ma liczba o większej wartości bezwzględnej.

Przykład 6

Wykonamy dodawanie.

- 1 + (- 2) = - 3

- 8 + (- 4) = - 12

$- 4 + 6 = 6 - 4 = 2$ , bo $|6| > |- 4|$
$- 10 + 2 = - 8$ , bo $|- 10| > |2|$
$- 3 + 3 = 0$ , bo $|- 3| = |3|$

Odejmowanie liczby można zastąpić dodawaniem liczby przeciwnejliczby przeciwneliczby przeciwnej.
Na przykład:

- 8 - 4 = - 8 + (- 4) = - 12

7 - 10 = 7 + (- 10) = - 3

Aby pomnożyć (podzielić) liczby całkowiteliczby całkowiteliczby całkowite, różne od zera, należy pomnożyć (podzielić) ich wartości bezwzględne i przed wynikiem postawić znak

plus, jeżeli w iloczynie (ilorazie) występuje parzysta ilość liczb ujemnych,
minus, jeżeli w iloczynie (ilorazie) występuje nieparzysta ilość liczb ujemnych.

Przykład 7

Kolumna pierwsza	Kolumna druga
$- 2 \cdot (- 3) \cdot 10 = 60$	$- 10 : (- 2) = 5$
$5 \cdot (- 1) \cdot (- 3) \cdot (- 2) = - 30$	$- 4 : 2 = - 2$
$0 \cdot (- 2) = 0$	$0 : (- 2) = 0$
$(- 1) \cdot 6 \cdot (- 2) \cdot 3 = 36$	$- 12 : (- 2) : (- 3) = - 2$

Reguły dotyczące wykonywania działań na liczbach całkowitych są takie same, jak reguły wykonywania działań na liczbach naturalnych.

Przykład 8

Monika pożyczyła od Magdy $10 zł$ , od Karola $6 zł$ i od Wandy $12 zł$ . Od dziadka dostała $15 zł$ , a od mamy taką kwotę, że obie te kwoty łącznie wystarczyły jej na spłatę zaciągniętych długów. Obliczymy, jaką kwotę dostała Monika od mamy.

Obliczymy najpierw, ile jeszcze pieniędzy potrzebowała Monika, po otrzymaniu pieniędzy od dziadka.

15 - (10 + 6 + 12) = 15 - 28 = - 13

Monika potrzebowała jeszcze $13 zł$ , zatem mama dała jej właśnie taką kwotę.

Notatki

R1JFzwxi18dx2

Gra edukacyjna

Zagraj w grę. Zaznacz prawdziwe równości oraz prawdziwe nierówności.

RbXO0Lr1F7Vh4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Etap pierwszy:

R1XLgLJ4GEFM2

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Etap drugi:

R179gC1HSQIyv

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 1

Oblicz.

$- 6 : 3 + 4 \cdot 5 - (- 3) \cdot (- 6)$
$(- 7 - 8 - 9) - (- 24)$
$(- 3 + 7 + 3 - 7) \cdot 10$
$(10 - 9) (9 - 10)$

RhKeBXJJLvV4F

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$- 6 : 3 + 4 \cdot 5 - (- 3) \cdot (- 6) = - 2 + 20 - 18 = 18 - 18 = 0$
$(- 7 - 8 - 9) - (- 24) = - 24 + 24 = 0$
$(- 3 + 7 + 3 - 7) \cdot 10 = 0 \cdot 10 = 0$
$(10 - 9) (9 - 10) = 1 \cdot (- 1) = - 1$

Polecenie 2

Porównaj liczby.

$- 12$ i $10$
$- 8$ i $10$
$- 9$ i $- 12$
$0$ i $- 4$

RIw6DbL0MsH5a

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$- 12 < 10$
$- 8 < 10$
$- 9 > - 12$
$0 > - 4$

Polecenie 3

Oblicz iloczyn wszystkich liczb niedodatnich spośród liczb: $19$ , $(- 19)$ , $(- 5)$ , $0$ , $11$ , $14$ , $(- 24)$ .

RtopqkiMH5Knp

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Iloczyn liczby całkowitej i liczby $0$ jest równy $0$ .

$(- 19) \cdot (- 5) \cdot (- 24) \cdot 0 = 0$

Zestaw ćwiczeń interaktywnych

R17ReqWq0w3JR

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RH67RWxO6WY2Y

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RNwVKK5FIHRFN

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RIDvsHqvB5P2p

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R15MRcBbtDc2j

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RWNIIRvounZAF

Ćwiczenie 6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

Uporządkuj liczby: $4$ , $0$ , $(- 2)$ , $11$ , $(- 8)$ , $(- 3)$ , $(- 4)$ od najmniejszej do największej.

R1C5XZoa89L9P

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$- 8 < - 4 < - 3 < - 2 < 0 < 4 < 11$

Ćwiczenie 8

Sumę liczb $(- 6)$ i $(- 9)$ pomnóż przez różnicę tych liczb i wynik podziel przez $(- 5)$ .

RA7k6tamqxq7A

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$\frac{[- 6 + (- 9)] [- 6 - (- 9)]}{- 5} = \frac{(- 6 - 9) (- 6 + 9)}{- 5} = \frac{- 15 \cdot 3}{- 5} = \frac{- 45}{- 5} = 9$

Ćwiczenie 9

Dzisiaj rano temperatura powietrza w Krakowie wynosiła $- 10 ° C$ . W Warszawie była o $4 ° C$ wyższa niż w Krakowie. W Poznaniu temperatura powietrza była o $7 ° C$ niższa niż w Warszawie.

W którym z miast – Poznaniu czy Krakowie temperatura powietrza była wyższa i o ile stopni Celsjusza?

RQkusA7VLsTIE

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Obliczamy temperaturę powietrza w każdym z miast.

Kraków: $- 10 ° C$
Warszawa: $- 10 ° C + 4 ° C = - 6 ° C$
Poznań: $- 6 ° C - 7 ° C = - 13 ° C$

Obliczamy różnicę temperatur.

|- 13| - |- 10| = 3

Temperatura powietrza była w Poznaniu niższa niż w Krakowie o $3 ° C$ .

Słownik

liczby całkowite

to liczby naturalne dodatnie, liczby do nich przeciwne i liczba zero.

wartość bezwzględna

odległość liczby od zera na osi liczbowej.

liczby przeciwne

różne liczby, które mają takąość bezwzględną.

Bibliografia

Stewart I., (2020), Po co nam matematyka, Warszawa: Prószyński i S‑ka.