Mnożenie dwumianu przez dwumian

Strażnikiem wrót prowadzących do pewnej piramidy jest sfinks. Jeśli chcesz wejść do piramidy, musisz rozwiązać zagadkę, którą zada ci sfinks. W przeciwnym razie może zamienić cię w kamień.
Zagadka sfinksa.
Suma dwóch liczb jest równa siedem, a ich różnica jest równa trzynaście. Ile jest równa różnica kwadratów tych liczb?
Czy potrafisz rozwiązać zagadkę sfinksa?
Jeśli nie – zapoznaj się z poniższym materiałem, a znajdziesz tam odpowiedź. Jeśli zagadka została przez Ciebie rozwiązana – również zajrzyj do poniższego materiału, aby rozszerzyć swoje umiejętności.
Bowiem w tym materiale zajmiemy się mnożeniem dwumianów, czy wyrażeń algebraicznych, będących sumą dwóch jednomianów.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Ilustracja interaktywnaIlustracja interaktywna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Pomnożysz dwa dwumiany.
Zapiszesz w prostszej postaci wyrażenie wymagające mnożenia dwumianów.
Wykorzystasz interpretację geometryczną wyrażeń algebraicznych w obliczeniach.
Prostokąt przedstawiony na rysunku podzielono na mniejsze prostokąty.
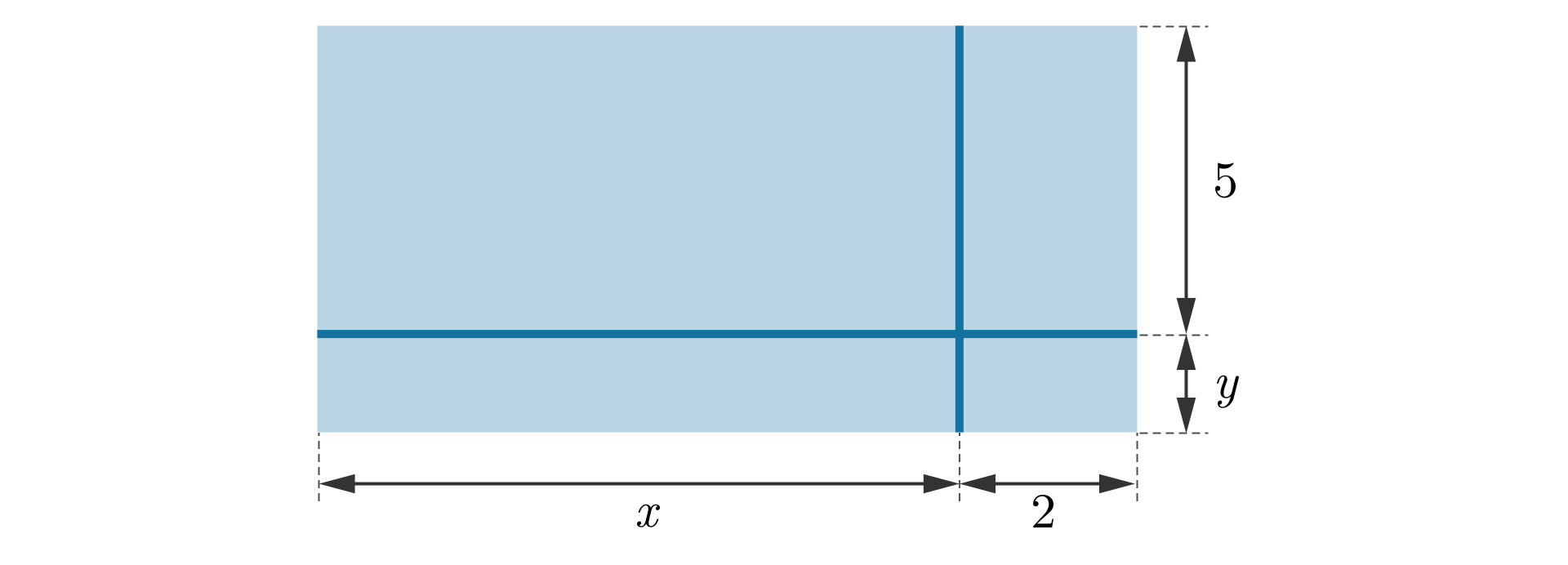
Pole tego prostokąta opisują wyrażenia oraz .
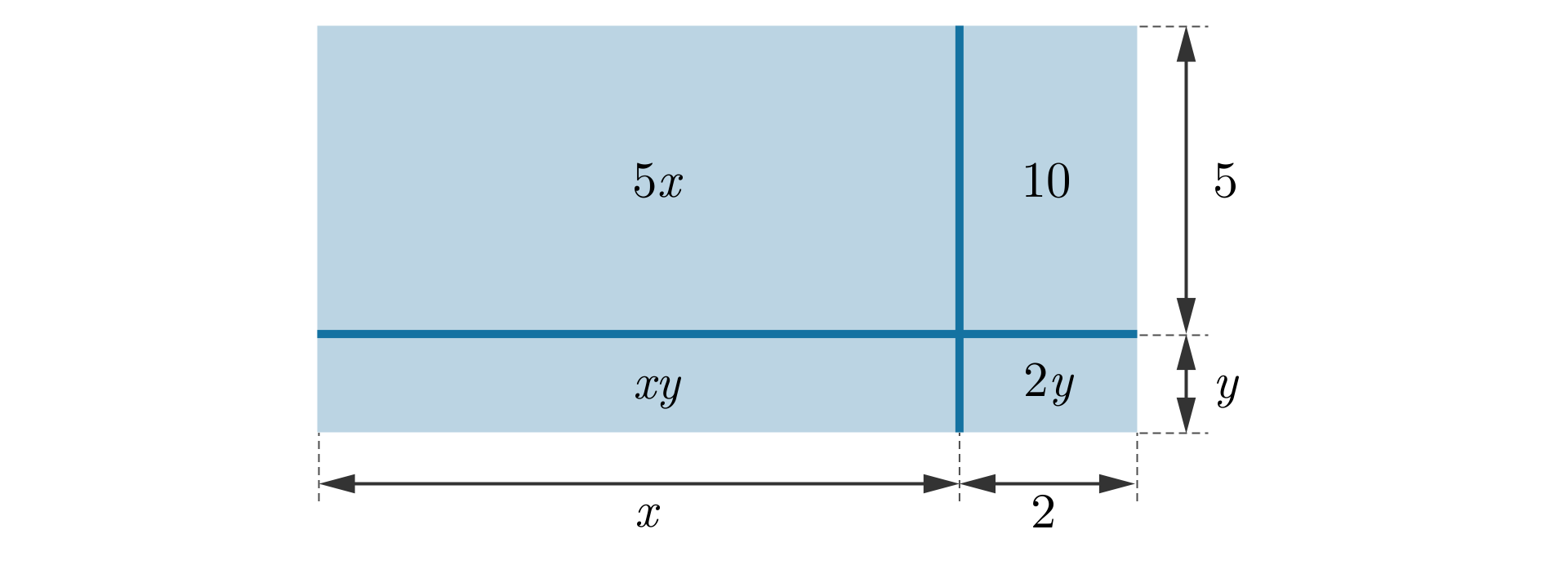
Możemy więc zapisać:
Zatem wyrażenie zapisane po prawej stronie równości otrzymujmy, mnożąc sumy algebraicznemnożąc sumy algebraiczne i .
Chcąc w inny sposób wykonać to mnożenie, stosujemy prawo rozdzielności mnożenia względem dodawania.
Wykonać mnożenie możemy też w prostszej wersji – mnożąc od razu każdy wyraz pierwszego dwumianu, przez każdy wyraz drugiego dwumianu.
Korzystając z powyższego przykładu, podamy sposób mnożenia sum algebraicznychmnożenia sum algebraicznych.
Aby pomnożyć dwie sumy algebraiczne, należy każdy wyraz pierwszej sumy pomnożyć przez każdy wyraz drugiej sumy i otrzymane jednomiany dodać.
Zapiszemy iloczyn w postaci sumy.
Mnożenie | Obliczenia pomocnicze |
|---|---|
Mnożenie sum algebraicznych wykorzystamy do zapisania kwadratu dwumianu w postaci sumy.
Zapiszemy wyrażenie w postaci sumy.
Aby wykonać potęgowanie, zapisujemy kwadrat danego wyrażenia w postaci iloczynu, a następnie mnożymy.
Redukujemy wyrazy podobne.
Mnożenie dwumianów czasem wykonujemy sposobem pisemnym, podobnie jak mnożymy liczby naturalne.
Pomnożymy pisemnie i .
Krok
Zapisujemy jeden dwumian pod drugim.
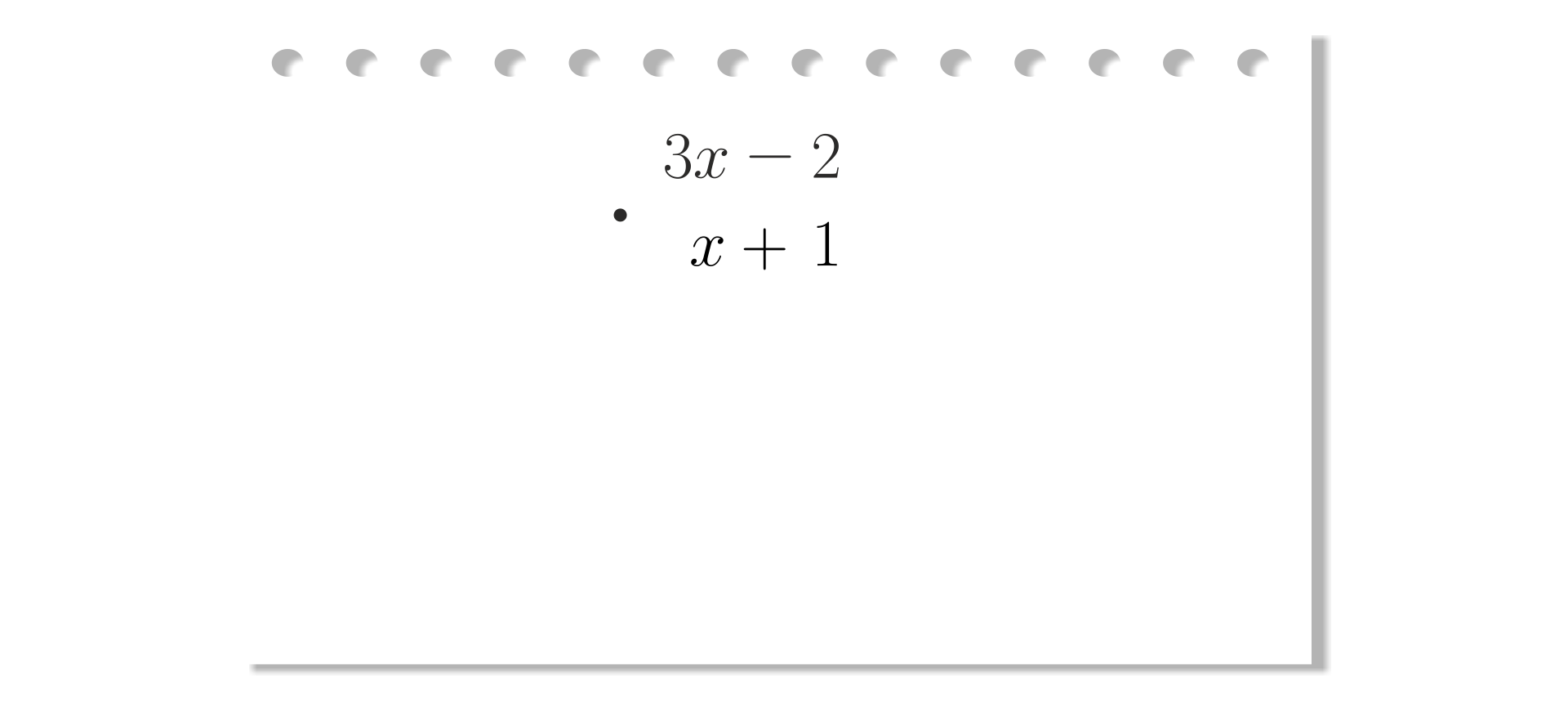
Krok
Mnożymy pierwszy dwumian przez .
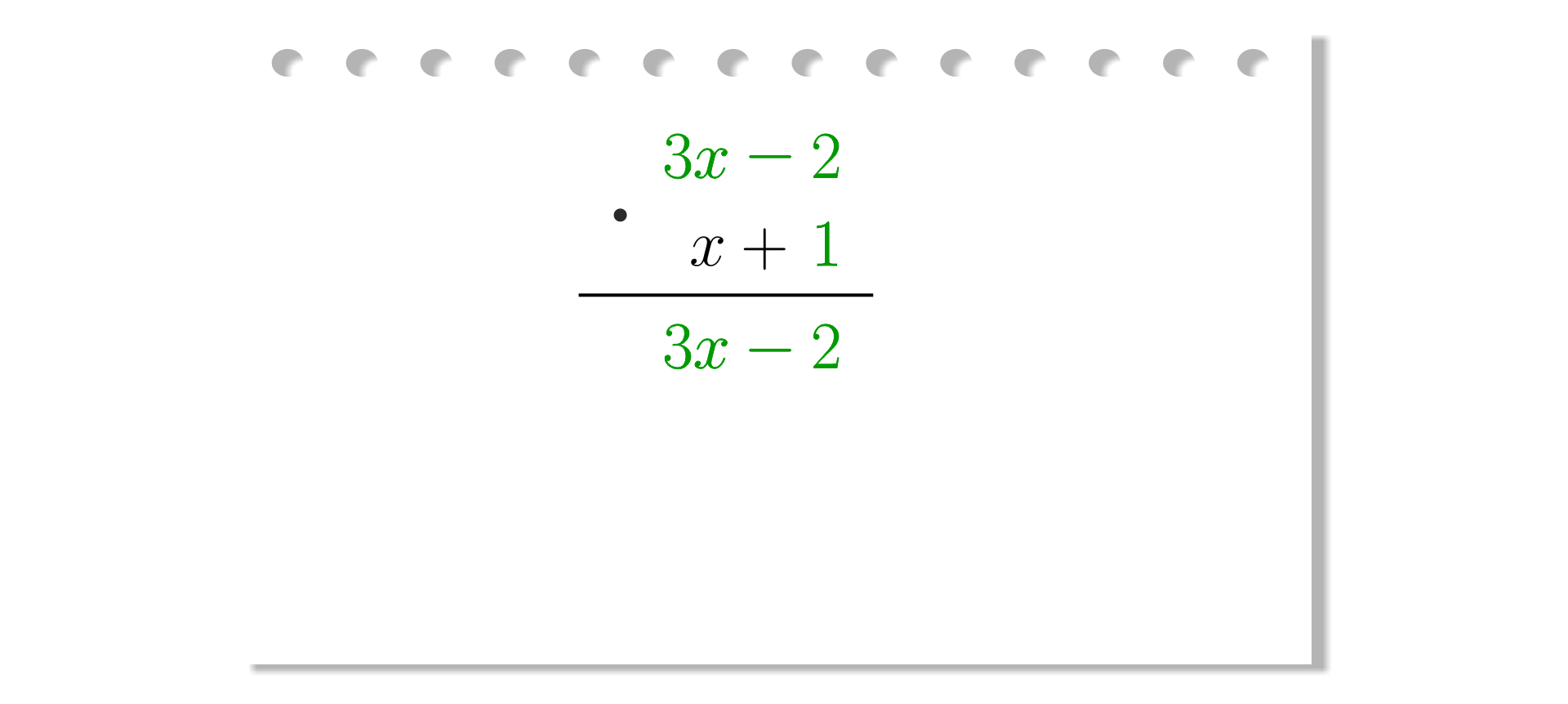
Krok
Mnożymy pierwszy dwumian przez .
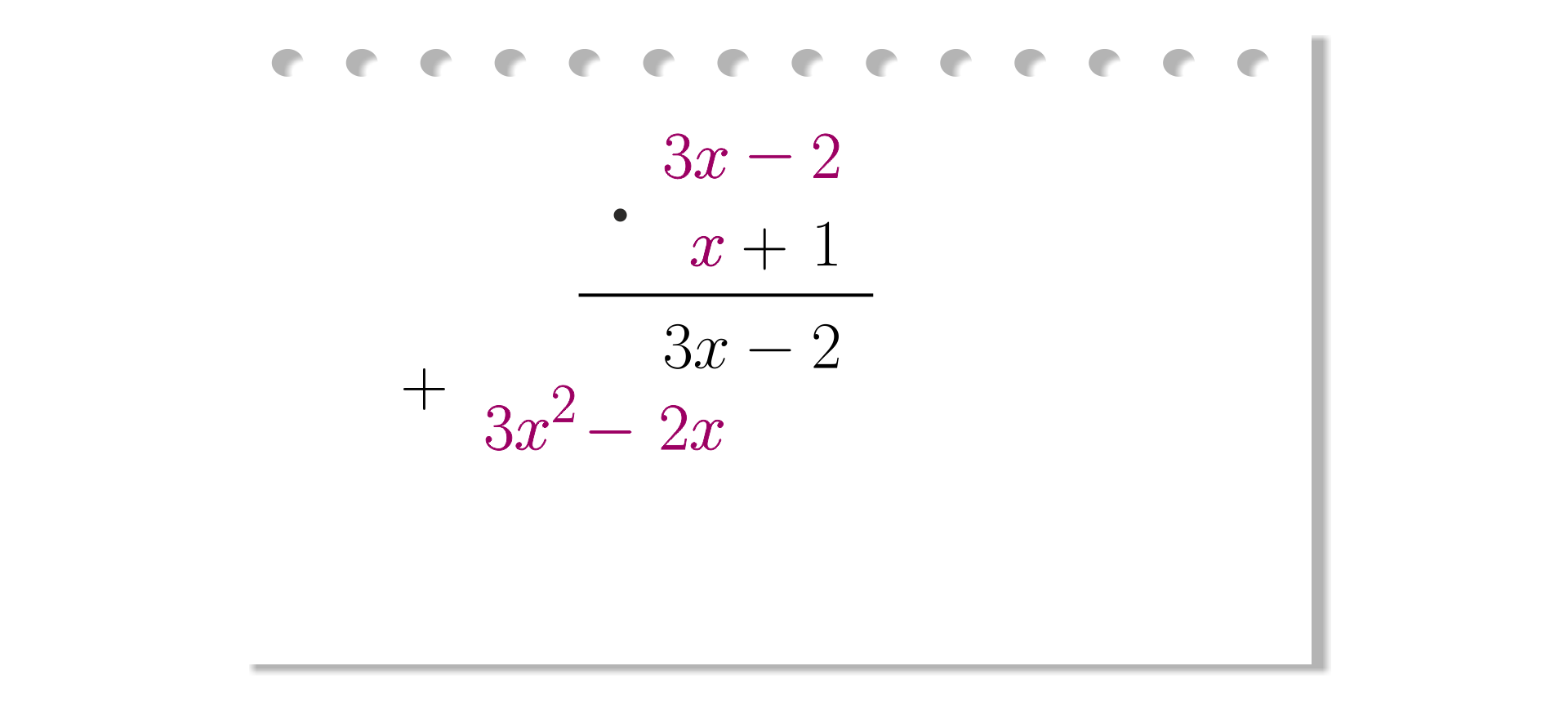
Krok
Dodajemy otrzymane wyrażenia i redukujemy wyrazy podobne.
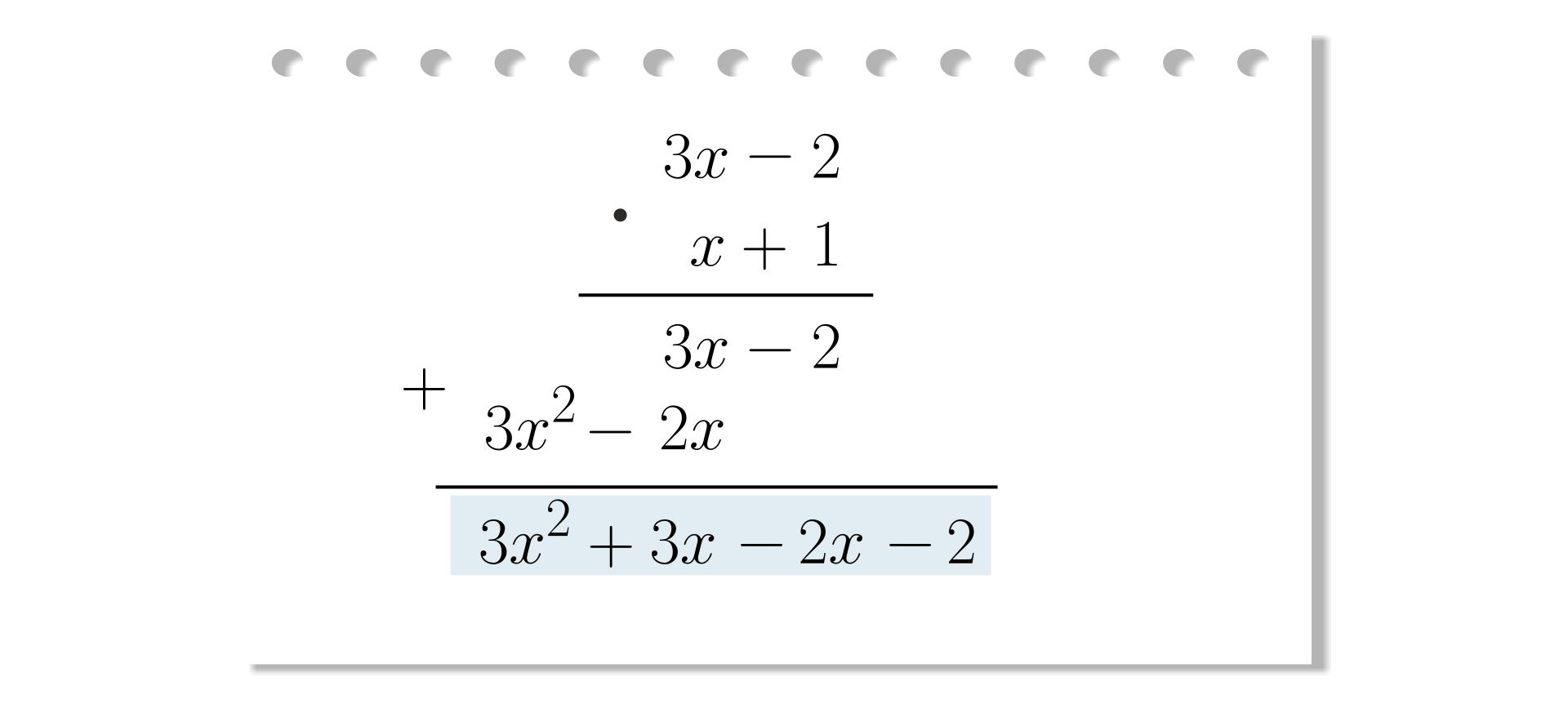
Poznane sposoby mnożenia można zastosować do mnożenia wyrażeń zawierających pierwiastki.
Zapiszemy w prostszej postaci wyrażenie .
Zauważmy, że: i .
Redukujemy wyrazy podobne.
Podstawą prostopadłościanu jest prostokąt o bokach długości i , gdzie . Wysokość tego prostopadłościanu jest równa . Zapiszemy wzór, który pozwoli na obliczenie objętości tego prostopadłościanu.
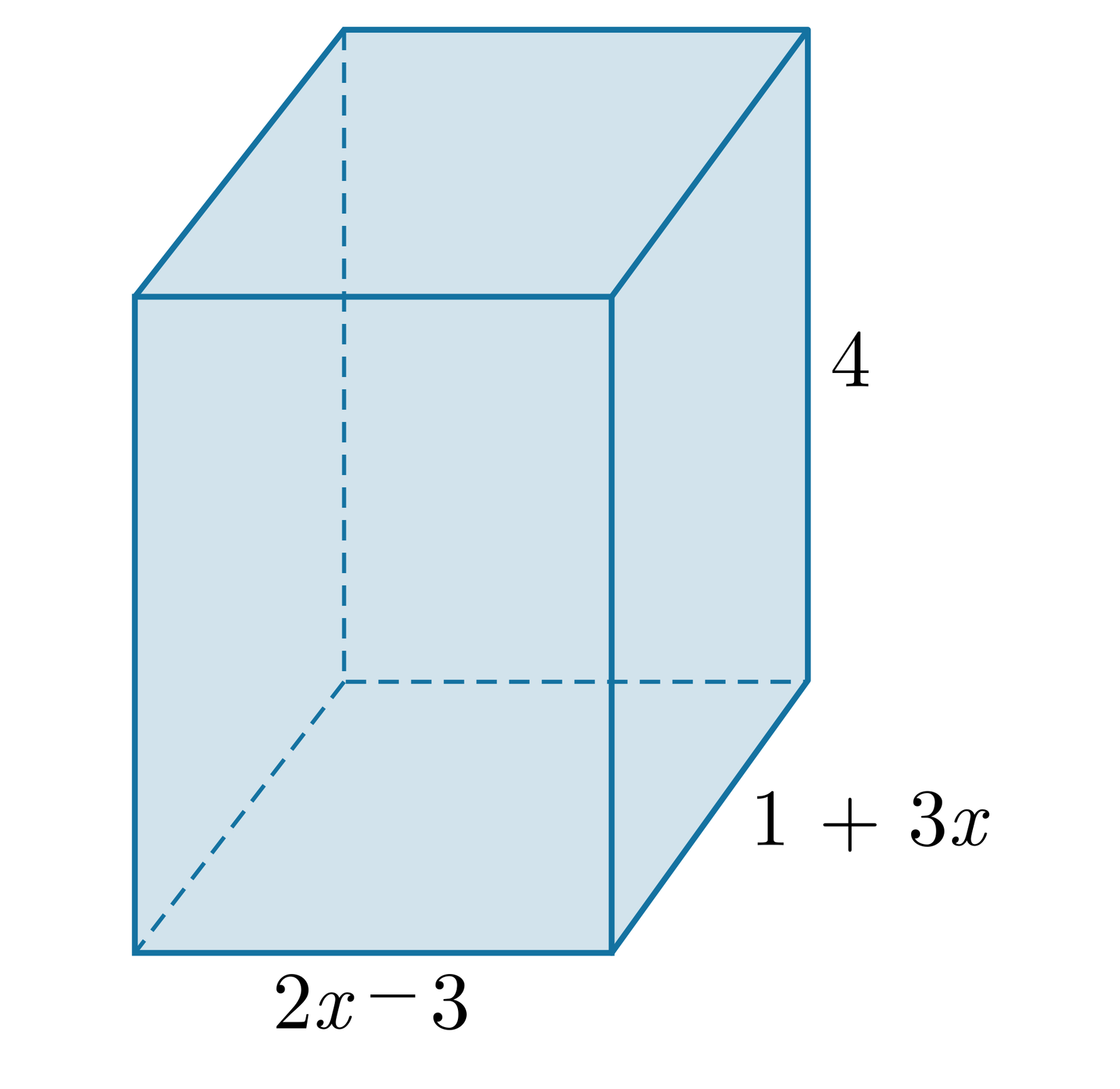
Aby obliczyć objętość prostopadłościanu, mnożymy wysokość prostopadłościanu przez pole podstawy tego prostopadłościanu.
W tym przypadku mnożymy najpierw pierwszą sumę przez , a następnie tak otrzymane wyrażenie mnożymy przez .
Notatki
Ilustracja interaktywna
Obejrzyj materiał ilustrujący różne sposoby zamiany iloczynu dwumianów na sumę.
Zapoznaj się z materiałem opisującym sposoby zamiany iloczynu dwumianów na sumę. Różne sposoby mnożenia dwumianów i .
Sposób pierwszy:
Korzystamy z rozdzielności mnożenia względem dodawania.
,
,
,
.
Drugi sposób:
Korzystamy z interpretacji graficznej.
Kolumna pierwsza | Kolumna druga | Kolumna trzecia |
|---|---|---|
Kolumna pierwsza | Kolumna druga | Kolumna trzecia |
|---|---|---|
,
.
Trzeci sposób:
Pomnożymy dwumiany pisemnie.
Mnożenie sposobem pisemnym: oraz .
Pod kreską zapisano:.
Pod spodem z jednym przesunięciem w lewą stronę zapisano:.
Pod kreską zapisano wynik:
,
.
Zapisz w najprostszej postaci wyrażenie , gdy i .
Skorzystaj z rozdzielności mnożenia względem dodawania.
Wykonaj mnożenie: .
Skorzystaj z interpretacji graficznej mnożenia.
Zapisz w najprostszej postaci wyrażenie
Zestaw ćwiczeń interaktywnych
Zaznacz prawidłowe dokończenie zdania. Wyrażenie algebraiczne opisujące pole prostokąta przedstawionego na rysunku to:
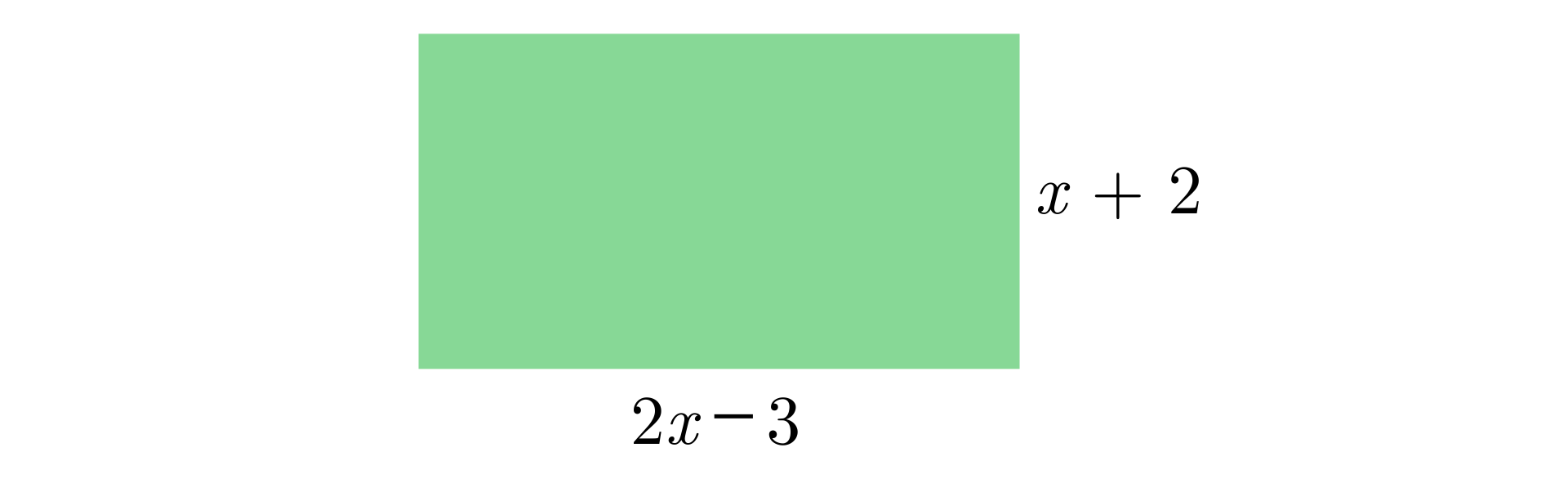
Tu uzupełnij
Tu uzupełnij
Tu uzupełnij
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
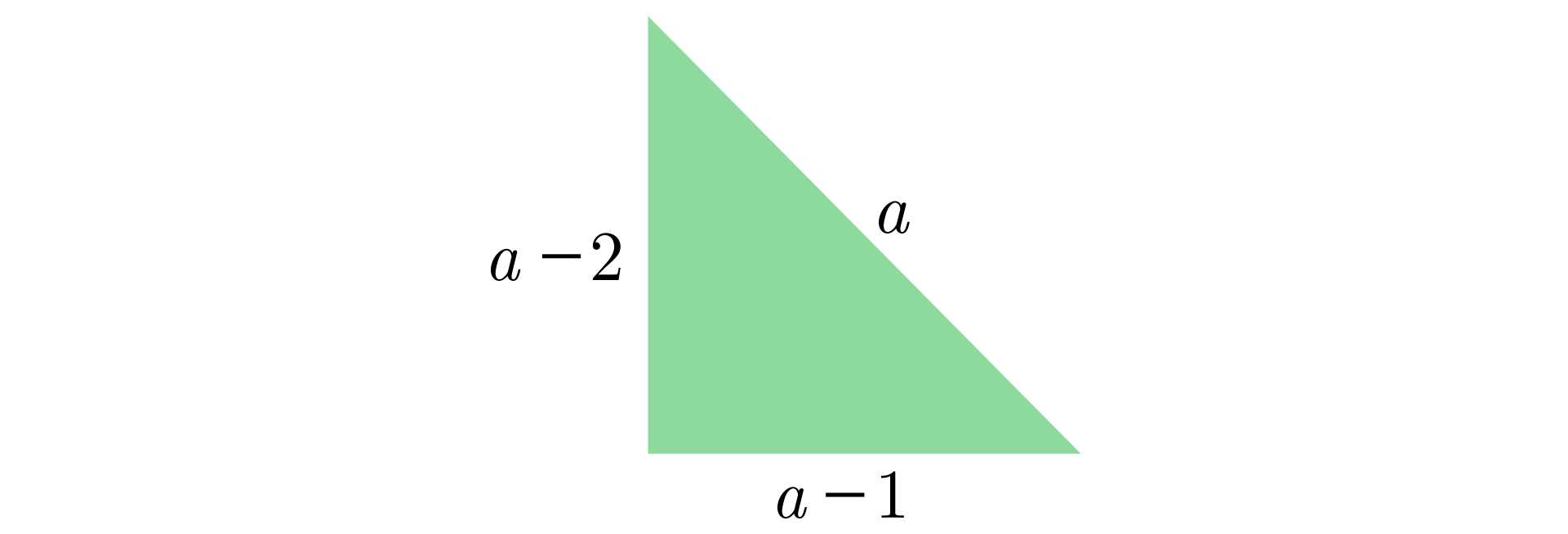
Uzasadnij, że liczba jest liczbą całkowitą.
Zapisz podane wyrażenie w postaci sumy i zredukuj wyrazy podobne.
Słownik
Aby pomnożyć dwie sumy algebraiczne, należy każdy wyraz pierwszej sumy pomnożyć przez każdy wyraz drugiej sumy i otrzymame jednomiany dodać.
Bibliografia
Darling D., Banerjee A., (2020), Jeszcze dziwniejsza matematyka. Na granicy poznania, Gliwice: Helion.