Niekonwencjonalne metody rozwiązywania zadań
W podręcznikach do nauczania matematyki z reguły zamieszczane są zadania tekstowe do samodzielnego rozwiązania przez uczniów. Podawane są też przykłady rozwiązania takich zadań. W klasach młodszych, proponuje się sposoby arytmetyczne, w klasach starszych – algebraiczne. Czasem warto zadanie rozwiązać graficznie lub po prostu zastosować logiczne rozumowanie.
Trudne zagadki matematyczne rozwiązywano już za czasów faraonów. Pasjonowano się nimi na dworach arystokratów w wieku, ogłaszano konkursy na odgadnięcie odpowiedzi. Obecnie większość z popularnych wtedy problemów, wydaje nam się dość proste. Bowiem współczesny aparat matematyczny pozwala na szybkie ustalenie odpowiedzi. Dlatego warto znać różne sposoby rozwiązywania zadań.
W tym materiale podamy różne sposoby rozwiązywania zadań tekstowych. Nie wyczerpiemy wszystkich możliwości, gdyż każdy może mieć własny pomysł na pokonanie problemu. Nie zawsze pewnie będzie to najkrótsza i najłatwiejsza droga, ale warto próbować. Gdyż nie w każdym przypadku można zastosować wyuczony algorytm.
Na początku proponujemy Ci rozwiązanie zadania zamieszczonego w książce Rozkosze łamania głowy autorstwa Lecha Pijanowskiego. Spróbuj rozwiązać je co najmniej trzema sposobami!

Rodzeństwo
Adam i Barbara są rodzeństwem.
Adam ma równie wielu braci, jak sióstr.
Barbara zaś ma dwa razy więcej braci niż sióstr.
Ile dzieci jest w tej rodzinie?
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
MultimediumMultimedium
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Przeanalizujesz zadanie tekstowe.
Wyodrębnisz w zadaniu dane i szukane.
Ustalisz strategię rozwiązania zadania tekstowego.
Rozwiążesz zadanie tekstowe dogodnym dla siebie sposobem.
Zadania tekstowe nie są lubiane przez uczniów, zwłaszcza, gdy tekst liczy więcej niż dwa wiersze. Zapis typu „rozwiąż równanie” jest zrozumiały, od razu wiadomo, do czego dążymy. Natomiast w zadaniu tekstowym to, czego szukamy, może być zawarte na początku, po środku lub na końcu tekstu. Co gorsza, może okazać się, że szukamy nie jednej, a kilku wielkości niewiadomych.
I czasem niezrozumienie treści zadania powoduje, że „stoimy w miejscu”.
Zatem naczelna zasada – dobre przeanalizowanie zadania i ustalenie niewiadomych. Dopiero wtedy możemy myśleć, jaki sposób rozwiązania wybrać.
Na początku zajmiemy się zadaniami prostymizadaniami prostymi, w których treść nie jest zbyt długa i które wymagają znalezienia tylko jednej wielkości lub dwóch wielkości tego samego rodzaju.
W sklepie było klientów. Gdy wyszło kilku klientów, w sklepie zostało jeszcze klientów. Ile klientów wyszło ze sklepu?
Szukana liczba klientów, którzy wyszli ze sklepu.
sposób
Sporządzamy odpowiedni rysunek – jedna kratka obrazuje jednego klienta.
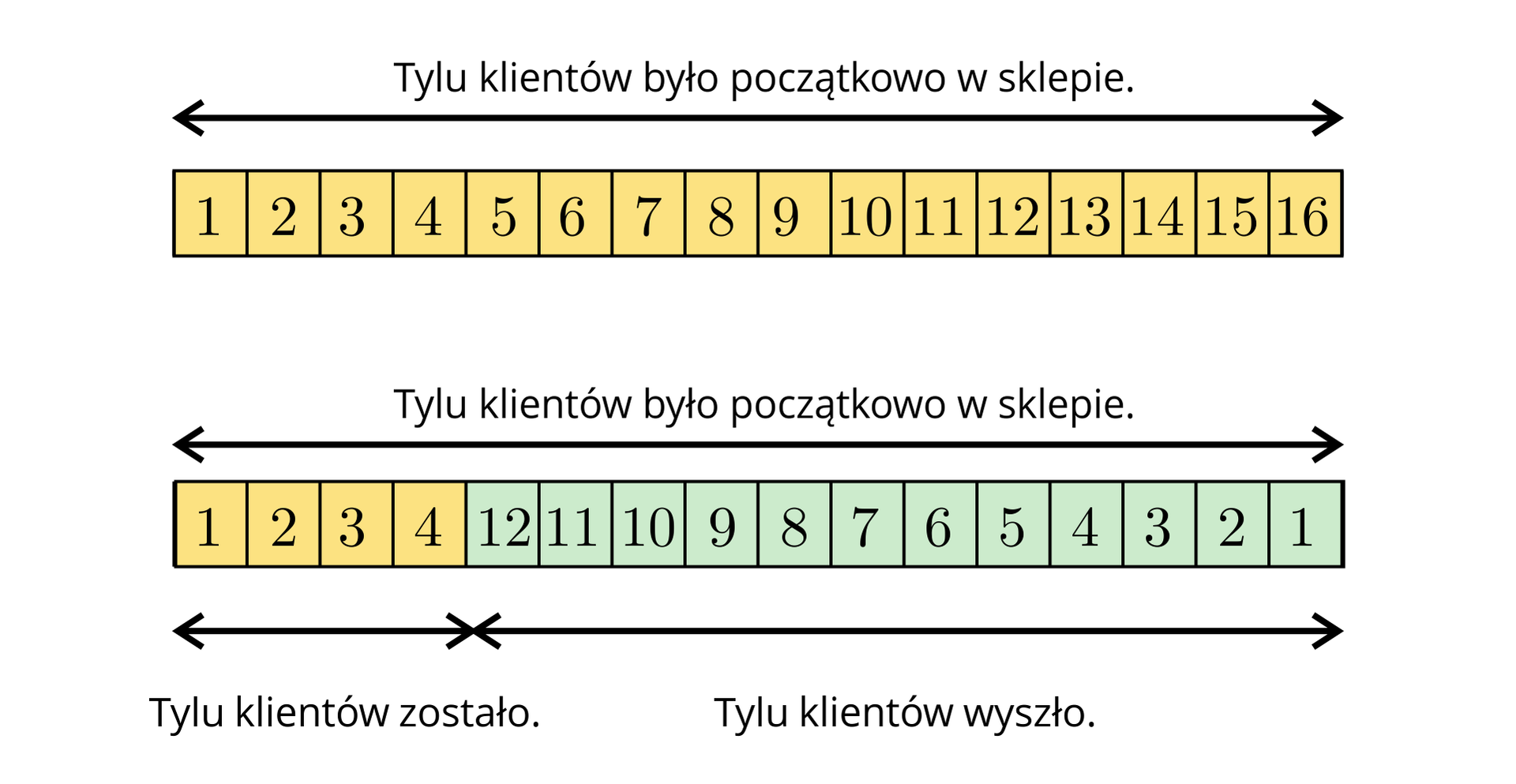
Z rysunku odczytujemy, że wyszło klientów.
sposób
Rysujemy graf i korzystamy z metody działań odwrotnych. Jednak, aby skorzystać z tej metody, musimy wiedzieć, że .
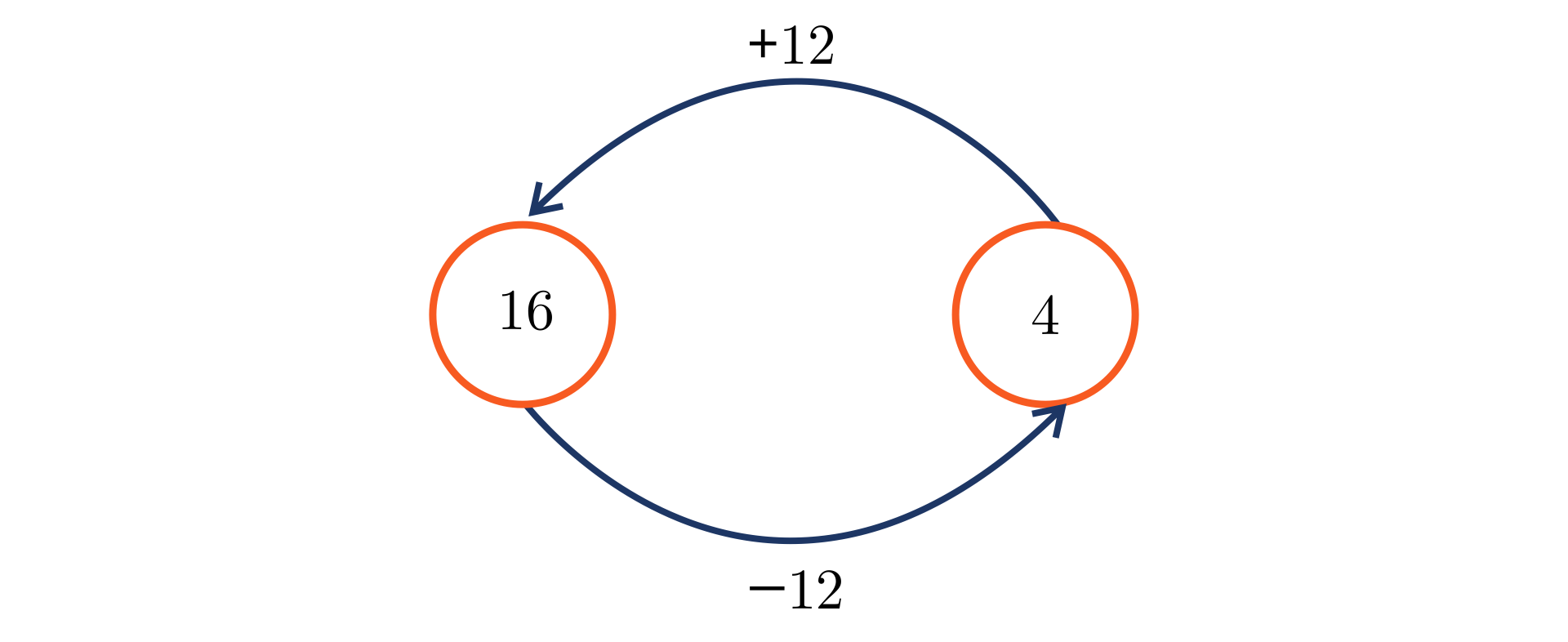
Z grafu odczytujemy, że wyszło klientów.
sposób
Układamy i rozwiązujemy odpowiednie równanie.
Oznaczamy przez liczbę klientów, którzy wyszli.
Wyszło klientów.
Tasiemkę długości przecięto na dwie części w stosunku . Jaką długość ma każda z tak otrzymanych części?
Szukane: długości części, na które podzielono tasiemkę.
sposób – metoda graficzna
Najpierw tasiemkę dzielimy na równych części – każda z tych części ma długości. To jest nasz rysunek pomocniczy.

Wiemy, że tasiemkę podzielono w stosunku .
Zatem na rysunku dokonujemy kolejnego podziału – tym razem na równych części.
Na rysunku widać, że każda z części będzie miała długości.

Teraz ustalamy długość dwóch i czterech z uzyskanych części.
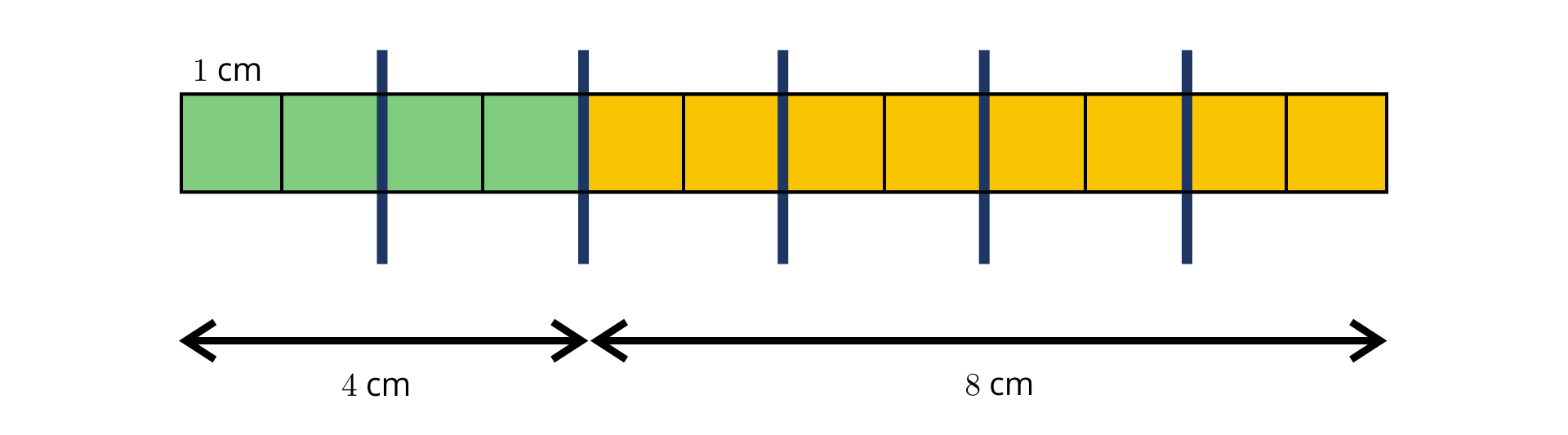
Z rysunku odczytujemy, że tasiemkę przecięto na części długości i .
sposób – metoda dedukcyjna
Zapisujemy stosunek określający podział tasiemki za pomocą ułamka zwykłego i skracamy.
Wnioskujemy, że jedna z części musi być dwa razy większa od drugiej, a . Zatem krótsza część ma długości, a dłuższa .
sposób – metoda prób i błędów
Sporządzamy odpowiednią tabelkę, którą wypełniamy tak długo, aż znajdziemy właściwy stosunek.
Ta metoda dobrze sprawdza się , gdy jest mało możliwości do rozpatrzenia, a wielkości szukane i dane wyrażają się liczbami całkowitymi. Nie gwarantuje jednak znalezienia wszystkich rozwiązań. Chyba, że rozpatrzymy wszystkie możliwości.
Długość krótszej części w | Długość dłuższej części w | Czy stosunek długości tych części jest równy ? |
|---|---|---|
Nie | ||
Nie | ||
Nie | ||
Tak | ||
Nie | ||
Nie |
Z tabelki odczytujemy odpowiedź – tasiemkę przecięto na części długości i .
Zauważmy, że w przykładzie , w sposobie i założyliśmy, że długości części, na jakie została podzielona tasiemka wyrażają się liczbami całkowitymi – a tego założenia nie było w treści zadania. Co prawda udało nam się znaleźć rozwiązanie, ale nie udowodniliśmy, że innego rozwiązania nie ma. Zatem możemy uznać, że takie sposoby postępowania są częściowo poprawne.
Przykład zadania prostegozadania prostego którego rozwiązanie znajdziemy, nie posługując się wzorami geometrycznymi.
Pani Ewa ma ogród w kształcie prostokąta o bokach długości i . Ile metrów bieżących siatki potrzebuje na ogrodzenie ogrodu, jeśli do ogrodu ma prowadzić brama wjazdowa o szerokości ?
Szukana: liczba metrów bieżących siatki.
Zadanie daje się łatwo rozwiązać, jeżeli znamy wzór na obwód prostokąta. A jeśli nie znamy takiego wzoru?
Możemy wtedy sporządzić odpowiedni rysunek „na kracie”. Zakładamy, że długość jednej kratki to .
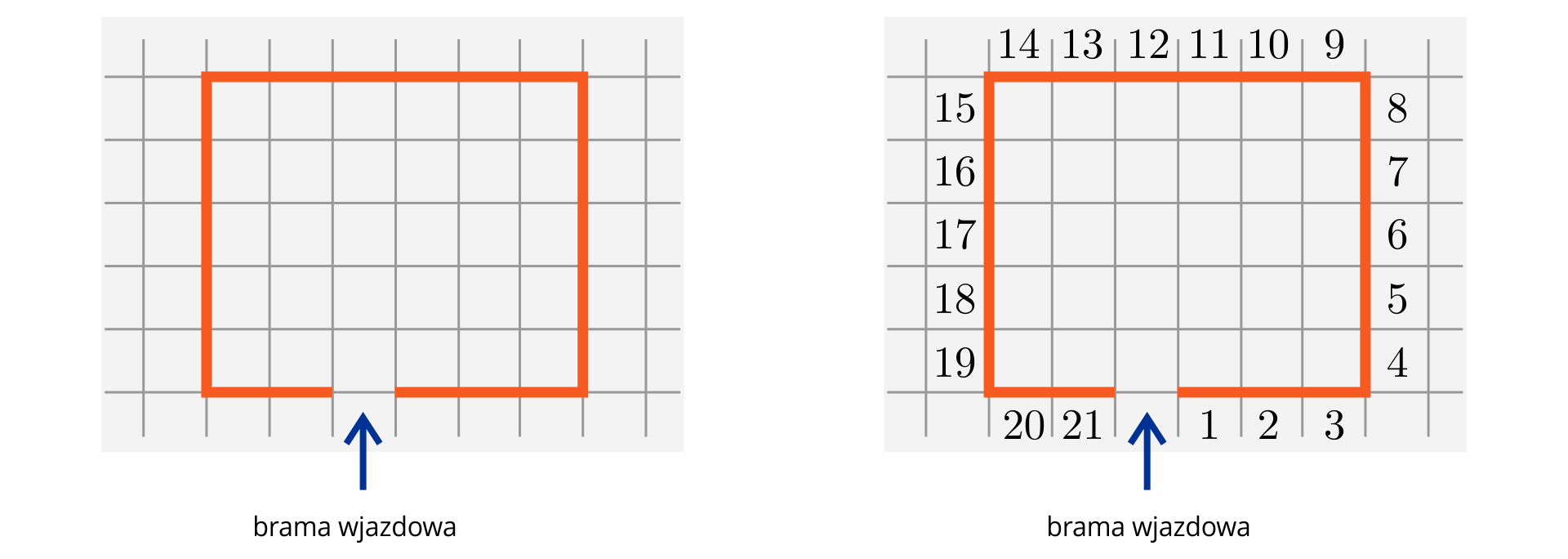
Na podstawie rysunku stwierdzamy, że długość narysowanej przez nas łamanej (obrazującej siatkę ogrodzeniową) jest równa .
Ale kratka ma długość , zatem na ogrodzenie pani Ewa potrzebuje
metrów siatki.
Nie zawsze z treści zadania można od razu wywnioskować, jakie wielkości należy „po drodze” znaleźć, aby uzyskać odpowiedź na postawione w zdaniu pytanie. Warto wtedy rozłożyć problem na kilka prostych tak, że liczba znaleziona jako wartość niewiadomej jednego zadania prostegozadania prostego jest zarazem daną następnego zadania prostego. Takie zadania tekstowe nazywamy czasem zadaniami łańcuchowymizadaniami łańcuchowymi.
Do składnicy opału przywieziono węgiel sześcioma ciężarówkami, każda o ładowności . Dostarczony węgiel popakowano do jednakowych worków, zawierających po węgla.
Pan Jakub kupił worków węgla, pani Krystyna . Ile worków węgla zostało jeszcze w składnicy?
Szukana: pozostała w składnicy liczba worków węgla.
– metoda łańcuchowa
Rozkładamy treść zadania na kawałki i wyznaczamy wartości liczbowe kolejnych wielkości.

Obliczamy, ile kilogramów węgla przywieziono.

Obliczamy, ile worków węgla otrzymano.

Obliczamy, ile zostało worków.
Odpowiedź: w składnicy zostało jeszcze worków węgla.
– metoda działań arytmetycznych
Układamy odpowiednie działanie arytmetyczne i wykonujemy obliczenia.
Odpowiedź: w składnicy zostało jeszcze worków węgla.
W bardziej skomplikowanych zadaniach tekstowych, określone są co najmniej dwa związki między niewiadomymi. Takie zadania można próbować rozwiązać za pomocą równania. Jednak przełożenie treści zadania na język matematyki, nie zawsze jest łatwe. W przypadku, gdy mamy dwie niewiadome, już sam wybór, którą zmienną uzależnimy od której, jest trudny. Może się bowiem okazać, że zły wybór skomplikuje równanie, które zapiszemy i które będzie trzeba rozwiązać.
Dlatego zawsze warto mieć plan awaryjny, zawierający inny sposób rozwiązania.
Na wycieczkę do Lublina wybrali się uczniowie z klasy A i z klasy B. Chłopców zakwaterowano w pokojach czteroosobowych, a dziewczęta w pokojach trzyosobowych. Przy czym pokoi trzyosobowych było dwa razy więcej niż czteroosobowych. Czy na tę wycieczkę mogło pojechać wszystkich uczniów?
sposób
Analiza zadania
– liczba pokoi czteroosobowych,
– liczba pokoi trzyosobowych,
– liczba chłopców, którzy pojechali na wycieczką,
– liczba dziewcząt, które pojechały na wycieczkę.
Układamy i rozwiązujemy odpowiednie równanie.
Liczba pokoi musi wyrażać się liczbą naturalną. Zatem na wycieczkę nie mogło pojechać uczniów.
sposób
Rozwiązanie zadania będzie przebiegało podobnie jak poprzednio, ale teraz za przyjmiemy inną wielkość.
Analiza zadania
– liczba pokoi trzyosobowych,
– liczba pokoi czteroosobowych,
– liczba dziewcząt, które pojechały na wycieczkę,
– liczba chłopców, którzy pojechali na wycieczkę.
Układamy i rozwiązujemy odpowiednie równanie.
Liczba pokoi musi wyrażać się liczbą naturalną. Zatem na wycieczkę nie mogło pojechać uczniów.
sposób
Ponieważ zarówno ilość osób, jak i ilość pokoi muszą wyrażać się liczbami naturalnymi, zatem możemy sporządzić pomocniczą tabelkę i poszukać możliwego rozwiązania.
Liczba pokoi czteroosobowych | Liczba pokoi trzyosobowych | Liczba wszystkich uczniów zakwaterowanych w pokojach | Czy liczba ta jest równa ? |
|---|---|---|---|
Za mało | |||
Za mało | |||
Za mało | |||
Za mało | |||
Za dużo |
Wyciągamy wniosek taki, jak poprzednio: na wycieczkę nie mogło pojechać uczniów.
sposób
Zauważmy, że z treści zadania wynika, że był zajęty co najmniej jeden pokój czteroosobowy i co najmniej dwa pokoje trzyosobowe. Zatem wszystkich uczniów było najmniej . Otrzymujemy, że liczba uczniów musi być wielokrotnością liczby , czyli na wycieczką nie mogło pojechać uczniów.
Notatki
Animacja
Zapoznaj się z animacją. Spróbuj rozwiązać każde z podanych tam zadań swoim sposobem, a dopiero następnie porównaj z podanym rozwiązaniem.

Film dostępny pod adresem /preview/resource/Rf6dlKlaO8bxW
Animacja nawiązująca do treści materiału.
Rozwiąż za pomocą równania zadanie zaprezentowane w animacji. Oznacz przez liczbę jabłek leżących na stole.
Wzorując się na rozwiązaniu zadania z animacji, znajdź odpowiedź na pytanie postawione w poniższym zadaniu.
Przekupka miała w koszyku jajka. Pani Ania kupiła od niej połowę jajek i jeszcze jedno jajko. Pani Basia kupiła połowę pozostałych jajek i jeszcze dwa jajka. Pani Czesia kupiła połowę pozostałych jajek i jeszcze jedno jajko. Pani Danka kupiła pozostałe cztery jajka. Ile jajek miała przekupka początkowo w koszyku?
Zeszyt w kratkę jest o droższy od zeszytu w linie. Za zeszyty w kratkę i zeszyty w linie zapłacono łącznie . Oblicz cenę jednego zeszytu w kratkę. Rozwiąż zadanie w sposób arytmetyczny.
Zestaw ćwiczeń interaktywnych
O ilu więcej uczniów lubi lody malinowe niż czekoladowe?
Pan B stoi przed panem D.
Pan A nie stoi obok pana C.
Pan C nie stoi obok pana D.
Pan A ma tylko jednego sąsiada.
Które ustawienie poprawnie opisuje ustawienie panów A, B, C, D?
Pięć lat temu pani Zielińska miała tyle lat, ile pan Zieliński miał dziesięć lat temu. Za pięć lat Zbyszek będzie trzy razy młodszy od taty.
Zaznacz, które zdanie jest prawdziwe, a które fałszywe.. Zula jest obecnie siedem razy młodsza od mamy.. Możliwe odpowiedzi: Prawda, Fałsz. Pani Zielińska jest o lat starsza od syna.. Możliwe odpowiedzi: Prawda, Fałsz. Zbyszek jest razy starszy od Zuli.. Możliwe odpowiedzi: Prawda, Fałsz. Ojciec jest razy starszy od syna.. Możliwe odpowiedzi: Prawda, Fałsz. Za lat pani Zielińska będzie trzy razy starsza od córki.. Możliwe odpowiedzi: Prawda, Fałsz. Za lat Zula będzie miała tyle lat, ile Zbyszek ma teraz.. Możliwe odpowiedzi: Prawda, Fałsz
Poniżej wykonano ilustrację graficzną treści zadania. Zaznacz, na którym rysunku przedstawiona jest tasiemka, na którym sznurek, a na którym drut - przeciągnij odpowiednie nazwy.
W kawiarni stolików mających trzy nogi jest o więcej niż stolików mających cztery nogi. Razem stoliki mają nóg. Ile jest w tej kawiarni stolików mających trzy nogi?
Rozwiąż zadanie, nie korzystając z równania.
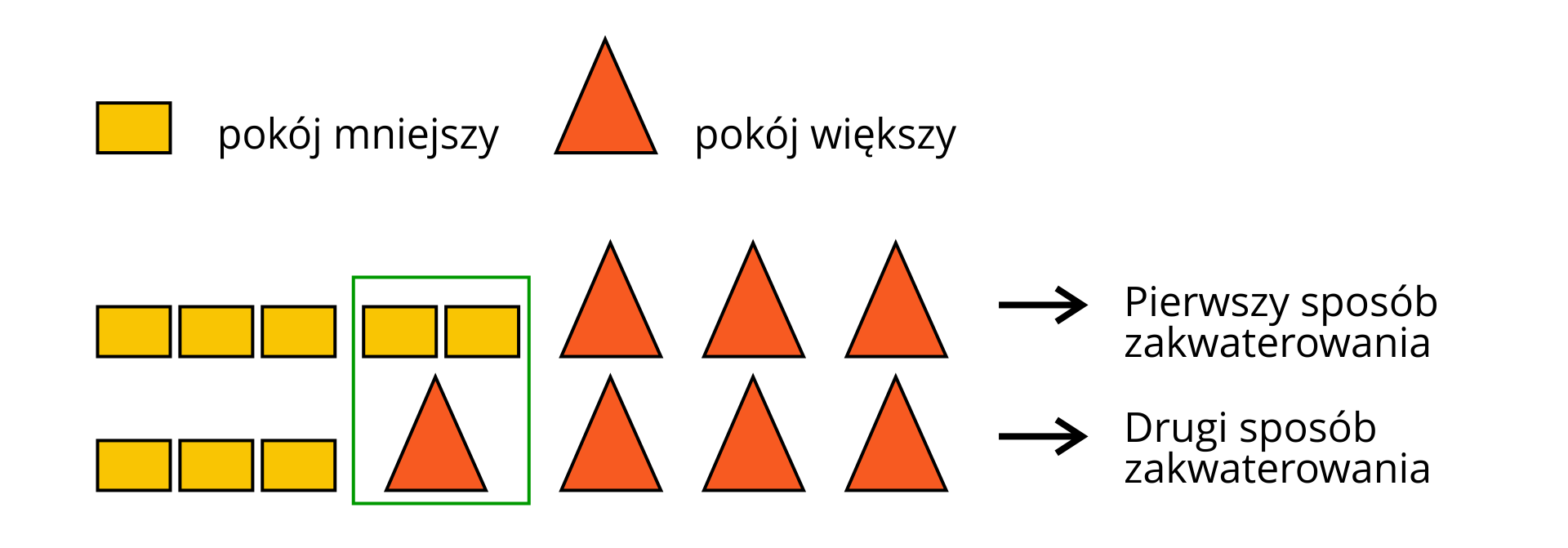
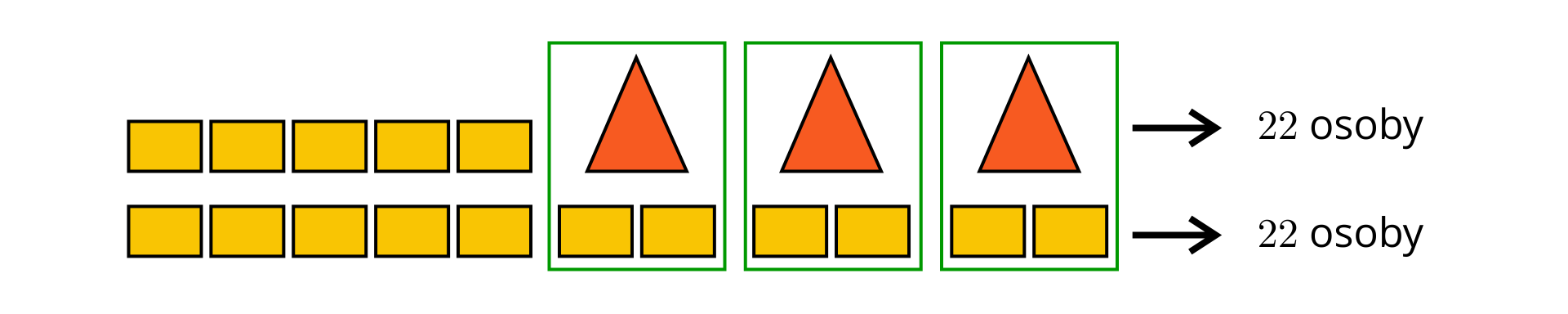
Na górską wycieczkę wybrało się uczniów. Mogą zostać zakwaterowani w schronisku w pięciu mniejszych pokojach i trzech większych pokojach lub czterech pokojach większych i trzech mniejszych.
Oblicz, w ilu mniejszych pokojach mogliby zostać zakwaterowani uczestnicy wycieczki.
Aby rozwiązać zadanie, sporządź odpowiedni rysunek.
Autobus pokonuje pewną trasę w ciągu pół godziny, a samochód tę trasę pokonuje w ciągu dwudziestu minut.
Po ilu minutach samochód dogoni autobus, jeżeli wyruszył z tego samego miejsca minut po autobusie? Rozwiąż zadanie, nie korzystając z równania.
Słownik
zadanie którego rozwiązanie wymaga znalezienia jednej wielkości lub dwóch wielkości tego samego rodzaju.
zadanie, które można rozłożyć na ciąg zadań prostych tak, że liczba znaleziona jako wartość niewiadomej jednego zadania prostego wchodzi jako dana do następnego zadania w łańcuchu.
Bibliografia
Steinhaus H., (1993), 100 zadań, Warszawa: PHU DIP.