Nierówność kwadratowa

W tym materiale zawarte są przykłady rozwiązywania nierówności kwadratowych. Po przeanalizowaniu zadań, możesz sprawdzić swoje umiejętności, samodzielnie znajdując zbiory rozwiązań nierówności zapisanych w ćwiczeniach.

Przykład 1

Na podstawie wykresu funkcji kwadratowej $f$ określonej wzorem $f (x) = (x - 1) (x + 3)$ ustalimy zbiór rozwiązań nierówności $(x - 1) (x + 3) > 0$ oraz nierówności $(x - 1) (x + 3) < 0$ .

RQFLa68Y2kN0U1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

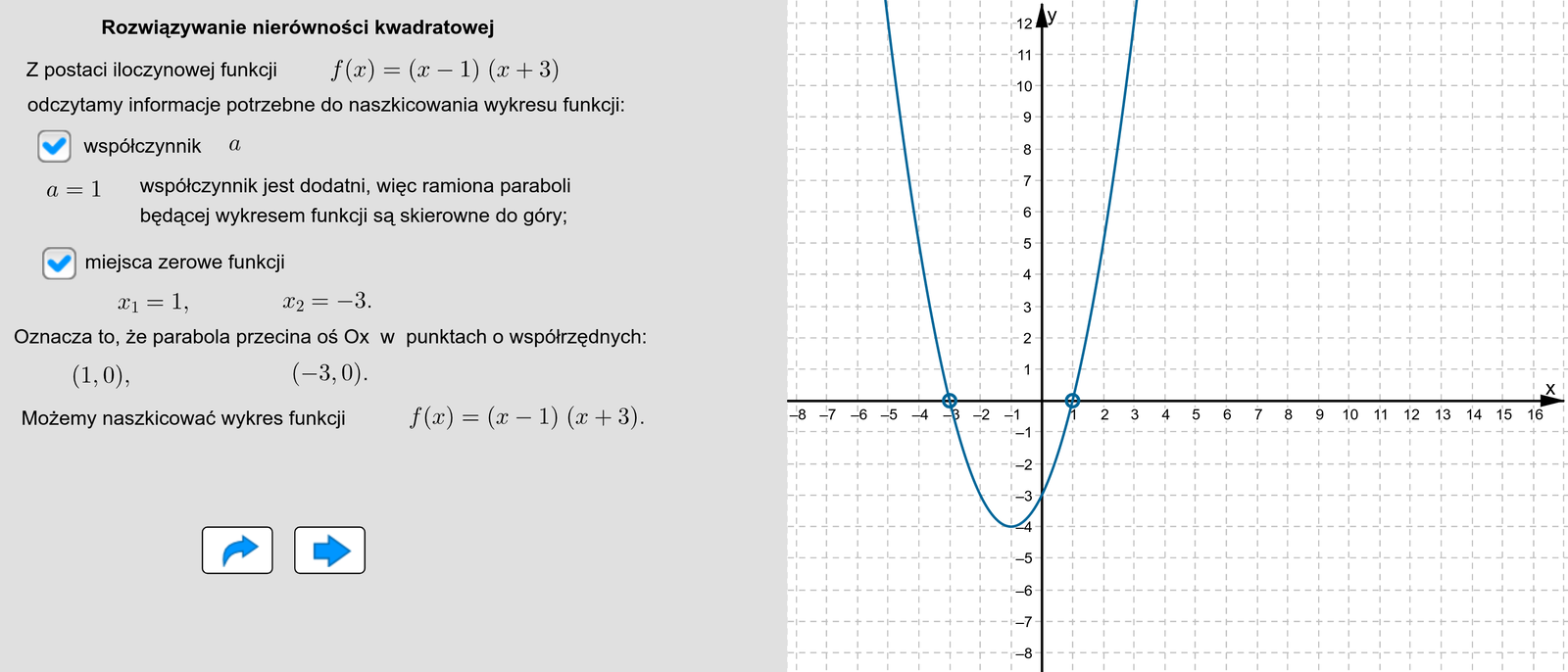
Z postaci iloczynowej wzoru funkcji $f$

f (x) = 1 \cdot (x - 1) (x + 3)

bezpośrednio odczytujemy:

współczynnik $a$ : $a = 1$ . Jest on dodatni, więc parabola będąca wykresem funkcji $f$ ma ramiona skierowane do góry,
miejsca zerowe funkcji $f : 1$ oraz $(- 3)$ . Oznacza to, że wykres funkcji $f$ przecina oś $X$ w dwóch punktach o współrzędnych $(1, 0)$ oraz $(- 3, 0)$ .

Korzystając z powyższych spostrzeżeń, szkicujemy wykres funkcji $f$ .

RdL3H0HePbsoc1

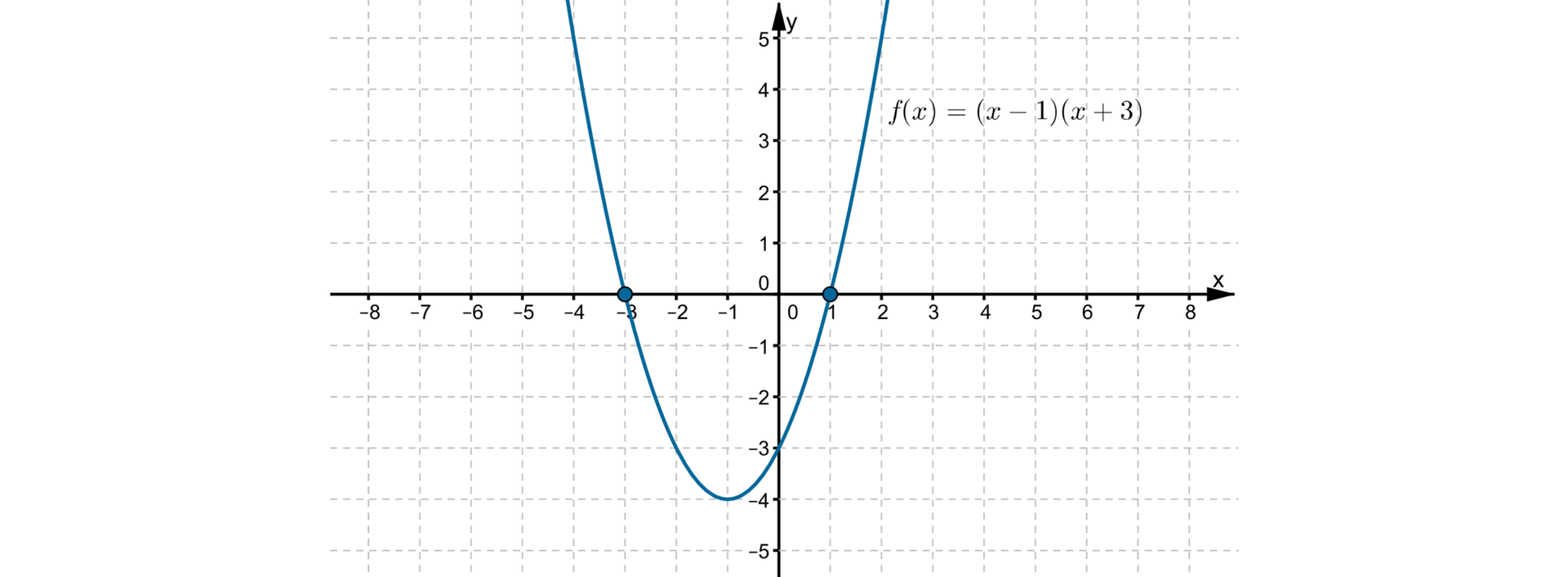
Wykres funkcji f(x) =(x -1) razy (x +3). Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus ośmiu do ośmiu oraz pionową osią Y od minus pięciu do pięciu. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi ku górze. Parabola przecina poziomą oś w punktach o współrzędnych:-3,0, 1,0. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ustalimy zbiór rozwiązań nierówności $(x - 1) (x + 3) > 0$ .

Z otrzymanego wykresu odczytujemy, dla jakich argumentów funkcja $f$ przyjmuje wartości dodatnie.

RYfs5HUicalEx1

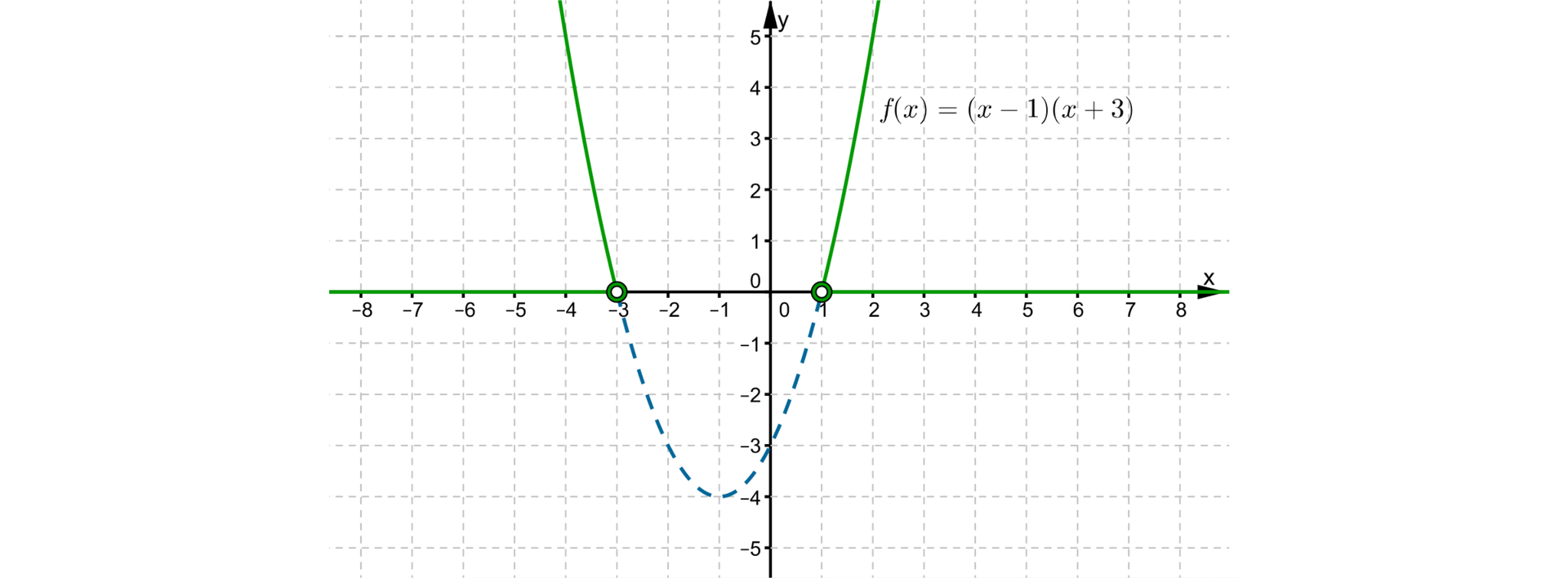
Wykres funkcji f(x) =(x -1) razy (x +3), na którym zaznaczono rozwiązanie nierówności (x -1) razy (x +3) >0, czyli przedział -∞,-3∪1,+∞. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zatem $(x - 1) (x + 3) > 0$ wtedy i tylko wtedy, gdy $x \in (- \infty, - 3) \cup (1, + \infty)$ .

Ustalimy zbiór rozwiązań nierówności $(x - 1) (x + 3) < 0$ .

Z wykresu funkcji $f$ odczytujemy, dla jakich argumentów ta funkcja przyjmuje wartości ujemne.

RjT7PuXPuKIqu1

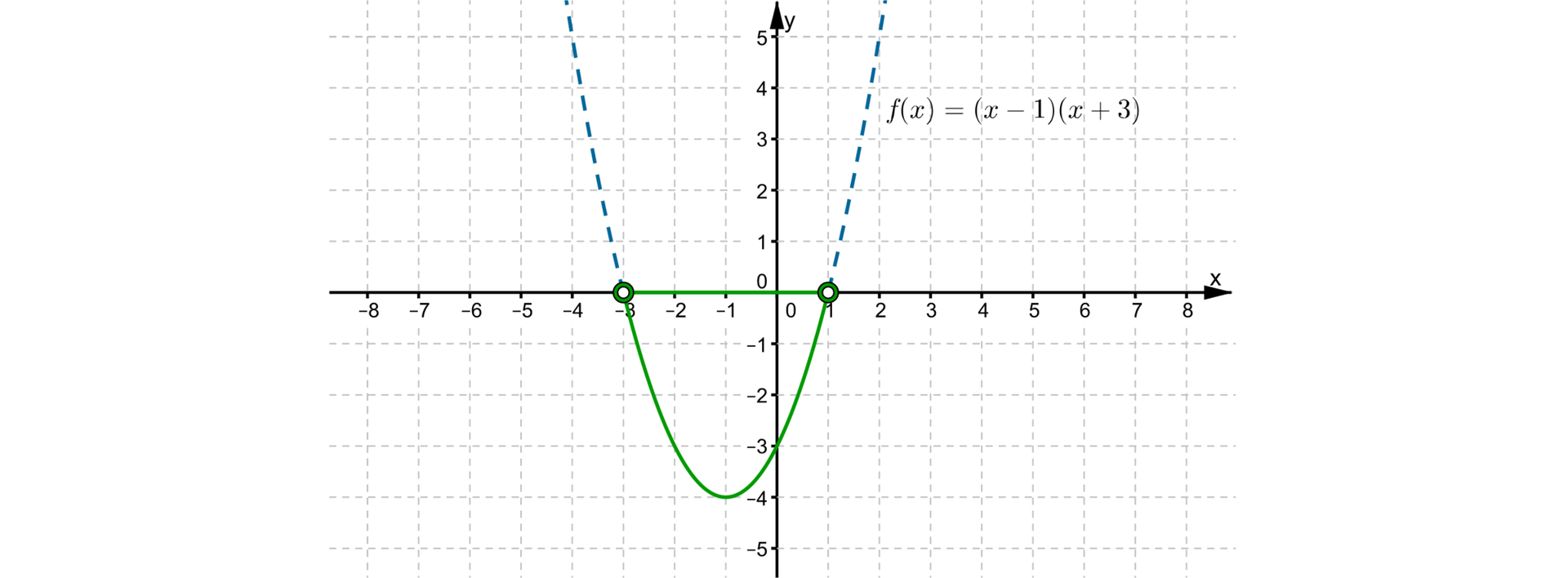
Wobec tego $(x - 1) (x + 3) < 0$ wtedy i tylko wtedy, gdy $x \in (- 3, 1)$ .

Przykład 2

Wypiszemy wszystkie liczby całkowite, które spełniają nierówność $(2 x + 5) (4 - x) > 0$ .

Rozpatrzmy w tym celu funkcję kwadratową określoną wzorem $f (x) = (2 x + 5) (4 - x)$ .

Po zapisaniu wzoru tej funkcji w postaci iloczynowej $f (x) = - 2 (x + \frac{5}{2}) (x - 4)$ stwierdzamy, że

funkcja ta ma dwa miejsca zerowe $(- \frac{5}{2})$ oraz $4$ ,

$a = - 2 < 0$ , zatem wykresem tej funkcji jest parabola skierowana ramionami do dołu.

Szkicujemy wykres funkcji $f (x) = (2 x + 5) (4 - x)$ i zaznaczamy na nim argumenty, dla których $(2 x + 5) (4 - x) > 0$ .

R1FuEz9cwtIxQ1

Wykres funkcji f(x) =(2x +5) razy (4 –x) z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 20 do 20 oraz pionową osią Y od minus 2 do 20. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi do dołu. Parabola przecina poziomą oś w punktach o współrzędnych:-2,0, 4,0. Na wykresie zaznaczono przedział -2,4. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zbiorem rozwiązań nierówności $(2 x + 5) (4 - x) > 0$ jest więc przedział $(- 2 \frac{1}{2}, 4)$ .

Zaznaczamy wszystkie liczby całkowite, które znajdują się w tym przedziale.

R14CpJtOcgOem1

Rysunek przedziału liczbowego obustronnie otwartego od -2,5 do czterech. Wewnątrz przedziału zaznaczone liczby całkowite -2, -1, 0, 1, 2, 3 będące rozwiązaniem przykładu. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ostatecznie stwierdzamy, że liczbami całkowitymi, które spełniają nierówność $(2 x + 5) (4 - x) > 0$ , są: $(- 2)$ , $(- 1)$ , $0$ , $1$ , $2$ , $3$ .

Przykład 3

Rozwiążemy nierówność

$x^{2} - 9 > 0$
Wykresem funkcji kwadratowej określonej wzorem $f (x) = x^{2} - 9$ jest parabola skierowana ramionami do góry, co stwierdzamy, odczytując ze wzoru tej funkcji wartość współczynnika $a$ : $a = 1 > 0$ .
Wzór tej funkcji przekształcamy do postaci $f (x) = (x - 3) (x + 3)$ . Funkcja ma zatem dwa miejsca zerowe $(- 3)$ oraz $3$ .
Szkicujemy wykres tej funkcji i odczytujemy wszystkie argumenty, dla których przyjmuje ona wartości dodatnie.
R44KLXDqLJ1WF1
Wykres funkcji f(x) = x kwadrat –9 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus 10 do 10 oraz pionową osią $Y$ od minus 10 do 10. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola przecina poziomą oś w punktach o współrzędnych: $(- 3, 0)$ , $(3, 0)$ . Na wykresie zaznaczono przedział $(- \infty, - 3) \cup (3, + \infty)$ .
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Odpowiedź: $x \in (- \infty, - 3) \cup (3, + \infty)$ .
$- x^{2} + 4 x < 0$

sposób $I$
Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = - x^{2} + 4 x$ . Odczytujemy wartość współczynnika $a : a = - 1 < 0$ . Wykresem tej funkcji jest parabola, której ramiona skierowane są w dół.
Wzór tej funkcji sprowadzamy do postaci iloczynowej $f (x) = - x (x - 4)$ i stwierdzamy, że funkcja ta ma dwa miejsca zerowe $0$ oraz $4$ .
Sporządzamy szkic wykresu funkcji $f (x) = - x^{2} + 4 x$ i na jego podstawie wyznaczamy zbiór rozwiązań nierówności $- x^{2} + 4 x < 0$ .
R1VxpQoQQQAOL1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Odpowiedź: $x \in (- \infty, 0) \cup (4, \infty)$ .
sposób $II$
Przekształcamy daną nierówność. Po pomnożeniu obustronnie przez $(- 1)$ otrzymujemy równoważnie
$x^{2} - 4 x > 0$ . Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = x^{2} - 4 x$ . Odczytujemy: $a = 1 > 0$ , zatem wykresem tej funkcji jest parabola, której ramiona skierowane są do góry.
Po zapisaniu wzoru tej funkcji w postaci iloczynowej $f (x) = x (x - 4)$ stwierdzamy, że funkcja ta ma dwa miejsca zerowe: $0$ oraz $4$ .
Sporządzamy szkic wykresu funkcji $f (x) = x^{2} - 4 x$ i na jego podstawie wyznaczamy zbiór tych liczb rzeczywistych $x$ , dla których $x^{2} - 4 x > 0$ .
RJ6ltn0CVxHd61
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Odpowiedź: $x \in (- \infty, 0) \cup (4, \infty)$ .

Przykład 4

Rozwiążemy nierówność $x^{2} + 2 x + 1 > 0$ .

Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = x^{2} + 2 x + 1$ . Przekształcamy ten wzór do postaci $f (x) = {(x + 1)}^{2}$ . Ponieważ: $a = 1 > 0$ oraz funkcja ma jedno miejsce zerowe: $(- 1)$ , więc wykresem tej funkcji jest parabola skierowana ramionami w górę.

Szkicujemy wykres funkcji $f (x) = x^{2} + 2 x + 1$ i zaznaczamy argumenty, dla których $x^{2} + 2 x + 1 > 0$ .

R1COsIpSCeNlA1

Wykres funkcji f(x) =x kwadrat +2x +1 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 7 do 7 oraz pionową osią Y od minus 3 do 5. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola ma wierzchołek w punkcie o współrzędnych: -1,0. Na wykresie zaznaczono przedział -∞,-1∪-1,+∞. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź: $x \in (- \infty, - 1) \cup (- 1, + \infty)$ .

$x^{2} + 3 < 0$
Ponieważ $x^{2} ⩾ 0$ dla każdej liczby rzeczywistej $x$ , więc $x^{2} + 3 > 0$ dla każdego rzeczywistego $x$ . Zatem żadna liczba rzeczywista nie spełnia nierówności $x^{2} + 3 < 0$ .
Odpowiedź: Nierówność $x^{2} + 3 < 0$ jest sprzeczna.
$- x^{2} - 1 < 0$
Przekształcamy daną nierówność. Po pomnożeniu obustronnie przez $(- 1)$ otrzymujemy równoważnie $x^{2} + 1 > 0$ . Ponieważ suma liczby nieujemnej $x^{2}$ oraz liczby dodatniej $1$ jest liczbą dodatnią, więc każda liczba rzeczywista $x$ spełnia nierówność $x^{2} + 1 > 0$ .
Odpowiedź: Nierówność $- x^{2} - 1 < 0$ jest spełniona przez każdą liczbę rzeczywistą.

Przykład 5

Rozwiążemy nierówność $x^{2} - 12 x + 11 ⩽ 0$ .

Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = x^{2} - 12 x + 11$ . Odczytujemy: $a = 1 > 0$ , zatem wykresem tej funkcji jest parabola, której ramiona skierowane są do góry.

Obliczamy wyróżnik funkcji $f (x) = x^{2} - 12 x + 11$ :

$Δ = {(- 12)}^{2} - 4 \cdot 1 \cdot 11 = 100 > 0$ . Wobec tego funkcja $f (x) = x^{2} - 12 x + 11$ ma dwa miejsca zerowe

$x_{1} = \frac{12 - \sqrt{100}}{2} = 1$ oraz $x_{2} = \frac{12 + \sqrt{100}}{2} = 11$ .

Sporządzamy szkic wykresu tej funkcji i na jego podstawie ustalamy zbiór rozwiązań nierówności $x^{2} - 12 + 11 ⩽ 0$ .

RhjRI2Y5TPKLX1

Wykres funkcji f(x) = x kwadrat -12x +11 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 32 do 32 oraz pionową osią Y od minus 24 do 8. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola przecina poziomą oś w punkcie o współrzędnych 1,0 , 11,0. Na wykresie zaznaczono przedział 1,11. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź: $x \in ⟨1, 11⟩$ .

Przykład 6

Rozwiążemy nierówność $2 x^{2} + 7 x - 4 > 0$ .

Ze wzoru funkcji $f (x) = 2 x^{2} + 7 x - 4$ odczytujemy wartość współczynnika $a$ : $a = 2 > 0$ . Wobec tego wykresem tej funkcji jest parabola, której ramiona skierowane są do góry.

Obliczamy wyróżnik: $Δ = 7^{2} - 4 \cdot 2 \cdot (- 4) = 81 > 0$ , zatem funkcja $f (x) = 2 x^{2} + 7 x - 4$ ma dwa miejsca zerowe

$x_{1} = \frac{- 7 - \sqrt{81}}{2 \cdot 2} = - 4$ oraz $x_{2} = \frac{- 7 + \sqrt{81}}{2 \cdot 2} = \frac{1}{2}$ .

Sporządzamy szkic wykresu tej funkcji i na jego podstawie ustalamy zbiór rozwiązań nierówności $2 x^{2} + 7 x - 4 > 0$ .

RackiWttBbky51

Wykres funkcji f(x) =2x kwadrat +7x -4 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 16 do 16 oraz pionową osią Y od minus 10 do 6. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola przecina poziomą oś w punktach o współrzędnych:-4,0, 12,0. Na wykresie zaznaczono przedział -∞,-4∪12,+∞. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź: $x \in (- \infty, - 4) \cup (\frac{1}{2}, + \infty)$ .

Przykład 7

Rozwiążemy nierówność $- x^{2} + 3 x + 10 ⩾ 0$ .

Przekształcamy daną nierówność. Po pomnożeniu obustronnie przez $(- 1)$ otrzymujemy równoważnie

x^{2} - 3 x - 10 ⩽ 0

Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = x^{2} - 3 x - 10$ . Ponieważ $a = 1 > 0$ , więc wykresem tej funkcji jest parabola, której ramiona skierowane są do góry.

Obliczamy wyróżnik: $Δ = {(- 3)}^{2} - 4 \cdot 1 \cdot (- 10) = 49 > 0$ . Zatem funkcja $f (x) = x^{2} - 3 x - 10$ ma dwa miejsca zerowe $x_{1} = \frac{3 - \sqrt{49}}{2} = - 2$ oraz $x_{2} = \frac{3 + \sqrt{49}}{2} = 5$ .

Sporządzamy szkic wykresu tej funkcji i na jego podstawie wyznaczamy argumenty, dla których $x^{2} - 3 x - 10 ⩽ 0$ .

RaxHA7qLjddHz1

Wykres funkcji f(x) =x kwadrat -3x -10 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 18 do 18 oraz pionową osią Y od minus 12 do 6. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola przecina poziomą oś w punktach o współrzędnych:-2,0, 5,0. Na wykresie zaznaczono przedział -2,5. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź: $x \in ⟨- 2, 5⟩$ .

Przykład 8

Rozwiążemy nierówność $- 3 x^{2} + 2 x + 21 ⩽ 0$ .

Przekształcamy daną nierówność. Po pomnożeniu obustronnie przez $(- 1)$ otrzymujemy równoważnie

3 x^{2} - 2 x - 21 ⩾ 0

Rozpatrzmy funkcję kwadratową określoną wzorem $f (x) = 3 x^{2} - 2 x - 21$ . Ponieważ $a = 3 > 0$ , więc wykresem tej funkcji jest parabola, której ramiona skierowane są do góry.

Obliczamy wyróżnik: $Δ = {(- 2)}^{2} - 4 \cdot 3 \cdot (- 21) = 256 > 0$ . Zatem funkcja $f (x) = 3 x^{2} - 2 x - 21$ ma dwa miejsca zerowe:

$x_{1} = \frac{2 - \sqrt{256}}{2 \cdot 3} = - \frac{7}{3}$ oraz $x_{2} = \frac{2 + \sqrt{256}}{2 \cdot 3} = 3$ .

Sporządzamy szkic wykresu tej funkcji i na jego podstawie wyznaczamy argumenty, dla których $3 x^{2} - 2 x - 21 ⩾ 0$ .

RS7nqsmiQcIKf1

Wykres funkcji f(x) =3 x kwadrat -2x -21 z zaznaczonym rozwiązaniem nierówności. Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 28 do 28 oraz pionową osią Y od minus 20 do 8. Na płaszczyźnie narysowano parabolę z ramionami skierowanymi w górę. Parabola przecina poziomą oś w punktach o współrzędnych:-213,0, 3,0. Na wykresie zaznaczono przedział -∞,-213∪3,+∞. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź: $x \in (- \infty, - 2 \frac{1}{3}⟩ \cup ⟨3, + \infty)$ .

Przykład 9

Uzasadnimy, że dla dowolnej liczby rzeczywistej $x$ prawdziwa jest poniższa nierówność.

$x^{2} + 9 ⩾ 6 x$

sposób $I$

Przekształcamy nierówność w sposób równoważny do postaci $x^{2} - 6 x + 9 ⩾ 0$ . Wystarczy zatem pokazać, że funkcja kwadratowa $y = x^{2} - 6 x + 9$ przyjmuje wyłącznie wartości nieujemne.

Obliczamy wyróżnik trójmianu $y = x^{2} - 6 x + 9$ :

Δ = {(- 6)}^{2} - 4 \cdot 1 \cdot 9 = 0

Wynika stąd, że funkcja $y = x^{2} - 6 x + 9$ ma dokładnie jedno miejsce zerowe. Ponieważ jej wykresem jest parabola o ramionach skierowanych do góry ( $a = 1 > 0$ ), więc dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność $x^{2} - 6 x + 9 ⩾ 0$ . To kończy dowód.

sposób $II$

Przekształcamy nierówność w sposób równoważny.

x^{2} + 9 ⩾ 6 x

x^{2} - 6 x + 9 ⩾ 0

{(x - 3)}^{2} ⩾ 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(x - 3)}^{2} ⩾ 0$ . To spostrzeżenie kończy dowód.

$\frac{x^{2}}{7} + \frac{7}{4} ⩾ x$

sposób $I$

Przekształcamy nierówność w sposób równoważny do postaci $\frac{x^{2}}{7} - x + \frac{7}{4} ⩾ 0$ . Wystarczy pokazać, że funkcja kwadratowa $y = \frac{x^{2}}{7} - x + \frac{7}{4}$ przyjmuje wyłącznie wartości nieujemne.

Obliczamy wyróżnik trójmianu $y = \frac{x^{2}}{7} - x + \frac{7}{4}$

Δ = {(- 1)}^{2} - 4 \cdot \frac{1}{7} \cdot \frac{7}{4} = 0

Zatem funkcja ta ma dokładnie jedno miejsce zerowe, a ponieważ jej wykresem jest parabola o ramionach skierowanych do góry $(a = \frac{1}{7} > 0)$ , więc dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność $\frac{x^{2}}{7} - x + \frac{7}{4} ⩾ 0$ . To kończy dowód.

sposób $II$

Przekształcamy nierówność w sposób równoważny.

\frac{x^{2}}{7} + \frac{7}{4} ⩾ x

4 x^{2} + 49 ⩾ 28 x

4 x^{2} - 28 x + 49 ⩾ 0

{(2 x - 7)}^{2} ⩾ 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(2 x - 7)}^{2} ⩾ 0$ . To spostrzeżenie kończy dowód.

$3 (x^{2} + 3) > 10 x$

sposób $I$

Przekształcamy nierówność w sposób równoważny do postaci $3 x^{2} - 10 x + 9 > 0$ . Wystarczy pokazać, że funkcja kwadratowa $y = 3 x^{2} - 10 x + 9$ przyjmuje wyłącznie wartości dodatnie.

Ponieważ współczynnik przy $x^{2}$ trójmianu $y = 3 x^{2} - 10 x + 9$ jest dodatni, więc wykresem tej funkcji jest parabola o ramionach skierowanych do góry.

Obliczamy wyróżnik trójmianu $y = 3 x^{2} - 10 x + 9$

Δ = {(- 10)}^{2} - 4 \cdot 3 \cdot 9 = - 8 < 0

Zatem funkcja ta nie ma miejsc zerowych.

Wobec tego dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność $3 x^{2} - 10 x + 9 > 0$ . To kończy dowód.

sposób $II$

Przekształcamy nierówność w sposób równoważny.

3 (x^{2} + 3) > 10 x

3 x^{2} + 9 > 10 x

3 x^{2} - 10 x + 9 > 0

9 x^{2} - 30 x + 27 > 0

{(3 x - 5)}^{2} + 2 > 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(3 x - 5)}^{2} ⩾ 0$ , więc suma ${(3 x - 5)}^{2} + 2$ jest liczbą dodatnią. To spostrzeżenie kończy dowód.

Przykład 10

Uzasadnimy, że jeśli liczby $x$ i $y$ są rzeczywiste, to

$4 x^{2} + 25 y^{2} ⩾ 20 x y$

sposób $I$

Przekształcamy nierówność w sposób równoważny.

4 x^{2} - 20 x y + 25 y^{2} ⩾ 0

{(2 x - 5 y)}^{2} ⩾ 0

Jeżeli liczby $x$ i $y$ są rzeczywiste, to prawdziwa jest nierówność ${(2 x - 5 y)}^{2} ⩾ 0$ . To spostrzeżenie kończy dowód.

sposób $II$

Przekształcamy nierówność w sposób równoważny do postaci $4 x^{2} - 20 x y + 25 y^{2} ⩾ 0$ .

Możemy tę nierówność potraktować jako nierówność kwadratową z niewiadomą $x$ i dowolnie ustaloną liczbę $y$ .

Rozpatrzmy trójmian kwadratowy

f (x) = 4 x^{2} - 20 y \cdot x + 25 y^{2}

Trójmian ten ma dodatni współczynnik przy $x^{2}$ $(a = 4)$ .

Obliczamy wyróżnik tego trójmianu

$Δ = {(- 20 y)}^{2} - 4 \cdot 4 \cdot 25 y^{2} = 0$ . Zatem trójmian $f$ ma dokładnie jedno miejsce zerowe. Oznacza to, że dla każdego $x$ i dla każdego $y$ wartość tego trójmianu jest nieujemna. To spostrzeżenie kończy dowód.

$5 x^{2} + y^{2} + 4 x y ⩾ 2 x - 1$

sposób $I$

Przekształcamy nierówność w sposób równoważny.

5 x^{2} + y^{2} + 4 x y ⩾ 2 x - 1

5 x^{2} + y^{2} + 4 x y - 2 x + 1 ⩾ 0

4 x^{2} + 4 x y + y^{2} + x^{2} - 2 x + 1 ⩾ 0

{(2 x + y)}^{2} + {(x - 1)}^{2} ⩾ 0

Dla dowolnych liczb rzeczywistych $x$ i $y$ prawdziwa jest każda z nierówności ${(2 x + y)}^{2} ⩾ 0$ oraz ${(x - 1)}^{2} ⩾ 0$ , a zatem również prawdziwa jest nierówność ${(2 x + y)}^{2} + {(x - 1)}^{2} ⩾ 0$ . To spostrzeżenie kończy dowód.

sposób $II$

Zapiszmy nierówność w postaci równoważnej.

5 x^{2} + y^{2} + 4 x y - 2 x + 1 ⩾ 0

Rozpatrzmy trójmian kwadratowy.

f (x) = 5 x^{2} + (4 y - 2) x + (y^{2} + 1)

Trójmian ten ma dodatni współczynnik przy $x^{2}$ ( $a = 5$ ).
Obliczamy wyróżnik tego trójmianu

Δ = {(4 y - 2)}^{2} - 4 \cdot 5 \cdot (y^{2} + 1) = 16 y^{2} - 16 y + 4 - 20 y^{2} - 20 =

= - 4 (y^{2} + 4 y + 4) = - 4 {(y + 2)}^{2}

Dla każdego $y$ wyróżnik jest więc niedodatni, co oznacza, że funkcja może mieć co najwyżej jedno miejsce zerowe.

Zatem dla każdego $x$ i dla każdego $y$ wartość tego trójmianu jest nieujemna. To spostrzeżenie kończy dowód.

Przykład 11

Wykażemy, że jeśli $a ⩾ 0$ i $b ⩾ 0$ , to $\frac{a + b}{2} ⩾ \sqrt{a b}$ .

Przekształcamy nierówność w sposób równoważny.

\frac{a + b}{2} ⩾ \sqrt{a b}

a + b ⩾ 2 \sqrt{a b}

a - 2 \sqrt{a b} + b ⩾ 0

{(\sqrt{a})}^{2} - 2 \cdot \sqrt{a} \cdot \sqrt{b} + {(\sqrt{b})}^{2} ⩾ 0

{(\sqrt{a} - \sqrt{b})}^{2} ⩾ 0

Dla każdych liczb nieujemnych $a$ i $b$ nierówność ${(\sqrt{a} - \sqrt{b})}^{2} ⩾ 0$ jest prawdziwa. To spostrzeżenie kończy dowód.

Wykażemy, że jeśli $a > 0$ i $b > 0$ , to $\sqrt{a b} ⩾ \frac{2 a b}{a + b}$

Przekształcamy nierówność w sposób równoważny.

\sqrt{a b} ⩾ \frac{2 a b}{a + b}

a + b ⩾ \frac{2 a b}{\sqrt{a b}}

\frac{a + b}{2} ⩾ \frac{{(\sqrt{a b})}^{2}}{\sqrt{a b}}

\frac{a + b}{2} ⩾ \sqrt{a b}

Nierówność $\frac{a + b}{2} ⩾ \sqrt{a b}$ jest prawdziwa dla dowolnych liczb dodatnich $a$ i $b$ (co udowodniliśmy w poprzednim podpunkcie), co kończy dowód.

Uwaga. Dla liczb nieujemnych $a$ i $b$ liczbę $\frac{a + b}{2}$ nazywamy ich średnią arytmetyczną.

Dla liczb nieujemnych $a$ i $b$ liczbę $\sqrt{a b}$ nazywamy ich średnią geometryczną.

Dla liczb dodatnich $a$ i $b$ liczbę $\frac{2 a b}{a + b}$ (zapisywaną również w postaci $\frac{2}{\frac{1}{a} + \frac{1}{b}}$ ) nazywamy ich średnią harmoniczną.

R1DXC27VccQQe2

Ćwiczenie 1

$2 x^{2} > x$
$x^{2} > - 2$
$- 2 x^{2} < 1$
$- x^{2} < - 2$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RZwSBx3tQZR2v2

Ćwiczenie 2

$1$
$- 2$
${(- \frac{4}{3})}^{2}$
$- \sqrt{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rpzf2qJ6Ot48r2

Ćwiczenie 3

Zbiorem rozwiązań nierówności $(x + 3) (x + 5) < 0$ są liczby należące do przedziału $(3, 5)$ .
Zbiorem rozwiązań nierówności $(x + 2) (4 - x) > 0$ są liczby należące do przedziału $(- 2, 4)$ .
Zbiorem rozwiązań nierówności $x^{2} < 7$ są liczby należące do przedziału $(- 7, 7)$ .
Zbiorem rozwiązań nierówności $x^{2} < x$ są liczby należące do przedziału $(0, 1)$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rf9RQa0etYHFR1

Ćwiczenie 4

jest liczba $0$
nie ma żadnej liczby ujemnej
nie ma żadnej liczby dodatniej
jest dokładnie $7$ liczb całkowitych

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rkz3jLYrSOjp92

Ćwiczenie 5

$x^{2} + 5 x + 4 < 0$
$x^{2} + 4 x - 21 < 0$
$x^{2} - 9 x + 20 \leq 0$
$6 x^{2} - 13 x - 8 \leq 0$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RM5fIoLYvpFZa2

Ćwiczenie 6

$x^{2} - 36 < 0$
$x^{2} - 25 < 0$
$x^{2} - 16 < 0$
$x^{2} - 9 < 0$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RZs6jiy1rjWE91

Ćwiczenie 7

$- 2$
$5$
$1$
$3$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 8

RdkhcUM4xIWMN

RY83TYXDjLcDE1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R4dnCHFdR1lW61

Ćwiczenie 9

$k = - 4$
$k = - 2$
$k = 2$
$k = 4$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RrFGUWt45ggXj1

Ćwiczenie 10

$(0, 9)$
$(- 9, 0)$
$(- 3, 0)$
$(- 3, 3)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RvpnIu0ojyRsK1

Ćwiczenie 11

$- 2$
$- 1$
$0$
$1$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1jcPnGxO99qD1

Ćwiczenie 12

$(- 16, + \infty)$
$(4, + \infty)$
$(- \infty, 8) \cup (8, + \infty)$
$(- \infty, - 4) \cup (4, + \infty)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RqX939NobxrNy1

Ćwiczenie 13

$\frac{1}{4}$
$0$
$\frac{1}{2}$
$1$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R11X0imzD0ky81

Ćwiczenie 14

$f (x) > 0$
$g (x) < 0$
$f (x) > g (x)$
$f (x) < g (x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

iFwzWacLch_d5e1321

Ćwiczenie 15

R1EEPWrBDFeHh

Rozwiąż nierówność. Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłową odpowiedź.

(x + 1) (x - 2) < 0

x \in (- 2, 3)

, 2.

x \in (- \infty, - 2 \frac{1}{2}⟩ \cup ⟨4, + \infty)

, 3.

x \in (- \infty, 2) \cup (2, + \infty)

, 4.

x \in (- \infty, 3) \cup (3, + \infty)

, 5.

x \in (- \infty, - 2 \frac{3}{4}⟩ \cup ⟨5, + \infty)

, 6.

x \in (- 1, 2)

, 7.

x \in ⟨- \frac{1}{2}, 3⟩

, 8.

x \in ⟨- \frac{1}{3}, 4⟩

(x - 5) (4 x + 11) ⩾ 0

x \in (- 2, 3)

, 2.

x \in (- \infty, - 2 \frac{1}{2}⟩ \cup ⟨4, + \infty)

, 3.

x \in (- \infty, 2) \cup (2, + \infty)

, 4.

x \in (- \infty, 3) \cup (3, + \infty)

, 5.

x \in (- \infty, - 2 \frac{3}{4}⟩ \cup ⟨5, + \infty)

, 6.

x \in (- 1, 2)

, 7.

x \in ⟨- \frac{1}{2}, 3⟩

, 8.

x \in ⟨- \frac{1}{3}, 4⟩

(x - 2) (6 - 3 x) < 0

x \in (- 2, 3)

, 2.

x \in (- \infty, - 2 \frac{1}{2}⟩ \cup ⟨4, + \infty)

, 3.

x \in (- \infty, 2) \cup (2, + \infty)

, 4.

x \in (- \infty, 3) \cup (3, + \infty)

, 5.

x \in (- \infty, - 2 \frac{3}{4}⟩ \cup ⟨5, + \infty)

, 6.

x \in (- 1, 2)

, 7.

x \in ⟨- \frac{1}{2}, 3⟩

, 8.

x \in ⟨- \frac{1}{3}, 4⟩

(3 - x) (2 x + 1) ⩾ 0

x \in (- 2, 3)

, 2.

x \in (- \infty, - 2 \frac{1}{2}⟩ \cup ⟨4, + \infty)

, 3.

x \in (- \infty, 2) \cup (2, + \infty)

, 4.

x \in (- \infty, 3) \cup (3, + \infty)

, 5.

x \in (- \infty, - 2 \frac{3}{4}⟩ \cup ⟨5, + \infty)

, 6.

x \in (- 1, 2)

, 7.

x \in ⟨- \frac{1}{2}, 3⟩

, 8.

x \in ⟨- \frac{1}{3}, 4⟩

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

R170vY0uCGeMY

Rozwiąż nierówność. Kliknij w lukę, aby wyświetlić listę rozwijalną, i wybierz prawidłową odpowiedź.

x^{2} ⩽ 25

x \in (- \infty, 0) \cup (8, + \infty)

, 2.

x \in (- \sqrt{5}, \sqrt{5})

, 3.

x \in (- \infty, - \frac{3}{2}⟩ \cup ⟨0, + \infty)

, 4.

x \in (- \infty, - \frac{5}{2}⟩ \cup ⟨1, + \infty)

, 5.

x \in ⟨- 5, 6⟩

, 6.

x \in ⟨- 5, 5⟩

, 7.

x \in (- \sqrt{3}, \sqrt{3})

, 8.

x \in (- \infty, 0) \cup (4, + \infty)

8 x < x^{2}

x \in (- \infty, 0) \cup (8, + \infty)

, 2.

x \in (- \sqrt{5}, \sqrt{5})

, 3.

x \in (- \infty, - \frac{3}{2}⟩ \cup ⟨0, + \infty)

, 4.

x \in (- \infty, - \frac{5}{2}⟩ \cup ⟨1, + \infty)

, 5.

x \in ⟨- 5, 6⟩

, 6.

x \in ⟨- 5, 5⟩

, 7.

x \in (- \sqrt{3}, \sqrt{3})

, 8.

x \in (- \infty, 0) \cup (4, + \infty)

3 x + 2 x^{2} ⩾ 0

x \in (- \infty, 0) \cup (8, + \infty)

, 2.

x \in (- \sqrt{5}, \sqrt{5})

, 3.

x \in (- \infty, - \frac{3}{2}⟩ \cup ⟨0, + \infty)

, 4.

x \in (- \infty, - \frac{5}{2}⟩ \cup ⟨1, + \infty)

, 5.

x \in ⟨- 5, 6⟩

, 6.

x \in ⟨- 5, 5⟩

, 7.

x \in (- \sqrt{3}, \sqrt{3})

, 8.

x \in (- \infty, 0) \cup (4, + \infty)

9 - 3 x^{2} > 0

x \in (- \infty, 0) \cup (8, + \infty)

, 2.

x \in (- \sqrt{5}, \sqrt{5})

, 3.

x \in (- \infty, - \frac{3}{2}⟩ \cup ⟨0, + \infty)

, 4.

x \in (- \infty, - \frac{5}{2}⟩ \cup ⟨1, + \infty)

, 5.

x \in ⟨- 5, 6⟩

, 6.

x \in ⟨- 5, 5⟩

, 7.

x \in (- \sqrt{3}, \sqrt{3})

, 8.

x \in (- \infty, 0) \cup (4, + \infty)

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 17

R18vPKmKZM3l9

Rozwiąż nierówność.

x^{2} - 18 x + 81 > 0

Możliwe odpowiedzi: 1.

x \in (- \infty, 9) \cup (9, + \infty)

, 2.

x = 3

, 3. każda liczba rzeczywista

x

spełnia tę nierówność, 4. nierówność nie ma rozwiązań rzeczywistych

3 x^{2} - 18 x + 27 \leq 0

Możliwe odpowiedzi: 1.

x \in (- \infty, 9) \cup (9, + \infty)

, 2.

x = 3

, 3. każda liczba rzeczywista

x

spełnia tę nierówność, 4. nierówność nie ma rozwiązań rzeczywistych

x^{2} - 2 x + 3 < 0

Możliwe odpowiedzi: 1.

x \in (- \infty, 9) \cup (9, + \infty)

, 2.

x = 3

, 3. każda liczba rzeczywista

x

spełnia tę nierówność, 4. nierówność nie ma rozwiązań rzeczywistych

x^{2} - 6 x + 10 > 0

Możliwe odpowiedzi: 1.

x \in (- \infty, 9) \cup (9, + \infty)

, 2.

x = 3

, 3. każda liczba rzeczywista

x

spełnia tę nierówność, 4. nierówność nie ma rozwiązań rzeczywistych

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 18

RHUVoTvGLYRzK

Rozwiąż nierówność. Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłową odpowiedź.

x^{2} + 2 x - 24 < 0

x \in (- \infty, - 5) \cup (6, + \infty)

, 2.

x \in (- 8, 6)

, 3.

x \in (- 6, 4)

, 4.

x \in (- \infty, - 6⟩ \cup ⟨4, + \infty)

, 5.

x \in (- \infty, - 3) \cup (8, + \infty)

, 6.

x \in ⟨- 4, 8⟩

, 7.

x \in (- \infty, - 9⟩ \cup ⟨2, + \infty)

, 8.

x \in ⟨- 2, 6⟩

x^{2} - 5 x - 24 > 0

x \in (- \infty, - 5) \cup (6, + \infty)

, 2.

x \in (- 8, 6)

, 3.

x \in (- 6, 4)

, 4.

x \in (- \infty, - 6⟩ \cup ⟨4, + \infty)

, 5.

x \in (- \infty, - 3) \cup (8, + \infty)

, 6.

x \in ⟨- 4, 8⟩

, 7.

x \in (- \infty, - 9⟩ \cup ⟨2, + \infty)

, 8.

x \in ⟨- 2, 6⟩

- x^{2} + 4 x + 32 ⩾ 0

x \in (- \infty, - 5) \cup (6, + \infty)

, 2.

x \in (- 8, 6)

, 3.

x \in (- 6, 4)

, 4.

x \in (- \infty, - 6⟩ \cup ⟨4, + \infty)

, 5.

x \in (- \infty, - 3) \cup (8, + \infty)

, 6.

x \in ⟨- 4, 8⟩

, 7.

x \in (- \infty, - 9⟩ \cup ⟨2, + \infty)

, 8.

x \in ⟨- 2, 6⟩

- x^{2} - 7 x + 18 ⩽ 0

x \in (- \infty, - 5) \cup (6, + \infty)

, 2.

x \in (- 8, 6)

, 3.

x \in (- 6, 4)

, 4.

x \in (- \infty, - 6⟩ \cup ⟨4, + \infty)

, 5.

x \in (- \infty, - 3) \cup (8, + \infty)

, 6.

x \in ⟨- 4, 8⟩

, 7.

x \in (- \infty, - 9⟩ \cup ⟨2, + \infty)

, 8.

x \in ⟨- 2, 6⟩

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 19

RnLpevI8mKAGD

Rozwiąż nierówność. Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłową odpowiedź.

2 x^{2} + 7 x - 4 ⩽ 0

x \in ⟨- 4, \frac{1}{2}⟩

, 2.

x \in (- 4, - 1 \frac{1}{3})

, 3.

x \in ⟨- 2, \frac{1}{2}⟩

, 4.

x \in (- \infty, - 8⟩ \cup ⟨\frac{1}{3}, + \infty)

, 5.

x \in (- 2, - 1 \frac{1}{3})

, 6.

x \in (- \infty, - 6⟩ \cup ⟨\frac{2}{3}, + \infty)

, 7.

x \in (- \infty, - 4 \frac{1}{4}) \cup (- 6, + \infty)

, 8.

x \in (- \infty, - 4 \frac{1}{2}) \cup (- 3, + \infty)

3 x^{2} + 10 x + 8 < 0

x \in ⟨- 4, \frac{1}{2}⟩

, 2.

x \in (- 4, - 1 \frac{1}{3})

, 3.

x \in ⟨- 2, \frac{1}{2}⟩

, 4.

x \in (- \infty, - 8⟩ \cup ⟨\frac{1}{3}, + \infty)

, 5.

x \in (- 2, - 1 \frac{1}{3})

, 6.

x \in (- \infty, - 6⟩ \cup ⟨\frac{2}{3}, + \infty)

, 7.

x \in (- \infty, - 4 \frac{1}{4}) \cup (- 6, + \infty)

, 8.

x \in (- \infty, - 4 \frac{1}{2}) \cup (- 3, + \infty)

- 2 x^{2} - 15 x - 27 < 0

x \in ⟨- 4, \frac{1}{2}⟩

, 2.

x \in (- 4, - 1 \frac{1}{3})

, 3.

x \in ⟨- 2, \frac{1}{2}⟩

, 4.

x \in (- \infty, - 8⟩ \cup ⟨\frac{1}{3}, + \infty)

, 5.

x \in (- 2, - 1 \frac{1}{3})

, 6.

x \in (- \infty, - 6⟩ \cup ⟨\frac{2}{3}, + \infty)

, 7.

x \in (- \infty, - 4 \frac{1}{4}) \cup (- 6, + \infty)

, 8.

x \in (- \infty, - 4 \frac{1}{2}) \cup (- 3, + \infty)

- 3 x^{2} - 23 x + 8 ⩽ 0

x \in ⟨- 4, \frac{1}{2}⟩

, 2.

x \in (- 4, - 1 \frac{1}{3})

, 3.

x \in ⟨- 2, \frac{1}{2}⟩

, 4.

x \in (- \infty, - 8⟩ \cup ⟨\frac{1}{3}, + \infty)

, 5.

x \in (- 2, - 1 \frac{1}{3})

, 6.

x \in (- \infty, - 6⟩ \cup ⟨\frac{2}{3}, + \infty)

, 7.

x \in (- \infty, - 4 \frac{1}{4}) \cup (- 6, + \infty)

, 8.

x \in (- \infty, - 4 \frac{1}{2}) \cup (- 3, + \infty)

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

R1JWBFY0Lqjmj

Rozwiąż nierówność. Kliknij w lukę, aby wyświetlić listę rozwijalną, i wybierz prawidłową odpowiedź.

4 x^{2} - 8 x - 45 > 0

x \in (- \infty, - 4 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 2.

x \in (- \infty, \frac{1}{4}) \cup (6, + \infty)

, 3.

x \in ⟨- \frac{5}{6}, 2⟩

, 4.

x \in ⟨- \frac{5}{8}, 2⟩

, 5.

x \in (- \infty, - \frac{2}{5}⟩ \cup ⟨\frac{1}{5}, + \infty)

, 6.

x \in (- \infty, \frac{1}{6}) \cup (6, + \infty)

, 7.

x \in (- \infty, - 2 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 8.

x \in (- \infty, - \frac{2}{3}⟩ \cup ⟨\frac{1}{5}, + \infty)

15 x^{2} + 7 x - 2 ⩾ 0

x \in (- \infty, - 4 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 2.

x \in (- \infty, \frac{1}{4}) \cup (6, + \infty)

, 3.

x \in ⟨- \frac{5}{6}, 2⟩

, 4.

x \in ⟨- \frac{5}{8}, 2⟩

, 5.

x \in (- \infty, - \frac{2}{5}⟩ \cup ⟨\frac{1}{5}, + \infty)

, 6.

x \in (- \infty, \frac{1}{6}) \cup (6, + \infty)

, 7.

x \in (- \infty, - 2 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 8.

x \in (- \infty, - \frac{2}{3}⟩ \cup ⟨\frac{1}{5}, + \infty)

- 4 x^{2} + 25 x - 6 < 0

x \in (- \infty, - 4 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 2.

x \in (- \infty, \frac{1}{4}) \cup (6, + \infty)

, 3.

x \in ⟨- \frac{5}{6}, 2⟩

, 4.

x \in ⟨- \frac{5}{8}, 2⟩

, 5.

x \in (- \infty, - \frac{2}{5}⟩ \cup ⟨\frac{1}{5}, + \infty)

, 6.

x \in (- \infty, \frac{1}{6}) \cup (6, + \infty)

, 7.

x \in (- \infty, - 2 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 8.

x \in (- \infty, - \frac{2}{3}⟩ \cup ⟨\frac{1}{5}, + \infty)

- 6 x^{2} + 7 x + 10 ⩾ 0

x \in (- \infty, - 4 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 2.

x \in (- \infty, \frac{1}{4}) \cup (6, + \infty)

, 3.

x \in ⟨- \frac{5}{6}, 2⟩

, 4.

x \in ⟨- \frac{5}{8}, 2⟩

, 5.

x \in (- \infty, - \frac{2}{5}⟩ \cup ⟨\frac{1}{5}, + \infty)

, 6.

x \in (- \infty, \frac{1}{6}) \cup (6, + \infty)

, 7.

x \in (- \infty, - 2 \frac{1}{2}) \cup (4 \frac{1}{2}, + \infty)

, 8.

x \in (- \infty, - \frac{2}{3}⟩ \cup ⟨\frac{1}{5}, + \infty)

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 21

Rozwiąż nierówność $- 3 x^{2} + 2 x + 5 ⩾ 0$ i wypisz wszystkie liczby całkowite, które ją spełniają.

ROaDVXp7qGOH6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$x \in \{- 1, 0, 1\}$ .

Ćwiczenie 22

Wyznacz zbiór wszystkich liczb rzeczywistych, które spełniają jednocześnie nierówności $5 x^{2} + 7 x - 24 ⩾ 0$ i $x < 2$ .

Ryk6UeELrdkix

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Na początku wyznacz zbiór rozwiązań nierówności $5 x^{2} + 7 x - 24 ⩾ 0$ . Następnie z otrzymanego rozwiązania wyznacz te argumenty, które są mniejsze niż $2$ .

$x \in (- \infty, - 3⟩ \cup ⟨1 \frac{3}{5}, 2)$ .

Ćwiczenie 23

Uzasadnij, że jeżeli $x$ jest dowolną liczbą rzeczywistą, to prawdziwa jest nierówność $25 x^{2} + 36 ⩾ 60 x$ .

RIZzlGjdpcDQ5

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekształcamy nierówność w sposób równoważny.

25 x^{2} + 36 ⩾ 60 x

25 x^{2} - 60 x + 36 ⩾ 0

{(5 x - 6)}^{2} ⩾ 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(5 x - 6)}^{2} ⩾ 0$ , gdyż kwadrat każdej liczby rzeczywistej jest nieujemny.

Ćwiczenie 24

Uzasadnij, że jeżeli $x$ jest dowolną liczbą rzeczywistą, to prawdziwa jest nierówność $\frac{3 x^{2}}{10} + \frac{5}{6} ⩾ x$ .

Rx0QXIjXNnMtf

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekształcamy nierówność w sposób równoważny.

\frac{3 x^{2}}{10} + \frac{5}{6} ⩾ x

9 x^{2} + 25 ⩾ 30 x

9 x^{2} - 30 x + 25 ⩾ 0

{(3 x - 5)}^{2} ⩾ 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(3 x - 5)}^{2} ⩾ 0$ .

Ćwiczenie 25

Uzasadnij, że jeżeli $x$ jest dowolną liczbą rzeczywistą, to prawdziwa jest nierówność $2 x^{2} + 11 > 9 x$ .

RI6Dqs1odrnbC

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pokaż, że trójmian kwadratowy $y = 2 x^{2} - 9 x + 11$ przyjmuje wyłącznie wartości dodatnie.

Przekształcamy nierówność w sposób równoważny do postaci $2 x^{2} - 9 x + 11 > 0$ .

Wystarczy więc pokazać, że trójmian kwadratowy $y = 2 x^{2} - 9 x + 11$ przyjmuje wyłącznie wartości dodatnie.

Ponieważ współczynnik przy $x^{2}$ tego trójmianu jest dodatni, więc wykresem tego trójmianu jest parabola o ramionach skierowanych do góry.

Obliczamy wyróżnik trójmianu

Δ = {(- 9)}^{2} - 4 \cdot 2 \cdot 11 = 81 - 88 = - 7 < 0

Zatem trójmian nie ma miejsc zerowych. Trójmian kwadratowy $y = 2 x^{2} - 9 x + 11$ przyjmuje tylko dodatnie wartości.

Wobec tego dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność $2 x^{2} - 9 x + 11 > 0$ . To kończy dowód.

Ćwiczenie 26

Uzasadnij, że jeżeli $x$ jest dowolną liczbą rzeczywistą, to prawdziwa jest nierówność $5 (x^{2} + 2) > 14 x$ .

R376mpXSdY8qq

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pokaż, że nierówność $5 x^{2} - 14 x + 10 > 0$ przyjmuje tylko wartości dodatnie.

Przekształcamy nierówność w sposób równoważny.

5 x^{2} + 10 > 14 x

5 x^{2} - 14 x + 10 > 0

25 x^{2} - 70 x + 50 > 0

{(5 x - 7)}^{2} + 1 > 0

Dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność ${(5 x - 7)}^{2} ⩾ 0$ , więc suma ${(5 x - 7)}^{2} + 1$ jest liczbą dodatnią.

Ćwiczenie 27

Uzasadnij, że dla dowolnych liczb rzeczywistych $x$ i $y$ prawdziwa jest nierówność $49 x^{2} + 9 y^{2} ⩾ 42 x y$ .

R1Z4hMeIt6tVU

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekształcamy nierówność w sposób równoważny.

49 x^{2} - 42 x y + 9 y^{2} ⩾ 0

{(7 x - 3 y)}^{2} ⩾ 0

Otrzymana nierówność jest prawdziwa, gdyż kwadrat dowolnej liczby rzeczywistej jest nieujemny.

Ćwiczenie 28

Uzasadnij, że dla dowolnych liczb rzeczywistych $x$ i $y$ prawdziwa jest nierówność $2 x^{2} + y^{2} + 8 x + 16 ⩾ 2 x y$ .

R1ZQ7yR8sx9Rg

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekształcamy nierówność w sposób równoważny.

2 x^{2} + y^{2} + 8 x + 16 - 2 x y ⩾ 0

x^{2} + 8 x + 16 + y^{2} - 2 x y + x^{2} ⩾ 0

{(x + 4)}^{2} + {(y - x)}^{2} ⩾ 0

Jeżeli liczby $x$ i $y$ są rzeczywiste, to prawdziwa jest każda z nierówności ${(x + 4)}^{2} ⩾ 0$ oraz ${(y - x)}^{2} ⩾ 0$ , a zatem również prawdziwa jest nierówność ${(x + 4)}^{2} + {(y - x)}^{2} ⩾ 0$ . To kończy dowód.

Ćwiczenie 29

Uzasadnij, że dla dowolnych liczb rzeczywistych $x$ i $y$ prawdziwa jest nierówność $x^{2} + 10 y^{2} + 6 x y ⩾ 5 (2 y - 5)$ .

R9iNZpnjEULAz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekształcamy nierówność w sposób równoważny

x^{2} + 10 y^{2} + 6 x y ⩾ 10 y - 25

x^{2} + 10 y^{2} + 6 x y - 10 y + 25 ⩾ 0

x^{2} + 6 x y + 9 y^{2} + y^{2} - 10 y + 25 ⩾ 0

{(x + 3 y)}^{2} + {(y - 5)}^{2} ⩾ 0

Jeżeli liczby $x$ i $y$ są rzeczywiste, to prawdziwa jest każda z nierówności ${(x + 3 y)}^{2} ⩾ 0$ oraz ${(y - 5)}^{2} ⩾ 0$ , a zatem również prawdziwa jest nierówność ${(x + 3 y)}^{2} + {(y - 5)}^{2} ⩾ 0$ . To kończy dowód.

Ćwiczenie 30

Wykaż, że nierówność $\sqrt{\frac{a^{2} + b^{2}}{2}} ⩾ \frac{a + b}{2}$ jest spełniona przez wszystkie liczby rzeczywiste $a$ i $b$ .

RLRG7YaQAze8F

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

W przypadku, gdy $a < 0$ i $b < 0$ , prawa strona nierówności jest ujemna, lewa dodatnia – zatem nierówność jest spełniona.

Podobnie, gdy $b > a$ .

Dla $a > b$ obie strony nierówności są dodatnie. Po podniesieniu obu stron nierówności do kwadratu i przekształceniach otrzymujemy:

\frac{a^{2} + b^{2}}{2} ⩾ \frac{a^{2} + b^{2} + 2 a b}{4}

co po przekształceniach prowadzi do nierówności zawsze prawdziwej

{(a - b)}^{2} ⩾ 0