RxQGzjq6U5fbM

Rachunek prawdopodobieństwa to dział matematyki, który zajmuje się badaniem szans wystąpienia danego zjawiska. Do znacznego rozwoju tej dziedziny matematyki przyczynił się hazard. To właśnie z rozważań dotyczących gier losowych w $XVII$ wieku, rachunek prawdopodobieństwa został sformalizowany i potraktowany jako osobna dziedzina matematyki na początku $XX$ wieku.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Ilustracja interaktywnaIlustracja interaktywna
Gra edukacyjnaGra edukacyjna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Przeprowadzisz proste doświadczenie losowe.
Obliczysz prawdopodobieństwo prostego zdarzenia losowego.
Wykorzystasz zdobytą wiedzę do rozwiązywania problemów matematycznych.

Zapiszemy na początku definicję doświadczenia losowego.

doświadczenie losowe

Definicja: doświadczenie losowe

Zjawisko losowe, które można powtarzać wiele razy w tych samych warunkach, ale jego kolejnych wyników nie potrafimy przewidzieć nazywamy doświadczeniem losowym.

Doświadczeniami losowymidoświadczenie losoweDoświadczeniami losowymi mogą być np. rzut kostką do gry, rzut monetą, losowanie karty z talii. Z pojęciem tym związane jest zdarzenie elementarne, którego nie definiuje się (jest to tzw. pojęcie pierwotne w teorii prawdopodobieństwa). W przypadku doświadczenia polegającego na jednokrotnym rzucie kostką, możliwych jest sześć pojedynczych wyników - zdarzeń elementarnych: $1$ , $2$ , $3$ , $4$ , $5$ lub $6$ oczek, a w przypadku rzutu monetą - dwa zdarzenia elementarne: orzeł lub reszka. Po analizie doświadczenia losowego możemy wyznaczyć częstość występowania poszczególnych wyników. W ten sposób obliczamy prawdopodobieństwo zdarzenia.

prawdopodobieństwo zdarzenia

Definicja: prawdopodobieństwo zdarzenia

Prawdopodobieństwem zdarzenia nazywamy szansę na wystąpienie danego zdarzenia.

Jeżeli $n$ jest liczbą zdarzeń elementarnych sprzyjających danemu zdarzeniu, zaś $N$ – liczbą wszystkich zdarzeń elementarnych, to prawdopodobieństwo $p$ zdarzenia obliczamy ze wzoru:
$p = \frac{n}{N}$

Przykład 1

Rzucamy jeden raz symetryczną, sześcienną kostką do gry. Obliczymy, jakie jest prawdopodobieństwo tego, że otrzymamy liczbę oczek, która jest:

parzysta,
liczbą pierwszą,
liczbą podzielną przez $3$ .

Rozwiązanie:

Wypisujemy wszystkie możliwe wyniki rzutu sześcienną kostką do gry, jeżeli liczba oczek jest parzysta: $2$ , $4$ , $6$ oczek.
Wobec tego $n = 3$ .
Zatem prawdopodobieństwo tego, że w rzucie sześcienną kostką do gry wypadnie parzysta liczba oczek wynosi:
$p = \frac{3}{6} = \frac{1}{2}$ ,
Wypisujemy wszystkie możliwe wyniki rzutu sześcienną kostką do gry, jeżeli wyrzucona liczba oczek jest liczbą pierwszą: $2$ , $3$ lub $5$ oczek.
Wobec tego $n = 3$ .
Zatem prawdopodobieństwo tego, że w rzucie sześcienną kostką do gry wypadnie liczba oczek będąca liczbą pierwszą wynosi:
$p = \frac{3}{6} = \frac{1}{2}$ ,
Wypisujemy wszystkie możliwe wyniki rzutu sześcienną kostką do gry, jeżeli liczba oczek jest podzielna przez $3$ : $3$ lub $6$ oczek.
Wobec tego $n = 2$ .
Zatem prawdopodobieństwo tego, że w rzucie sześcienną kostką do gry wypadnie liczba oczek podzielna przez $3$ wynosi:
$p = \frac{2}{6} = \frac{1}{3}$ .

Przykład 2

W urnie znajduje się $28$ kul, w tym $12$ kul białych. Losujemy jedną kulę z urny. Obliczymy prawdopodobieństwo tego, że wylosowana kula nie jest biała.

Rozwiązanie:

Ponieważ wylosowana kula nie może być biała, zatem:
$n = 28 - 12 = 16$ ,
$N = 28$ .
Zatem prawdopodobieństwo $p$ zdarzenia polegającego na tym, że wylosowana kula nie jest biała wynosi:
$p = \frac{16}{28} = \frac{4}{7}$ .

Przykład 3

Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Obliczymy prawdopodobieństwo zdarzenia takiego, że wylosujemy liczbę będącą:

wielokrotnością liczby $7$ ,
podzielną przez $9$ .

Rozwiązanie:

Wszystkich liczb dwucyfrowych jest $90$ , zatem $N = 90$ .

Wypisujemy dwucyfrowe wielokrotności liczby $7$ :
$14$ , $21$ , $28$ , $35$ , $42$ , $49$ , $56$ , $63$ , $70$ , $77$ , $84$ , $91$ , $98$ .
Wobec tego:
$n = 13$ ,
$p = \frac{13}{90}$ ,
Wypisujemy liczby dwucyfrowe podzielne przez $9$ :
$18$ , $27$ , $36$ , $45$ , $54$ , $63$ , $72$ , $81$ , $90$ , $99$ .
Wobec tego:
$n = 10$ , $p = \frac{10}{90} = \frac{1}{9}$ .

Przykład 4

Rzucamy dwukrotnie symetryczną monetą. Obliczymy prawdopodobieństwo tego, że:

ani razu nie otrzymamy orła,
wypadnie co najmniej jeden orzeł.

Rozwiązanie:

Przedstawmy wszystkie możliwe wyniki doświadczenia za pomocą drzewa.

RznAIGDw32sEb

Źródło: GroMar Sp. z o. o., licencja: CC BY 3.0.

Ilustracja przedstawia drzewo ilustrujące możliwości wyrzucenia orła i reszki w dwóch kolejnych rzutach. Literą O oznaczono sytuację w której wyrzucono orła, natomiast litera R oznaczono sytuację w której wyrzucono reszkę. Z punktu wyjściowego nazwanego START mamy dwie odchodzące gałęzie. górna gałąź prowadzi do punktu z podpisem O pierwszy rzut, a dolna krawędź prowadzi do punktu z podpisem R pierwszy rzut. Od punktu O pierwszy rzut odchodzą dwie gałęzie, górna gałąź prowadzi do punktu O drugi rzut, a dolna krawędź prowadzi do punktu R drugi rzut. Od puntu R pierwszy rzut odchodzą dwie gałęzie, górna gałąź prowadzi do punktu O drugi rzut, a dolna krawędź prowadzi do punktu R drugi rzut.

Liczba wszystkich możliwych wyników doświadczenia wynosi $4$ .

Jeśli ani razu nie otrzymaliśmy orła, to oznacza, że otrzymujemy dwie reszki. Zatem:
$n = 1$ ,
$N = 4$ ,
$p = \frac{1}{4}$ ,
Jeśli wypadł co najmniej jeden orzeł, to oznacza, że wypadł dokładnie jeden orzeł lub wypadły dokładnie dwa orły. Zatem:
$n = 3$ ,
$N = 4$ ,
$p = \frac{3}{4}$ .

Przykład 5

Rzucamy dwukrotnie symetryczną, sześcienną kostką do gry. Obliczymy, jakie jest prawdopodobieństwo tego, że iloczyn wyrzuconych oczek jest podzielny przez $6$ .

Rozwiązanie:

Liczba wszystkich możliwych wyników tego doświadczenia wynosi $36$ , zatem $N = 36$ .

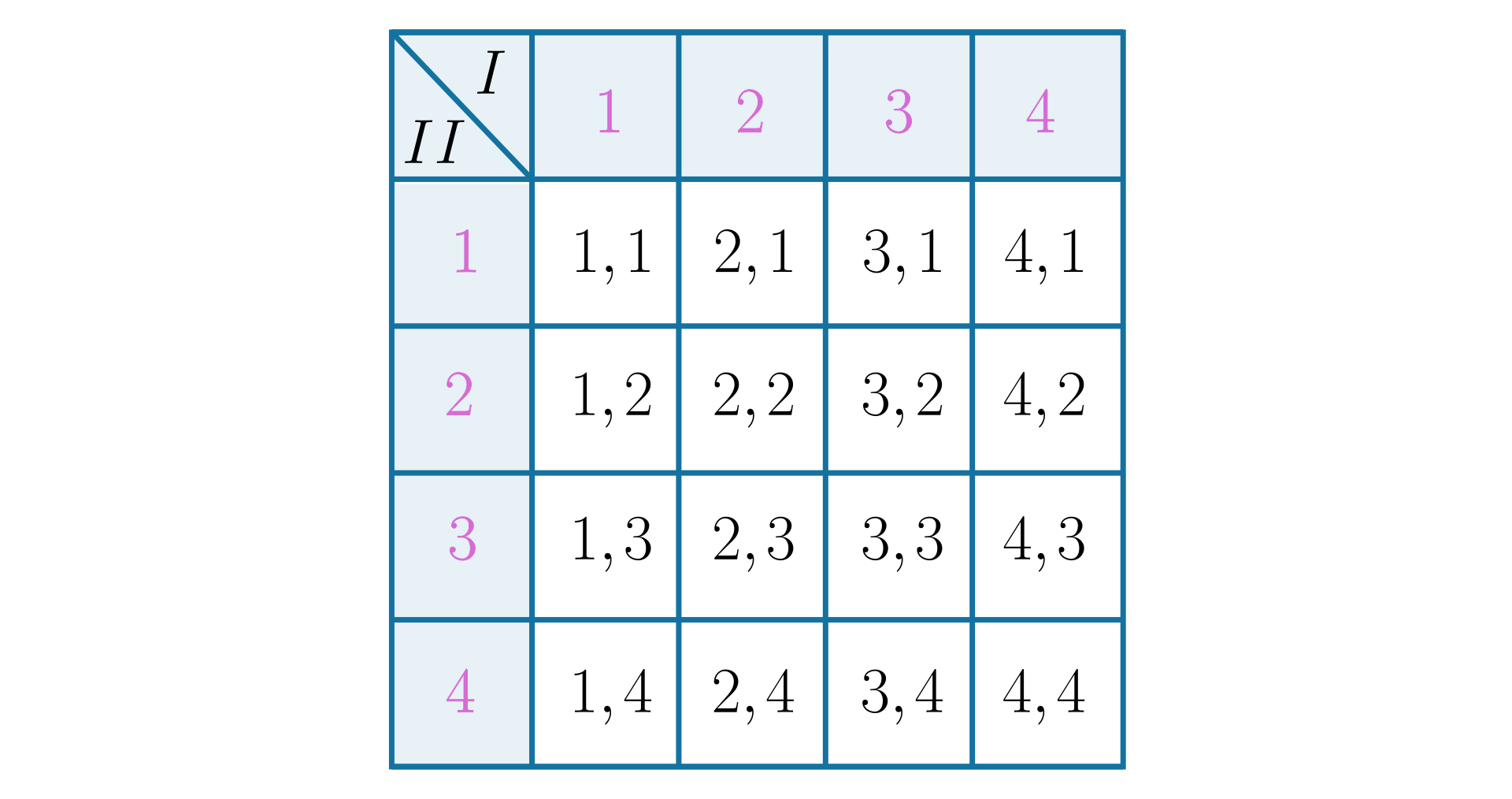
Przedstawmy za pomocą tabeli zbiór iloczynów liczb oczek, otrzymanych przy dwukrotnym rzucie symetryczną, sześcienną kostką do gry.

$\cdot$	$1$	$2$	$3$	$4$	$5$	$6$
$1$	$1$	$2$	$3$	$4$	$5$	$6$
$2$	$2$	$4$	$6$	$8$	$10$	$12$
$3$	$3$	$6$	$9$	$12$	$15$	$18$
$4$	$4$	$8$	$12$	$16$	$20$	$24$
$5$	$5$	$10$	$15$	$20$	$25$	$30$
$6$	$6$	$12$	$18$	$24$	$30$	$36$

Zaznaczmy w tabeli te liczby, które są podzielne przez $6$ :

$\cdot$	$1$	$2$	$3$	$4$	$5$	$6$
$1$	$1$	$2$	$3$	$4$	$5$	$6$
$2$	$2$	$4$	$6$	$8$	$10$	$12$
$3$	$3$	$6$	$9$	$12$	$15$	$18$
$4$	$4$	$8$	$12$	$16$	$20$	$24$
$5$	$5$	$10$	$15$	$20$	$25$	$30$
$6$	$6$	$12$	$18$	$24$	$30$	$36$

Zatem $n = 15$ .
Wobec tego prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn wyrzuconych oczek jest podzielny przez $6$ wynosi:
$p = \frac{15}{36} = \frac{5}{12}$

Przykład 6

Na loterii jest o $168$ więcej losów przegrywających niż wygrywających, łącznie jest $200$ losów. Wyciągamy jeden los. Obliczymy, jakie jest prawdopodobieństwo wygranej.

Rozwiązanie:

Wprowadźmy następujące oznaczenia:
$x$ – liczba losów wygrywających
$x + 168$ – liczba losów przegrywających

Wobec tego, do wyznaczenia liczby losów wygrywających rozwiązujemy równanie:
$x + x + 168 = 200$
$2 x + 168 = 200$
$2 x = 32$
$x = 16$
Zatem na loterii jest $16$ losów wygrywających.
Do wyznaczenia prawdopodobieństwa wygranej, wprowadzamy następujące oznaczenia:
$n = 16$ (liczba zdarzeń sprzyjających)
$N = 200$ (liczba wszystkich zdarzeń elementarnych)
$p = \frac{16}{200} = \frac{2}{25}$
Prawdopodobieństwo wygranej na loterii wynosi $\frac{2}{25}$ .

Notatki

R1amCxzlRixNn

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ilustracja interaktywna

R5pmGJcGZkBIx

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ze zbioru liczb naturalnych, które są większe od $100$ i nie większe niż $130$ losujemy jedna liczbę. Jakie jest pradopodobieństo zdarzenia że losujemy liczbę parzystą, która dodatkowego jest podzielna przez $3$ ?

Etap pierwszy:

Ustalmy liczbę wszystkich liczb naturalnych większych od stu i nie większych od stu trzydziestu. $101, 102, \dots, 128, 129, 130$ .

Jest $30$ liczb naturalnych, które są większe od $100$ i nie większe niż $130$ .

Etap drugi:

Ustalmy liczbę wszystkich liczb naturalnych większych od stu i nie większych od stu trzydziestu, które dodatkowo są parzyste i podzielne przez trzy.

$102, 108, 114, 120, 126$ .

Jest pięć liczb naturalnych, które spełniają założenia zadania i jednocześnie są parzyste i podzielne przez trzy.

Etap trzy:

Obliczamy prawdopodobieństwo zdarzenia korzystając z odpowiedniego wzoru. $p = \frac{5}{30} = \frac{1}{6}$ .

Prawdopodobieństwo zdarzenia, że wylosujemy liczbę parzysta i podzielna przez trzy ze zbioru liczb naturalnych niż $100$ i nie większych niż $130$ wynosi $\frac{1}{6}$ .

Polecenie 1

Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo zdarzenia, że wylosujemy liczbę podzielną przez $6$ ?

R1Q9vz0g90gbi

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Na początku oblicz, ile jest wszystkich liczb dwucyfrowych. Następnie wyznacz te, które spełniają założenia zadania. Pamiętaj, że liczba jest podzielna przez $6$ , gdy jest podzielna przez $2$ i przez $3$ .

Jest $90$ liczb dwucyfrowych.

Wśród wszystkich liczb dwucyfrowych jest $15$ liczb, które spełniają założenia zadania: $12, 18, 24, 30, 36, 42, 48, . . . ., 96$

Prawdopodobieństwo zdarzenia, że ze zbioru liczb dwucyfrowych wylosujemy liczbę podzielną przez $6$ wynosi: $p = \frac{15}{90} = \frac{1}{6}$ .

Polecenie 2

Ze zbioru liczb trzycyfrowych, podzielnych przez $5$ losujemy jedną liczbę. Jakie jest prawdopodobieństwo zdarzenia, że wylosowana liczba ma cyfrę setek równą $3$ ?

R1Q9vz0g90gbi

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Liczba jest podzielna przez $5$ , gdy cyfrą jej jedności jest $0$ lub $5$ .

Jest $900$ liczb trzycyfrowych.

Wśród wszystkich liczb trzycyfrowych jest $180$ liczb, które są podzielne przez $5$ : $100, 105, 110, . . . ., 995$ .

Wśród tych $180$ liczb jest $20$ liczb, których cyfrą setek jest $3$ : $300, 305, 310, . . ., 395$

Prawdopodobieństwo zdarzenia, że ze zbioru liczb trzycyfrowych podzielnych przez $5$ wylosujemy liczbę, której cyfra setek jest równa $3$ wynosi: $p = \frac{20}{180} = \frac{1}{9}$ .

Polecenie 3

Ze zbioru liczb dwucyfrowych, które przy dzieleniu przez $5$ dają resztę $3$ losujemy jedną liczbę. Jakie jest prawdopodobieństwo zdarzenia, że wylosowana liczba jest mniejsza niż $40$ ?

R1Q9vz0g90gbi

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Najmniejsza liczba dwucyfrowa, która przy dzieleniu przez $5$ daje resztę $3$ to $13$ , a największa $98$ .

Jest $18$ liczb naturalnych dwucyfrowych, które przy dzieleniu przez $5$ dają resztę $3$ : $13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83, 88, 93, 98$ .

Wśród tych liczb jest $6$ liczb, które są mniejsze niż $40$ : $13, 18, 23, 28, 33, 38$ .

Wobec tego prawdopodobieństwo zdarzenia, że wylosowana liczba jest mniejsza niż $40$ jest równe: $p = \frac{6}{18} = \frac{1}{3}$ .

Gra edukacyjna

Zagraj w grę, a następnie wykonaj poniższe polecenia.

R1NXcoYfOpWUG

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Gra edukacyjna - Obliczanie prawdopodobieństwa zdarzeń.60Brawo! Udało się się poprawnie rozwiązać test.Niestety nie udało Ci się poprawnie rozwiązać testu. Spróbuj jeszcze raz.1

Test

Gra edukacyjna - Obliczanie prawdopodobieństwa zdarzeń.

Gra składa się z trzech poziomów. Na każdym poziomie jest sześć pytań. W każdym pytaniu tylko jedna poprawna odpowiedź.

Liczba pytań:

Limit czasu:

min

Pozostało prób:

1/1

Twój ostatni wynik:

Gra edukacyjna - Obliczanie prawdopodobieństwa zdarzeń.

Pytanie 1/18

Twój ostatni wynik -

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Polecenie 4

Spośród liczb naturalnych od $1$ do $100$ losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia:

wylosowana liczba jest parzysta,
wylosowana liczba jest sześcianem liczby naturalnej,
wylosowana liczba przy dzieleniu przez $12$ daje resztę $9$ .

R1Q9vz0g90gbi

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zauważ, że liczba wszystkich zdarzeń elementarnych jest równa $100$ . Połowę z tych liczb stanowią liczby parzyste.

Zauważmy, że $N = 100$ .

Wśród liczb naturalnych od $1$ do $100$ jest $50$ liczb parzystych, zatem $n = 50$ .
Wobec tego:
$p = \frac{50}{100} = \frac{1}{2}$ ,
Wśród liczb naturalnych od $1$ do $100$ są $4$ liczby, będące sześcianem liczby naturalnej: $1$ , $8$ , $27$ , $64$ , zatem $n = 4$ .
Wobec tego:
$p = \frac{4}{100} = \frac{1}{25}$ ,
Wśród liczb naturalnych od $1$ do $100$ jest $8$ liczb, które przy dzieleniu przez $12$ dają resztę $9$ : $9$ , $21$ , $33$ , $45$ , $57$ , $69$ , $81$ , $93$ . Zatem $n = 8$ .
Wobec tego:
$p = \frac{8}{100} = \frac{2}{25}$ .

Polecenie 5

W klasie jest $25$ uczniów, w tym $11$ dziewcząt. Wybieramy losowo jedną osobę. Oblicz prawdopodobieństwo tego, że wybierzemy chłopca.

RatC3tDI2otGd

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zauważmy, że $N = 25$ .

Wyznaczamy liczbę chłopców w tej klasie: $25 - 11 = 14$

Zatem $n = 14$ .

Wobec tego:

$p = \frac{14}{25}$ .

Polecenie 6

R1DtI5Yc0y3g4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zestaw ćwiczeń interaktywnych

R1VVWbjvSxXpa

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

RcvKhVtRffDfs

Ćwiczenie 2

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Połącz w pary zdarzenie losowe z odpowiadającym mu prawdopodobieństwem. suma wyrzuconych oczek wynosi

10

Możliwe odpowiedzi: 1.

\frac{11}{36}

, 2.

\frac{1}{2}

, 3.

\frac{1}{3}

, 4.

\frac{1}{12}

iloczyn wyrzuconych oczek jest podzielny przez

5

Możliwe odpowiedzi: 1.

\frac{11}{36}

, 2.

\frac{1}{2}

, 3.

\frac{1}{3}

, 4.

\frac{1}{12}

za pierwszym razem wypadła liczba oczek nie większa niż

2

Możliwe odpowiedzi: 1.

\frac{11}{36}

, 2.

\frac{1}{2}

, 3.

\frac{1}{3}

, 4.

\frac{1}{12}

na drugiej kostce wypadła parzysta liczba oczek Możliwe odpowiedzi: 1.

\frac{11}{36}

, 2.

\frac{1}{2}

, 3.

\frac{1}{3}

, 4.

\frac{1}{12}

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

ROxnnD2ZJW1mK

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1E4epkKjROYJ

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

RGG2M7bE4b2sW

Ćwiczenie 5

Rzucamy trzy razy symetryczną monetą. Pogrupuj elementy zgodnie z podanym opisem. Zdarzenia, których prawdopodobieństwa wynoszą

\frac{1}{2}

: Możliwe odpowiedzi: 1. liczba wyrzuconych orłów jest mniejsza niż liczba wyrzuconych reszek, 2. za drugim razem otrzymano orła, 3. liczba wyrzuconych orłów jest większa niż liczba wyrzuconych reszek, 4. za drugim razem otrzymano reszkę, 5. w dwóch pierwszych rzutach otrzymano orła, 6. wypadły

3

orły lub

3

reszki Zdarzenia, których prawdopodobieństwa wynoszą

\frac{1}{4}

3

orły lub

3

reszki

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1BrXqfvBadil

Ćwiczenie 6

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Ćwiczenie 7

W urnie znajdują się $43$ kule, w tym kule białe, czarne i czerwone, przy czym kul czarnych jest o $11$ więcej niż białych, a kul czerwonych $6$ razy więcej niż białych. Losujemy raz $1$ kulę. Oblicz prawdopodobieństwo wylosowania kuli czerwonej.

R1bw3B8KKlysO

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ustal najpierw liczbę kul czarnych i czerwonych. W tym celu ułóż odpowiednie równanie. Zauważ, że jeśli $x$ jest liczbą kul białych, to liczba kul czarnych jest równa $x + 11$ , zaś liczba kul czerwonych to $6 x$ .

Wprowadźmy następujące oznaczenia:
$x$ – liczba kul białych,
$x + 11$ – liczba kul czarnych,
$6 x$ – liczba kul czerwonych.

Ponieważ liczba wszystkich kul jest równa $43$ , zatem do wyznaczenia wartości $x$ rozwiązujemy równanie:
$x + x + 11 + 6 x = 43$
$8 x + 11 = 43$
$8 x = 32$
$x = 4$
Zatem liczba kul czerwonych wynosi:
$6 \cdot 4 = 24$
Wyznaczamy prawdopodobieństwo wylosowania kuli czerwonej:
$n = 24$
$N = 43$
$p = \frac{24}{43}$

Wobec tego prawdopodobieństwo wylosowania kuli czerwonej jest równe $\frac{24}{43}$ .

Ćwiczenie 8

Rzucamy $2$ razy symetryczną czworościenną kostką do gry (mającą na ściankach liczby od $1$ do $4$ ). Oblicz prawdopodobieństwo zdarzenia polegającego na otrzymaniu:

sumy liczb mniejszej od $4$ ,
w drugim rzucie o $2$ więcej niż w pierwszym rzucie.

R1bw3B8KKlysO

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zauważ, że liczba wszystkich zdarzeń elementarnych jest równa $4 \cdot 4 = 16$ .

Przedstawmy w tabeli wyniki doświadczenia polegającego na dwukrotnym rzucie czworościenną kostką do gry:

RspAxmUUnmLe3

Ilustracja przedstawia tabelę, w której są zapisane możliwe wyniki dwukrotnego rzutu czworościenną kostką do gry. Pierwsza cyfra oznacza pierwszy rzut, druga cyfra oznacza drugi rzut. Możliwe wyniki, to 1,1, 1,2, 1,3, 1,4

2,1, 2,2, 2,3, 2,4

3,1, 3,2, 3,3, 3,4

4,1, 4,2, 4,3, 4,4. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zauważmy, że liczba wszystkich możliwych wyników jest równa $16$ .

Jeżeli suma wyrzuconych liczb jest mniejsza od $4$ , to mamy następujące możliwości: $(1, 1)$ , $(1, 2)$ , $(2, 1)$ .
Zatem: $n = 3$ , $N = 16$ .
Wobec tego prawdopodobieństwo otrzymania sumy liczb mniejszej od $4$ wynosi:
$p = \frac{3}{16}$ .
Jeżeli w drugim rzucie otrzymujemy o $2$ więcej niż w pierwszym rzucie, to mamy następujące możliwości: $(1, 3)$ , $(2, 4)$ .
Zatem: $n = 2$ , $N = 16$ .
Wobec tego prawdopodobieństwo otrzymania w drugim rzucie o $2$ więcej niż w pierwszym rzucie wynosi:
$p = \frac{2}{16}$ .

Słownik

doświadczenie losowe

doświadczenie, które można powtarzać wiele razy w tych samych warunkach, ale jego kolejnych wyników nie potrafimy przewidzieć.

Bibliografia

Billingsley P., tłum. Kizeweter K., Roguski J., (1987), Prawdopodobieństwo i miara, Warszawa: Wydawnictwo Naukowe PWN.
Jakubowski J., Sztencel R., (1987) Wstęp do teorii prawdopodobieństwa, Warszawa: Wydawnictwo Script.
Kiljańska B., Konstantynowicz A., Konstantynowicz A., Pająk M., Ukleja G., (2017), Matematyka $8$ . Podręcznik, Gdynia: Wydawnictwo Pedagogiczne Operon
Jakubowski J., Sztencel R., (2015), Rachunek prawdopodobieństwa dla (prawie) każdego, Kraków: Wydawnictwo Script.