Odczytywanie i interpretowanie danych
Zebrane informacje dotyczące na przykład liczby osób zamieszkałych w danym mieście, ulubionych potraw Polaków, koloru włosów piątoklasistów to dane statystyczne.
Gromadzeniem, opracowaniem i prezentacją oraz analizą danych zajmuje się statystyka opisowastatystyka opisowa. Głównym celem analiz statystycznych jest określenie prawidłowości rządzących danym zjawiskiem. Metody statystyki opisowej stosowane są w wielu dziedzinach wiedzy.
Pozyskane dane najczęściej zapisywane są za pomocą liczb. Jednak dla odbiorcy dużo czytelniejsze są informacje przedstawione graficznie.
W tym materiale będziemy odczytywać i interpretować dane przedstawione w różny sposób, w szczególności graficznie.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Prezentacja multimedialnaPrezentacja multimedialna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Odczytasz i zinterpretujesz dane zawarte w tekście, przedstawione w tabeli, na wykresie, diagramie, itp.
Przedstawisz różnymi sposobami dane statystyczne.
Informacje odczytujemy codziennie. Są one zawarte w książkach, gazetach, zamieszczane w wiadomościach telewizyjnych, możemy pozyskać je z internetu. Surowe dane statystyczne zwykle niewiele nam mówią, szczególnie gdy jest ich bardzo dużo. Dlatego po uporządkowaniu mają formę tabeli, wykresu, szeregu statystycznegoszeregu statystycznego, schematu, ilustracji.
Zapytano uczniów klasy szóstej o liczbę ich rodzeństwa. Uzyskano następujące wyniki:
, , , , , , , , , , , , , , , , , , , .
Pozyskane dane uporządkujemy rosnąco, tworząc szereg prosty.
Teraz możemy dane zgrupować tak, aby określić liczebność poszczególnych odpowiedzi. Utworzymy szereg rozdzielczy punktowy.
Liczba rodzeństwa | Liczba uczniów |
|---|---|
Razem |
Analizując pozyskane dane możemy ustalić na przykład, że:
na zadanie pytanie odpowiedziało uczniów,
tylko jeden uczeń ma pięcioro rodzeństwa,
aż siedmioro uczniów ma tylko jednego brata lub siostrę.
Dwudziestu przechodniów zapytano o ich ulubiony kolor. Zebrane dane przedstawiono w tabeli.
Ulubiony kolor | Liczba wskazań |
|---|---|
biały | |
zielony | |
niebieski | |
czarny | |
czerwony |
Z tabeli można odczytać na przykład, że:
osób najbardziej lubi kolor biały,
koloru czarnego nikt nie lubi,
kolor niebieski jest ulubionym kolorem aż osób,
czerwony kolor lubi o osób mniej niż kolor biały,
tylko jedna osoba uznała, że najbardziej lubi kolor zielony.
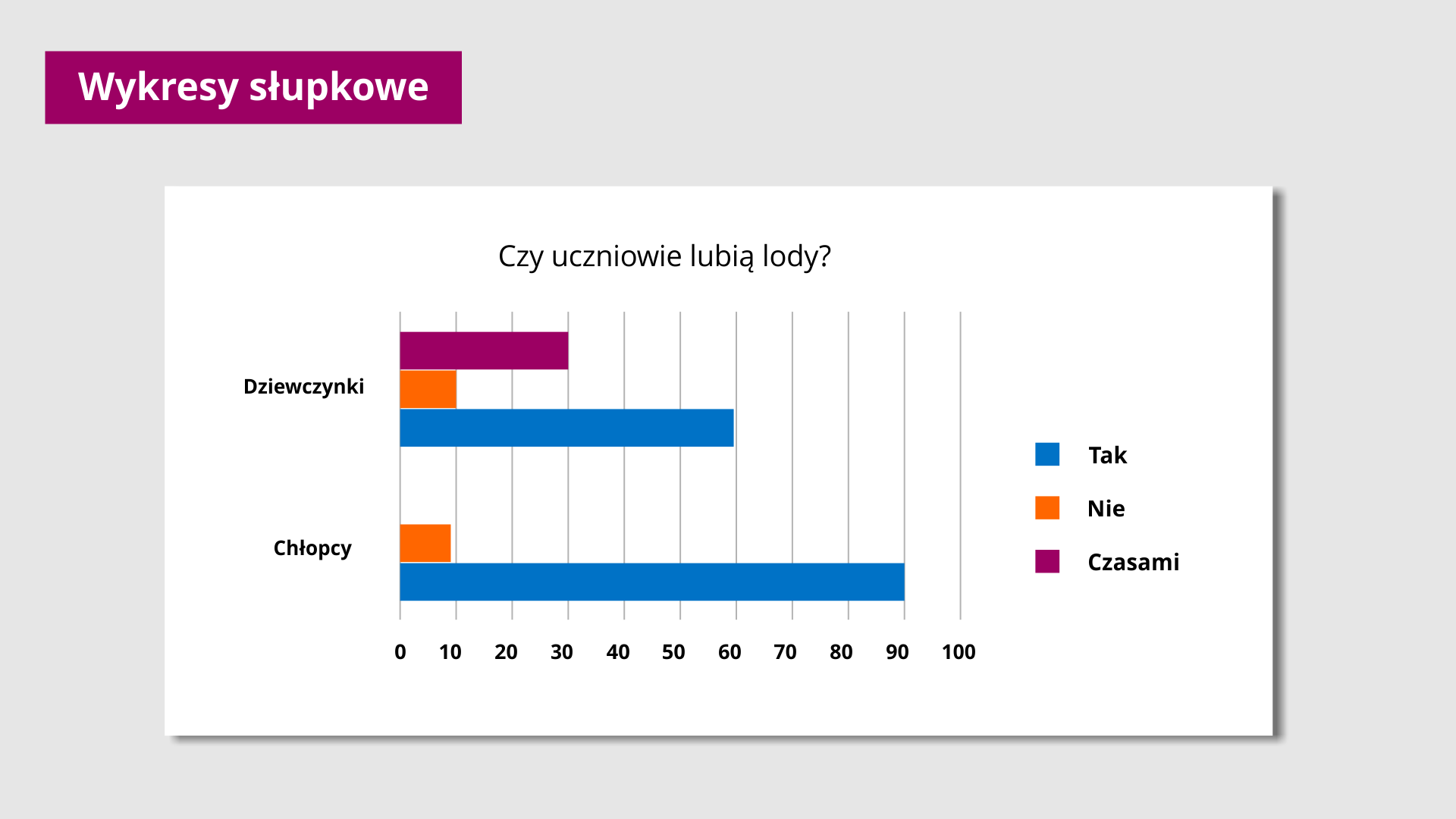
Do ilustrowania porównań elementów lub zmian danych w czasie wykorzystuje się często wykresy słupkowe. Na takim wykresie dane przedstawiane są w postaci słupków. Długość lub wysokość słupka odpowiada wartości, którą reprezentuje. Słupki mogą być pionowe (taki wykres nazywany jest też wykresem kolumnowym) lub poziome.
Na wykresach kolumnowych kategorie umieszczane są najczęściej na osi poziomej, a wartości na osi pionowej.
Jurek przez tydzień przygotowywał się do minimaratonu pływackiego. W tabeli zapisywał, ile kilometrów dziennie przepłynął.
Dzień tygodnia | Liczba kilometrów |
|---|---|
Poniedziałek | |
Wtorek | |
Środa | |
Czwartek | |
Piątek | |
Sobota | |
Niedziela | |
Razem |
Dane zapisane w tabeli zilustrujemy za pomocą wykresu słupkowego. Na takim wykresie łatwiej jest porównać prezentowane wielkości.
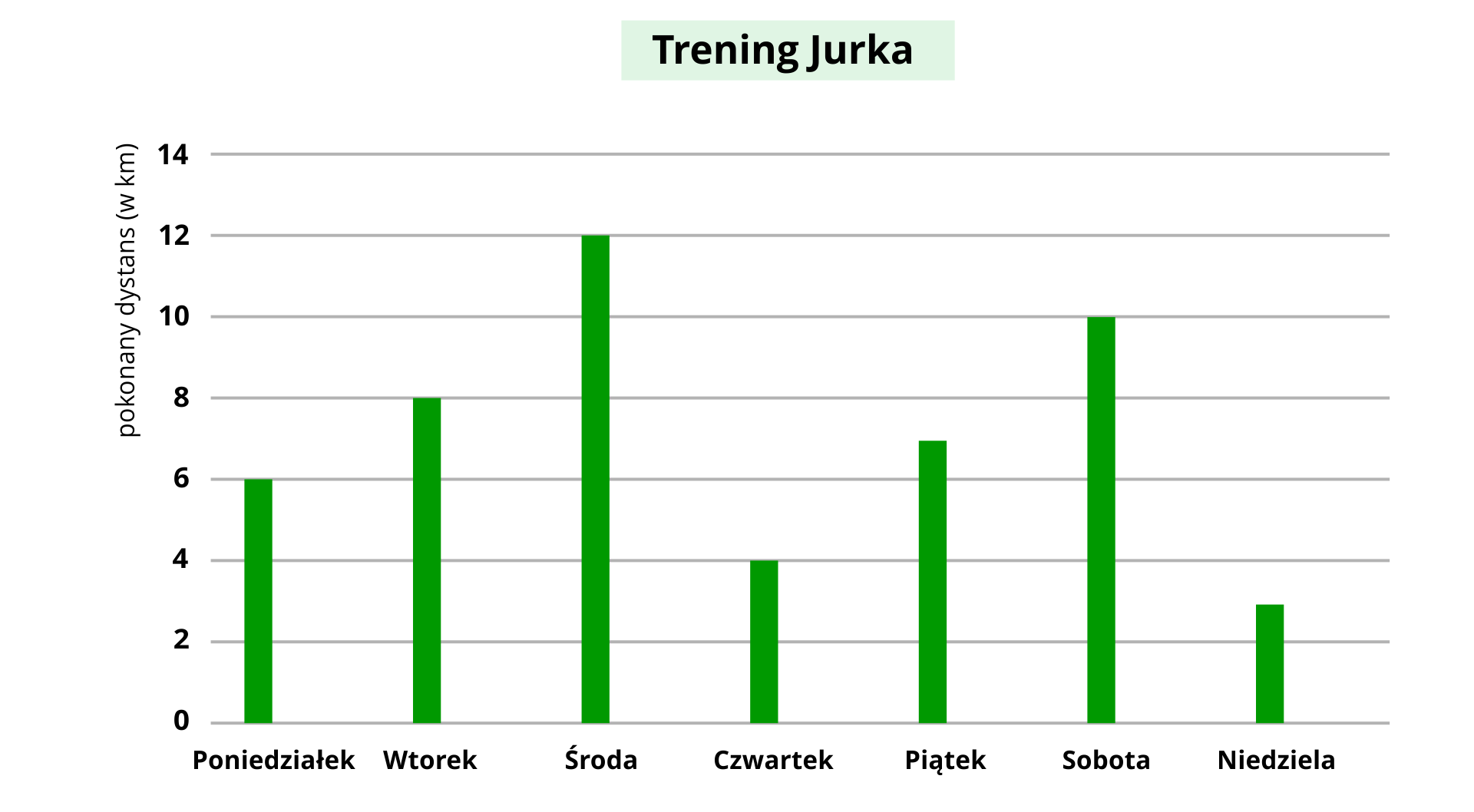
Patrząc na wykres, od razu możemy określić, że najwięcej kilometrów Jurek przepłynął w środę, a najmniej w niedzielę (o mniej niż w środę). Codziennie Jurek pokonywał inny dystans.
Pokażemy teraz zastosowanie wykresu słupkowego do porównania danych zebranych od różnych grup respondentów.
Wśród uczniów klasy i klasy zebrano dane na temat ocen, jakie uzyskali na okres z języka polskiego, matematyki, historii i wychowania fizycznego. Obliczono średnie tych ocen i wyniki przedstawiono na wykresie słupkowym.
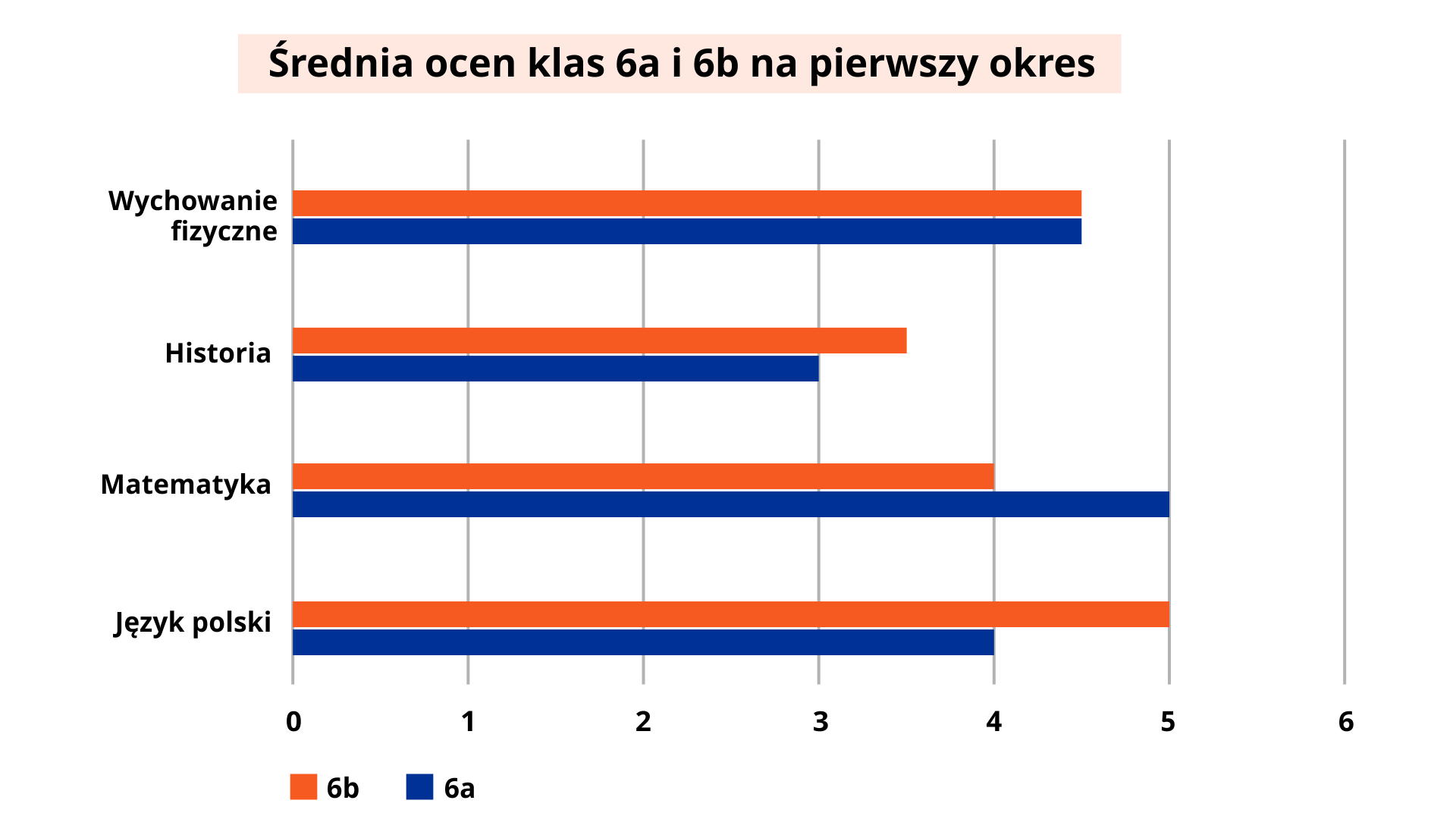
Na podstawie wykresu możemy stwierdzić na przykład, że:
średnia ocen z wychowania fizycznego w obu klasach była taka sama i wynosiła ,
klasa uzyskała lepszą średnią ocen od klasy tylko z matematyki,
najniższa średnia ocen w obu klasach była z historii.
Do prezentacji zmian w czasie pojedynczych zjawisk lub wielkości, można zastosować wykres liniowy.
W ciągu tygodnia mierzono temperaturę powietrza w miejscowościach Tutu i Tamtam. Zebrane dane przedstawiono na wykresie liniowym.
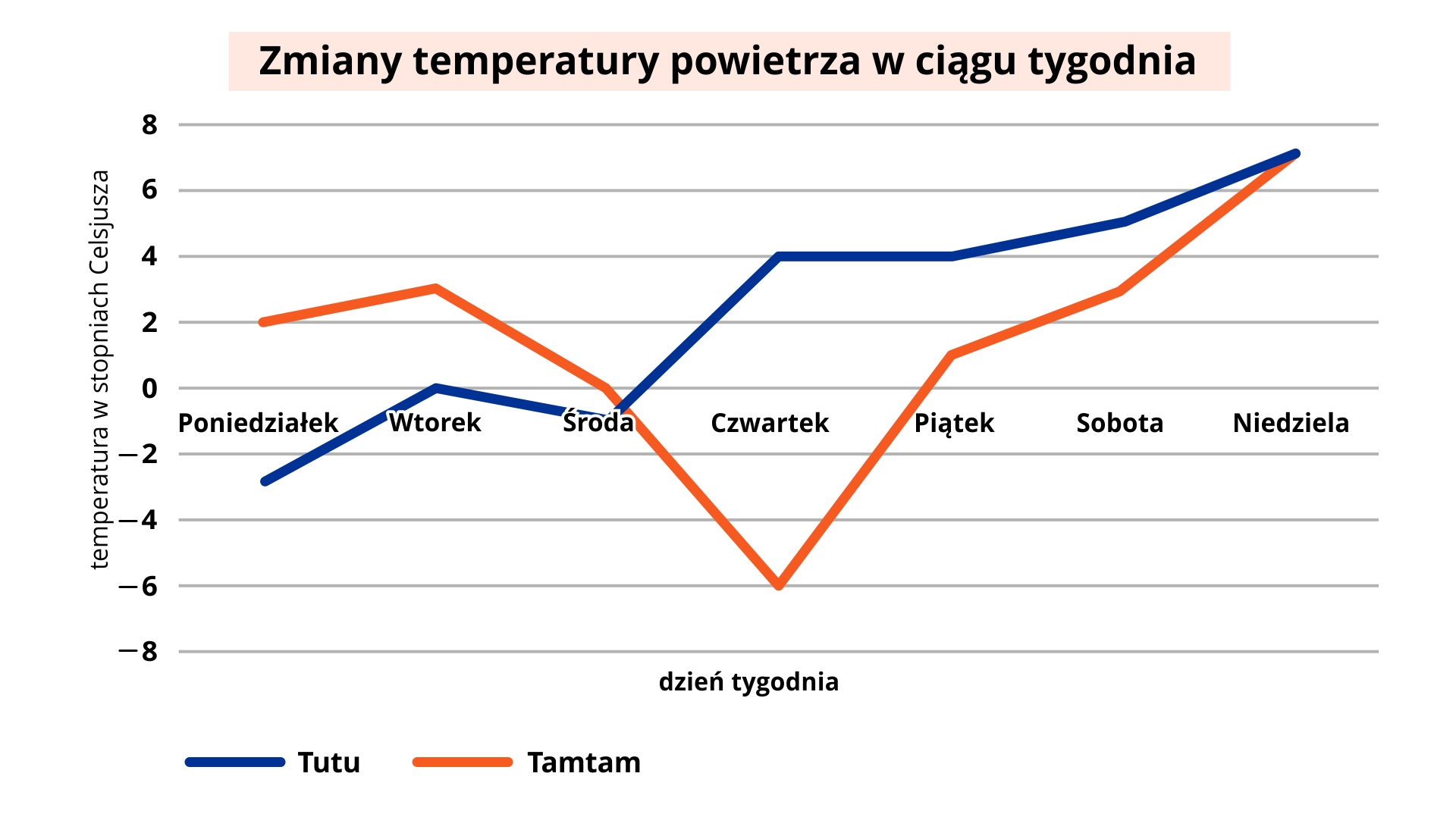
Z wykresu można odczytać, że:
w obu miejscowościach w ciągu tygodnia były duże wahania temperatury powietrza, dopiero pod koniec tygodnia temperatura stale rosła,
najniższa temperatura panowała w czwartek w miejscowości Tamtam i wynosiła ,
w niedzielę w obu miejscowościach panowała ta sama temperatura i wynosiła ,
w miejscowości Tamtam różnica między najwyższą a najniższą temperaturą wynosiła .
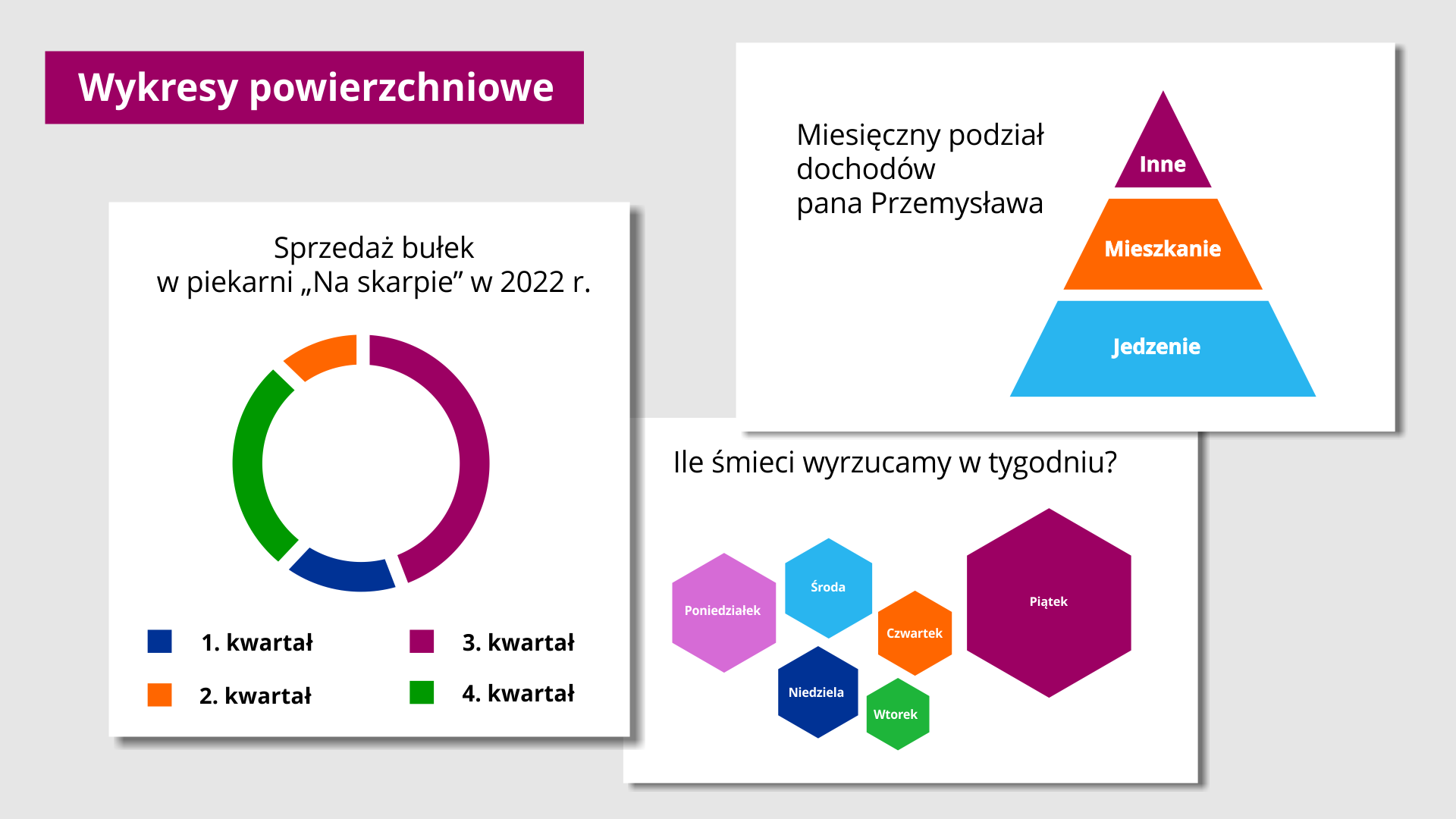
Wykresy powierzchniowe mają postać figur płaskich ( np. prostokątów, trójkątów równobocznych, kół). W graficznej prezentacji wykorzystywane są najczęściej pola tych figur dostosowane wielkością do zjawiska, które ilustrują.
Weronika przesłała Izie wykres obrazujący zawartość jej biblioteczki. Na wykresie jedna kratka oznacza dwie książki.
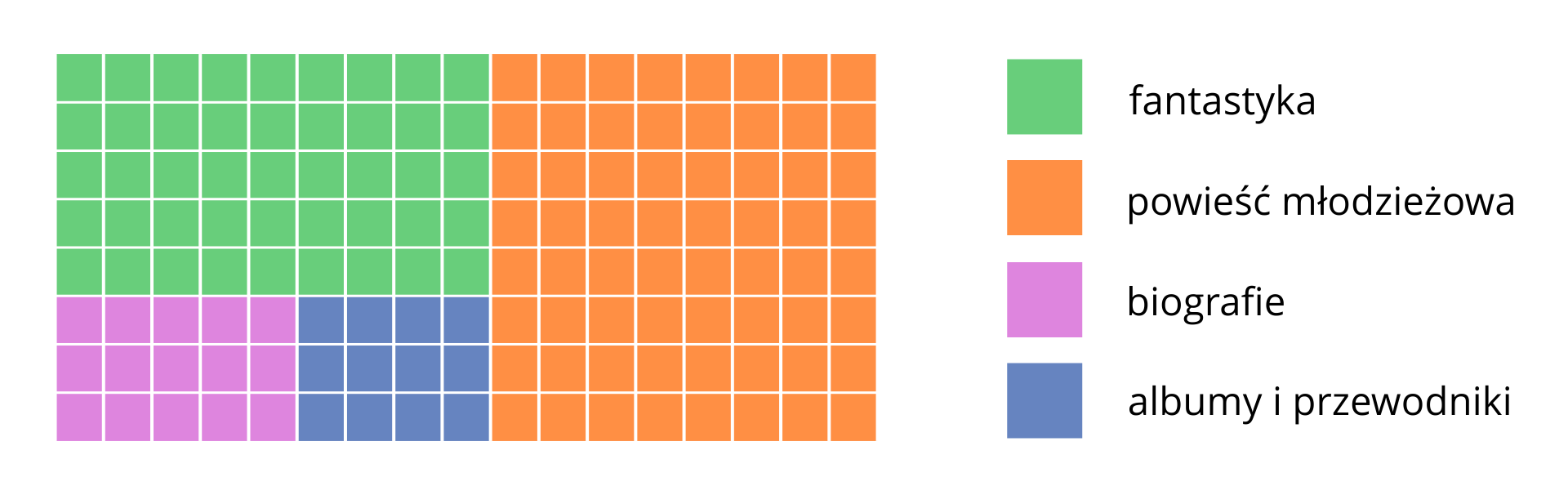
A oto, co Iza odpisała Weronice.
Weronika,
zauważyłam, że najwięcej książek w twojej biblioteczce to książki młodzieżowe – masz ich aż . Lubisz również czytać fantastykę – masz książek tego rodzaju. Dużo miejsca w twoich zbiorach zajmują też biografie – jest ich co prawda o mniej niż fantastyki, ale za to o więcej niż albumów i przewodników. Obliczyłam, że wszystkich książek masz . Aby wzbogacić Twoje zbiory przesyłam Ci jeszcze jedną powieść młodzieżową. Mam nadzieję, że Ci się spodoba.
Z serdecznymi pozdrowieniami,
Iza.
Notatki
Prezentacja multimedialna
Zapoznaj się z prezentacją, a następnie odpowiedz – jaki rodzaj wykresu warto wybrać, aby zilustrować zmiany ciśnienia atmosferycznego.
Pierwszy slajd:
Codziennie uzyskujemy nowe informacje. Możemy je zdobywać celowo, na przykład ze szkolnych podręczników. Idąc ulicą lub oglądając telewizję pozyskujemy przypadkowe dane zamieszczone na bilbordach, witrynach sklepów, w spotach reklamowych. Najlepiej zapamiętujemy te, które przedstawione są graficznie. Graficzna interpretacja danych jest również celowa wtedy, gdy zebranych informacji na określony temat jest bardzo dużo i dopiero odpowiednio pogrupowane pozwalają na poprawne ich zinterpretowanie. Umiejętność szybkiego odczytywania, analizowania, interpretowania i tworzenia materiałów wizualnych jest bardzo ważna w zdominowanej cyfrowo rzeczywistości. Coraz częściej poszukujemy informacji w sieci internetowej - ciekawy element graficznych łatwiej zachęci do przeczytania całego materiału. Szybkość odczytywania informacji przedstawionych graficznie jest najbardziej istotna w sytuacjach związanych z niebezpieczeństwem przykładem może być interpretowanie piktogramów zamieszczonych na znakach drogowych.
O to kilka przykładów prezentacji danych i informacji.
Przykład pierwszy:
Grafika przedstawiająca etapy wzrostu roślin znajdująca się w podręczniku szkolnym. Skład się ona z pięciu kopczyków ziemi. Na pierwszym kopczyku ziemi leży nasionko rośliny, z drugiego kopczyka wyrastają pędy młodej rośliny z jednym liściem. Z trzeciego kopczyka wyrasta większa roślina z dwoma liśćmi. Z czwartego kopczyka wyrastają trzy pędy rośliny zakończone kwiatostanem przed kwitnięciem. Z ostatniego kopczyka wyrasta dojrzała roślina zakończona kwiatostanem.
Przykład drugi:
Grafika przedstawia ofertę sklepu obuwniczego. Po prawej stronie grafiki znajduję się witryna, na której poustawiane są szpilki w różnych kolorach. Na środku znajduje się koło na którym widnieje napis minus pięćdziesiąt na wszystkie czółenka. Po lewej stronie znajduje się napis oferta ważna tylko do środy. Poprowadzono strzałkę od napisu do wcześniej opisanego koło. W prawym dolnym rogu grafiki znajduje się małe koło z napisem minus pięćdziesiąt.
Przykład trzeci:
Grafika przedstawia kilka znaków drogowych, które można spotkać w przestrzeni publicznej. Pierwszy z nich to znak w kształcie rombu z pofalowaną strzałką oraz tabliczką pod spodem w języku angielskim next four miles.
Drugi znak, to oznaczenie na asfalcie przedstawiające czteroosobową rodzinę z dwójką małych dzieci.
Trzeci znak jest w kształcie trójkąta i przedstawia graficznie wielbłąda. Poniżej pierwszego znaku znajduje się kolejny znak w kształcie trójkąta z narysowanym wykrzyknikiem.
Przykład czwarty:
Grafika przedstawia ekran telefonu, który wyświetla galerię zdjęć. Zdjęcia w kształcie kwadratów ułożone są w dwóch kolumnach obok siebie.
Zapraszamy cię do zapoznania się z kilkoma najprostszymi formami graficznej prezentacji danych.
Drugi slajd:
Rodzaj zastosowanej wizualizacji zależy od liczby zebranych danych, ich rodzaju. Powinien być tak dobrany, aby łatwo można było z niego odczytać potrzebne informacje. Najczęściej stosowanymi formami graficznej prezentacji danych są wykresy.
Na planszy znajduje się wiele grafik.
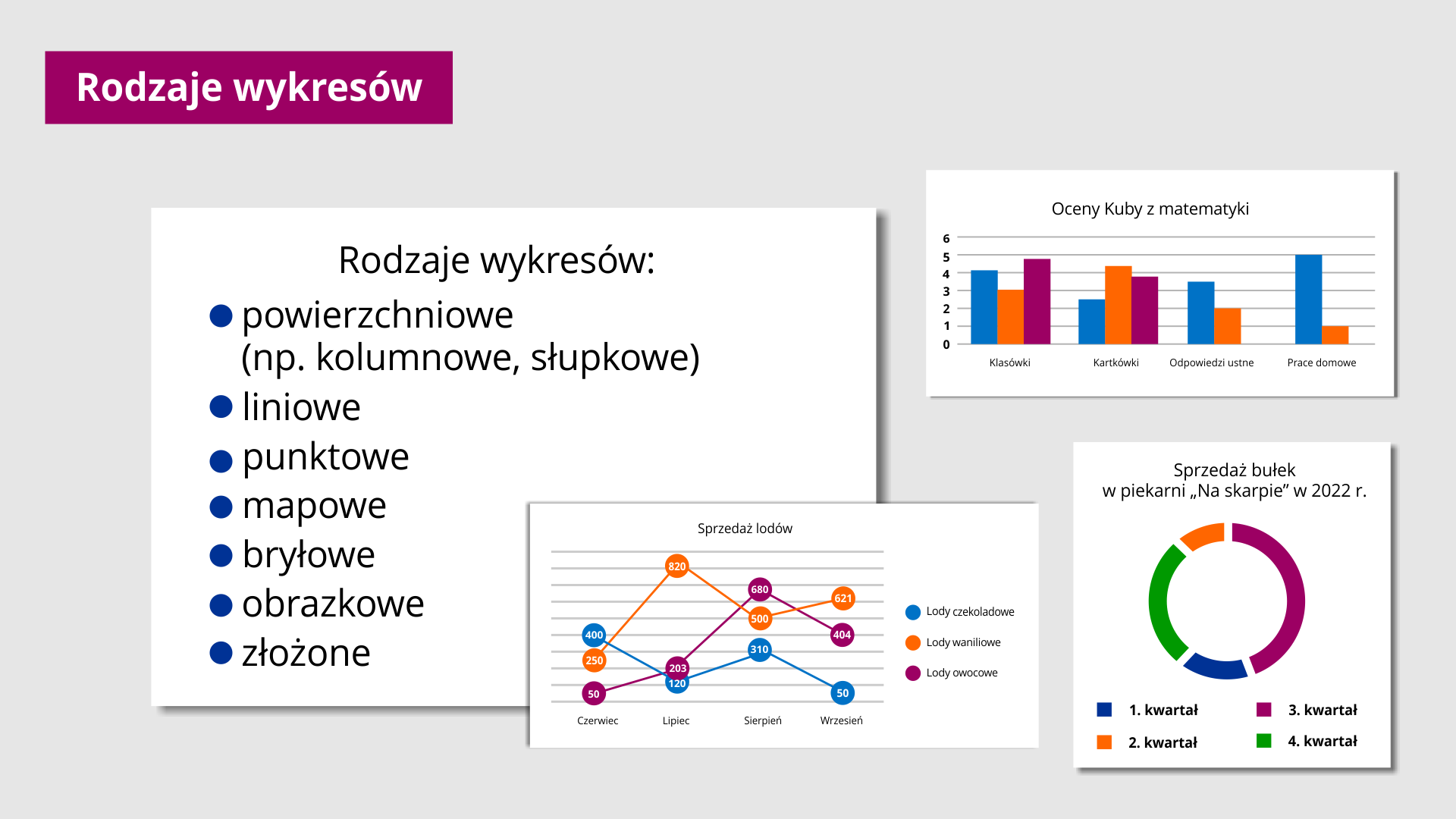
Grafika pierwsza wypisuje słownie rodzaje wykresów.
Rodzaje wykresów: powierzchniowe na przykład kolumnowe, słupkowe; liniowe; punktowe; mapowe; bryłowe; obrazkowe; złożone.
Druga grafika przedstawia wykres składający się z prostokątów opisujący oceny Kuby z matematyki. Na osi poziomej zapisano kolejno klasówki, kartkówki, odpowiedzi ustne oraz prace domowe. Na osi pionowej zapisano liczby od zera do sześciu rosnąco o jeden. Przy klasówkach znajdują się trzy słupki oznaczające trzy oceny kolejno jest to czwórka, trójką oraz piątka. Przy kartkówkach znajdują się trzy słupki oznaczające trzy oceny kolejno jest to dwójka, czwórka i czwórka. Przy odpowiedzi ustnej znajdują się dwa słupki oznaczające dwie oceny kolejno czwórkę i dwójkę. Przy pracy domowej mamy dwa słupki oznaczające dwie oceny kolejno jest to piąta i jedynka.
Trzecia grafika przedstawia wykres w postaci pierścienia opisujący sprzedaż bułek w piekarni na skarpie w dwa tysiące dwudziestym drugim roku. Kolejno kolorem granatowym oznaczono pierwszy kwartał, żółtym - drugi, trzeci różowym i czwarty zielonym. Z wykresu że największą sprzedaż bułek piekarnia odnotowała w czwartym kwartale, następnie w trzecim, potem pierwszym i najmniej w drugim.
Czwarta grafika przedstawia wykres opisujący sprzedaż smaków lodów takich jak: czekoladowy, owocowe i waniliowy podczas czterech miesięcy, czyli od czerwca do września włącznie za pomocą linii. Na osi poziomej zapisano miesiące. Kolorem niebieskim oznaczono lody czekoladowe, kolorem żółtym lody waniliowe, a kolorem różowym lody owocowe. Z wykresu można odczytać, że w czerwcu najwięcej sprzedano lodów czekoladowych, w lipcu sprzedano najwięcej lodów waniliowych, w sierpniu najwięcej lodów owocowych i we wrześniu najwięcej lodów waniliowych.
Trzeci slajd:
Wykresy powierzchniowe mają postać figur płaskich – na przykład prostokątów, trójkątów równobocznych, kół.
W graficznej prezentacji wykorzystywane są najczęściej pola tych figur dostosowane wielkością do zjawiska, które ilustrują.
Na planszy pojawiają się trzy grafiki.
Pierwsza grafika przedstawia wykres powierchniowy w postaci pierścienia opisujący sprzedaż bułek w piekarni na skarpie w dwa tysiące dwudziestym drugim roku. Kolejno kolorem granatowym oznaczono pierwszy kwartał, żółtym - drugi, trzeci różowym i czwarty zielonym. Z wykresu że największą sprzedaż bułek piekarnia odnotowała w czwartym kwartale, następnie w trzecim, potem pierwszym i najmniej w drugim.
Druga grafika przedstawia wykres powierzchniowy w kształcie trójkąta podzielonego na trzy części poziomymi liniami. Opisuje on miesięczny podział dochodów pana Przemysława. Kolejno od dołu zapisane są następujące wydatki: jedzenie, mieszkanie, inne.
Trzecia grafika przedstawia wykres powierzchniowy składający się z siedmiu sześciokątów różnej wielkości. Opisuje on ile śmieci wyrzucamy w tygodniu. Na każdym sześciokącie zapisano inną nazwę dnia tygodnia. Największy sześciokąt jest z napisem piątek, a najmniejszy z napisem wtorek.
Czwarty slajd:
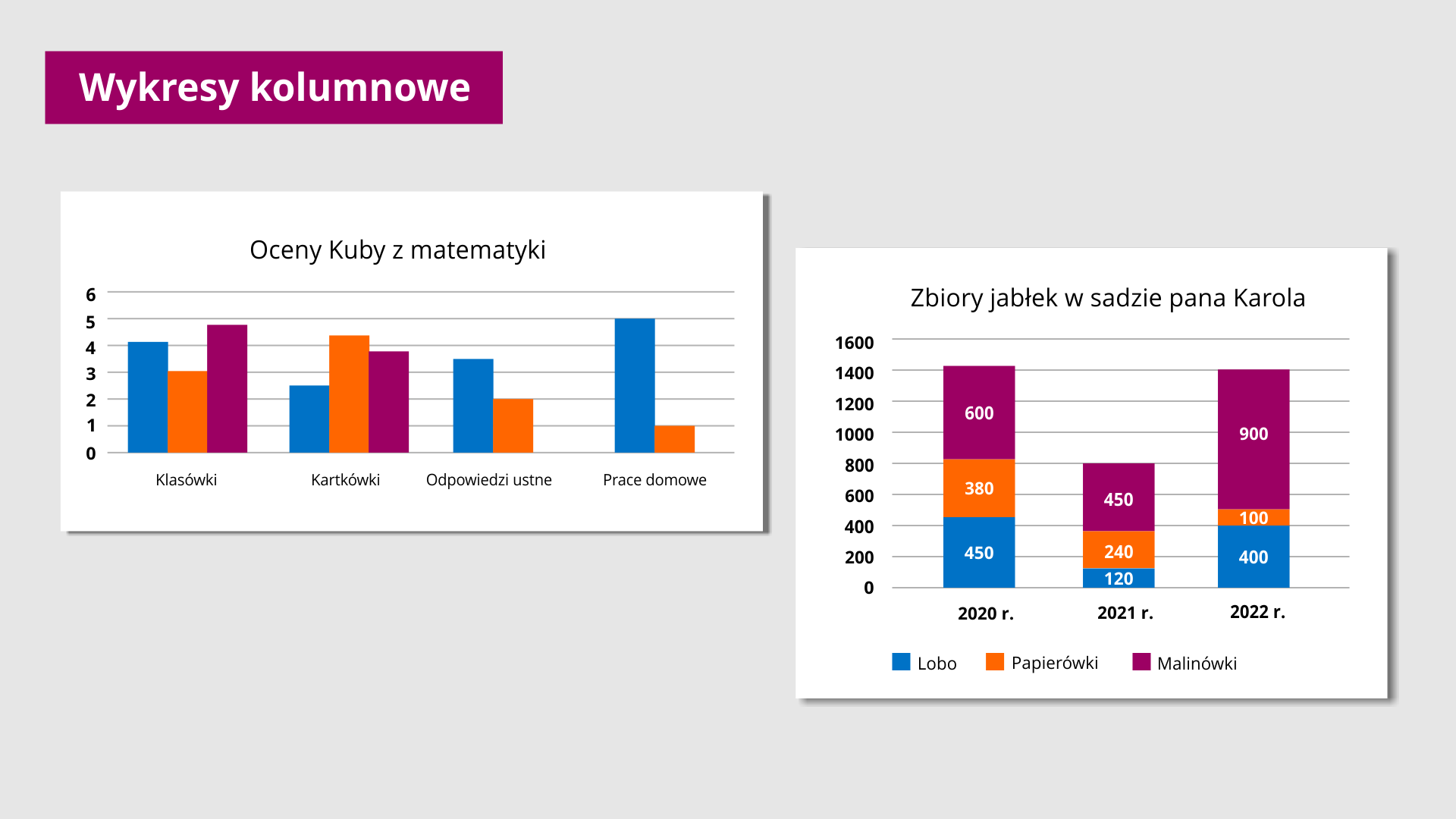
Wykresy kolumnowe składają się z prostokątów (kolumn) o jednakowej szerokości. Miarą wartości jest ich wysokość. Za ich pomocą można prezentować jedną lub kilka serii danych.
Na planszy znajdują się dwie grafiki.
Pierwsza grafika przedstawia wykres kolumnowy opisujący oceny Kuby z matematyki. Na osi poziomej zapisano kolejno klasówki, kartkówki, odpowiedzi ustne oraz prace domowe. Na osi pionowej zapisano liczby od zera do sześciu rosnąco o jeden. Przy klasówkach znajdują się trzy słupki oznaczające trzy oceny kolejno jest to czwórka, trójką oraz piątka. Przy kartkówkach znajdują się trzy słupki oznaczające trzy oceny kolejno jest to dwójka, czwórka i czwórka. Przy odpowiedzi ustnej znajdują się dwa słupki oznaczające dwie oceny kolejno czwórkę i dwójkę. Przy pracy domowej mamy dwa słupki oznaczające dwie oceny kolejno jest to piąta i jedynka.
Druga grafika przedstawia wykres kolumnowy opisujący zbiory jabłek w sadzie Pana Karola. Na osi poziomej zapisano kolejno od lewej strony lata dwa tysiące dwudziesty, dwa tysiące dwudziesty pierwszy oraz dwa tysiące dwudziesty drugi. Na osi pionowej od dołu do góry zapisano liczby od zera do tysiąca sześćset rosnące do dwieście. Każdy słupek składa się z trzech kolorów oznaczający ilość zebranych jabłek w podziałem na gatunki. Kolorem niebieskim oznaczono lobo, kolorem żółtym papierówki, a kolorem różowym malinówki. Wówczas w dwa tysiące dwudziestym roku zebrano czterysta pięćdziesiąt lobo, trzysta osiemdziesiąt papierówek i sześćset malinówek, w dwa tysiące dwudziestym pierwszym roku zebrano sto dwadzieścia lobo, dwieście czterdzieści papierówek i czterysta pięćdziesiąt malinówek. W ostatnim roku zebrano czterysta lobo, sto papierówek i dziewięćset malinówek.
Piąty slajd:
Wykresy słupkowe, podobnie jak wykresy kolumnowe, składają się z prostokątów o jednakowej szerokości. Miarą wartości jest ich długość.
Na planszy znajduję się jeden wykres słupkowy przedstawiający odpowiedź na pytanie ile lodów zjadły dzieci podczas wakacji. Na osi pionowej zapisano kolejno od lewej liczby od zera do stu rosnące co dziesięć. Na osi poziomej zapisano dziewczynki i chłopcy. Z wykresu wynika, że dziewczynki zjadły trzydzieści lodów czekoladowych, dziesięć owocowych i sześćdziesiąt owocowych. Chłopcy zjedli dziesięć lodów waniliowych i dziewięćdziesiąt owocowych.
Szósty slajd:
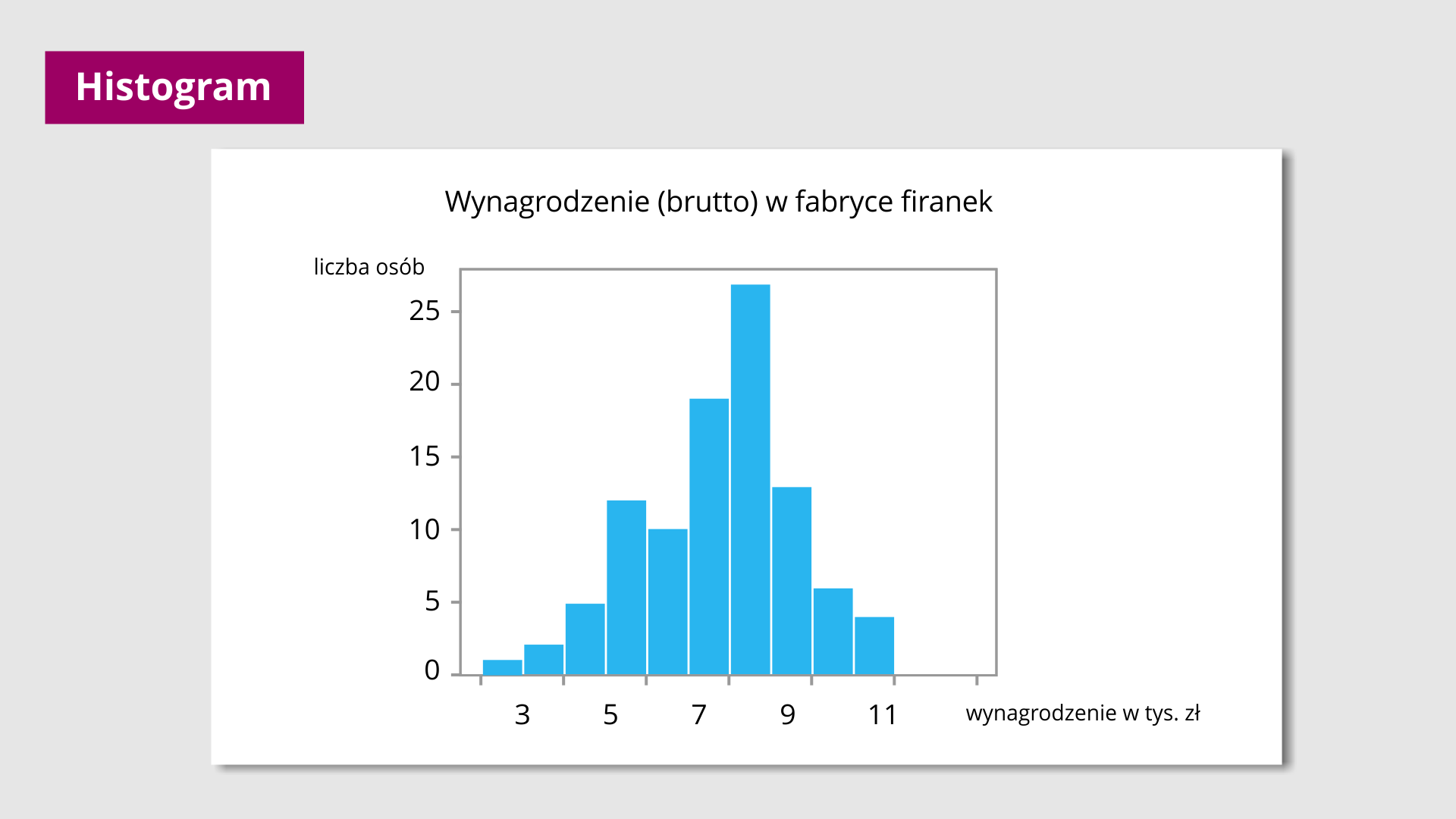
Histogram to wykres kolumnowy, w którym kolumny przylegają do siebie i których wysokość wskazuje liczebność elementów z danego przedziału, zaznaczonego na poziomej osi.
Na planszy przedstawiono jeden histogram opisujący wynagrodzenie dla pracowników w fabryce firanek. Na osi poziomej zapisano kolejno liczby od trzech do jedenastu rosnące co dwa. Liczby te oznaczają tysiące złotych. Na osi pionowej zapisano liczby od zera do dwudziestu pięciu rosnące do pięć oznaczające liczby osób. Za pomocą prostokątów różnych wysokości, ale tej samej szerokości zapisano kolejno zarobki osób w tej fabryce. Wówczas trzy tysiące złotych zarabiają dwie osoby, cztery tysiące złotych zarabiają trzy osoby, pięć tysięcy złotych zarabia pięć osób, sześć tysięcy złotych zarabia dwanaście osób, siedem tysięcy złotych zarabia dziesięć osób, osiem tysięcy złotych zarabia osiemnaście osób, dziewięć tysięcy złotych zarabia dwadzieścia pięć osób, dziesięć tysięcy złotych zarabia trzynaście osób, jedenaście tysięcy złotych zarabia sześć osób i dwanaście tysięcy złotych zarabia pięć osób.
Siódmy slajd:
Wykresy punktowe przedstawiają zależności zachodzące między wielkościami w postaci punktów.
Na planszy przedstawiono jeden wykres punktowy opisujący wybory przewodniczącego klasy. Na osi poziomej zapisano kolejno numery kandydatów od jednego do siedmiu. Na osi pionowej zapisano liczbę zebranych głosów od zera do dwunastu rosnącego w górę co dwa.
Punktami zaznaczono kolejne wyniki głosowania. Kandydat z numerem jeden nie zebrał żadnego głosy, kandydat z numerem dwa zebrał siedem głosów, kandydat z numerem trzy nie zebrał żadnego głosy, kandydat numer cztery zebrał cztery głosy, kandydat z numerem pięć nie zebrał żadnego głosu, kandydat z numerem sześć zebrał dziesięć głosów i kandydat z numerem siedem nie zebrał żadnego głosu.
Ósmy slajd:
Na wykresie kołowym powierzchnię koła przyjmuje się najczęściej za 100 procent. Trzystu sześćdziesięciu stopniom odpowiada więc sto procent. Zatem jednemu procentowi odpowiada trzy i sześć dziesiątych stopnia.
Na wykresie kołowym dany wycinek koła jest proporcjonalny do ilości, jaką przedstawia.
Na planszy przedstawiony jest jeden wykres kołowy opisujący ilość wypożyczonych książek w klasach pięć - osiem. Największą część wykresu kołowego zajmuje klasa piąta, następnie siódma, ósma, czwarta i na końcu szósta klasa.
Dziewiąty slajd:
Wykresy liniowe służą do prezentacji zmian w czasie pojedynczych zjawisk.
Na planszy przedstawiono jeden wykres liniowy. Wykres opisuje sprzedaż smaków lodów takich jak: czekoladowy, owocowe i waniliowy podczas czterech miesięcy, czyli od czerwca do września włącznie za pomocą linii. Na osi poziomej zapisano miesiące. Kolorem niebieskim oznaczono lody czekoladowe, kolorem żółtym lody waniliowe, a kolorem różowym lody owocowe. Z wykresu można odczytać, że w czerwcu sprzedano czterysta lodów czekoladowych, dwieście pięćdziesiąt waniliowych i pięćdziesiąt owocowych, w lipcu sprzedano osiemset dwadzieścia lodów waniliowych, dwieście trzy lody czekoladowe i sto dwadzieścia lodów czekoladowych, w sierpniu sprzedano sześćset osiemdziesiąt lodów owocowych, pięćset lodów waniliowych i trzysta dziesięć lodów czekoladowych i we wrześniu sprzedano sześćset dwadzieścia jeden lodów waniliowych, czterysta cztery lody waniliowe i trzysta dziesięć lodów czekoladowych.
Dziesiąty slajd:
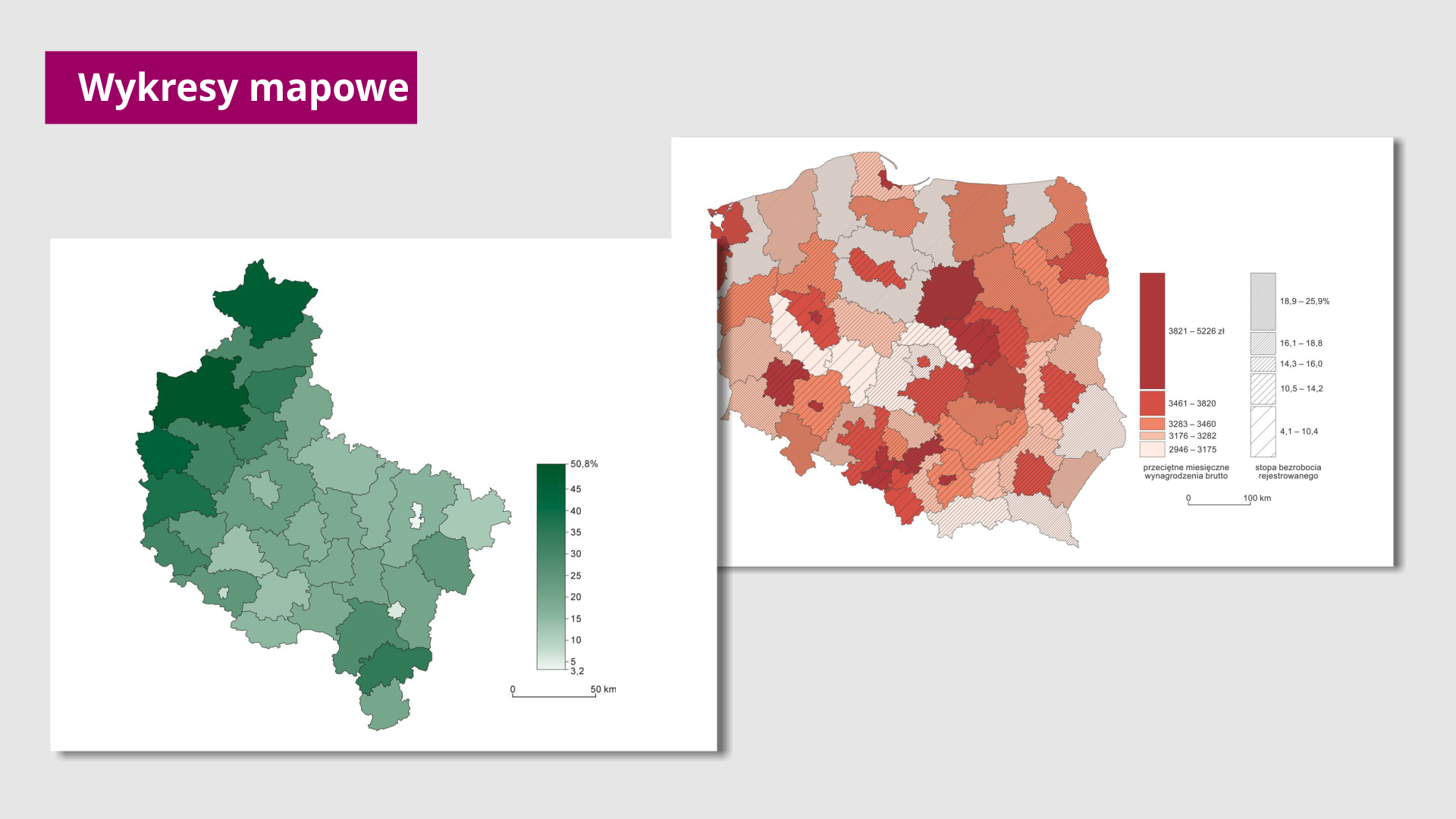
Na wykresach mapowych, zwanych też kartogramami, za pomocą barwnej skali prezentowane są różnice w natężeniu badanego zjawiska. Czym ciemniejszy kolor – tym większe natężenie zjawiska.
Na planszy przedstawione są dwa wykresy mapowe. Pierwszy z nich przedstawia zarys pewnego województwa z zaznaczonymi powiatami. Każdy z nim zaznaczonym jest innym odcieniem koloru zielonego, który oznacza pewną wartość w procentach od zera do pięćdziesięciu.
Drugi wykres mapowy przedstawia mapę Polski podzieloną na regiony. Pierwsza legenda składa się z różnych odcieni czerwonego oznaczające przeciętne wynagrodzenie brutto, a druga legenda składa się z różnych odcieni szarości oznaczające stopę bezrobocia.
Jedenasty slajd:
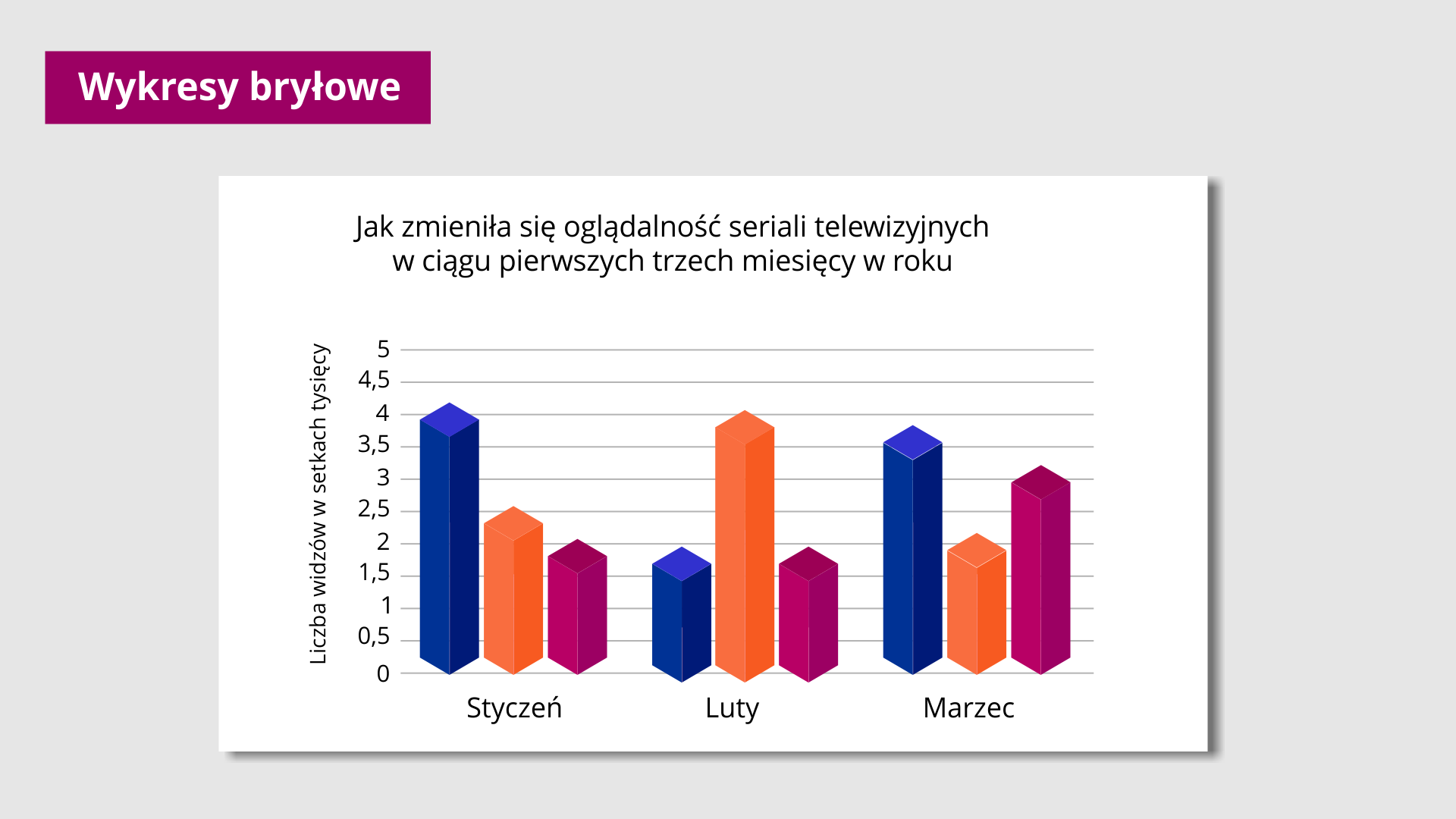
Na wykresach bryłowych wielkość zjawiska ilustrowana jest za pomocą objętości brył.
Na planszy przedstawiony jest jeden wykres bryłowy przedstawiający odpowiedź na pytanie jak zmieniła się oglądalność seriali telewizyjnych w ciągu pierwszych trzech miesięcy roku. Na osi pionowej zapisano kolejno trzy miesiące styczeń luty oraz marzec. Na osi pionowej zapisano liczby od zera do pięciu co pół oznaczające liczbę widzów w tysiącach. Analizowano trzy różne seriale oznaczone innymi kolorami brył. W styczniu serial numer jeden oglądało 4 tysiące widzów, serial numer dwa oglądało 2 tysiące pięćset widzów a serial numer trzy dwa tysiące widzów. W lutym serial numer jeden oglądało dwa tysiące widzów, serial numer dwa cztery tysiące widzów i serial numer trzy dwa tysiące widzów. W marcu serial numer jeden oglądało cztery tysiące widzów, serial numer dwa dwa tysiące widzów a serial numer trzy trzy tysiące widzów.
Dwunasty slajd:
Na wykresach obrazkowych przedstawiane są dane za pomocą znaków, symboli lub obrazków, odpowiadających swoim wyglądem opisywane zjawiska. Podstawowym celem tego typu wykresów jest przyciągnięcie uwagi odbiorcy.
Na planszy przedstawione są dwa wykresy obrazkowe. Pierwszy wykres odpowiada na pytanie Ile cukru dziennie można zjeść. Na rysunku narysowany jest jogurt owocowy, napój owocowy w szklanej butelce, tabliczka czekolady. Między produktami widnieje napis lub. W informacji po boku zapisano jogurt owocowy czterysta gram lub półtora litra napoju owocowego lub jedna tabliczka czekolady.
Drugi wykres obrazkowy przedstawia dwie sylwetki męską i żeńską. Każda z nich zakreślona jest kolorem niebiskim w siedemdziesięciu procentach. Oznacza to zawartość wody w organizmie mężczyzny i kobiety.
Trzynasty slajd:
Wykresy złożone łączą w sobie różne formy graficzne. Na przykład wykres słupkowy i liniowy. Za ich pomocą można przedstawiać jednocześnie kilka zjawisk powiązanych ze sobą logicznie. Na przykład temperaturę powietrza i ilość opadów atmosferycznych lub liczbę godzin nauki i otrzymaną ocenę szkolną.
Na planszy przedstawiony jest jeden wykres złożony opisujący zależność miedzy oceną z matematyki a liczbą godzin nauki. Składa się on z kolumn oraz wykresu liniowego. Kolumny opisują oceny, a wykres liniowy ilość godzin nauki. Z wykresu dowiadujemy się, że im mniej się uczymy, tym mniejszą ocenę uzyskujemy.
Koniec prezentacji.
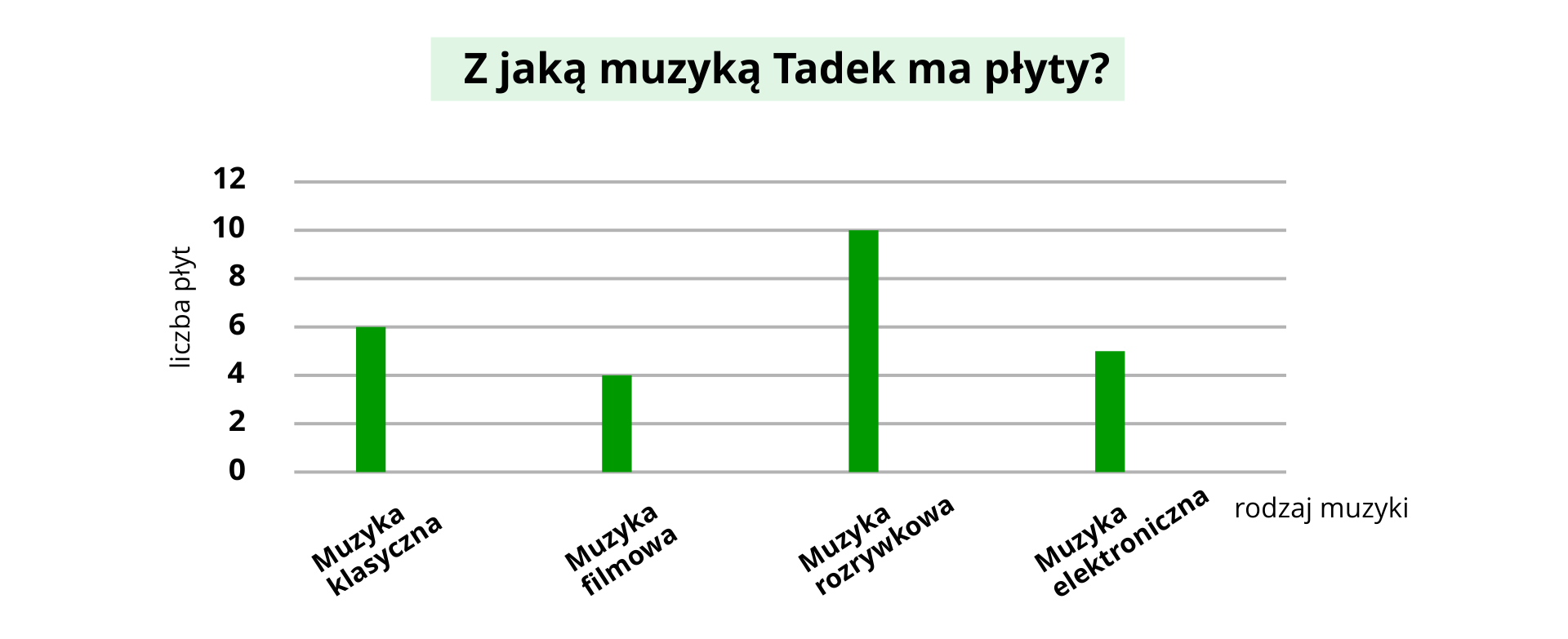
Tadek ma kolekcję płyt winylowych. Ma płyt z muzyką klasyczną, z muzyką filmową, z muzyką elektroniczną, z muzyką rozrywkową. Sporządź wykres kolumnowy opisujący dane przedstawione w zadaniu.
Tadek ma kolekcję płyt winylowych. Ma płyt z muzyką klasyczną, z muzyką filmową, z muzyką elektroniczną, z muzyką rozrywkową. Opisz słownie wykres kolumnowy opisujący dane przedstawione w zadaniu.
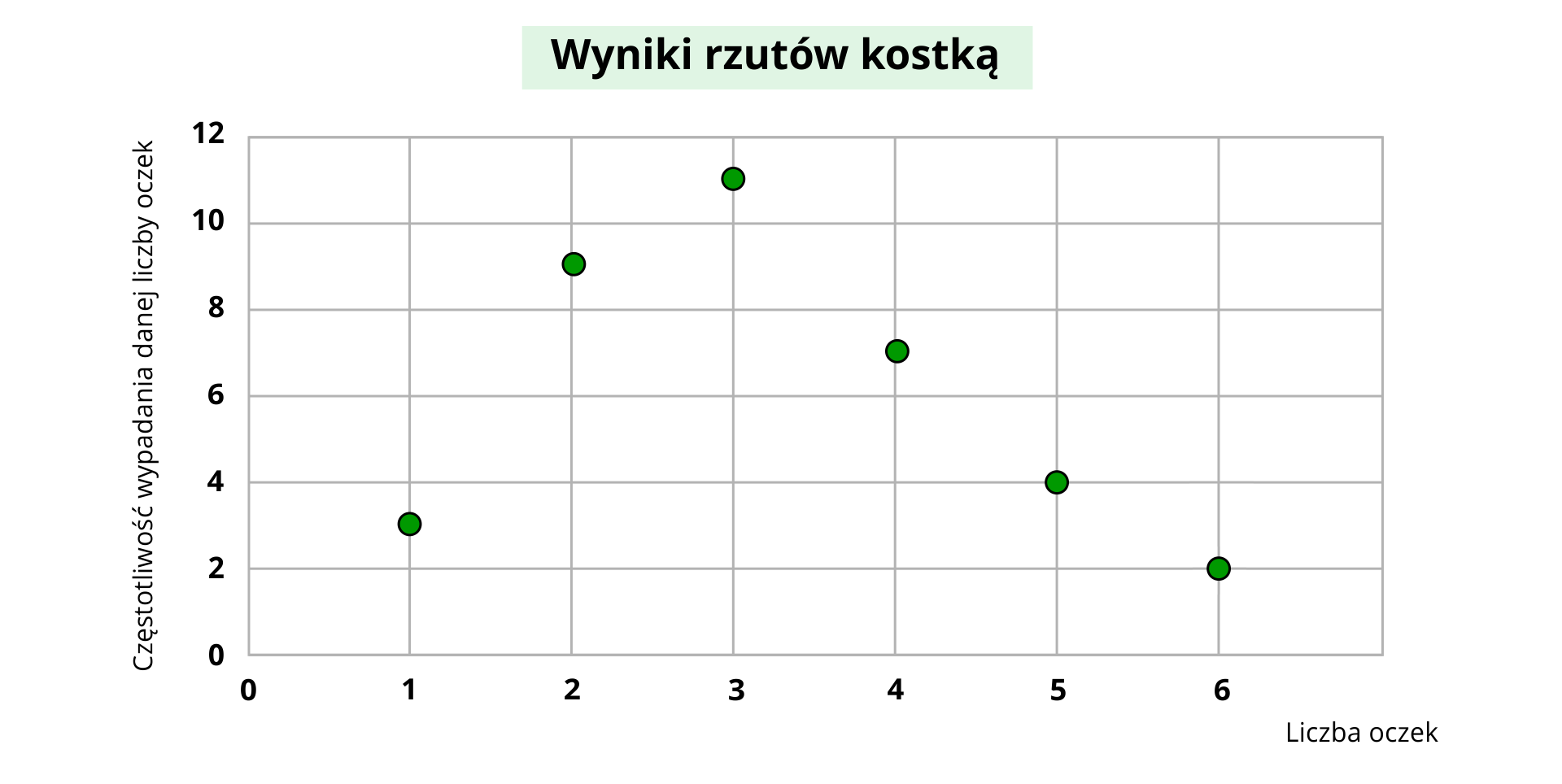
Sylwia rzucała kostką do gry. Wyniki zapisywała do tabeli.
Liczba oczek | Ile razy wypadła dana liczba oczek (częstość) |
|---|---|
Na podstawie tabeli sporządź odpowiedni wykres punktowy.
Na podstawie tabeli sporządź opis odpowiedniego wykresu punktowego.
Na diagramie przedstawiono wyniki ankiety, która została przeprowadzona wśród uczniów klasy pewnej szkoły. Dotyczyła ona odpowiedzi na pytanie „Ile godzin dziennie przeznaczasz na odrabianie prac domowych?”
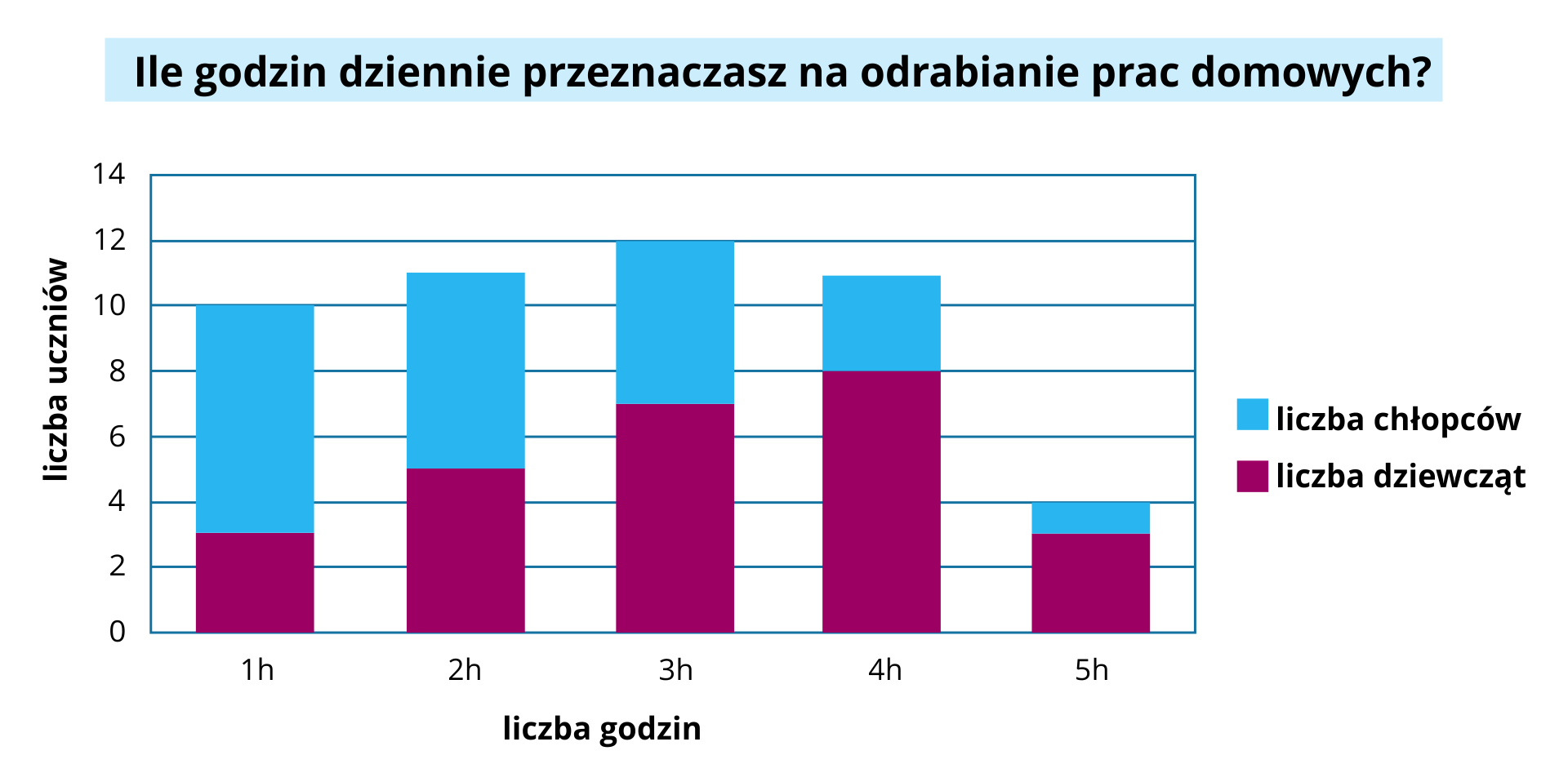
Na podstawie wykresu odpowiedz na pytanie. Ilu chłopców wzięło udział w ankiecie?
Gra edukacyjna
Statek kosmiczny, którym leciał Paweł do ciotki mieszkającej na Marsie zepsuł się i musiał lądować na Księżycu. Rozwiąż wszystkie zadania zapisane w Galaktycznej grze, a wystartuje rakieta, która zabierze Pawła z powrotem na Ziemię.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PcQWqmBEt
Na podstawie przedstawionych danych w tabeli połącz w pary pytanie i odpowiedź.
Nazwa planety | Liczba księżyców |
|---|---|
Merkury | |
Wenus | |
Mars | |
Ziemia | |
Uran | |
Jowisz | |
Saturn | |
Neptun |
Przeczytaj ofertę biura podróży Galaktyczne wyprawy i na podstawie zawartych w nim informacji – odpowiedz na pytania.

Biuro podróży Galaktyczne wyprawy
Zapraszamy Państwa do zwiedzania najbliższych nam planet. Pierwsza z naszych propozycji dotyczy Saturna. Co prawda jego masa jest aż razy większa od masy Ziemi, więc trudno będzie poruszać się po nim piechotą, ale za to stamtąd nasza trasa prowadzi na Marsa. Masa Marsa to masy Ziemi, więc będzie można po jego powierzchni swobodnie skakać.
Jeśli jednak zdecydujecie się najpierw polecieć na Jowisza (masa Jowisza jest razy większa od masy Ziemi), to czekają was niezwykłe widoki gwiazd niedostrzegalnych z Ziemi. Z kolei na podobnych nieco do siebie pod względem wielkości planetach Neptunie i Uranie (masa pierwszego jest razy większa od masy Ziemi, a drugiego tylko ) uruchomiono niedawno ogromne skocznie narciarskie.
Każdy więc znajdzie coś dla siebie. Ceny promocyjne!!!
Pytania:
Która z planet jest największa?
Która z planet jest najmniejsza?
Ile razy masa Ziemi jest mniejsza od masy Neptuna?
Która planeta jest większa – Wenus czy Mars?
Z której planety widać gwiazdy, których nie widać z Ziemi?
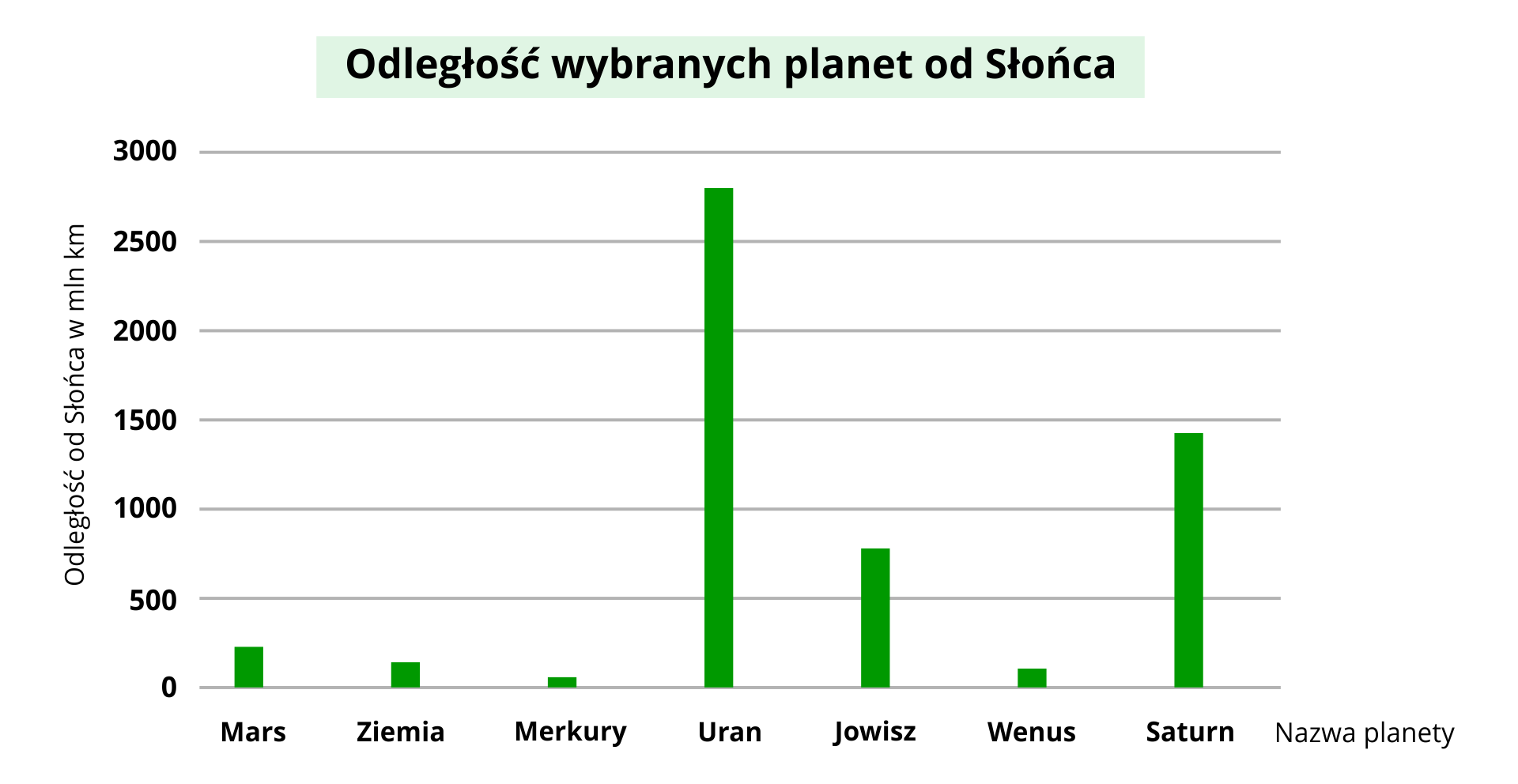
Korzystając z wykresu wypisz planety w kolejności od znajdującej się najbliżej Słońca do znajdującej się najdalej od Słońca.
Zestaw ćwiczeń interaktywnych
Zaznacz ten wykres.
Zaznacz prawidłową odpowiedź.
W klasie piątej odbyły się wybory najsympatyczniejszej dziewczynki. Wyniki głosowania przedstawiono na wykresie.
Która z dziewcząt zwyciężyła?
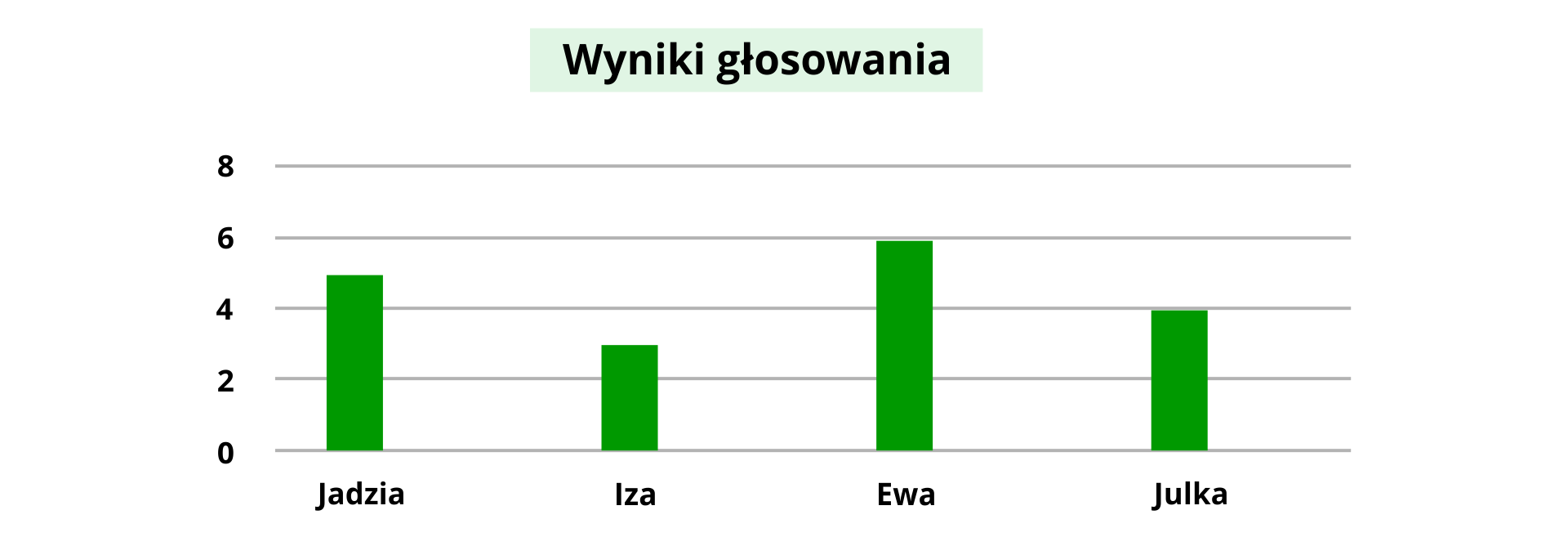
W klasie piątej odbyły się wybory najsympatyczniejszej dziewczynki. Po podliczeniu głosów wiadomo, że Iza zebrała trzy głosy, Ewa dwa razy więcej, Julka o dwa mniej od Ewy, a Jadzie o dwa głosy więcej od Izy. Która z dziewcząt zwyciężyła?
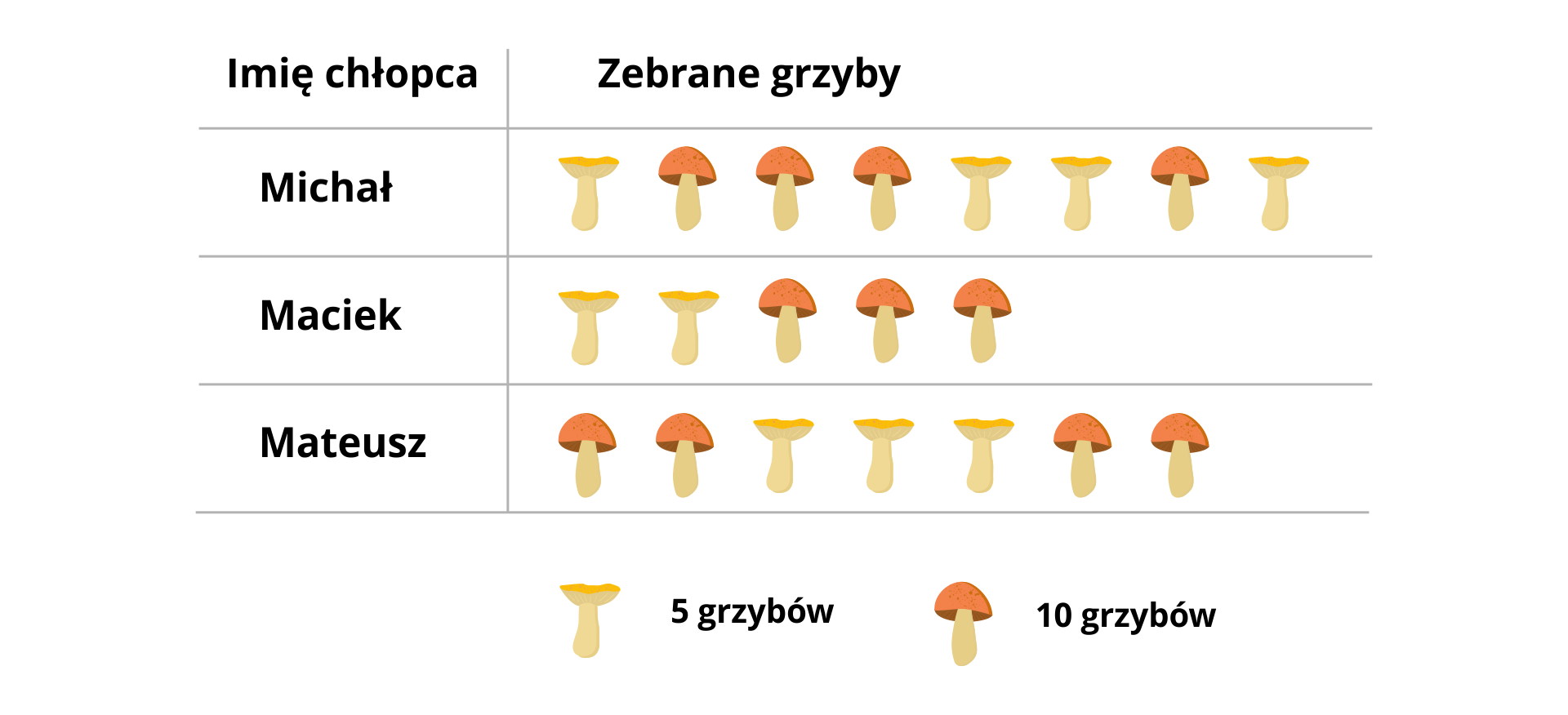
Na piktogramie przedstawiono, ile grzybów zebrali chłopcy w dniu września.
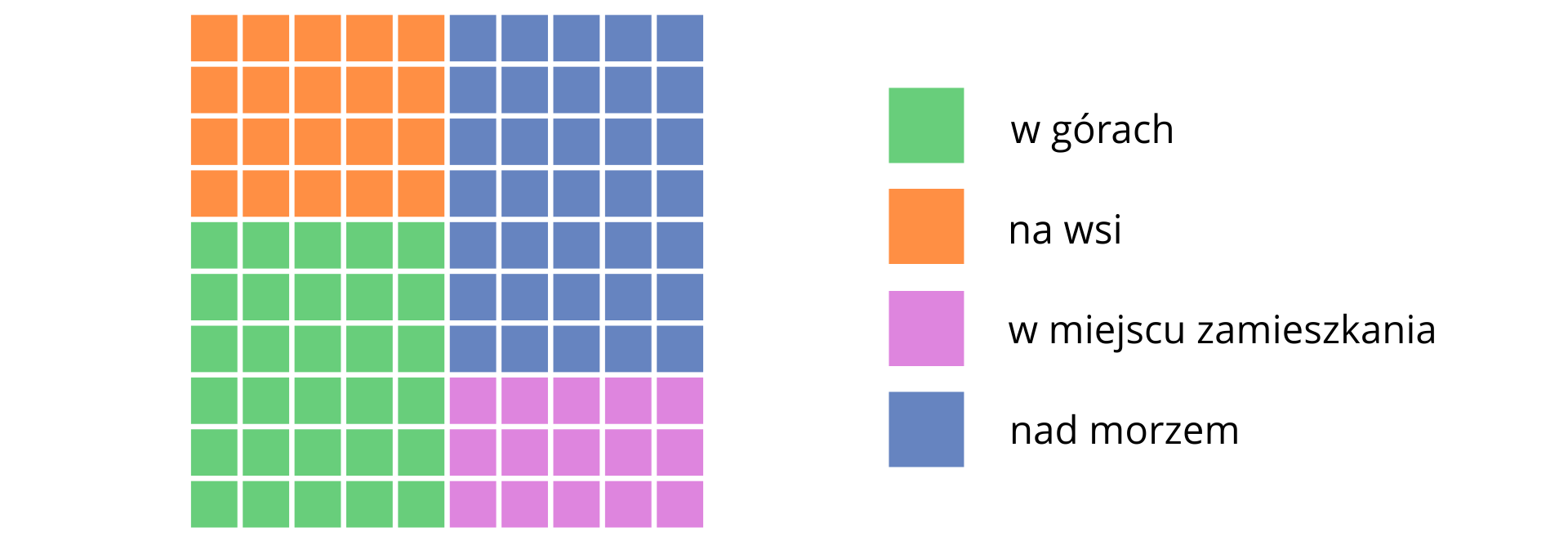
Zapytano uczniów w jaki sposób spędzą wakacje. Można było wskazać tylko jedną odpowiedź. Wyniki przedstawiono na wykresie prostokątnym.
Uczniowie biorący udział w finale konkursu Bystrzaki na start, mogli otrzymać najwięcej punktów. W tabeli zamieszczono wyniki finalistów.
Liczba punktów | Liczba uczniów |
|---|---|
Marzena zebrała w pobliskich cukierniach dane na temat cen pączków w styczniu i w marcu.
Uzyskane informacje przedstawiła w tabeli.
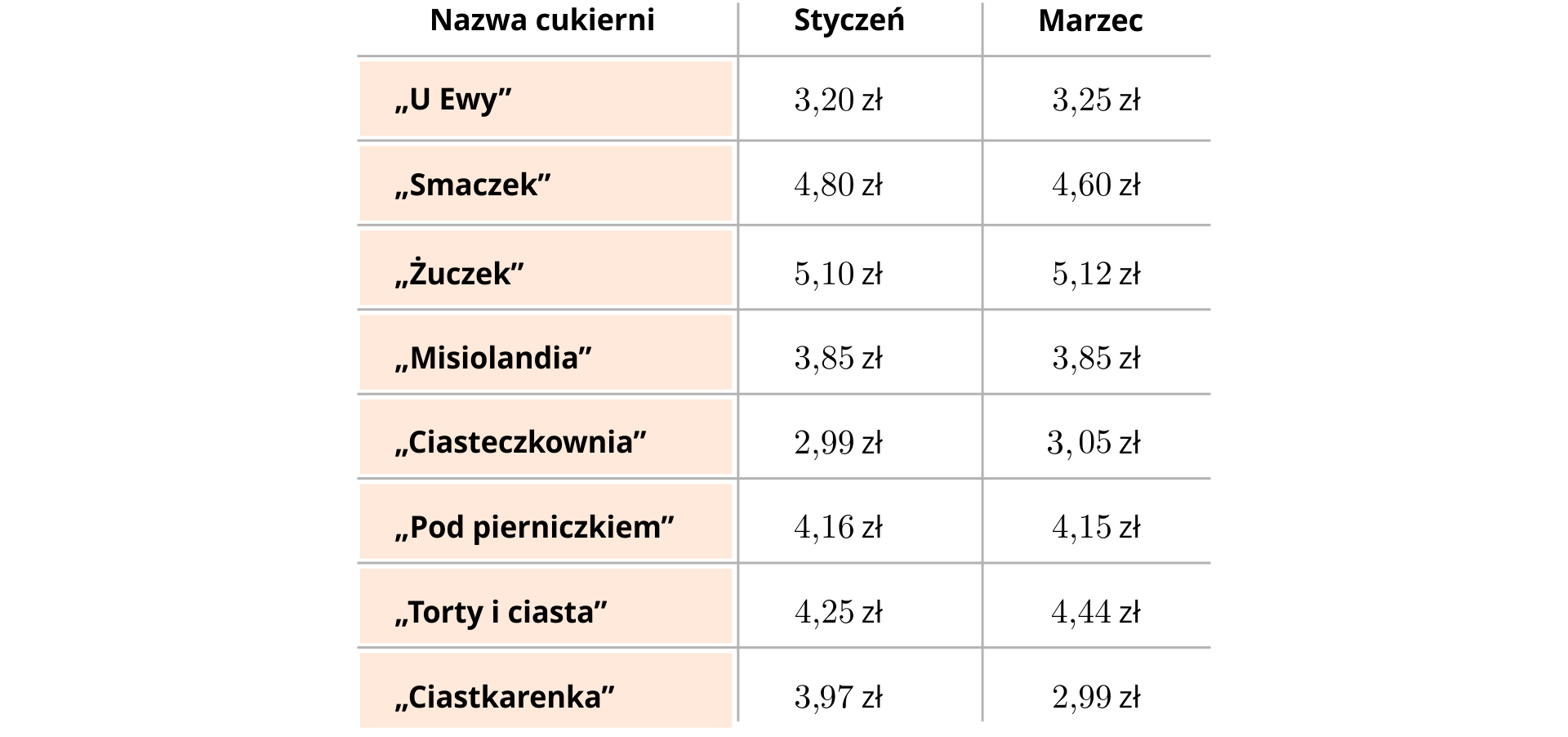
Uzyskane informacje przedstawiła w poniższej tabeli.
Nazwa cukierni | Styczeń | Marzec |
|---|---|---|
„U Ewy” | ||
„Smaczek” | ||
„Żuczek” | ||
„Misiolandia” | ||
„Ciasteczkownia” | ||
„Pod pierniczkiem” | ||
„Torty i ciasta” | ||
„Ciastkarenka” |
Marek na wykresie punktowym zaznaczył, ile godzin dziennie przeznaczył na naukę w tym tygodniu.
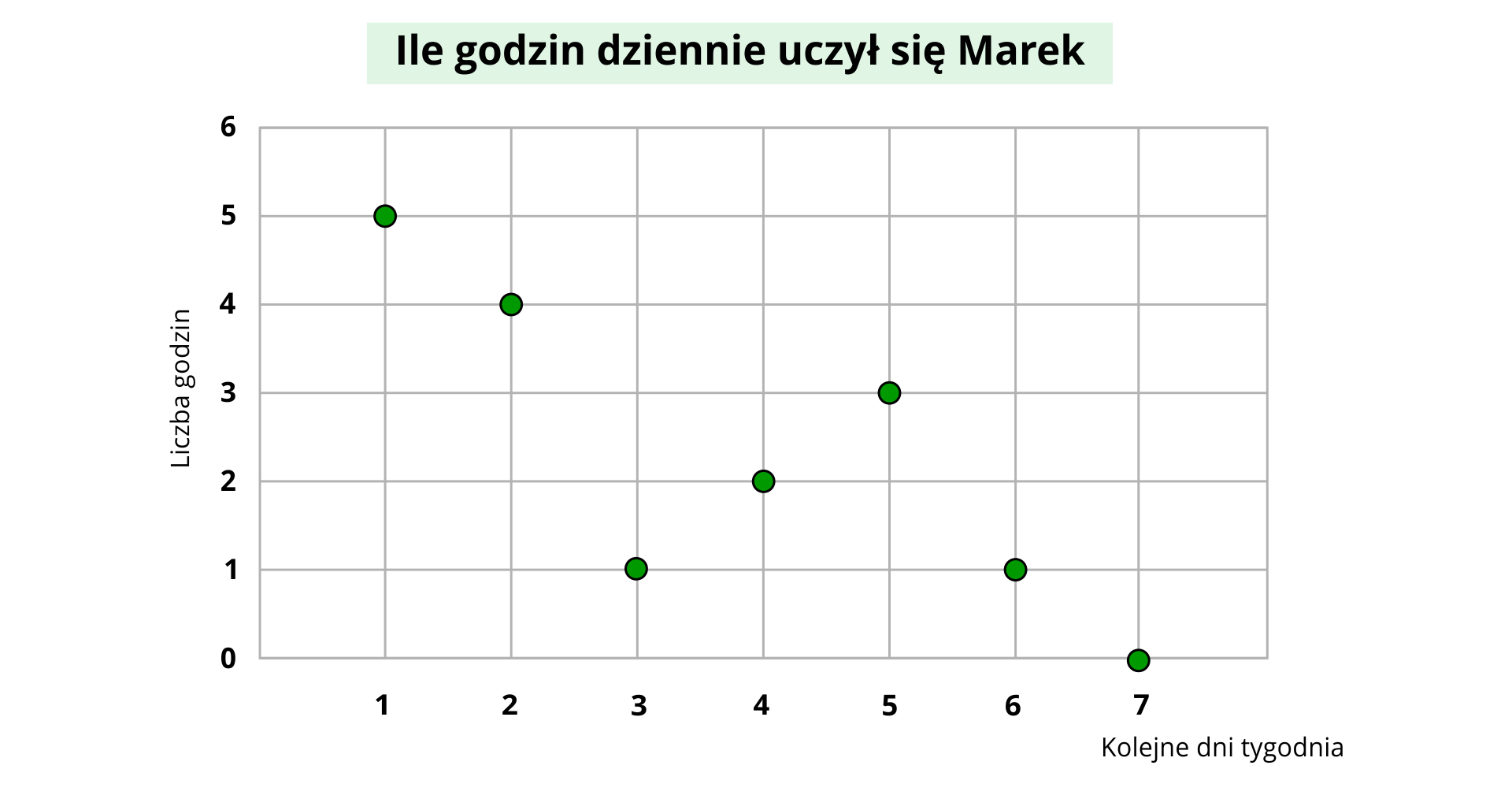
Korzystając z wykresu, odpowiedz na pytania.
Którego dnia Marek uczył się najdłużej?
Ile łącznie godzin w tym tygodniu Marek przeznaczył na naukę?
Którego dnia Marek uczył się przez dwie godziny?
O ile godzin dłużej Marek uczył się we wtorek niż w sobotę?
Którego dnia Marek nie uczył się wcale?
Pierwszy autobus linii nr odjeżdża z przystanku o godzinie , a ostatni o godzinie .
Rozkład jazdy autobusu linii nr .

Ania przyszła na przystanek o godzinie . Jak długo musi czekać na najbliższy autobus?
Piotrek z domu do autobusu idzie minut. Tym razem jednak spotkał kolegę i rozmawiał z nim minut, a następnie wszedł do sklepu i kupił bułki, co zajęło mu dodatkowo minut. Czy zdążył na ostatni autobus, jeśli z domu wyszedł o ?
Słownik
dział statystyki zajmujący się gromadzeniem, opracowaniem i prezentacją oraz analizą danych statystycznych.
zbiór informacji statystycznych uporządkowanych według określonego kryterium.
Bibliografia
Rumsey Deborah J., (2022), Statystyka dla bystrzaków, Gliwice: Wydawnictwo Dla bystrzaków.