Okrąg opisany na trójkącie

W tym materiale dowiesz się:

  • jak wyznaczamy środek okręgu opisanego na trójkącie,

  • jaka jest zależność pomiędzy rodzajem trójkąta, a miejscem położenia środka okręgu,

  • jakie praktyczne zastosowanie może mieć umiejętność wyznaczania środka okręgu opisanego na trójkącie.

1
Przykład 1

Wyobraźmy sobie, że w pewnym powiecie należy wybudować stację benzynową w takim miejscu, aby znajdowała się w takiej samej odległości od każdej z  miejscowości A, B i C.

Zakładamy przy tym, że w pobliżu tych miejscowości nie ma jeziora, nie płynie rzeka, ani nie znajdują się żadne inne przeszkody uniemożliwiające wybudowanie w danym punkcie stacji benzynowej.

Zastanów się, jak znaleźć miejsce, w którym należy wybudować stację benzynową.

Jeśli nie masz pomysłu – zastosuj nasze wskazówki zawarte w aplecie „Stacja benzynowa” zamieszczonym poniżej.

R83QqTZdSGWNP1
Aplet pokazuje jak znaleźć miejsce, w którym należy wybudować stację benzynową tak, aby znajdowała się w takiej samej odległości od każdej z miejscowości A, B i C . Ile istnieje takich miejsc, w których stacja benzynowa będzie oddalona o tą samą odległość od miejscowości A i B: jedno, dwa czy nieskończenie wiele? Miejsce, w którym można wybudować stację, powinno znaleźć się na symetralnej odcinka AB. Konstruujemy tę symetralną. Czy już wiesz, ile stacji spełniających warunki, można zbudować dla miejscowości A i B? Prawidłowa odpowiedź to nieskończenie wiele. W podobny sposób znajdujemy miejsca, w których można zbudować stację dla miejscowości B i C - konstruujemy symetralną odcinka BC. Analogicznie postępujemy dla miejscowości C i A - konstruujemy symetralną odcinka AC. Wszystkie trzy symetralne przecinają się w jednym punkcie O. Punkt O leży w jednakowej odległości punktów A, B oraz C.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Psy6zSOgk

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Co zauważasz? Gdzie twoim zdaniem powinna stanąć stacja benzynowa?

Jeśli uważasz, że w punkcie przecięcia narysowanych prostych, uzasadnij swoje przypuszczenia.

Uzasadnienie:

Symetralna odcinka jest prostą będącą zbiorem punktów równo oddalonych od obu końców odcinka. Jeśli rozważymy trójkąt ABC, to otrzymane proste są symetralnymi boków tego trójkąta. Symetralne te przecięły się w jednym punkcie, który leży na symetralnej odcinka AB, na symetralnej odcinka BC i na symetralnej odcinka CA. Zatem leży w tej samej odległości odpowiednio od punktów A i B oraz B i C oraz C i A.

Zapamiętaj!

Symetralne boków trójkąta przecinają się w jednym punkcie.

Punkt ten jest jednakowo odległy od wierzchołków tego trójkąta.

RCDdAK6Dk1rnv1
Rysunek trójkąta A B C. Symetralne boków przecinają się w punkcie O. Odległość punktu O od wierzchołków trójkąta ma długość d.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 2

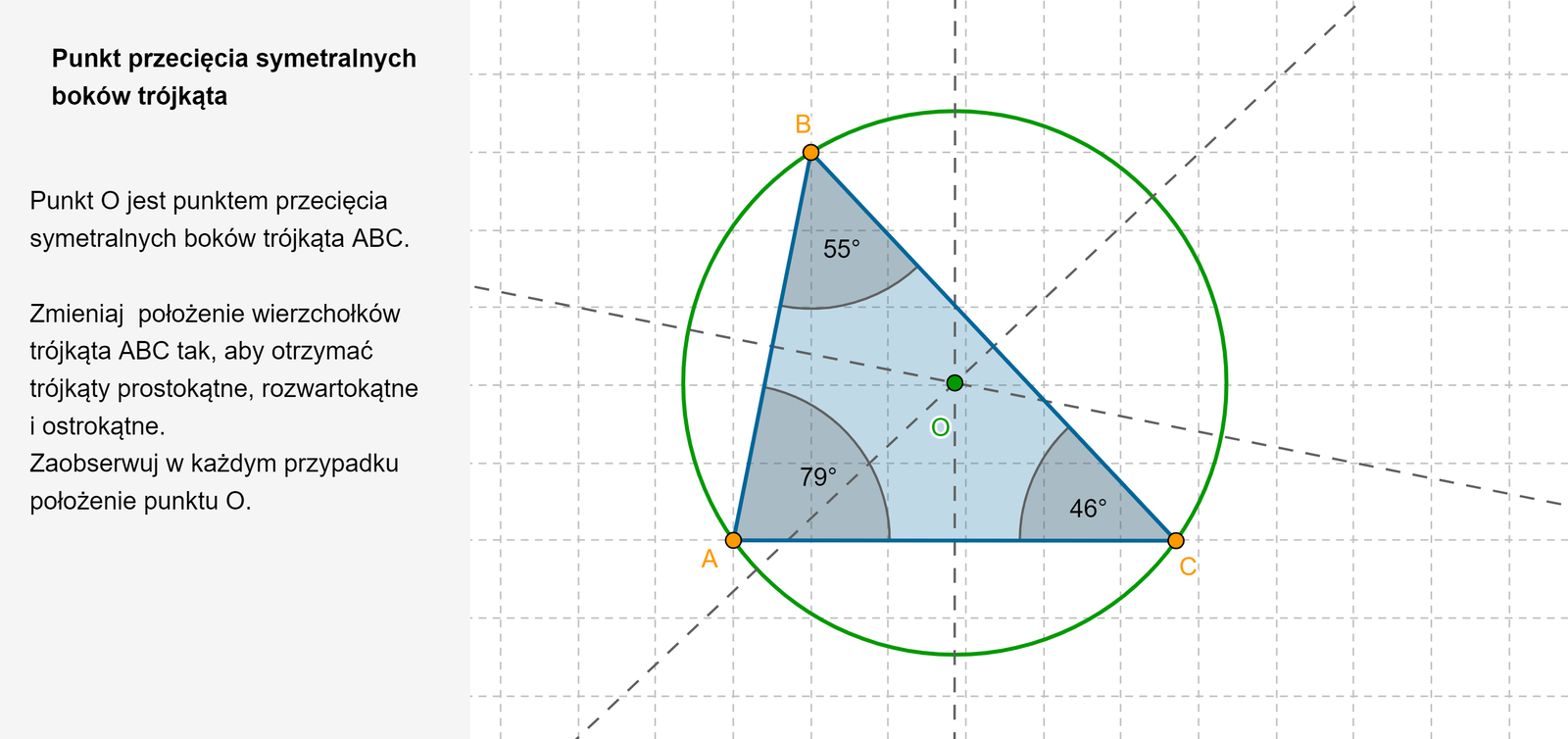
Sprawdzimy, gdzie znajduje się punkt przecięcia symetralnych boków trójkąta, w zależności od rodzaju tego trójkąta.

R1085AUPY75yQ1
Aplet pokazuje trójkąt A B C. Punkt O jest punktem przecięcia symetralnych boków trójkąta A B C. Zmieniając położenie wierzchołków otrzymujemy trójkąt ostrokątny, trójkąt prostokątny lub trójkąt rozwartokątny. Zauważamy, że dla trójkątów ostrokątnych środek okręgu opisanego na trójkącie leży wewnątrz trójkąta A B C. Dla trójkąta prostokątnego środek okręgu opisanego na trójkącie jest środkiem najdłuższego boku trójkąta A B C. Dla trójkątów rozwartokątnych okręgu opisanego na trójkącie leży na zewnątrz trójkąta A B C.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Psy6zSOgk

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  • Czy punkt przecięcia symetralnych może leżeć na jednym z boków trójkąta? Jeśli tak, to jaki to rodzaj trójkąta?

  • Czy punkt ten może leżeć poza trójkątem? Jeśli tak, to jaki to rodzaj trójkąta?

  • Czy punkt ten może należeć do wnętrza trójkąta? Jeśli tak, to jaki to rodzaj trójkąta?

Zapamiętaj!

Symetralne boków trójkąta

  • ostrokątnego przecinają się w punkcie należącym do wnętrza tego trójkąta,

  • prostokątnego przecinają się w punkcie będącym środkiem najdłuższego boku tego trójkąta,

  • rozwartokątnego przecinają się w punkcie leżącym poza trójkątem.

    R57mPwLCDh9We1
    Grafika przedstawia trzy trójkąty. Pierwszy trójkąt to trójkąt ostrokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się wewnątrz trójkąta. Drugi trójkąt to trójkąt prostokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się w połowie przeciwprostokątnej tego trójkąta. Trzeci trójkąt to trójkąt rozwartokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się na zewnątrz trójkąta.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Okrąg opisany na trójkącie
Definicja: Okrąg opisany na trójkącie

Jeżeli na okręgu leżą wszystkie wierzchołki trójkąta, to taki okrąg nazywamy okręgiem opisanym na trójkącie. O trójkącie mówimy, że jest wpisany w okrąg.

R1BvoOWepU7yx1
Rysunek okręgu o środku w punkcie O opisanego na trójkącie. Odległość punktu O od wszystkich wierzchołków trójkąta ma długość d.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 3

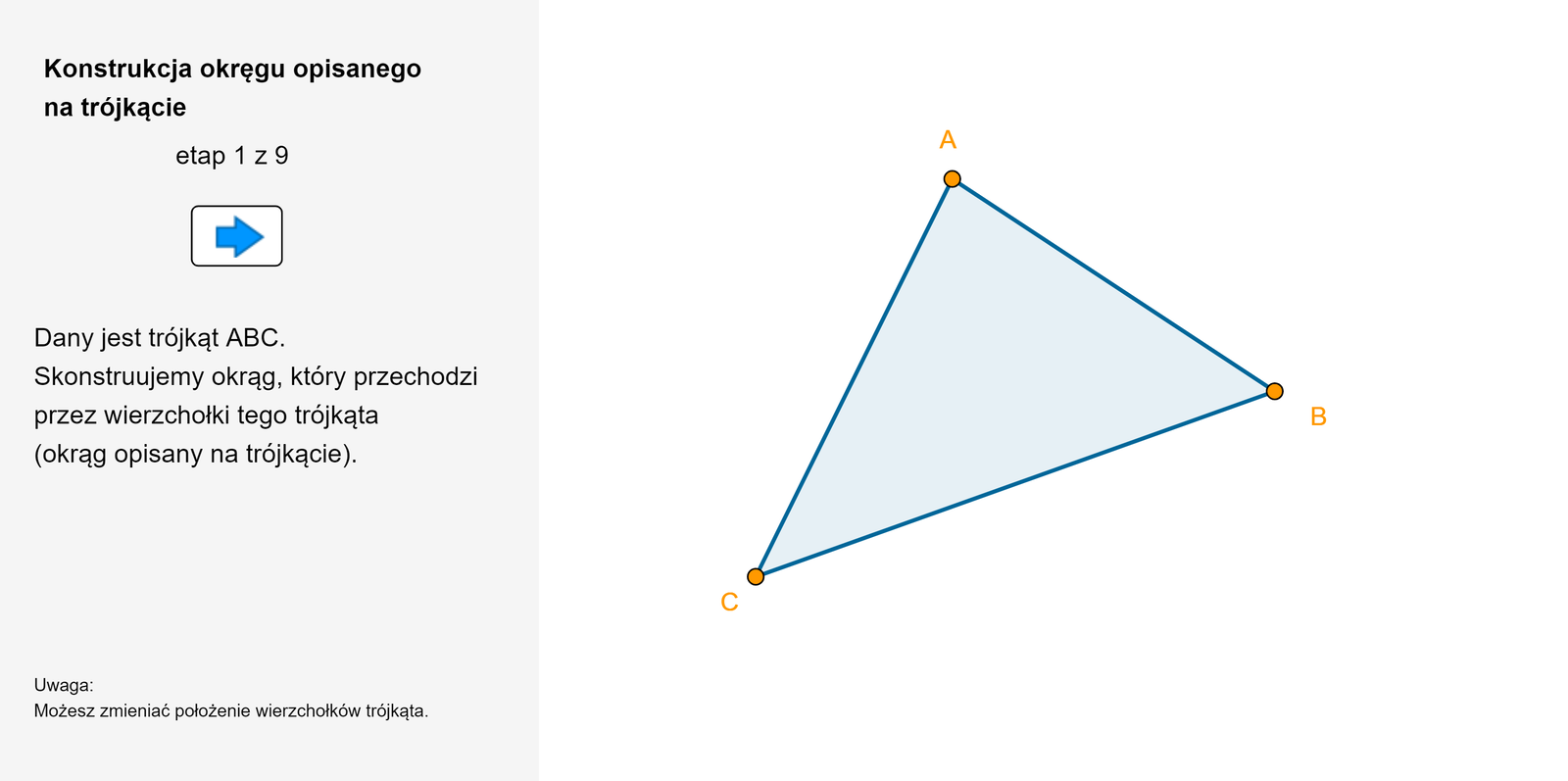
Skonstruujemy okrąg opisany na trójkącie.

Wiemy już, że środek okręgu musi leżeć w tej samej odległości od wierzchołków trójkąta. Leży zatem na przecięciu symetralnych boków trójkąta.

R1MFwqNjmSPov1
Aplet pokazuje w dziewięciu krokach konstrukcję okręgu opisanego na trójkącie. Dany jest trójkąt A B C. Konstruujemy okrąg, który będzie przechodził przez wierzchołki tego trójkąta. Konstruujemy symetralną odcinka AB i symetralną odcinka BC. Punkt przecięcia tych symetralnych wyznacza środek okręgu opisanego na tym trójkącie. Okrąg o środku O, przechodzący przez dowolny z wierzchołków trójkąta, jest okręgiem opisanym na trójkącie A B C. Uzasadnienie prawidłowości konstrukcji: Ponieważ punkt O leży na symetralnej boku AB, więc jest równo odległy od wierzchołków A i B. Ponieważ punkt O leży na symetralnej boku BC, więc jest równo odległy od wierzchołków B i C. Prowadzimy trzecią symetralną - symetralną boku AC. Czy punkt O leży na tej symetralnej? Ponieważ długość OA = OB oraz OB = OC, więc również OA = OC, a to oznacza, że punkt O leży na symetralnej boku AC.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Psy6zSOgk

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Okrąg opisany na trójkącie
Twierdzenie: Okrąg opisany na trójkącie

Na każdym trójkącie można opisać okrąg. Środek tego okręgu leży na przecięciu symetralnych boków tego trójkąta.

Zastanówmy się teraz, gdzie może leżeć środek okręgu opisanego na trójkącie.
W tym celu przypomnijmy sobie rozważania na temat położenia punktu przecięcia symetralnych trójkąta. Zwróć uwagę na poniższą ilustrację, na której przedstawiono wszystkie możliwości położenia środka okręgu opisanego na trójkącie.

R1cVYq6fSYHIW1
Grafika przedstawia trzy trójkąty z opisanymi na nich okręgami. Pierwszy trójkąt to trójkąt ostrokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się wewnątrz trójkąta i wyznacza środek okręgu opisanego na tym trójkącie. Drugi trójkąt to trójkąt prostokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się w połowie przeciwprostokątnej tego trójkąta i wyznacza środek okręgu opisanego na tym trójkącie. Trzeci trójkąt to trójkąt rozwartokątny z wyznaczonymi trzema symetralnymi swoich boków, punkt przecięcia wszystkich symetralnych znajduje się na zewnątrz trójkąta i wyznacza środek okręgu opisanego na tym trójkącie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RMZv0iH6eFVUI
Ćwiczenie 1
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej tak, aby poprawne było uzasadnienie poniższej tezy. Na każdym trójkącie można opisać okrąg.
Uzasadnienie:
W każdym trójkącie możemy wyznaczyć 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne jego boków i punkt przecięcia tych 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne będzie jednakowo odległy od każdego wierzchołka trójkąta.

Punkt przecięcia 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne jest wtedy środkiem okręgu, a jego 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne jest odległość między punktem przecięcia 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne i 1. symetralnych, 2. dwusiecznych, 3. dowolnym wierzchołkiem, 4. dowolnym środkiem podstawy, 5. symetralnych, 6. dwusiecznych, 7. promieniem, 8. dwusiecznych, 9. dwusieczne, 10. symetralnych, 11. średnicą, 12. symetralne.

Możemy tak postąpić w każdym przypadku, więc na każdym trójkącie można opisać okrąg.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1DgSOgeBTx8B1
Ćwiczenie 2
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Środkiem okręgu opisanego na trójkącie jest punkt przecięcia symetralnych boków tego trójkąta., 2. Środkiem okręgu opisanego na trójkącie jest punkt przecięcia dwusiecznych kątów tego trójkąta., 3. Na każdym trójkącie można opisać okrąg.

  • Środkiem okręgu opisanego na trójkącie jest punkt przecięcia symetralnych boków tego trójkąta.
  • Środkiem okręgu opisanego na trójkącie jest punkt przecięcia dwusiecznych kątów tego trójkąta.
  • Na każdym trójkącie można opisać okrąg.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rac1bCoRcLLjp1
Ćwiczenie 3
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Środek okręgu opisanego na trójkącie ostrokątnym leży 1. na zewnątrz, 2. wewnątrz trójkąta, 3. poza trójkątem, 4. trzy, 5. dwie, 6. przyprostokątnej, 7. we wnętrzu, 8. dowolnym boku, 9. na jednym z boków tego trójkąta., 10. przeciwprostokątnej tego trójkąta.Środek okręgu opisanego na trójkącie prostokątnym leży na 1. na zewnątrz, 2. wewnątrz trójkąta, 3. poza trójkątem, 4. trzy, 5. dwie, 6. przyprostokątnej, 7. we wnętrzu, 8. dowolnym boku, 9. na jednym z boków tego trójkąta., 10. przeciwprostokątnej tego trójkąta i dzieli ten bok na 1. na zewnątrz, 2. wewnątrz trójkąta, 3. poza trójkątem, 4. trzy, 5. dwie, 6. przyprostokątnej, 7. we wnętrzu, 8. dowolnym boku, 9. na jednym z boków tego trójkąta., 10. przeciwprostokątnej równe części.Środek okręgu opisanego na trójkącie rozwartokątnym leży 1. na zewnątrz, 2. wewnątrz trójkąta, 3. poza trójkątem, 4. trzy, 5. dwie, 6. przyprostokątnej, 7. we wnętrzu, 8. dowolnym boku, 9. na jednym z boków tego trójkąta., 10. przeciwprostokątnej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RZREPvPz25m8Z2
Ćwiczenie 4
Połącz w pary trójkąt i położenie środka okręgu opisanego na tym trójkącie. trójkąt równoramienny o kącie między ramionami wynoszącym 100° Możliwe odpowiedzi: 1. na najdłuższym z boków, 2. we wnętrzu trójkąta, 3. poza trójkątem trójkąt równoboczny o długości boku równym 3 cm Możliwe odpowiedzi: 1. na najdłuższym z boków, 2. we wnętrzu trójkąta, 3. poza trójkątem trójkąt o bokach długości 4 cm, 4 cm i 5 cm Możliwe odpowiedzi: 1. na najdłuższym z boków, 2. we wnętrzu trójkąta, 3. poza trójkątem
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 5
Ra5MlkkpFL1Lb2
Promień okręgu opisanego na trójkącie prostokątnym równoramiennym ma długość 10 cm. Oblicz, jaką długość ma odcinek łączący wierzchołek kąta prostego ze środkiem przeciwprostokątnej. Uzupełnij poniższe zdanie, przeciągając w lukę odpowiednią liczbę. Odcinek łączący wierzchołek kąta prostego ze środkiem przeciwprostokątnej ma długość 1. 15, 2. 10, 3. 25, 4. 5, 5. 20 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1YzwPo4c4Pxv2
Ćwiczenie 6
W trójkącie równoramiennym jeden z kątów ma miarę 80°. Czy środek okręgu opisanego na tym trójkącie leży wewnątrz tego trójkąta? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Tak, środek okręgu opisanego na tym trójkącie leży wewnątrz tego trójkąta., 2. Nie, środek okręgu opisanego na tym trójkącie nie leży wewnątrz tego trójkąta., 3. Tak, środek okręgu opisanego na tym trójkącie leży w jednym z wierzchołków tego trójkąta., 4. Nie, środek okręgu opisanego na tym trójkącie leży na jednym z boków tego trójkąta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1JOqHuDj6teY2
Ćwiczenie 7
W trójkącie suma miar dwóch kątów wynosi 80°. Czy środek okręgu opisanego na tym trójkącie leży wewnątrz tego trójkąta? Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. Nie, bo trójkąt jest rozwartokątny., 2. Tak, bo trójkąt jest ostrokątny.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
3
Ćwiczenie 8

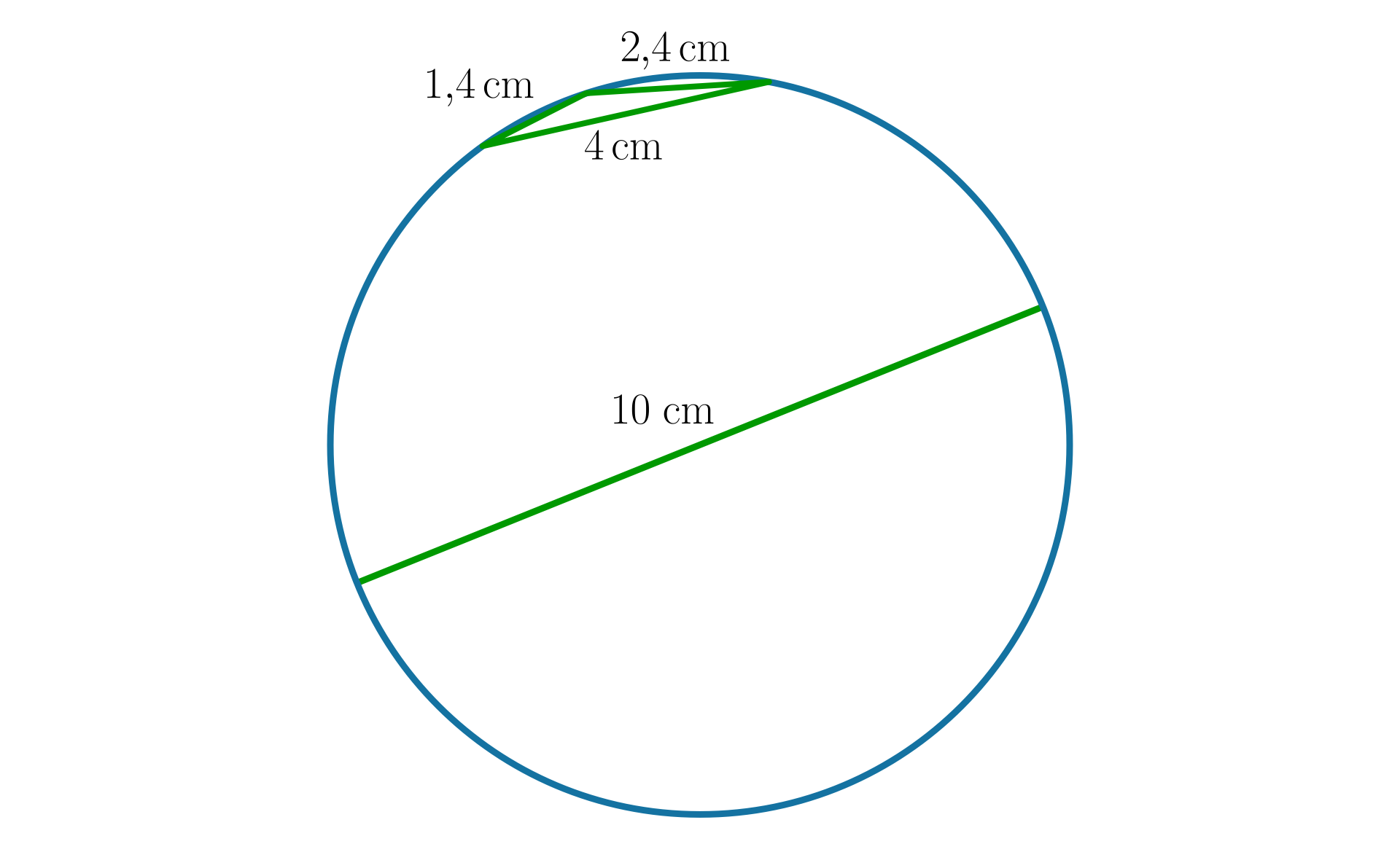
Skonstruuj dowolny trójkąt, którego obwód jest mniejszy od średnicy okręgu opisanego na tym trójkącie.

RjqKBkdCzMaUB
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Opisz konstrukcję trójkąta, którego obwód jest mniejszy od średnicy okręgu opisanego na tym trójkącie.

3
Ćwiczenie 9

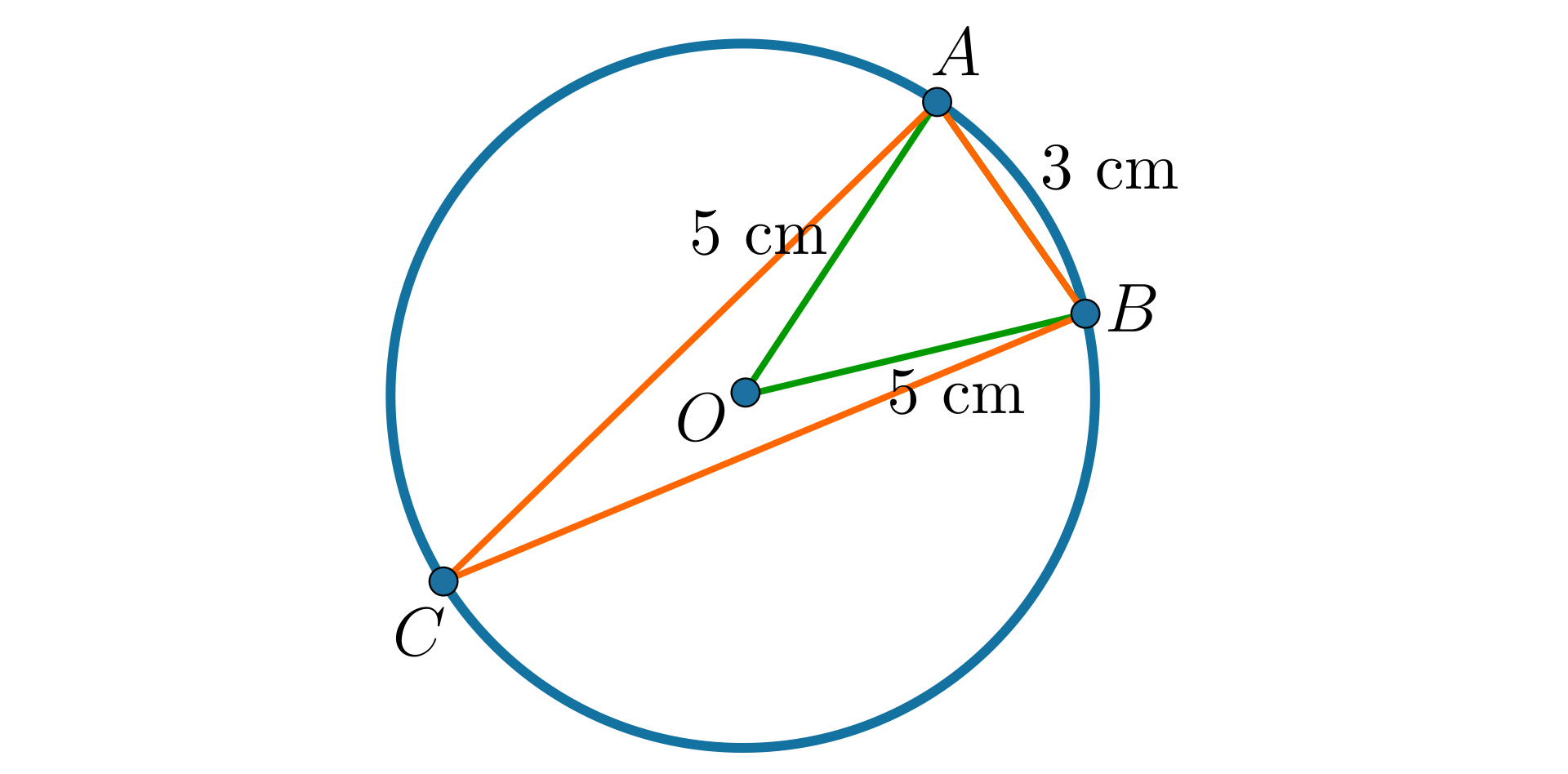
Zbuduj trójkąt, którego jeden bok ma długość 3 cm, a odległość środka okręgu opisanego na tym trójkącie od jednego z jego wierzchołków wynosi 5 cm.

RcMvJybiLEgS3
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Opisz budowę trójkąta, którego jeden bok ma długość 3 cm, a odległość środka okręgu opisanego na tym trójkącie od jednego z jego wierzchołków wynosi 5 cm.

R1Qu5afzDIn0Z3
Ćwiczenie 10
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Środek okręgu opisanego na trójkącie równobocznym jest punktem przecięcia wysokości tego trójkąta., 2. Dla dowolnych trzech punktów niewspółliniowych można narysować okrąg, który przechodzi przez te punkty., 3. Każdy bok trójkąta prostokątnego wpisanego w okrąg jest krótszy od średnicy tego okręgu., 4. Każdy bok trójkąta rozwartokątnego wpisanego w okrąg jest krótszy od średnicy tego okręgu.

  • Środek okręgu opisanego na trójkącie równobocznym jest punktem przecięcia wysokości tego trójkąta.
  • Dla dowolnych trzech punktów niewspółliniowych można narysować okrąg, który przechodzi przez te punkty.
  • Każdy bok trójkąta rozwartokątnego wpisanego w okrąg jest krótszy od średnicy tego okręgu
  • Każdy bok trójkąta prostokątnego wpisanego w okrąg jest krótszy od średnicy tego okręgu.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1U6HRXc4VrFu3
Ćwiczenie 11
Uzupełnij odpowiedzi, przeciągając w luki odpowiednie słowa. Jeśli środek okręgu opisanego na trójkącie leży na zewnątrz trójkąta, to trójkąt ten jest 1. rozwartokątny, 2. ostrokątny, 3. prostokątny.Jeśli środek okręgu opisanego na trójkącie leży wewnątrz trójkąta, to trójkąt ten jest 1. rozwartokątny, 2. ostrokątny, 3. prostokątny.Jeśli środek okręgu opisanego na trójkącie nie leży na brzegu trójkąta, to trójkąt ten nie jest 1. rozwartokątny, 2. ostrokątny, 3. prostokątny.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.