Określanie monotoniczności funkcji - zadania

W tym materiale znajdziesz zadania dotyczące monotoniczności funkcji. Jeżeli chcesz sobie przypomnieć podstawowe wiadomości na temat monotoniczności, zajrzyj do materiału Monotoniczność funkcjiDRBFgBGnPMonotoniczność funkcji.

R1Wi6FOWyA3Rg1
Ćwiczenie 1
Uzupełnij poniższe zdania tak, aby były zdaniami prawdziwymi. Kliknij w lukę aby rozwinąć listę i wybierz właściwą odpowiedź. Mówimy, że funkcja f określona w przedziale ⟨a,b⟩ jest 1. nierosnąca, 2. rosnąca, 3. malejąca, 4. stała, 5. niemalejąca w przedziale ⟨a,b⟩, jeżeli dla dowolnych x1,x2∈⟨a,b⟩ takich, że x1<x2 zachodzi warunek fx1>fx2.Mówimy, że funkcja f określona w przedziale ⟨a,b⟩ jest 1. nierosnąca, 2. rosnąca, 3. malejąca, 4. stała, 5. niemalejąca w przedziale ⟨a,b⟩, jeżeli dla dowolnych x1,x2∈⟨a,b⟩ takich, że x1<x2 zachodzi warunek fx1<fx2.Mówimy, że funkcja f określona w przedziale ⟨a,b⟩ jest 1. nierosnąca, 2. rosnąca, 3. malejąca, 4. stała, 5. niemalejąca w przedziale ⟨a,b⟩, jeżeli dla dowolnych x1,x2∈⟨a,b⟩ takich, że x1<x2 zachodzi warunek fx1=fx2.Mówimy, że funkcja f określona w przedziale ⟨a,b⟩ jest 1. nierosnąca, 2. rosnąca, 3. malejąca, 4. stała, 5. niemalejąca w przedziale ⟨a,b⟩, jeżeli dla dowolnych x1,x2∈⟨a,b⟩ takich, że x1<x2 zachodzi warunek fx1≥fx2.Mówimy, że funkcja f określona w przedziale ⟨a,b⟩ jest 1. nierosnąca, 2. rosnąca, 3. malejąca, 4. stała, 5. niemalejąca w przedziale ⟨a,b⟩, jeżeli dla dowolnych x1,x2∈⟨a,b⟩ takich, że x1<x2 zachodzi warunek fx1≤fx2.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rz01NDmvecF801
Ćwiczenie 2
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Jeżeli funkcja jest malejąca w przedziale ⟨a,b⟩, to jest nierosnąca w przedziale ⟨a,b⟩., 2. Jeżeli funkcja jest rosnąca w przedziale ⟨a,b⟩, to jest niemalejąca w przedziale ⟨a,b⟩., 3. Istnieje funkcja, która jest jednocześnie malejąca w przedziale ⟨a,b⟩ i rosnąca w przedziale ⟨a,b⟩., 4. Funkcja stała w przedziale ⟨a,b⟩ nie jest ani malejąca, ani rosnąca w przedziale ⟨a,b⟩.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 3

Zapoznaj się z wykresem poniższej funkcji.

R13enLm9APlFP
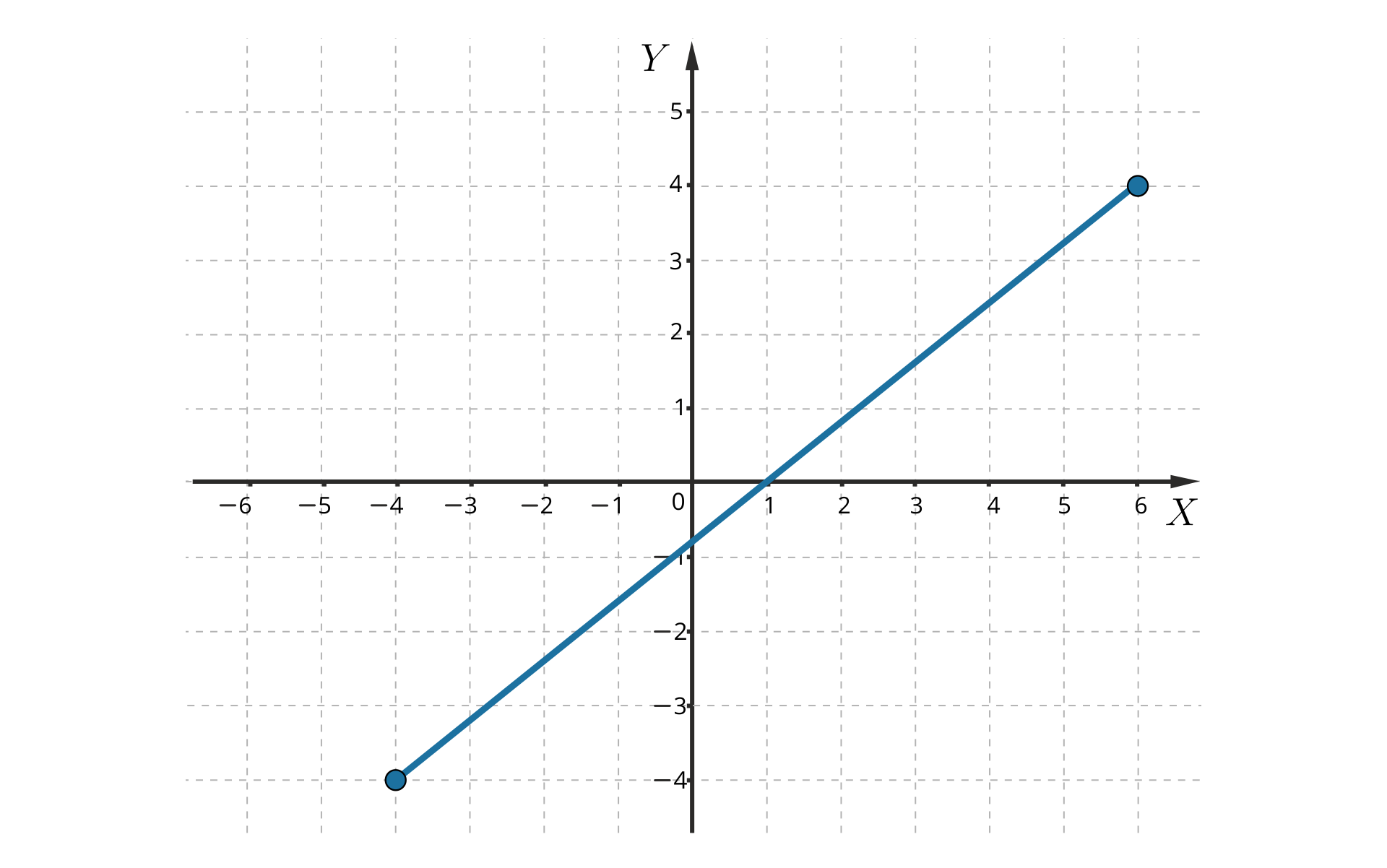
Rysunek przedstawia wykres funkcji, który jest odcinkiem o początku w punkcie -4,-4 i końcu w punkcie 6,4.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RqFkeJrSrMcRg
Uzupełnij poniższe zdanie tak, aby było zdaniem prawdziwym. Kliknij w lukę, aby rozwinąć listę i wybierz odpowiednią liczbę. Maksymalnym przedziałem, w którym funkcja jest rosnąca jest 1. ⟨-4,6⟩, 2. ⟨-3,7⟩, 3. ⟨-4,5⟩, 4. ⟨-6,4⟩, 5. ⟨-5,6⟩.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 4

Zapoznaj się z wykresem poniższej funkcji.

R1G5PEPyrtB71
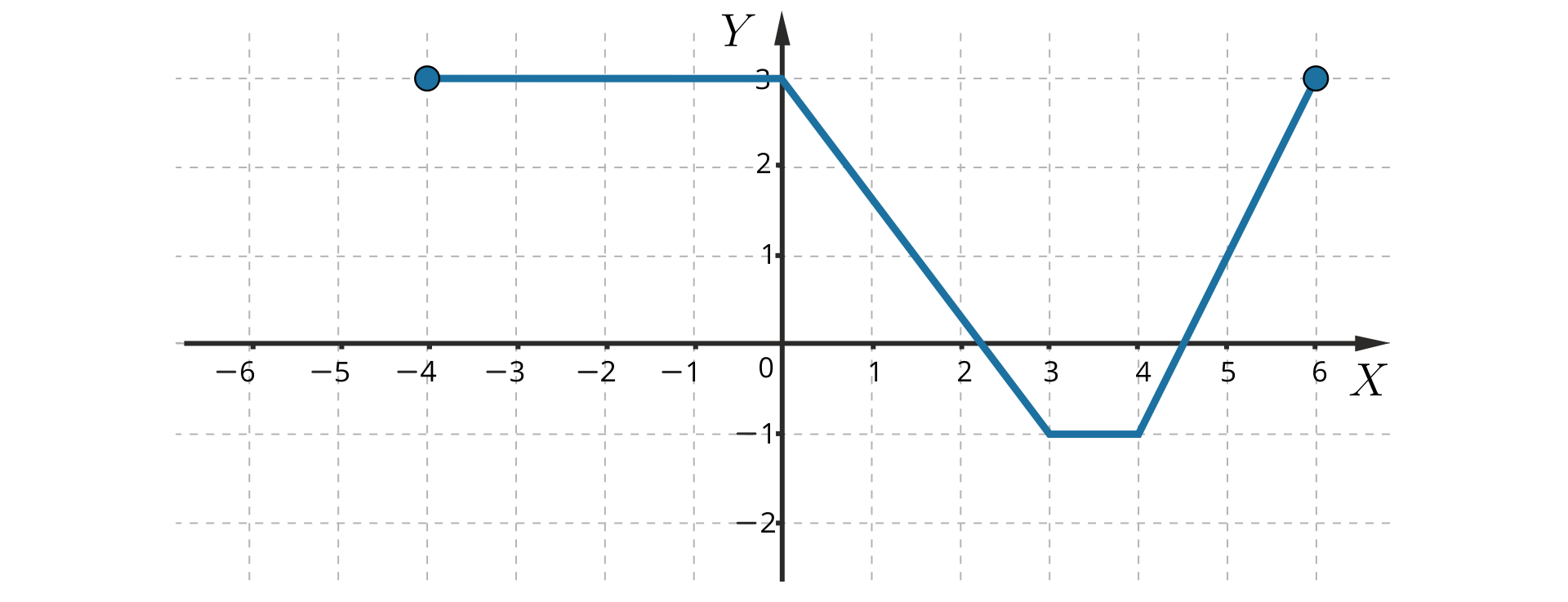
Rysunek przedstawia wykres funkcji składający się z czterech fragmentów. Pierwszy fragment od lewej to odcinek o początku w punkcie -4,3 i końcu w punkcie 0,3, drugi fragment od lewej to odcinek o początku w punkcie 0,3 i końcu w punkcie 3,-1, trzeci fragment od lewej to odcinek o początku w punkcie 3,-1 i końcu w punkcie 4,-1, czwarty fragment od lewej to odcinek o początku w punkcie 4,-1 i końcu w punkcie 6,3.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RD7N6AmP6dQW6
Zaznacz zdanie prawdziwe. Możliwe odpowiedzi: 1. Funkcja jest nierosnąca w przedziale ⟨-4,4⟩., 2. Funkcja jest niemalejąca w przedziale ⟨-4,4⟩., 3. Funkcja jest rosnąca w przedziale ⟨3,6⟩., 4. Funkcja jest nierosnąca w całej swojej dziedzinie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 5

Zapoznaj się z wykresem poniższej funkcji.

R1DK6wF9RlbdF
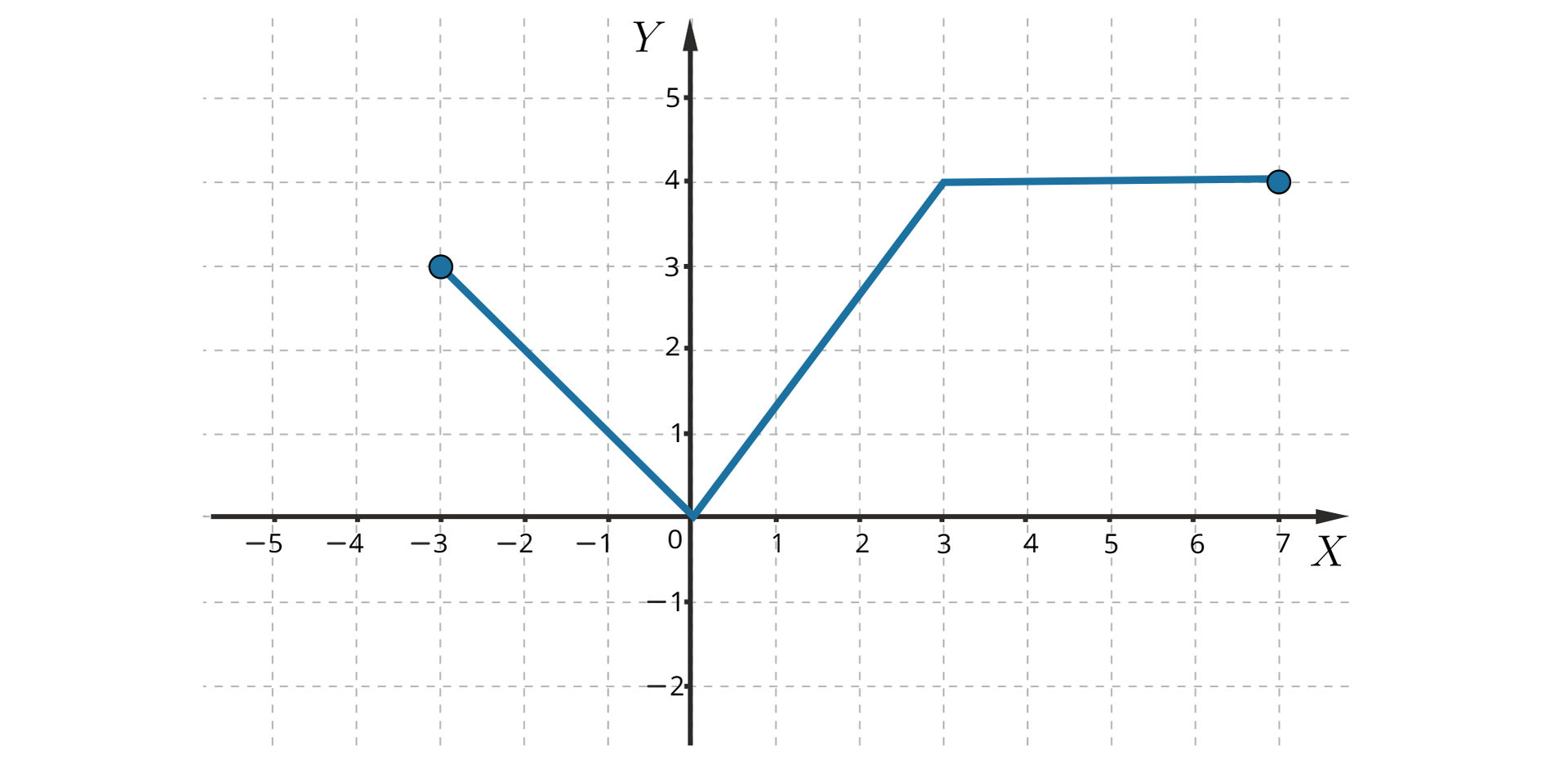
Rysunek przedstawia wykres funkcji składający się z trzech fragmentów. Pierwszy fragment od lewej to odcinek o początku w punkcie -3,3 i końcu w punkcie 0,0, drugi fragment od lewej jest odcinkiem o początku w punkcie 0,0 i końcu w punkcie 3,4, trzeci fragment od lewej jest odcinkiem o początku w punkcie 3,4 i końcu w punkcie 7,4.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RIm6vP2UHdSwS
Uzupełnij luki w zdaniach, wpisując odpowiednie liczby. Maksymalnym przedziałem, w którym funkcja jest malejąca jest ⟨Tu uzupełnij,Tu uzupełnij⟩.Maksymalnym przedziałem, w którym funkcja jest rosnąca jest ⟨Tu uzupełnij,Tu uzupełnij⟩.Maksymalnym przedziałem, w którym funkcja jest stała jest ⟨Tu uzupełnij,Tu uzupełnij⟩.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
3
Ćwiczenie 6

Zapoznaj się z wykresem poniższej funkcji.

R1XfimZPpHWjv
Rysunek przedstawia wykres funkcji składający się z trzech fragmentów. Pierwszy fragment od lewej to odcinek o początku w punkcie -5,-3 i końcu w punkcie -3,2, drugi fragment od lewej jest odcinkiem o początku w punkcie -3,2 i końcu w punkcie 4,2, trzeci fragment od lewej jest odcinkiem o początku w punkcie 4,2 i końcu w punkcie 7,-3&lt;\math&gt;.
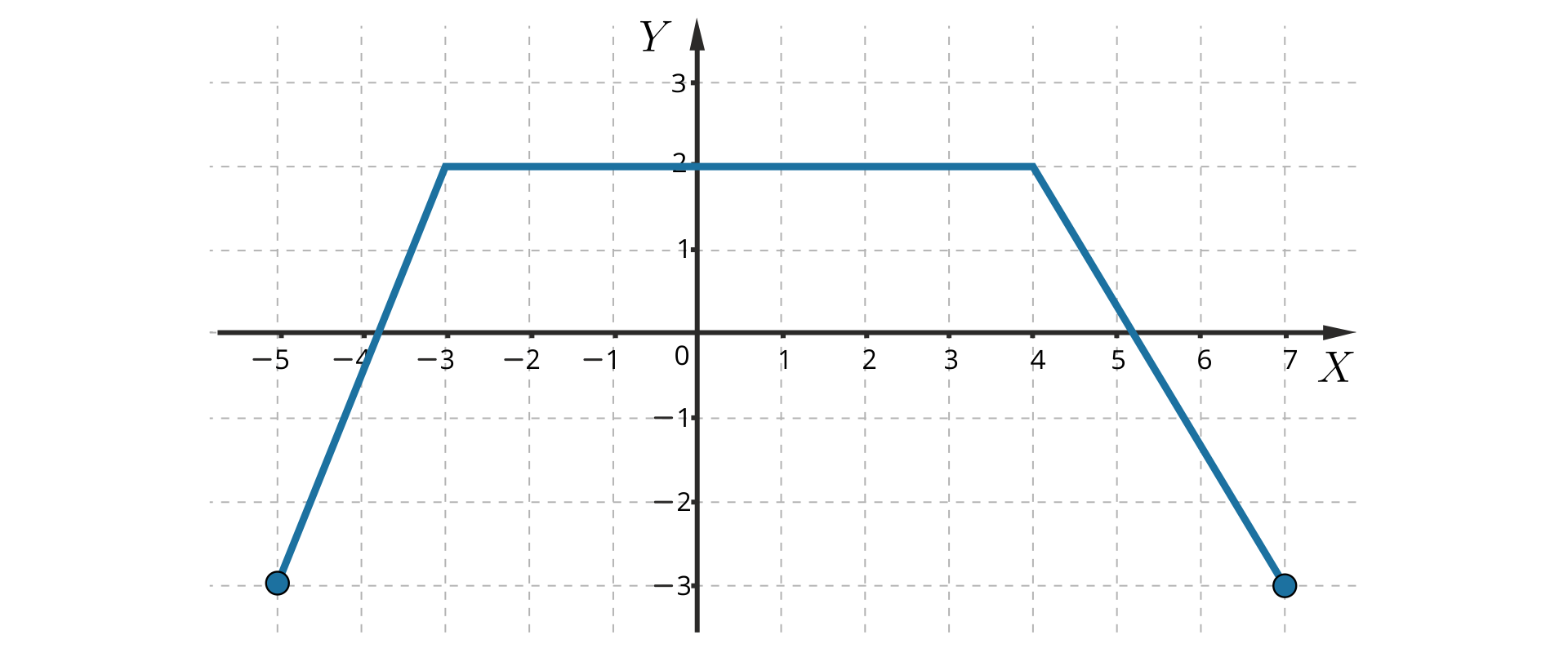
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R4guSFSxqD9QB
Uzupełnij luki w zdaniach, wpisując odpowiednie liczby. Maksymalnym przedziałem, w którym funkcja jest niemalejąca jest ⟨Tu uzupełnij,Tu uzupełnij⟩.Maksymalnym przedziałem, w którym funkcja jest nierosnąca jest ⟨Tu uzupełnij,Tu uzupełnij⟩.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Polecenie 1

Zapoznaj się z poniższym apletem i wykonaj zawarte w nim polecenia.

R1eveH7AB8ACo1

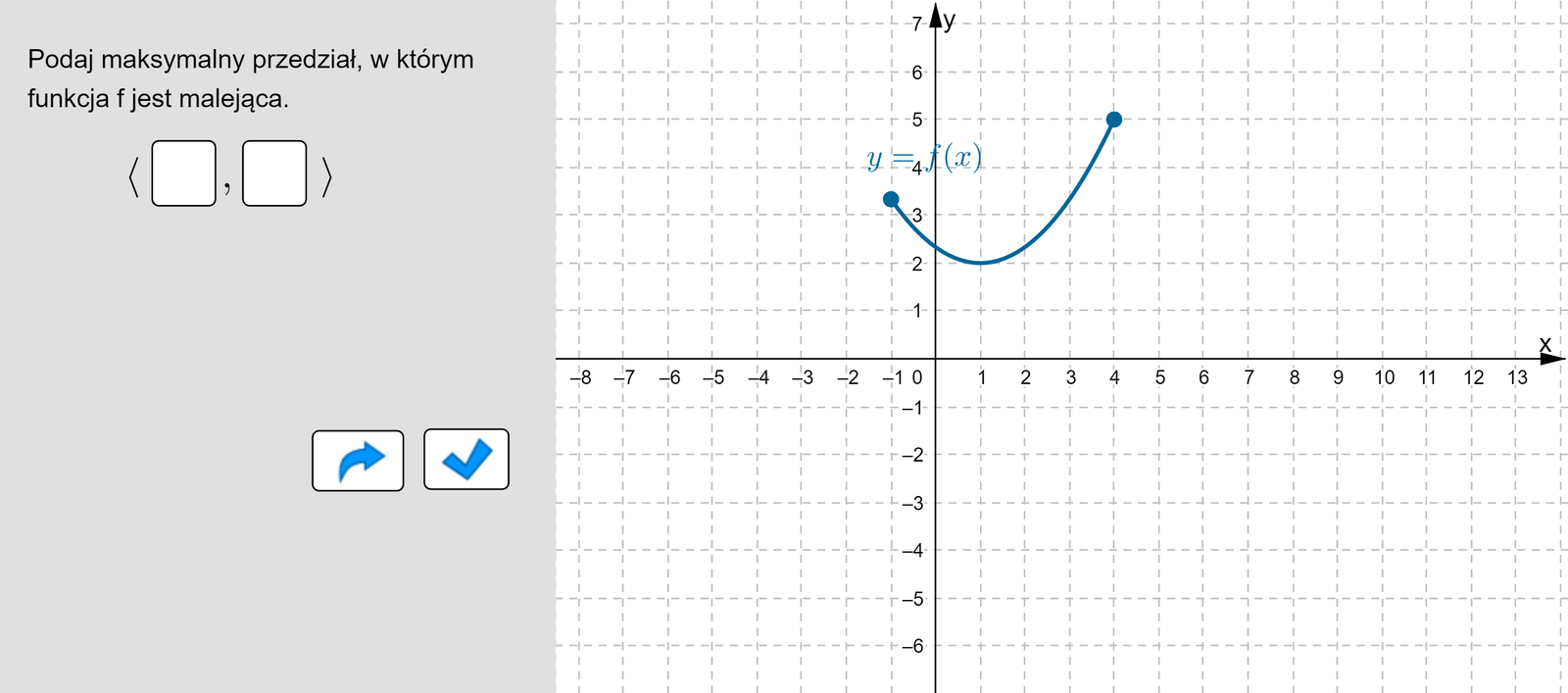
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PrBaJGP64

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rrsrox5Agl4yH
Uzupełnij poniższe zdania odpowiednimi przedziałami. Kliknij w lukę, aby rozwinąć listę i wybierz prawidłową odpowiedź. Wykresem pewnej funkcji jest parabola o początku w punkcie -1,-1 i końcu w punkcie 3,-1, której wierzchołkiem jest punkt 1,3.
Maksymalnym przedziałem, w którym ta funkcja jest rosnąca jest 1. ⟨3,4⟩, 2. ⟨-1,1⟩, 3. ⟨-3,112⟩, 4. ⟨4,5⟩, 5. ⟨1,3⟩, 6. ⟨112,6⟩.Wykresem pewnej funkcji jest parabola o początku w punkcie -3,0 i końcu w punkcie 6,0, której wierzchołkiem jest punkt 112,-5.
Maksymalnym przedziałem, w którym ta funkcja jest rosnąca jest 1. ⟨3,4⟩, 2. ⟨-1,1⟩, 3. ⟨-3,112⟩, 4. ⟨4,5⟩, 5. ⟨1,3⟩, 6. ⟨112,6⟩.Wykresem pewnej funkcji jest parabola o początku w punkcie 3,4 i końcu w punkcie 5,4, której wierzchołkiem jest punkt 4,3.
Maksymalnym przedziałem, w którym ta funkcja jest malejąca jest 1. ⟨3,4⟩, 2. ⟨-1,1⟩, 3. ⟨-3,112⟩, 4. ⟨4,5⟩, 5. ⟨1,3⟩, 6. ⟨112,6⟩.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.