Określenie liczebności zbiorów liczbowych skończonych
W tym materiale będziemy odpowiadać na pytania dotyczące liczebności zbiorów różnych rodzajów liczb. Trzeba będzie przy tym pamiętać, aby nie liczyć dwukrotnie tej samej liczby.
Aby lepiej zrozumieć problem, zapoznaj się z poniższą anegdotą.
André Ampére, francuski fizyk i matematyk (–), miał dwa koty – dużego i małego – które bardzo lubił. Przeszkadzały mu jednak ciągłym drapaniem do drzwi, więc w końcu kazał zrobić w drzwiach dwa otwory dla kotów – jeden duży – dla dużego, drugi mały – dla mniejszego, żeby mogły wchodzić i wychodzić same.
Jaki stąd wniosek? Duży kot i mały kot to po prostu kot. Podobnie z naszymi liczbami – jeśli ktoś poprosi nas o wypisanie wszystkich liczb naturalnych mniejszych od pięciu, to możemy zapisać liczby tak:
Albo na przykład tak:
, , , , , , , , .
I w pierwszym i w drugim przypadku jest tylko pięć liczb naturalnych mniejszych od pięciu.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
MultimediumMultimedium
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Określisz ile liczb jest w danym zbiorze.
Wykorzystasz cechy podzielności liczb w zadaniach.
Ustalisz liczbę elementów zbioru skończonegozbioru skończonego.
W matematyce często używanym pojęciem jest zbiór. Zbiór może składać się z figur geometrycznych (np. zbiór trójkątów), liczb (np. zbiór liczb naturalnych), przedmiotów (np. zbiór narzędzi ogrodniczych), a nawet ludzi (np. zbiór uczniów szkoły podstawowej).
Trójkąty, liczby, narzędzia ogrodnicze, czy osoby należące do danego zbioru to elementy tego zbioru. Dany element może należeć do zbioru lub nie. Na przykład do zbioru kwadratów nie należy okrąg.
Zbiór może mieć nieskończenie wiele elementów (np. zbiór liczb naturalnych parzystych) lub być zbiorem skończonymzbiorem skończonym. Czyli mieć określoną liczbę elementów (np. dziesięć).
Zbiory najczęściej oznaczamy dużymi literami, np. , , , . Np. elementami zbioru są: .
Oznaczmy przez zbiór reszt z dzielenia liczb naturalnych dodatnich przez .
Reszty te mogą być równe: , , , , . Są to elementy zbioru . Zapisujemy:
Zbiór ten ma elementów.
Kolejność zapisu elementów zbioru nie ma znaczenia, ale elementy nie mogą się powtarzać. Np.
Jeśli zbiór ma dużo elementów, to nie zawsze musimy je wszystkie wypisać. Jeżeli nie budzi to wątpliwości, możemy zastosować skrócony zapis z pomocą wielokropka.
Zbiór kolejnych liczb naturalnych mniejszych od możemy zapisać w postaci:
Często jest potrzeba ustalania z ilu elementów składa się dany zbiór (czyli określenia jego liczebności). Pokażemy teraz kilka przykładów wyznaczania liczebności zbiorów. Ograniczymy się tylko do zbiorów liczbowych.
Ustalimy, ile jest ułamków właściwych o mianowniku .
Ułamek właściwy, to ułamek, którego licznik jest mniejszy od mianownika. Wypiszemy wszystkie ułamki spełniające warunki zadania i policzymy ile ich jest.
Jest ułamków właściwych o mianowniku .
Możemy powiedzieć, że zbiór ułamków właściwych o mianowniku składa się z elementów.
Określimy, ile jest liczb całkowitych, które są większe od , ale mniejsze od .
Aby obliczyć ile jest takich liczb, zaznaczymy je na osi liczbowej, wypiszemy i policzymy.
Jest liczb spełniających warunki zadania.
Zbiór liczb całkowitych większych od , ale mniejszych od składa się z elementów.
Obliczymy, ile jest liczb naturalnych dwucyfrowych.
Oznaczmy przez zbiór liczb naturalnych dwucyfrowych.
Najmniejsza z liczb dwucyfrowych to , a największa to .
Wypiszemy wszystkie liczby naturalne dodatnie jednocyfrowe i dwucyfrowe:
Wśród tych liczb dziewięć to liczby jednocyfrowe. Zatem .
Czyli liczb naturalnych dwucyfrowych jest .
W zbiorze kolejnych liczb naturalnych jest elementów.
W zbiorze kolejnych liczb naturalnych jest elementów.
Ustalimy liczebność zbioru .
Skorzystamy z podanego wyżej wzoru.
Liczebność podanego zbioru jest równa .
Ustalimy, ile jest liczb naturalnych dwucyfrowych podzielnych przez .
Najmniejsza liczba dwucyfrowa podzielna przez to . Największa to .
Aby wyznaczyć, ile jest wszystkich takich liczb, niestety nie możemy skorzystać ze wzoru takiego, jak w poprzednim przykładzie. Bowiem kolejne liczby podzielne przez , to nie są kolejne liczby naturalne.
Zauważmy jednak, że kolejny element w zbiorze liczb dwucyfrowych podzielnych przez jest większy od poprzedniego o .
Wynika z tego, że co trzecia liczba dwucyfrowa jest podzielna przez . Z przykładu wiemy, że liczb dwucyfrowych jest .
Zatem, ponieważ jest dzielnikiem liczby . Liczb dwucyfrowych podzielnych przez jest więc .
Ustalimy, ile liczb trzycyfrowych o różnych cyfrach można utworzyć z cyfr , , .
Wypiszemy wszystkie takie liczby pamiętając, że cyfrą setek nie może być :
Z cyfr , , można utworzyć cztery liczby trzycyfrowe o różnych cyfrach.
Zbiór liczb trzycyfrowych o różnych cyfrach utworzonych z cyfr , , składa się z elementów.
Określimy liczbę elementów zbioru zawierającego liczby naturalne pierwsze mniejsze od .
Liczby naturalne mniejsze od to i . Żadna z tych liczb nie jest liczbą pierwszą. W zbiorze zawierającym liczby naturalne pierwsze mniejsze od nie ma żadnego elementu. O takim zbiorze mówimy, że jest zbiorem pustymzbiorem pustym.
Zbiór niezawierający żadnych elementów to zbiór pusty.
Notatki
Prezentacja multimedialna
Zapoznaj się z prezentacją. Rozwiąż najpierw samodzielnie zamieszczone tam zadania i dopiero wtedy porównaj z proponowanymi rozwiązaniami.
Film dostępny pod adresem /preview/resource/RHtSRi2D6vVyb
Film nawiązujący do treści materiału
Slajd pierwszy.
Lektor czyta: Zapoznaj się z przykładami ustalania liczebności zbiorów liczbowych. Na slajdzie pojawia się kadr w którym uczeń pisze wzory matematyczne na tablicy.
Slajd drugi.
Przykład pierwszy.
Ile jest liczb naturalnych mniejszych od czterdziestu, które w dzieleniu przez siedem dają resztę trzy?
Ustalimy, ile jest liczb naturalnych mniejszych od czterdziestu, które w dzieleniu przez siedem dają resztę trzy. Istotnie, . Najmniejsza z takich liczb to trzy, następna liczba to dziesięć, kolejna to siedemnaście. Zauważmy, że kolejne liczby różnią się o siedem. Zatem mamy, .
Odpowiedź: jest sześć liczb naturalnych mniejszych od czterdzieści, które w dzieleniu przez siedem dają resztę trzy.
Slajd trzeci.
Przykład drugi.
Ile jest liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste? Obliczymy, ile jest liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste.
Pierwszy sposób. Cyfry liczby naturalnej dwucyfrowej, w której obie cyfry są parzyste, wybieramy spośród cyfr zero, dwa, cztery, sześć, osiem. Wypisujemy wszystkie takie liczby i liczymy, że jest ich dwadzieścia. O to one: . Na slajdzie podane liczby zapisano w pięciu kolumnach i czterech wierszach.
Slajd czwarty.
Drugi sposób. Zauważmy, że cyfrę dziesiątek liczby, której obie cyfry są parzyste, możemy wybrać spośród cyfr: dwa, cztery, sześć, osiem. Są więc cztery możliwości wyboru takiej cyfry. Cyfrę jedności możemy natomiast wybrać spośród cyfr: zero, dwa, cztery, sześć, osiem. Jest więc pięć możliwości wyboru takiej cyfry. Wszystkich możliwości jest więc cztery razy pięć, czyli dwadzieścia.
Odpowiedź: jest dwadzieścia liczb dwucyfrowych, których obie cyfry są parzyste.
Slajd piąty.
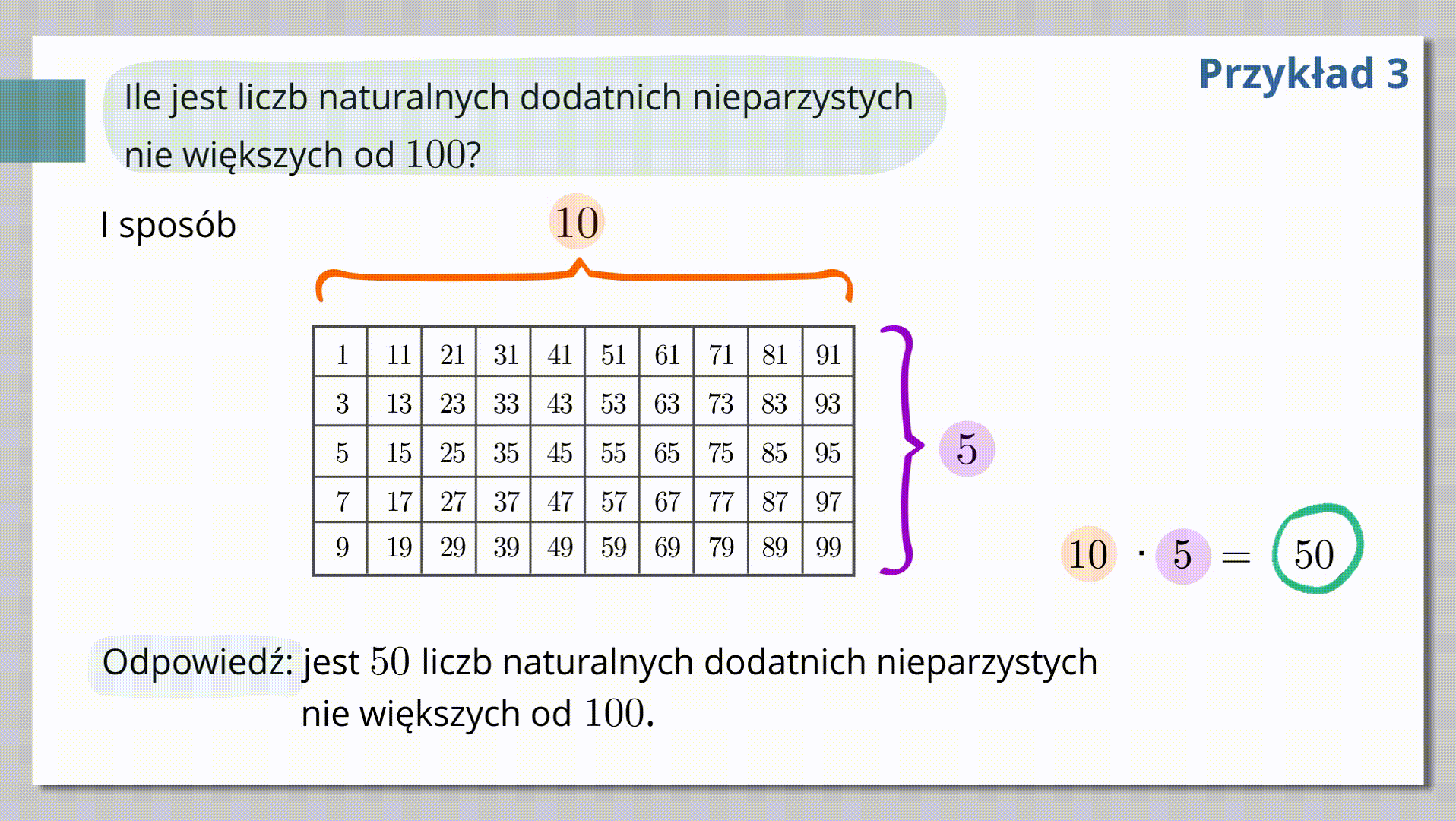
Przykład trzeci.
Ile jest liczb naturalnych dodatnich nieparzystych nie większych od stu?
Pierwszy sposób: Wypisujemy wszystkie takie liczby, czyli i obliczamy, że jest ich pięćdziesiąt. Na slajdzie wypisano wszystkie liczby nieparzyste mniejsze od stu w dziesięciu kolumnach i pięciu wierszach. Obok zapisano dziesięć razy pięć równa się pięćdziesiąt.
Slajd szósty.
Drugi sposób: Jest sto liczb naturalnych dodatnich nie większych od stu. Połowa z nich to liczby nieparzyste. Zatem , więc liczb nieparzystych nie większych od stu jest pięćdziesiąt.
Odpowiedź: jest pięćdziesiąt liczb naturalnych dodatnich nieparzystych nie większych od stu.
Slajd siódmy.
Przykład czwarty.
Ile jest liczb naturalnych parzystych, które są większe od sześćdziesięciu i zarazem mniejsze od dwustu czterdziestu sześciu? Tym razem liczb spełniających warunki zadania jest dużo. Nie ma więc sensu ich wszystkich wypisywać. Istotnie, . Podzielmy każdą z tych liczb przez dwa. Utwórzmy zbiór B, którego elementami będą otrzymane liczby. . Zauważmy, że w zbiorze A jest tyle samo elementów, co w zbiorze B. Elementy zbioru B to kolejne liczby naturalne od trzydziestu jeden do stu dwudziestu dwóch. Możemy więc skorzystać ze wzoru podanego w zakładce Ważne, czyli .
Odpowiedź: są dziewięćdziesiąt dwie liczby naturalne parzyste, które są większe od sześćdziesięciu i zarazem mniejsze od dwustu czterdziestu sześciu.
Slajd ósmy.
Przykład piąty.
Ustalimy, ile jest liczb naturalnych trzycyfrowych podzielnych przez trzy.
Pierwszy sposób: Najmniejsza z takich liczb to sto dwa, a największa to dziewięćset dziewięćdziesiąt dziewięć. Aby obliczyć ile tych liczb jest, skorzystamy ze sposobu podanego w poprzednim przykładzie, czyli .
Slajd dziewiąty.
Drugi sposób: Liczb naturalnych trzycyfrowych jest dziewięćset. Co trzecia jest podzielna przez trzy. Zatem jest trzysta liczb naturalnych trzycyfrowych podzielnych przez trzy, ponieważ .
Odpowiedź: jest trzysta liczb naturalnych trzycyfrowych podzielnych przez trzy.
Slajd dziesiąty.
Przykład szósty.
Obliczymy, ile jest liczb naturalnych pięciocyfrowych, których suma cyfr jest równa dwa. Zauważmy, że cyfra takiej liczby może być tylko równa dwa, jeden lub zero.
Dla dwójki mamy tylko jedną liczbę spełniającą warunki zadania. Jest to dwadzieścia tysięcy. Cyframi następnych liczb mogą być tylko dwie jedynki i trzy zera. Wypisujemy te liczby, pamiętając, że cyfrą dziesiątek tysięcy nie może być zero. Są to liczby . W sumie otrzymaliśmy pięć liczb pięciocyfrowych, których suma cyfr jest równa dwa.
Odpowiedź: jest pięć liczb naturalnych pięciocyfrowych, których suma cyfr jest równa dwa.
Slajd jedenasty.
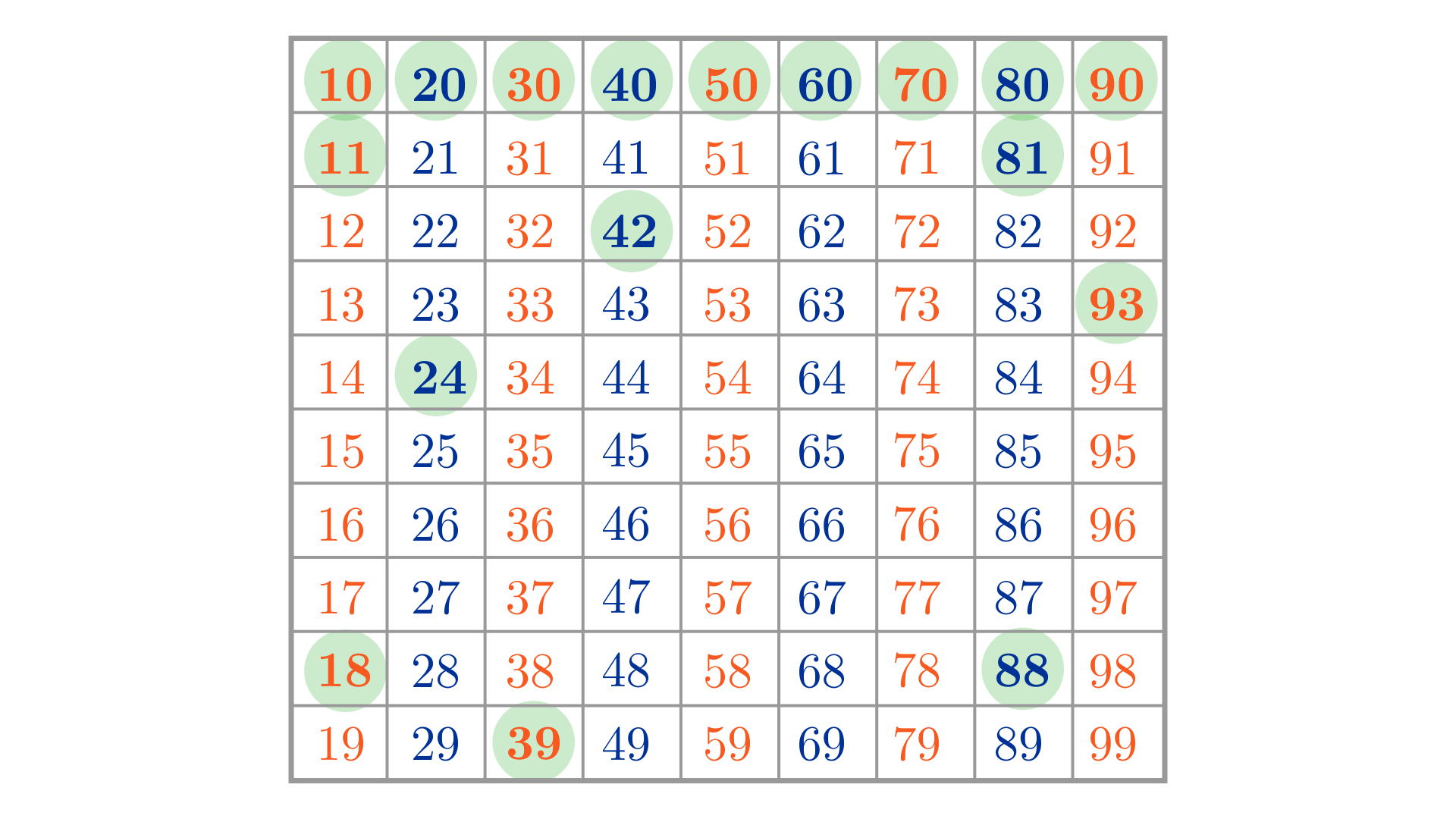
Przykład siódmy.
Ile jest różnych liczb naturalnych dwucyfrowych, których suma cyfr jest kwadratem liczby naturalnej dodatniej? Pierwszy sposób. Wypisujemy wszystkie liczby dwucyfrowe. Cyfry na slajdzie zostały zapisane w dziesięciu wierszach i dziesięciu kolumnach. Zaznaczamy te, których suma cyfr jest kwadratem liczby naturalnej. Są to liczby . Obliczamy, że jest siedemnaście takich liczb.
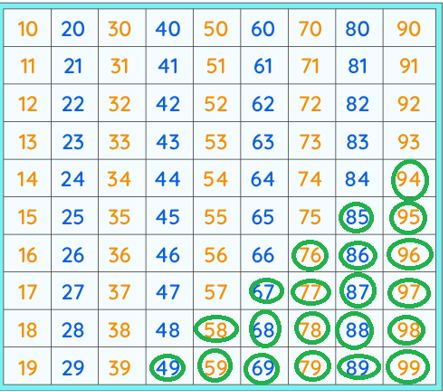
Slajd dwunasty.
Zauważmy, że największa liczba dwucyfrowa to dziewięćdziesiąt dziewięć. Jej suma cyfr to osiemnaście. Będziemy więc rozważać tylko liczby mniejsze od osiemnastu, będące kwadratami liczb naturalnych dodatnich. Są tylko cztery takie liczby. Są to liczby , ponieważ są to odpowiednio . Liczbę jeden można zapisać tylko jednym sposobem w postaci sumy. Czyli jest tylko jedna liczba dwucyfrowa, której suma cyfr jest równa jeden. Liczbę cztery można zapisać na cztery sposoby w postaci sumy. Istotni, , , oraz . Zatem są cztery liczby naturalne dwucyfrowe, których suma cyfr jest równa cztery. Liczbę dziewięć można zapisać aż na dziewięć sposobów w postaci sumy. Istotnie, , , , , , , , oraz . Zatem jest dziewięć liczb naturalnych dwucyfrowych, których suma cyfr jest równa dziewięć.
Liczbę szesnaście można zapisać na trzy sposoby w postaci sumy. Istotnie, , oraz . Zatem są trzy liczby naturalne dwucyfrowe, których suma cyfr jest równa szesnaście. Obliczamy, że wszystkich otrzymanych liczb jest siedemnaście. Są to liczby .
Odpowiedź: wszystkich liczb naturalnych dwucyfrowych, których suma cyfr jest kwadratem liczby naturalnej dodatniej jest siedemnaście.
Koniec prezentacji.
Ile różnych liczb naturalnych trzycyfrowych podzielnych przez można utworzyć z cyfr , , ?
Ile jest różnych liczb naturalnych czterocyfrowych, których suma cyfr jest równa ?
Ile jest liczb naturalnych dwucyfrowych, których iloczyn cyfr jest sześcianem liczby naturalnej?
Zestaw ćwiczeń interaktywnych
Zapisz ile liczb naturalnych trzycyfrowych podzielnych przez można utworzyć z cyfr , , ?
Zapisz ile jest liczb naturalnych dwucyfrowych, których suma cyfr jest większa od ?
Słownik
zbiór składający się z określonej liczby elementów.
zbiór niezawierający żadnych elementów.
Bibliografia
Conway John H., Guy Richard K., (1999), Księga liczb, Warszawa: Wydawnictwo Naukowo - Techniczne,