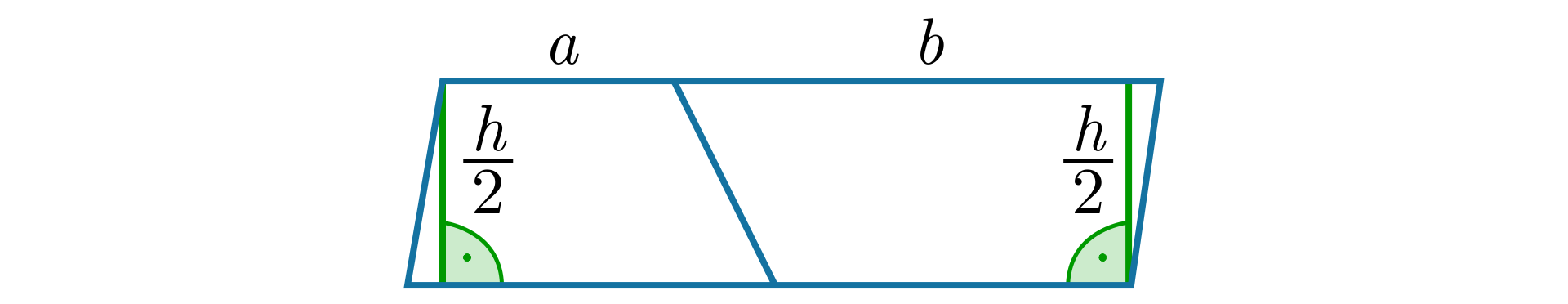Pole trapezu
Trapez to czworokąt mający co najmniej jedną parę boków równoległych. Zatem trapezami są np. równoległoboki. Prostokąt to szczególny przykład trapezu prostokątnego, czyli takiego, w którym jest kąt prosty. Trapez równoramienny to trapez, w którym ramiona są równe i nierównoległe.
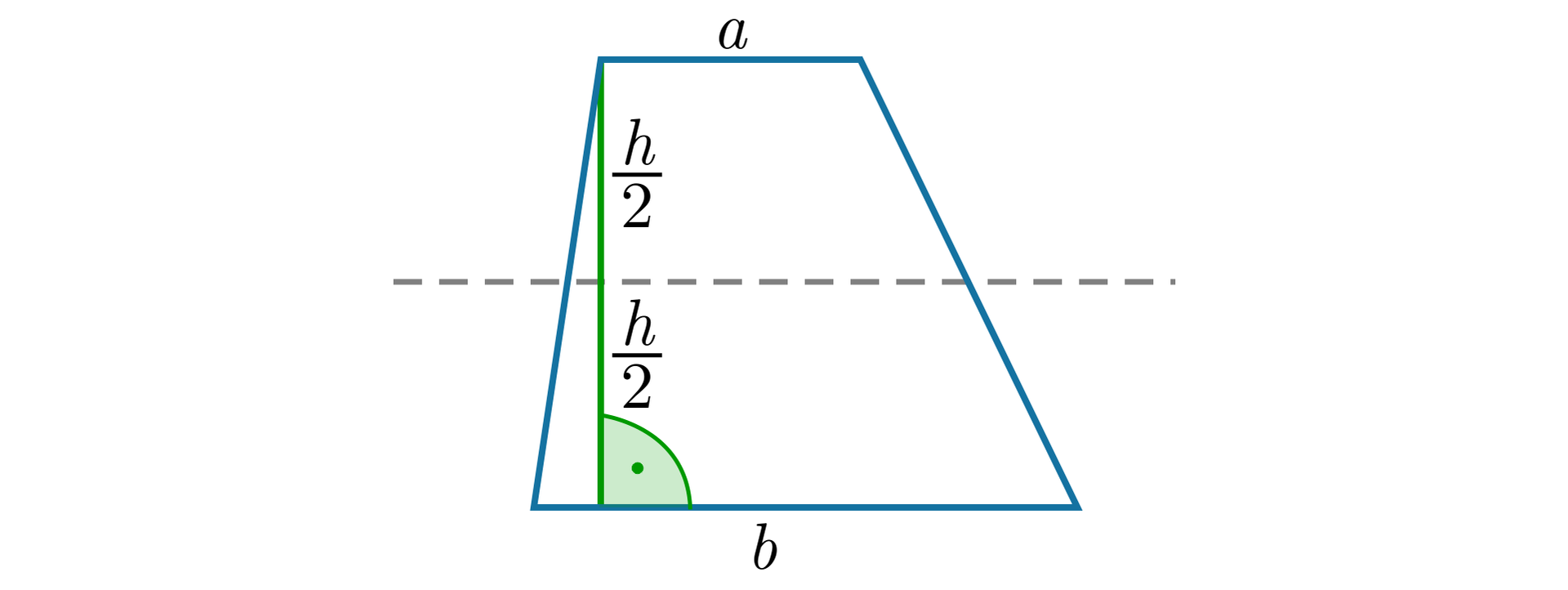
Wysokością w trapezie jest odległość między podstawami.

Znajdź obraz trapezu w symetrii względem środka boku .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P5ncxCvLB
Otrzymany trapez jest przystający do trapezu .
Jeśli podstawy trapezu mają długości i , natomiast odległość między nimi jest równa , to jakie jest pole otrzymanego równoległoboku?
Pole trapezu o podstawach długości oraz i wysokości jest równe

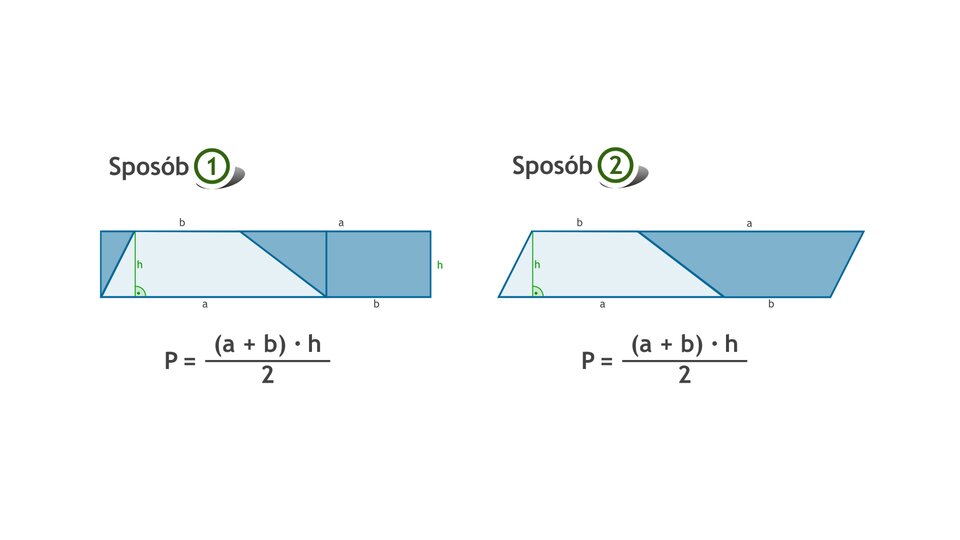
Film dostępny pod adresem /preview/resource/RbbpLlewCXnlo
Animacja przedstawia i uzasadnia prawdziwość wzoru na pole trapezu.
Obliczanie pola trapezu
W trapezie równoramiennym wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na odcinki: długości i długości . Ramię jest równe krótszej podstawie. Oblicz pole trapezu.

Trapez jest równoramienny, zatem . Wynika z tego, że
.
Długość ramienia jest równa krótszej podstawie, czyli wynosi .
Wysokość trapezu obliczamy z trójkąta prostokątnego , stosując twierdzenie Pitagorasa.
Obliczamy pole trapezu.
Pole trapezu jest równe .
Podstawy trapezu prostokątnego są równe i . Pole trapezu jest równe . Oblicz obwód trapezu.

Obliczamy wysokość trapezu , korzystając ze wzoru na pole trapezu.
Trójkąt jest prostokątny. Obliczmy długość jego przeciwprostokątnej na podstawie twierdzenia Pitagorasa.
Zauważmy, że długość ramienia jest równa wysokości. Obliczamy obwód trapezu.
Obwód trapezu jest równy .
Piaskownica ma kształt sześciokąta o wymiarach (w ) podanych na rysunku. Oblicz w pole powierzchni zajmowane przez piaskownicę.

Zauważmy, że sześciokąt, w kształcie którego jest piaskownica, możemy podzielić na dwa przystające trapezy o podstawach długości i oraz wysokości . Pole powierzchni piaskownicy jest więc równe sumie pól tych trapezów.
Zapisujemy pole powierzchni piaskownicy w , pamiętając, że .
Pole powierzchni piaskownicy jest równe .
Oblicz pole każdej z figur, przyjmując za jednostkę pole jednej kratki.

Wykaż, że pola wielokątów , , są równe.

Wysokość trapezu jest równa . Oblicz pole trapezu, wiedząc, że
suma długości jego podstaw jest równa ;
jedna z podstaw trapezu jest trzykrotnie dłuższa od drugiej, a krótsza podstawa ma długość ;
jego przekątne są równe i przecinają się w połowie pod kątem prostym;
jest to trapez prostokątny i kąt ostry ma miarę , a krótsza podstawa ma długość .
Oblicz pole każdego z trapezów: , , .

Odpowiedź: Wysokość tego trapezu wynosi Tu uzupełnij. Ile wynosi długość jednej z podstaw, jeżeli długość drugiej jest równa , a wysokość wynosi ?
Odpowiedź: Długość tej podstawy wynosi Tu uzupełnij.
Ile arów powierzchni ma działka pani Bożeny w kształcie trapezu przedstawionego na rysunku? Wymiary podane są w metrach.

- Wysokość trapezu może być jego bokiem.
- Dwa trapezy mające podstawy tej samej długości mają równe pola.
- Dwa trapezy równoramienne mające wysokości oraz ramiona tej samej długości mają równe pola.
- Trapezy przystające mają równe pola.
Udowodnij, że każdy trapez możemy przebudować na prostokąt o wymiarach na , gdzie to długość krótszej podstawy trapezu, to długość dłuższej podstawy trapezu, a to jego wysokość.
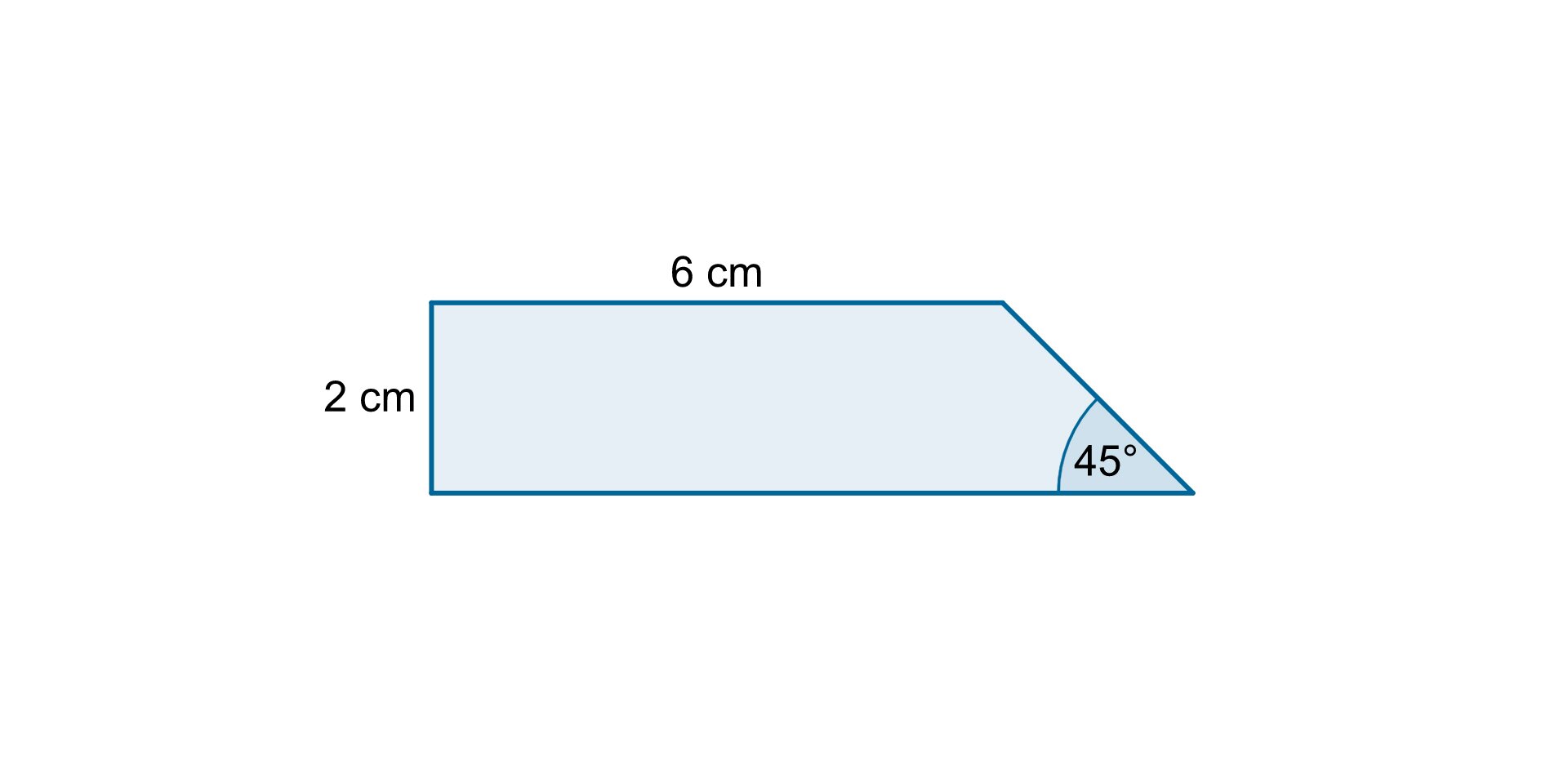
Oblicz, ile wynosi pole trapezu przedstawionego na poniższym rysunku.
Wykaż, że pole trapezu jest równe polu trójkąta .

Dokończ zdanie, wybierając poprawne odpowiedzi.
Czworokątem tym może być Możliwe odpowiedzi: 1. trapez, 2. kwadrat, 3. równoległobok
- trapez
- kwadrat
- równoległobok
Obraz w kształcie prostokąta ma wymiary i . Drzwi w kształcie prostokąta mają wymiary i . Czy obraz można przenieść przez drzwi?