Powtórzenie wiadomości o figurach płaskich

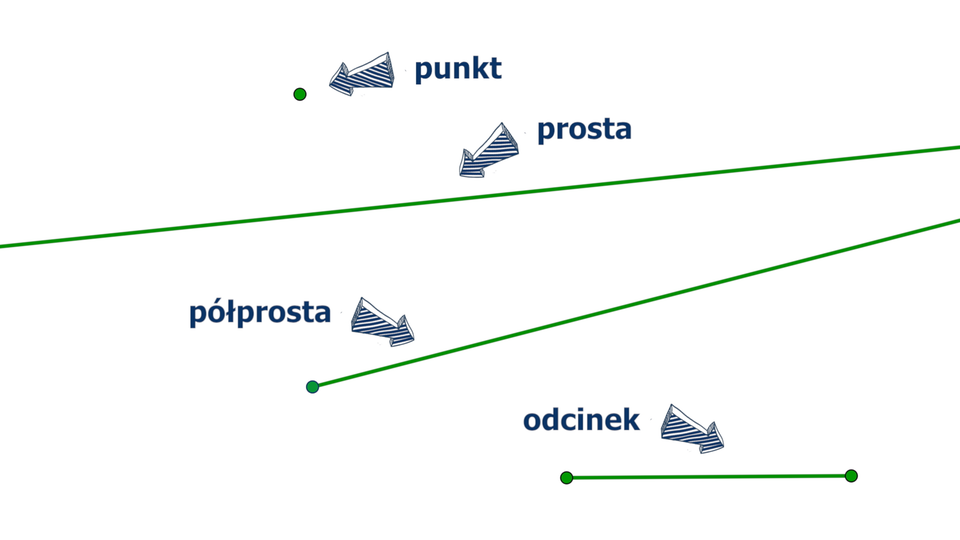
Punkt, odcinek, półprosta, prosta

R12TqyRrx6ciL1
Animacja przedstawia kilka podstawowych figur geometrycznych.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R12TqyRrx6ciL

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia kilka podstawowych figur geometrycznych.

11
Ćwiczenie 1
RV8nLmnAgh20t11
Połącz w pary rysunek z jego opisem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Delnk4Adaxz
Połącz w pary definicje z nazwami obiektów, które definiują. Obiekt, który składa się z nieskończenie wielu punktów ułożonych wzdłuż jednej linii. Możliwe odpowiedzi: 1. Proste równoległe, 2. Odcinek, 3. Proste prostopadłe, 4. Półprosta, 5. Prosta Obiekt, który jest częścią prostej ograniczonej z jednej strony przez punkt. Możliwe odpowiedzi: 1. Proste równoległe, 2. Odcinek, 3. Proste prostopadłe, 4. Półprosta, 5. Prosta Obiekt, który jest częścią prostej zawartej pomiędzy dwoma punktami tej prostej, z tymi punktami włącznie. Możliwe odpowiedzi: 1. Proste równoległe, 2. Odcinek, 3. Proste prostopadłe, 4. Półprosta, 5. Prosta Dwie proste, które nie mają żadnych punktów wspólnych. Możliwe odpowiedzi: 1. Proste równoległe, 2. Odcinek, 3. Proste prostopadłe, 4. Półprosta, 5. Prosta Dwie proste, które przecinają się pod kątem 90°. Możliwe odpowiedzi: 1. Proste równoległe, 2. Odcinek, 3. Proste prostopadłe, 4. Półprosta, 5. Prosta
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 2

Narysuj

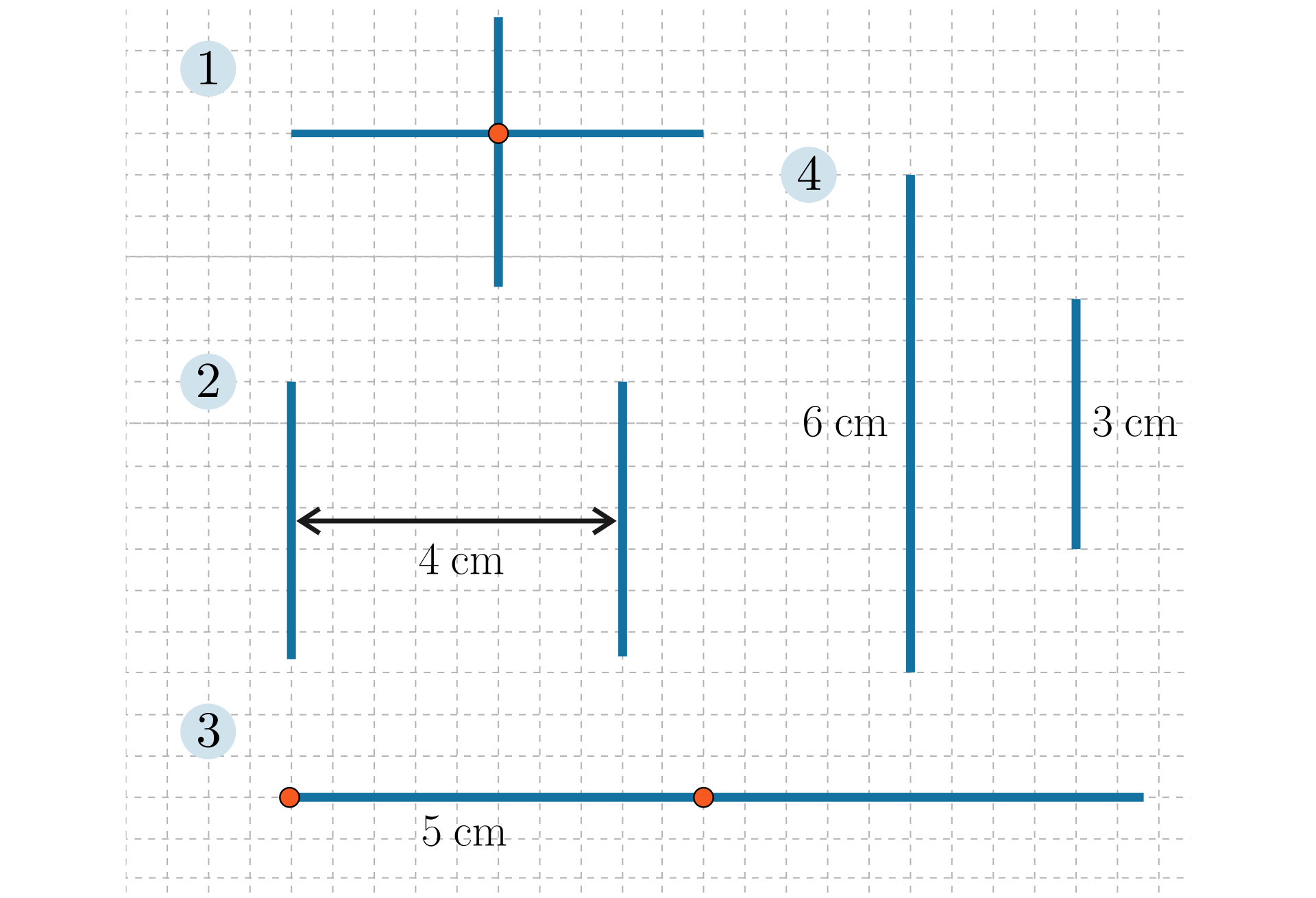
  1. punkt oraz dwie proste prostopadłe przecinające się w tym punkcie.

  2. dwie proste równoległe, oddalone od siebie o 4 centymetry.

  3. półprostą i punkt leżący na półprostej i oddalony od jej początku o 5 cm.

  4. dwa odcinki równoległe o długościach 6 cm i 3 cm.

Przyjmij, że dwie kratki oznaczają odległość 1 cm.

RFRFk8InoFKaF
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Opisz etapy rysowania

  1. punktu oraz dwóch prostych prostopadłych przecinających się w tym punkcie.

  2. dwóch prostych równoległych, oddalonych od siebie o 4 centymetry.

  3. półprostej i punktu leżącego na półprostej i oddalonego od jej początku o 5 cm.

  4. dwóch odcinków równoległych o długościach 6 cm i 3 cm.

Rxp8q2ilpwzfD11
Ćwiczenie 3
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Dwie proste, które nie są równoległe zawsze przecinają się w jednym punkcie., 2. Przez dwa punkty może przejść tylko jedna prosta., 3. Dwa nierównoległe odcinki muszą się przecinać., 4. Dwa odcinki prostopadłe nie muszą się przecinać.

  • Dwie proste, które nie są równoległe zawsze przecinają się w jednym punkcie.
  • Przez dwa punkty może przejść tylko jedna prosta.
  • Dwa nierównoległe odcinki muszą się przecinać.
  • Dwa odcinki prostopadłe nie muszą się przecinać.
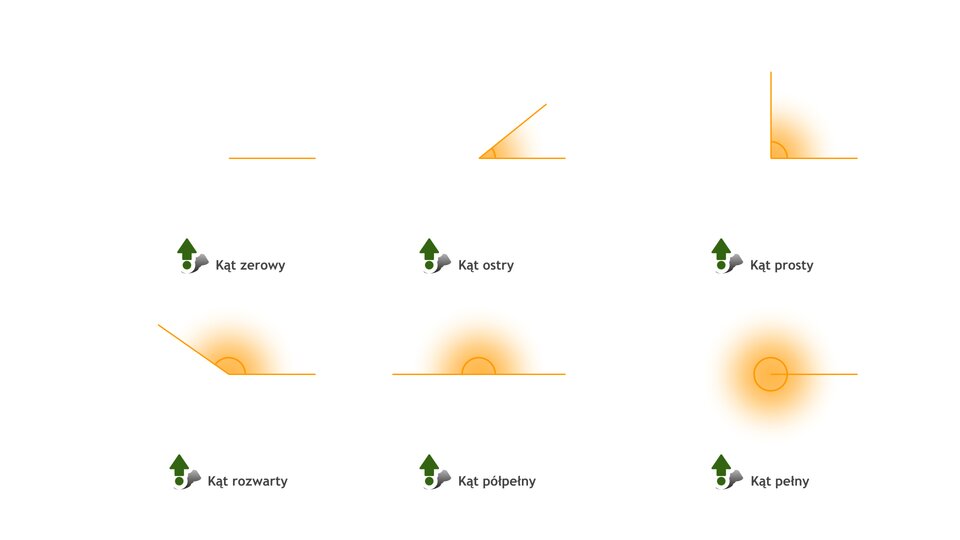
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Kąty

Kąt
Definicja: Kąt

Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.

Już wiesz
RgUUvB8Q3oSoj1
Animacja przedstawia wszystkie możliwe rodzaje kątów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RgUUvB8Q3oSoj

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia wszystkie możliwe rodzaje kątów.

R9SVMSVzfRuHO11
Ćwiczenie 4
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Każdy kąt ma wierzchołek i dwa ramiona., 2. Kąt ostry ma więcej niż 90 ° ., 3. Kąt prosty ma 90 ° ., 4. Kąt rozwarty ma więcej niż 90 ° i mniej niż 180 ° ., 5. W kącie półpełnym ramiona kąta tworzą prostą., 6. Ramiona kąta nie należą do tego kąta.

  • Każdy kąt ma wierzchołek i dwa ramiona.
  • Kąt ostry ma więcej niż 90 ° .
  • Kąt prosty ma 90 ° .
  • Kąt rozwarty ma więcej niż 90 ° i mniej niż 180 ° .
  • W kącie półpełnym ramiona kąta tworzą prostą.
  • Ramiona kąta nie należą do tego kąta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 5

Dwie przecinające się proste utworzyły kąty α, β, γ i δ. Dana jest miara jednego z tych kątów. Oblicz miary trzech pozostałych kątów.

R1RaFOqghtBdS1
Rysunek dwóch przecinających się prostych, które utworzyły kąty alfa, beta, gamma i delta. Kąt alfa leży naprzeciwko kąta gamma, są to kąty rozwarte. Kąt beta leży naprzeciwko kąta delta, są to kąty ostre.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rwm4dC5WK2zb11
Uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. α=134°, β= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, γ= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, δ=1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°
β=28°, α= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, γ= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, 𝛿= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°
γ= 91°, α= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, β 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°, 𝛿= 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych°
Kąty α i δ, δ i γ, γ i β oraz β i α to pary kątów 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych.
Kąty α i γ oraz β i δ to pary kątów 1. 110, 2. 110, 3. 152, 4. 53, 5. 46, 6. przyległych, 7. 37, 8. 89, 9. 46, 10. 152, 11. 89, 12. 134, 13. 91, 14. 28, 15. 37, 16. 53, 17. wierzchołkowych.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąt, czworokąt i inne wielokąty

2
Ćwiczenie 6

Policz i wpisz w puste pola, ile jest na rysunku wielokątów danego rodzaju.

RX9uu80wIWlf51
Rysunki trzynastu figur: trójkątów, czworokątów, pięciokątów i sześciokątów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rk4GpKLrbRptH1
Na rysunku przedstawiono: Tu uzupełnij trójkąty, Tu uzupełnij trójkąty ostrokątne, Tu uzupełnij trójkąt prostokątny, Tu uzupełnij trójkąt rozwartokątne, Tu uzupełnij trapezów, Tu uzupełnij czworokątów, Tu uzupełnij równoległoboków, Tu uzupełnij prostokąty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RaPYkALca4dmP
Połącz w pary definicje z nazwami odpowiednich figur. Trójkąt, którego wszystkie kąty mają miarę mniejszą niż 90°. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez Trójkąt, którego jeden kąt ma miarę 90°. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez Trójkąt, którego jeden kąt ma miarę większą niż 90°. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez Czworokąt, który ma jedną parę boków równoległych. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez Czworokąt, który ma dwie pary boków równoległych. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez Czworokąt, który ma wszystkie kąty miary 90°. Możliwe odpowiedzi: 1. Prostokąt, 2. Trójkąt rozwartokątny, 3. Równoległobok, 4. Trójkąt ostrokątny, 5. Trójkąt prostokątny, 6. Trapez
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rsesvokmxsiob21
Ćwiczenie 7
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Przekątną wielokąta nazywamy 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa łączący 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa wierzchołki wielokąta, które nie leżą na 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa figury. Każda 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa dzieli wielokąt na 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa wielokąty, które mają w sumie o 1. dwa, 2. cztery, 3. cięciwa, 4. trójkąt, 5. odcinek, 6. dwa, 7. przekątna, 8. prostą, 9. trzy, 10. wewnątrz, 11. tym samym boku, 12. dwa kąty więcej niż dany wielokąt.

Wybierz.

dwa, przekątna, trzy, wewnątrz, odcinek, trójkąt, cztery, prostą, dwa, cięciwa, tym samym boku, dwa

Przekątną wielokąta nazywamy ............................ łączący ............................ wierzchołki wielokąta, które nie leżą na ............................ figury. Każda ............................ dzieli wielokąt na ............................ wielokąty, które mają w sumie o ............................ kąty więcej niż dany wielokąt.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1LKcpfS2nCPJ21
Ćwiczenie 8
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Każdy wielokąt ma tyle samo kątów, ile boków., 2. Żaden trójkąt nie ma przekątnych, 3. Kwadrat to prostokąt, który ma wszystkie boki tej samej długości., 4. Każdy wielokąt o liczbie boków większej od 3 ma więcej przekątnych niż boków., 5. Trapez prostokątny równoramienny nazywa się prostokątem.

  • Każdy wielokąt ma tyle samo kątów, ile boków.
  • Żaden trójkąt nie ma przekątnych
  • Kwadrat to prostokąt, który ma wszystkie boki tej samej długości.
  • Każdy wielokąt o liczbie boków większej od 3 ma więcej przekątnych niż boków.
  • Trapez prostokątny równoramienny nazywa się prostokątem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1T8ho1op0j8g21
Ćwiczenie 9
Który wielokąt opisujemy używając następujących słów? Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Używając słów: przyprostokątna i przeciwprostokątna opisujemy 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt.Używając słów: wierzchołek, bok i przekątna opisujemy 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt.Używając słów: ramię i podstawa opisujemy 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt oraz 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt.Używając słów: kąt przy wierzchołku opisujemy 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt.Używając słów: obwód i pole opisujemy 1. tylko trójkąt równoboczny, 2. tylko trójkąt prostokątny, 3. każdy wielokąt oprócz trójkąta, 4. każdy trójkąt, 5. trójkąt równoramienny, 6. trapez, 7. każdy wielokąt, 8. każdy wielokąt.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RbpQbpSfabNVM21
Ćwiczenie 10
Dobierz w pary stwierdzenie i jego uzasadnienie. Każdy wielokąt ma tyle samo kątów, ile boków. Możliwe odpowiedzi: 1. Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta., 2. Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste., 3. Przekątne kwadratu dzielą go na 4 trójkąty, w których dwa kąty mają po 45°, wobec tego trzeci kąt ma 90°., 4. Pięciokąt ma pięć przekątnych., 5. Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem. Żaden trójkąt nie ma przekątnych. Możliwe odpowiedzi: 1. Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta., 2. Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste., 3. Przekątne kwadratu dzielą go na 4 trójkąty, w których dwa kąty mają po 45°, wobec tego trzeci kąt ma 90°., 4. Pięciokąt ma pięć przekątnych., 5. Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem. Przekątne kwadratu przecinają się pod kątem prostym. Możliwe odpowiedzi: 1. Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta., 2. Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste., 3. Przekątne kwadratu dzielą go na 4 trójkąty, w których dwa kąty mają po 45°, wobec tego trzeci kąt ma 90°., 4. Pięciokąt ma pięć przekątnych., 5. Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem. Nie każdy wielokąt o liczbie boków większej od 4 ma więcej przekątnych niż boków. Możliwe odpowiedzi: 1. Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta., 2. Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste., 3. Przekątne kwadratu dzielą go na 4 trójkąty, w których dwa kąty mają po 45°, wobec tego trzeci kąt ma 90°., 4. Pięciokąt ma pięć przekątnych., 5. Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem. Trapez prostokątny równoramienny jest prostokątem. Możliwe odpowiedzi: 1. Ramiona każdego kąta wielokąta zawierają dwa boki wielokąta., 2. Trapez prostokątny równoramienny ma dwa boki tworzące z podstawami kąty proste., 3. Przekątne kwadratu dzielą go na 4 trójkąty, w których dwa kąty mają po 45°, wobec tego trzeci kąt ma 90°., 4. Pięciokąt ma pięć przekątnych., 5. Przekątna wielokąta to odcinek łączący dwa wierzchołki wielokąta i nie będący jego bokiem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

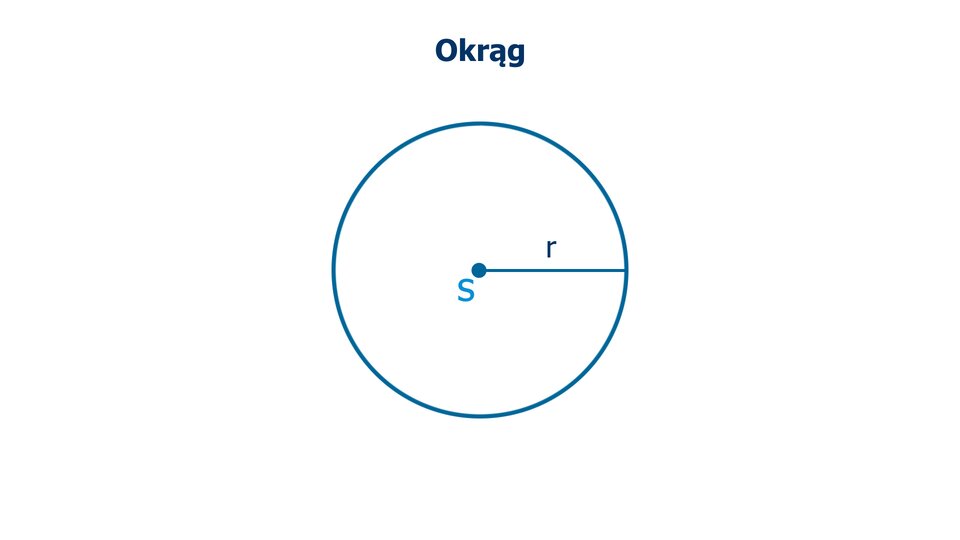
Koła i okręgi

Okrąg
Definicja: Okrąg

Okręgiem nazywamy figurę złożoną ze wszystkich punktów płaszczyzny równo oddalonych od ustalonego punktu, zwanego środkiem okręgu.

RoHyI0p2nnZj91
Animacja przedstawia jakie figury nazywamy okręgami.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RoHyI0p2nnZj9

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jakie figury nazywamy okręgami.

Koło
Definicja: Koło

Kołem o środku w punkcie S i promieniu r nazywamy figurę zbudowaną ze wszystkich punktów płaszczyzny, których odległość od punktu S jest mniejsza bądź równa promieniowi.

RaZfNDRwXSSzT1
Animacja przedstawia jakie figury nazywamy koła.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

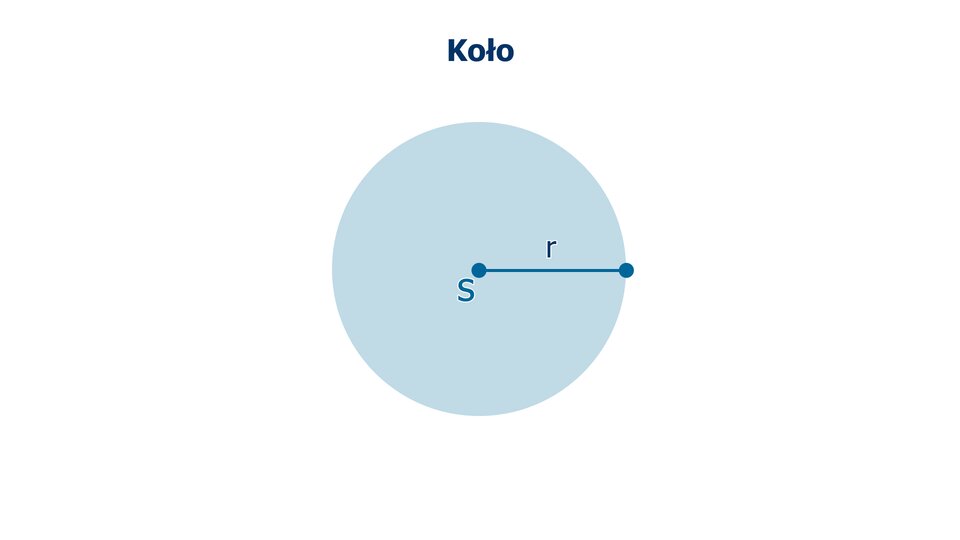
Film dostępny pod adresem /preview/resource/RaZfNDRwXSSzT

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jakie figury nazywamy koła.

3
Ćwiczenie 11

Zapoznaj się z poniższą ilustracją, przedstawiającą okrąg i koło.

R1W4vGivWtKIO1
Na rysunku znajdują się dwie figury. Figura A to okrąg o środku w punkcie A. Na tym okręgu zaznaczono punkt B. Figura B to koło o środku w punkcie A. Wewnątrz tego koła zaznaczono punkt B w taki sposób, że nie znajduje się on na brzegu tego koła.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12WFRCv3xENX1
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Rysunek figury A
Punkt B należy do 1. okręgu, 2. koła jest równa, 3. koła, 4. okręgu jest mniejsza, 5. kołą jest większa, 6. okręgu jest równa o środku w punkcie A.
Długość promienia tego 1. okręgu, 2. koła jest równa, 3. koła, 4. okręgu jest mniejsza, 5. kołą jest większa, 6. okręgu jest równa długości odcinka AB.
Rysunek figury B
Punkt B należy do 1. okręgu, 2. koła jest równa, 3. koła, 4. okręgu jest mniejsza, 5. kołą jest większa, 6. okręgu jest równa o środku w punkcie A.
Długość promienia tego 1. okręgu, 2. koła jest równa, 3. koła, 4. okręgu jest mniejsza, 5. kołą jest większa, 6. okręgu jest równa długości odcinka AB.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1O9eVLSS6ym431
Ćwiczenie 12
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odcinek, którego końcami są środek okręgu i dowolny punkt leżący na okręgu, to 1. średnicą, 2. krótsza, 3. dłuższa, 4. promień, 5. średnica, 6. promieniem, 7. cięciwa, 8. cięciwa, 9. promień.Odcinek, którego końce leżą na okręgu to 1. średnicą, 2. krótsza, 3. dłuższa, 4. promień, 5. średnica, 6. promieniem, 7. cięciwa, 8. cięciwa, 9. promień.Najdłuższą cięciwę koła lub okręgu nazywamy 1. średnicą, 2. krótsza, 3. dłuższa, 4. promień, 5. średnica, 6. promieniem, 7. cięciwa, 8. cięciwa, 9. promień.Średnica jest dwa razy 1. średnicą, 2. krótsza, 3. dłuższa, 4. promień, 5. średnica, 6. promieniem, 7. cięciwa, 8. cięciwa, 9. promień od promienia koła lub okręgu.

Wybierz.

promień, krótsza, promień, średnica, dłuższa, promieniem, średnicą, cięciwa, cięciwa

a) Odcinek, którego końcami są środek okręgu i dowolny punkt leżący na okręgu, to .....................
b) Odcinek, którego końce leżą na okręgu to .....................
c) Najdłuższą cięciwę koła lub okręgu nazywamy .....................
d) Średnica jest dwa razy .................... od promienia koła lub okręgu.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
31
Ćwiczenie 13
R1eieFuho46ba
Podano długości promieni: okręgu o środku w punkcie A i okręgu o środku w punkcie B. Jaką długość ma promień trzeciego okręgu? Uzupełnij poniższe tabele, przeciągając do jej komórek odpowiednie liczby.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RRHVFBxTibSnj
Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Dany jest okrąg A o promieniu 5 cm i okrąg B o promieniu 4 cm. Średnica okręgu A wynosi Tu uzupełnij cm, a średnica okręgu B wynosi Tu uzupełnij cm. Skonstruowano trzeci okrąg, którego średnica to suma średnic okręgów A i B. Promień trzeciego okręgu wynosi Tu uzupełnij cm. Dany jest okrąg A o promieniu 7 cm i okrąg B o promieniu 3 cm. Średnica okręgu A wynosi Tu uzupełnij cm, a średnica okręgu B wynosi Tu uzupełnij cm.Skonstruowano trzeci okrąg, którego średnica to różnica średnic okręgów A i B. Promień trzeciego okręgu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RHmrqqJ27Yest2
Ćwiczenie 14
Odpowiedz na pytania lub uzupełnij tekst. 1. Figura złożona z punktów równo oddalonych od środka tej figury., 2. Odcinki łączące przeciwległe wierzchołki figur., 3. Kąt o mierze większej niż 90° i mniejszej niż 180°, 4. Połowa średnicy okręgu., 5. Jest nim zarówno trójkąt, czworokąt jak i pięciokąt., 6. Czworokąt, który ma wszystkie boki tej samej długości i wszystkie kąty tej samej miary., 7. Linia, która nie ma ani początku, ani końca., 8. Fragment prostej, który ma początek i koniec., 9. Czworokąt, w którym co najmniej jedna para boków jest równoległa.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.