Prawdopodobieństwo zdarzenia losowego
Prawdopodobieństwem zdarzenia losowego () nazywamy stosunek liczby wyników sprzyjających temu zdarzeniu () do liczby wszystkich możliwych wyników () tego zdarzenia losowego.
W tym materiale omówimy sposoby obliczania prawdopodobieństwa zdarzeń podczas dwukrotnego rzutu kostką lub monetą oraz w innych sytuacjach z życia codziennego, a także zasady stosowania reguły mnożenia oraz reguły dodawania, również w sytuacjach wymagających rozważenia kilku przypadków.
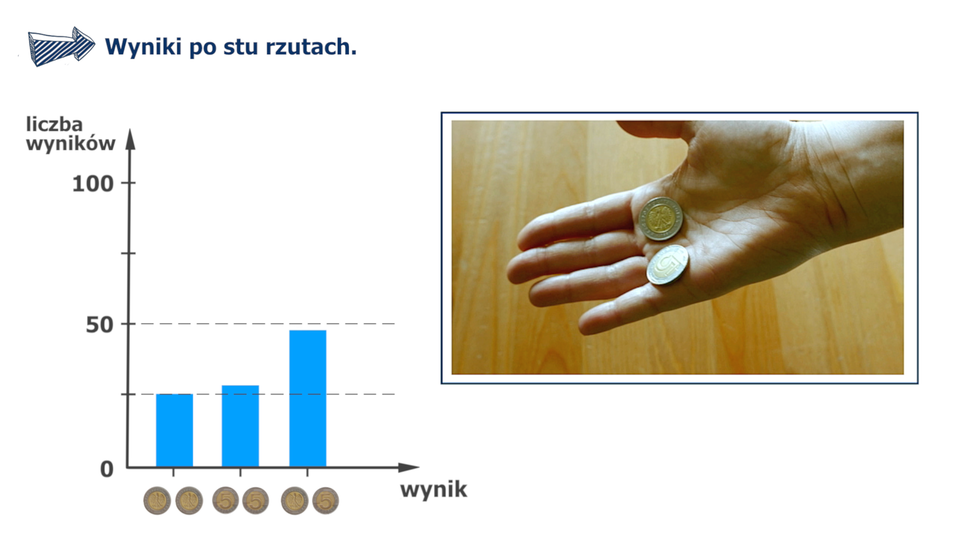
Film dostępny pod adresem /preview/resource/Rg0IeMgONyCQl
Animacja dotyczy rzutu dwoma identycznymi monetami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
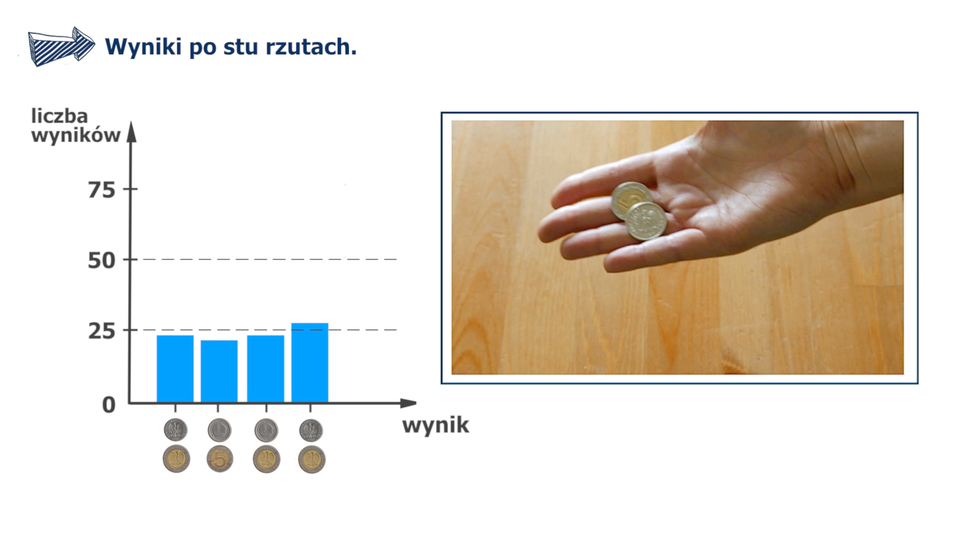
Film dostępny pod adresem /preview/resource/RZ29n0O3mEm8h
Animacja dotyczy rzutu dwoma różnymi monetami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
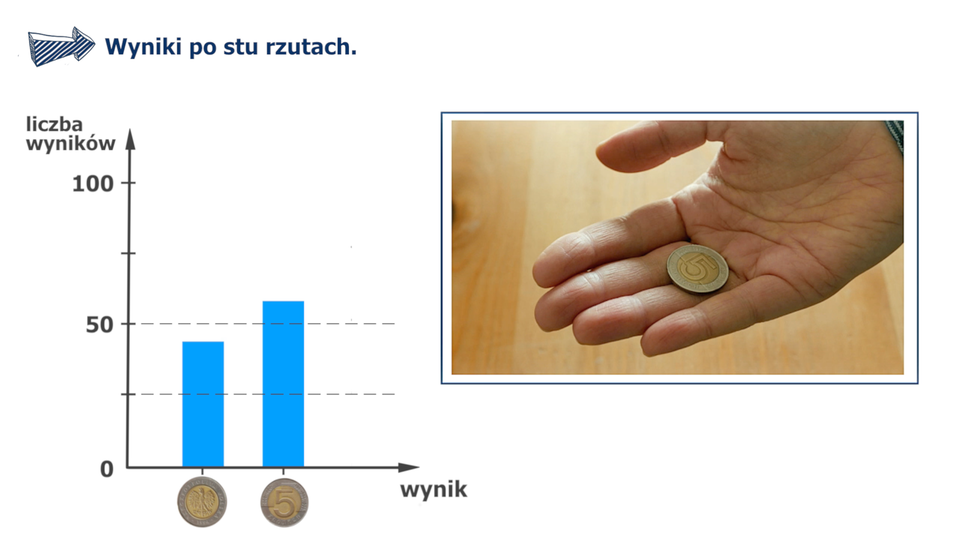
Film dostępny pod adresem /preview/resource/RXHxczROhHyrh
Animacja dotyczy rzutu jedną monetą, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
Wykonaj rzutów monetą. Porównaj swoje wyniki z wynikami przedstawionymi w Przykładzie .
Czy stwierdzenia sformułowane w filmie są prawdziwe dla Twoich wyników?
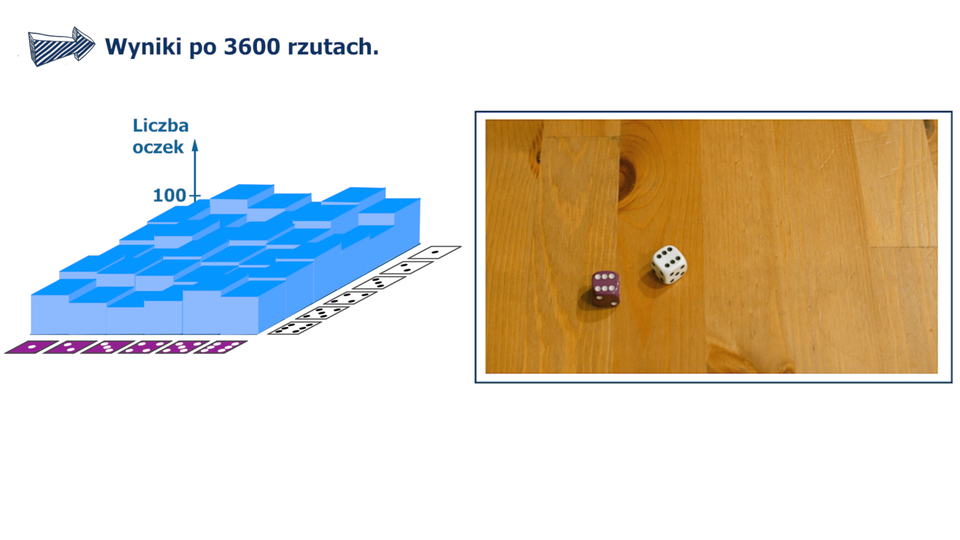
Film dostępny pod adresem /preview/resource/R8jXF43Qe6AON
Animacja dotyczy rzutu dwoma kostkami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu kostkami.
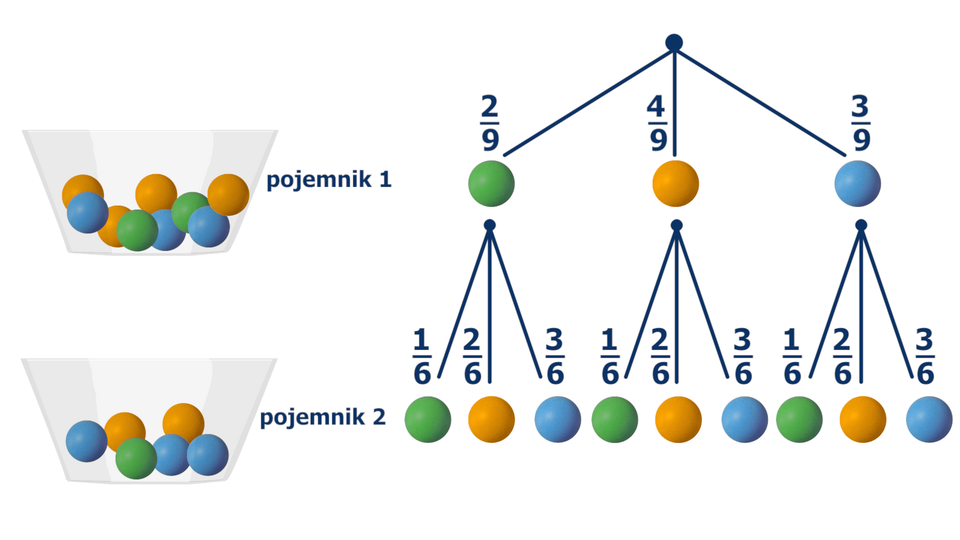
Film dostępny pod adresem /preview/resource/RcuTrTcBwwe2H
Animacja dotyczy losowania kul z dwóch pojemników. W pojemnikach znajdują się kule różnego koloru. Po prawej stronie wyświetla się drzewko przedstawiające prawdopodobieństwa wylosowania danego koloru kuli.

Film dostępny pod adresem /preview/resource/RjCkmcufP0rag
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić bluzki, niekoniecznie w tych samych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/R6JfSCvbrlOct
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić bluzki, w różnych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/R1FsEGWtJqY49
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić dwie bluzki, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/RY6mVoEjzcqLU
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić dwie bluzki, w różnych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/RfZYbeEJL5Fqu
Animacja przedstawia sposoby na zajęcia miejsc przy dwuosobowych, trzyosobowych oraz czteroosobowych stolikach. Po prawej stronie wyświetlają się sposoby umiejscowienia osób.
Reguła mnożenia
Liczba par elementów, w których pierwszy element pary można wybrać na sposobów, a drugi element pary na sposobów jest równa .
Regułę mnożenia można uogólnić dla trzech, czterech elementów.
Kuba postanowił zjeść obiad w stołówce szkolnej. Na ile sposobów Kuba może wybrać posiłek, jeżeli dziś ma ochotę na zupę, drugie danie i deser?
Menu stołówki:
Do wyboru są trzy zupy: barszcz czerwony, pomidorowa i rosół.
Do wyboru są cztery dania główne: makaron, pierogi, kotlet schabowy i pieczeń.
Do wyboru są dwa desery: szarlotka i ciasto czekoladowe.
Ile jest sposobów wyboru obiadu?
Trzy razy cztery razy dwa równa się dwadzieścia cztery możliwości, gdzie kolejne składniki mnożenia odpowiadają ilości rodzajów zup, dań głównych i deserów.
Z reguły mnożenia wynika,że Kuba może wybrać posiłek na sposoby.
Reguła dodawania
Jeżeli mamy dwa zbiory, jeden składający się z elementów, drugi składający się z elementów i żaden element nie powtarza się w obu zbiorach, to wybierając element z tych zbiorów, możemy to zrobić na sposobów.
Regułę dodawania można uogólnić na trzy, cztery zbiory.
Regułę dodawania stosujemy przy wyborze typu albo‑albo.
Kuba postanowił zjeść obiad w stołówce szkolnej. Na ile sposobów Kuba może wybrać posiłek, jeżeli dziś ma ochotę na zupę i drugie danie, albo drugie danie i deser?
możliwości
Menu stołówki:
Do wyboru są trzy zupy: barszcz czerwony, pomidorowa i rosół.
Do wyboru są cztery dania główne: makaron, pierogi, kotlet schabowy i pieczeń.
Do wyboru są dwa desery: szarlotka i ciasto czekoladowe.
Ile jest sposobów wyboru obiadu?
Trzy razy cztery razy plus cztery razy dwa równa się dwanaście plus osiem równa się dwadzieścia możliwości. Pierwszy iloczyn odpowiada ilości możliwości wyboru zupy i dania głównego, drugi iloczyn odpowiada ilości możliwości wybory dania głównego i deseru.
Z reguły mnożenia i reguły dodawania wynika, że Kuba może wybrać posiłek na sposobów.
Rzucamy jednokrotnie sześcienną kostką do gry. Połącz w pary nazwy zdarzeń z ich prawdopodobieństwami.
<math><mfrac><mn>2</mn><mn>3</mn></mfrac></math>, <math><mfrac><mn>1</mn><mn>6</mn></mfrac></math>, <math><mfrac><mn>1</mn><mn>2</mn></mfrac></math>, <math><mn>1</mn></math>, <math><mfrac><mn>1</mn><mn>3</mn></mfrac></math>
| A:Wyrzucimy nie mniej niż trzy oczka | |
| B:Wyrzucimy liczbę oczek podzielną przez trzy | |
| C:Wyrzucimy liczbę oczek będącą liczbą pierwszą | |
| D:Wyrzucimy liczbę oczek nie większą niż sześć | |
| E:Wyrzucimy liczbę oczek nie większą niż 1 |
- Prawdopodobieństwo zdarzenia, że suma oczek na obu kostkach będzie liczbą większą od , wynosi .
- Prawdopodobieństwo zdarzenia, że iloczyn oczek na obu kostkach będzie liczbą podzielną przez , wynosi .
- Prawdopodobieństwo zdarzenia, że liczba oczek na pierwszej kostce jest większa niż na drugiej kostce, wynosi .
- Prawdopodobieństwo zdarzenia, że liczba oczek na pierwszej kostce będzie parzysta, a liczba oczek na drugiej kostce będzie podzielna przez trzy, wynosi .
- 1
Kamila: "Prawdopodobieństwo, że podczas losowania z urny dwóch kul wylosujemy kulę białą lub niebieską, wynosi ".
Bartek: "Prawdopodobieństwo, że za drugim razem wylosujemy kulę białą jest mniejsze lub równe prawdopodobieństwu, że wylosujemy kulę czarną".
Kinga: "Prawdopodobieństwo, że za drugim razem wylosujemy kulę czarną, jeżeli za pierwszym razem wylosowaliśmy kulę zieloną, wynosi ".
Maciek: "Prawdopodobieństwo, że wylosujemy kulę czarną jest większe od tego, że wylosujemy kulę zieloną lub niebieską".
Które z dzieci ma rację? Możliwe odpowiedzi: 1. Kamila, 2. Bartek, 3. Kinga, 4. Maciek
- Kamila
- Bartek
- Kinga
- Maciek
Rzucamy trzy razy monetą. Przeciągnij zdarzenia z dolnej sekcji do górnej, określając ich prawdopodobieństwa.
<math><msub><mi>A</mi><mo>1</mo></msub><mo>-</mo></math> wyrzucono co najmniej dwa orły., <math><msub><mi>A</mi><mo>3</mo></msub><mo>-</mo></math> wyrzucono co najmniej jedną reszkę., <math><msub><mi>A</mi><mo>6</mo></msub><mo>-</mo></math> wyrzucono dwie reszki i jednego orła., <math><msub><mi>A</mi><mo>5</mo></msub><mo>-</mo></math> wyrzucono nie więcej niż dwie reszki., <math><msub><mi>A</mi><mo>4</mo></msub><mo>-</mo></math> wyrzucono same orły lub same reszki., <math><msub><mi>A</mi><mo>2</mo></msub><mo>-</mo></math> wyrzucono dokładnie jedną reszkę.
W loterii jest losów, w tym wygrywających. Wyznacz prawdopodobieństwo zdarzenia, że druga osoba wylosuje los wygrywający, jeżeli:
osoba przed nią kupiła los przegrywający,
osoba przed nią kupiła los wygrywający,
Które z tych zdarzeń jest bardziej prawdopodobne?
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby spośród ankietowanych jest kolor niebieski, wynosi .. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby jest niebieski lub zielony, jest większe niż to, że ulubionym kolorem jest czerwony lub żółty.. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem dowolnie wybranej osoby jest żółty, jest dwukrotnie mniejsze od tego, że tym kolorem jest niebieski.. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby jest zielony, wynosi .. Możliwe odpowiedzi: Prawda, Fałsz
Ile wynosi prawdopodobieństwo, że losowo wybrana osoba otrzyma bilet z miejscem na parterze? Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłową odpowiedź. Odpowiedź: Prawdopodobieństwo to wynosi 1. , 2. , 3. , 4. .
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Niech będzie zbiorem wszystkich dodatnich liczb parzystych mniejszych od , - zbiorem wszystkich liczb pierwszych mniejszych od . Ile jest par , takich że i ?
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Niech będzie zbiorem dzielników liczby , - zbiorem wszystkich dodatnich liczb nieparzystych mniejszych od . Ile jest par , takich że i ?
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Ile jest kodów trzycyfrowych, gdzie żadna liczba nie może się powtarzać?
Odp. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Na zakończenie rozwiąż test podsumowujący, który sprawdza wiedzę z tego materiału.
Rachunek prawdopodobieństwa z kombinatoryką