Proporcjonalność prosta

Rq7VEs3HrVoEB

Klient, który kupuje kubki, wie, że koszt zakupionego towaru (o stałej cenie jednostkowej) zależy od liczby zakupionych kubków.

Rpj8c4J1ENBZm

Na ilustracji znajduje się pięć kubków w kolorze brązowym. Jeden jest po lewej stronie grafiki, a kolejne cztery znajdują się po prawej stronie. Przy pojedynczym kubku znajduje się cena dwanaście złotych. Cztery pozostałe kubki oznaczone są zieloną pętlą i znajduje się przy nich cena czterdzieści osiem złotych. — Źródło: dostępny w internecie: Pexels.com, licencja: CC BY-SA 3.0.

Czym więcej kubków kupimy, tym więcej zapłacimy. Powiemy, że kwota, którą należy zapłacić jest proporcjonalna do liczby zakupionych kubków.

Do sformułowania teorii proporcji, która wpłynęła znacząco na rozwój nauk matematycznych, przyczynił się Eudoksos, grecki matematyk, astronom, geograf i filozof (ur. ok. $408$ p.n.e.).

Współcześnie z zależnościami proporcjonalnymi spotykamy się na co dzień. Na przykład przygotowując tekst za pomocą komputera często korzystamy z czcionki kroju proporcjonalnego.

Czcionki takie odzwierciedlają naturalny kształt liter. Na przykład litera „i” jest znacznie węższa od litery „w”, ta natomiast jest szersza od litery „u”. W tekście złożonym z użyciem takiej czcionki napisy wyglądają naturalnie. Odległości między środkami sąsiednich znaków są różne (zmieniają się proporcjonalnie).

RlhAARLMl42ic

Ilustracja przedstawia litery i cyfry wykonane czcionką proporcjonalną.

Napis na ilustracji wzorowany jest na starożytnych łacińskich tekstach i można go przetłumaczyć jako „Nikt nie lubi bólu, nie poszukuje go i nie pożąda, po prostu dlatego, że to jest ból $\dots$ ”. Tekst jest stosowany do demonstracji krojów pisma, kompozycji kolumny itd.

W tym materiale przybliżymy wiadomości związane z proporcjonalnością prostą.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Ilustracja interaktywnaIlustracja interaktywna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Rozpoznasz wielkości wprost proporcjonalne.
Zilustrujesz graficznie zależność między wielkościami wprost proporcjonalnymi.
Dobierzesz model matematyczny do sytuacji z kontekstem realistycznym związanej z wielkościami wprost proporcjonalnymi.

Narysujemy kilka trójkątów równobocznych i wyznaczmy obwód każdego z nich.

Rig3DtyKxgYwM

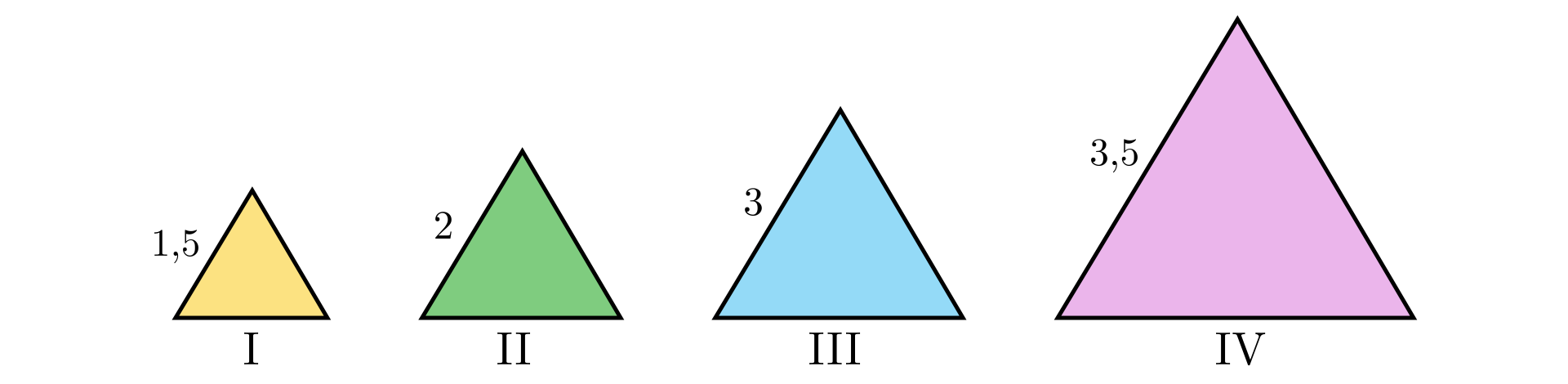
Ilustracja przedstawia cztery trójkąty równoboczne. Pierwszy trójkąt od lewej strony oznaczony jest rzymską cyfrą jeden. Ma wypełnienie w kolorze żółtym, a jego bok jest długości jeden i pięć dziesiątych. Drugi trójkąt od lewej strony oznaczony jest rzymską cyfrą dwa. Ma wypełnienie w kolorze zielonym, a jego bok jest długości dwa. Trzeci trójkąt od lewej strony oznaczony jest rzymską cyfrą trzy. Ma wypełnienie w kolorze niebieskim, a jego bok jest długości trzy. Czwarty trójkąt od lewej strony oznaczony jest rzymską cyfrą cztery. Ma wypełnienie w kolorze różowym, a jego bok jest długości trzy i pięć dziesiątych. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$L_{I} = 1, 5 + 1, 5 + 1, 5 = 4, 5$
$L_{II} = 2 + 2 + 2 = 6$
$L_{III} = 3 + 3 + 3 = 9$
$L_{IV} = 3, 5 + 3, 5 + 3, 5 = 10, 5$

Obwód trójkąta jest zależny od długości boku tego trójkąta.
Długość boku trójkąta $III$ jest $\frac{3}{1, 5} = 2$ razy większa od długości boku trójkąta $I$ – obwód trójkąta $III$ jest $\frac{9}{4, 5} = 2$ razy większy od obwodu trójkąta $I$ .

Długość boku trójkąta $IV$ jest $\frac{3, 5}{2} = 1, 75$ razy większa od długości boku trójkąta $II$ – obwód trójkąta $IV$ jest $\frac{10, 5}{6} = 1, 75$ razy większy od obwodu trójkąta $II$ .

Jeśli długość boku trójkąta zwiększymy, to obwód trójkąta zwiększy się tyle samo razy.

Obliczymy teraz stosunek obwodu każdego trójkąta do długości jego boku.

$\frac{4, 5}{1, 5} = 3$ $\frac{6}{2} = 3$ $\frac{9}{3} = 3$ $\frac{10, 5}{3, 5} = 3$

W każdym przypadku wyznaczony iloraz jest równy $3$ .

Zatem wraz ze zmianą długości boku trójkąta równobocznego zmienia się jego obwód w taki sposób, że stosunek obwodu do długości boku trójkąta jest stały i wynosi $3$ . Iloraz ten nazywamy współczynnikiem proporcjonalności.

Jeżeli literą $L$ oznaczymy obwód trójkąta równobocznego, a literą $a$ długość jego boku, to możemy zapisać:
$\frac{L}{a} = 3$ , czyli $L = 3 a$ .
Obwód trójkąta równobocznego jest trzy razy większy od długości boku tego trójkąta. Mówimy, że obwód jest wprost proporcjonalny do długości boku trójkąta. Liczba $3$ to współczynnik proporcjonalności.

R1YfDTUuEfque

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 1

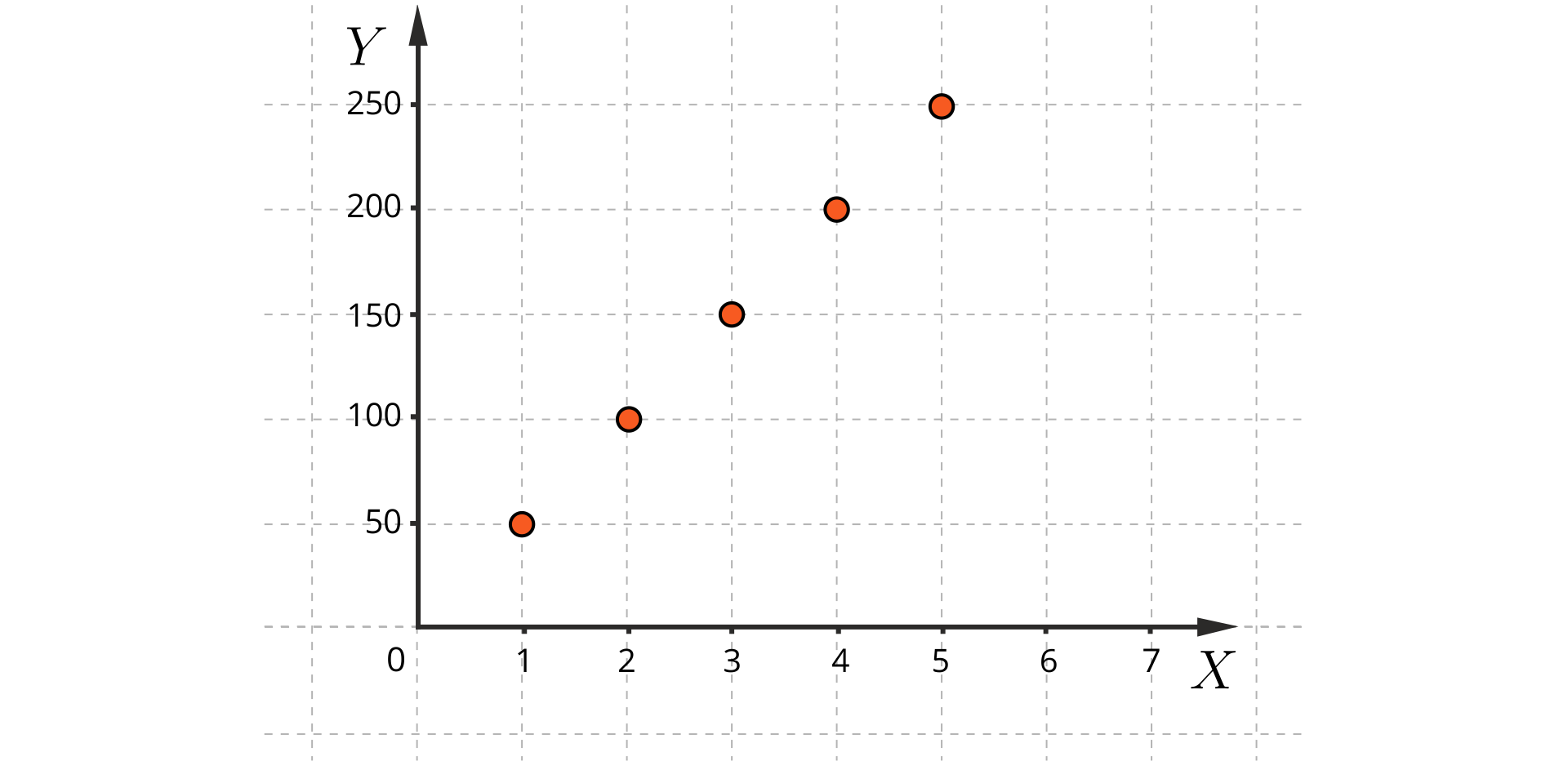
Pan Grzegorz przygotował powidła ze śliwek. Tabela przedstawia zależność między masą śliwek zakupionych przez pana Grzegorza w kolejnych dniach, a kwotą, którą za nie zapłacił (przy stałej cenie).

Masa śliwek (w $kg$ )	Koszt zakupu śliwek (w $zł$ )
$2$	$8$
$3$	$12$
$5$	$20$
$6$	$24$
$10$	$40$

Analizując tabelkę, wnioskujemy, że cena kilograma śliwek była równa.
$8 : 2 = 4 (zł)$ .
Im więcej śliwek pan Grzegorz kupił, tym więcej zapłacił. Koszt zakupu śliwek wzrasta tyle samo razy, ile razy wzrasta masa śliwek. Masa zakupionych śliwek i koszt zakupu są wielkościami wprost proporcjonalnymi.
Współczynnik proporcjonalności jest równy cenie śliwek.

Dwie wielkości dodatniewielkości wprost proporcjonalneDwie wielkości dodatnie są wprost proporcjonalne (w skrócie: proporcjonalne) wtedy, gdy wraz ze wzrostem jednej wielkości druga wielkość rośnie tyle samo razy.

Przykład 2

Pani Cecylia przygotowała na zimę kompoty z brzoskwiń. Tabela przedstawia zależność między masą brzoskwiń, a liczbą słoików potrzebnych do umieszczenia wykonanych z nich kompotów.

$x$ – masa brzoskwiń (w $kg$ )	$y$ – liczba potrzebnych słoików (w sztukach)
$3$	$6$
$4, 5$	$9$
$10, 5$	$21$
$12$	$24$

Wyznaczymy ilorazy liczb potrzebnych słoików, przez masę brzoskwiń.
$\frac{6}{3} = 2$ $\frac{9}{4, 5} = 2$ $\frac{21}{10, 5} = 2$ $\frac{24}{12} = 2$
Otrzymane ilorazy są równe i wynoszą $2$ .
Możemy zapisać:
$\frac{y}{x} = 2$ lub $y = 2 x$ .
Liczba słoików i masa brzoskwiń, to wielkości wprost proporcjonalne. Współczynnik proporcjonalności jest równy $2$ .

Dwie wielkości $x$ , $y$ proporcjonalność prostaDwie wielkości $x$ , $y$ są wprost proporcjonalne, gdy ich iloraz jest liczbą stałą. Tę stałą liczbę nazywamy współczynnikiem proporcjonalności.

\frac{y}{x} = a

$a$ – współczynnik proporcjonalności.
Możemy też zapisać: $y = a x$ .

Przykład 3

Odległość od miejscowości Anowo do miejscowości Benowo jest równa $312 km$ . Pan Adrian jedzie samochodem ze stałą prędkością. Samochód w ciągu kwadransa pokonuje drogę długości $12 km$ . Obliczymy, w ciągu ilu godzin pan Adrian dojedzie z miejscowości Anowo do miejscowości Benowo.

Rl8cpjn5gxKtB

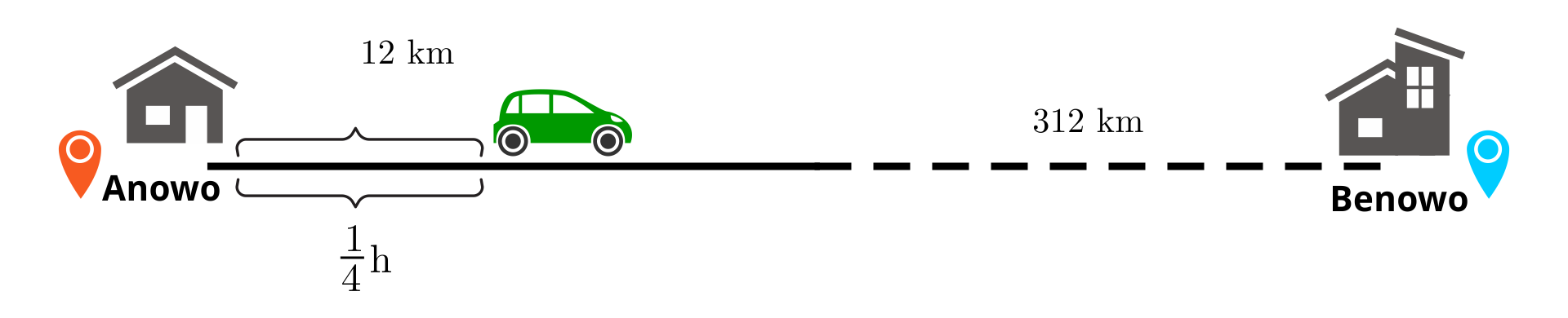
Ilustracja przedstawia dwie ikony domów, znajdujące się po przeciwnych stronach poziomej linii. Domek po lewej stronie znajduje się przy czerwonej pinezce z nazwą miejscowości "Anowo". Domek po prawej stronie znajduje się przy niebieskiej pinezce z nazwą miejscowości "Benowo". Odległość między dwoma miejscowościami wynosi trzysta dwanaście kilometrów. Ta wartość zapisana jest nad poziomą linią. Od Anowa do połowy drogi poprowadzona linia jest ciągła, natomiast od połowy drogi do Benowa linia jest przerywana. Po poziomej linii porusza się samochód w kolorze zielonym. Wyjechał z Anowa i porusza się w stronę Benowa. Między samochodem a miejscowością "Anowo" narysowana jest jedna klamra z podpisem dwanaście kilometrów oraz druga klamra z podpisem jedna czwarta godziny. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Długość drogi przebytej przez samochód jest wprost proporcjonalna do czasu jazdy, przy stałej prędkości.
Zatem im dłużej jedzie samochód, tym dłuższą pokona drogę. Obliczamy najpierw, ile kilometrów pokona pan Adrian w ciągu godziny, a następnie czas jazdy z Anowa do Benowa.

R9pQM0ezxxty0

Po lewej stronie ilustracji znajduje się napis "Czas jazdy (w godzinach)". Poniżej zapisany jest ułamek zwykły jedna czwarta. Pod ułamkiem jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 4". Pod grotem strzałki znajduje się liczba jeden. Poniżej zamieszczona jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 6,5". Poniżej znajduje się liczba 6,5. Po prawej stronie ilustracji znajduje się napis "Długość przebytej drogi (w kilometrach)". Poniżej zapisana jest liczba dwanaście. Pod liczbą jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 4". Pod grotem strzałki znajduje się liczba 48, a obok niej dopisek "w ciągu godziny". Poniżej zamieszczona jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 6,5". Poniżej znajduje się liczba 312, a obok niej dopisek "w ciągu 6,5 godzin". — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Odpowiedź:
Pan Adrian dojedzie do Benowa po $6, 5$ godzinach jazdy.

Przykład 4

Sprawdzimy, czy wielkości zapisane w tabelce są wprost proporcjonalnewielkości wprost proporcjonalnewprost proporcjonalne.

$x$	$y$
$2$	$3$
$6$	$9$
$8$	$12$
$10$	$25$

Obliczmy ilorazy $\frac{y}{x}$ .

\frac{3}{2} = 1, 5

\frac{9}{6} = 1, 5

\frac{12}{8} = 1, 5

\frac{25}{10} = 2, 5

\frac{3}{2} = \frac{9}{6} = \frac{12}{8} \neq \frac{25}{10}

Nie wszystkie ilorazy są równe – wielkości $x$ , $y$ nie są wprost proporcjonalne.

Przykład 5

Maszynistka przepisuje $2$ strony w ciągu $6$ minut. Obliczymy, ile stron przepisze maszynistka w ciągu $9$ minut.

Sposób $1$ :
Zauważmy, że $9$ możemy zapisać jako sumę liczb $6$ i $3$ . Ale $3$ to połowa liczby $6$ .

9 = 6 + 3

RiFuMyl5q1OQb

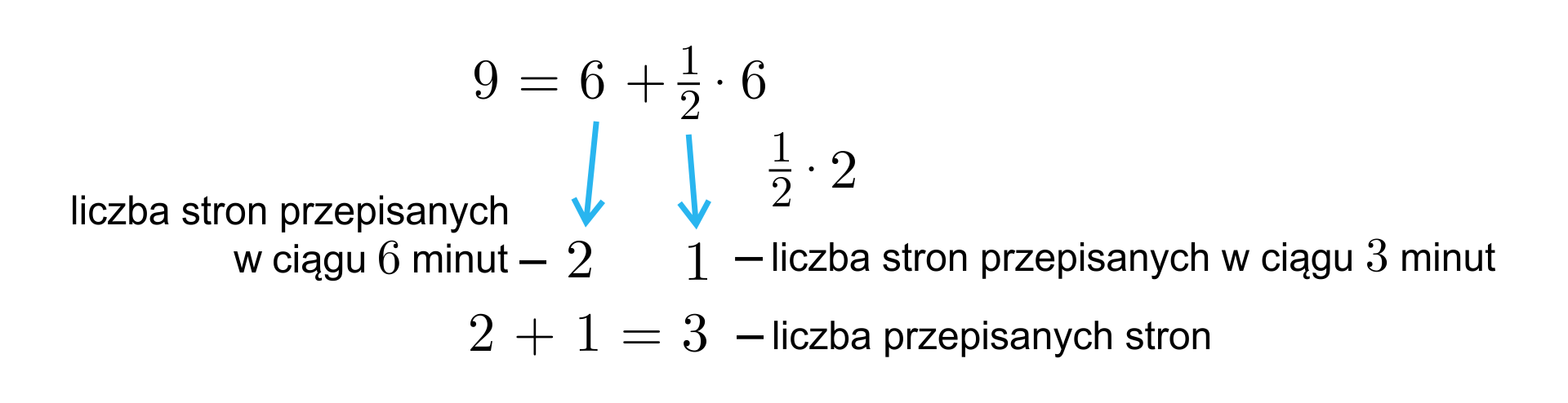
Na grafice znajduje się równanie matematyczne 9=6+12·6. Od liczby sześć, znajdującej się tuż za znakiem równości, poprowadzona jest pionowa strzałka ze zwrotem w dół. Pod grotem strzałki znajduje się napis "liczba stron przepisanych w ciągu sześciu minut - 2". Od ułamka 12 także poprowadzona jest pionowa strzałka ze zwrotem w dół. Po prawej stronie strzałki znajduje się zapis: "12 razy 2". Pod grotem strzałki znajduje się napis "1 - liczba stron przepisanych w ciągu trzech minut". W dolnej części grafiki umieszczone jest równanie dwa plus jeden jest równe 3, a obok niego tekst: "liczba przepisanych stron". — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeśli maszynistka w ciągu $6$ minut przepisze $2$ strony, to w ciągu połowy tego czasu przepisze $1$ stronę, czyli w ciągu $9$ minut przepisze $2 + 1 = 3$ strony.

Odpowiedź:
W ciągu $9$ minut maszynistka przepisze $3$ strony.

Sposób $2$ :
Obliczamy najpierw, ile stron maszynistka przepisze w ciągu minuty, a następnie w ciągu $9$ minut.

R17zgO5tym9Ys

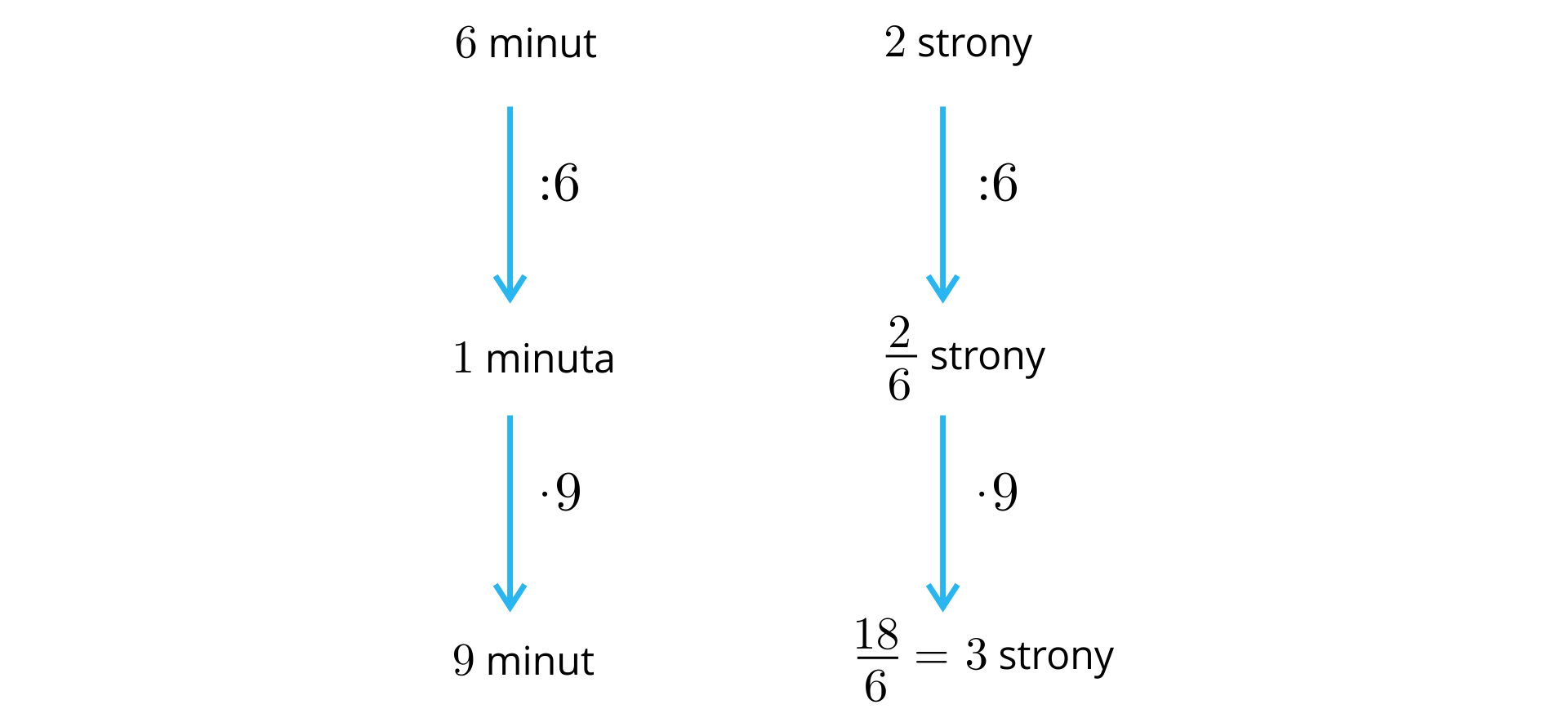
Po lewej stronie ilustracji znajduje się napis "6 minut". Pod napisem jest pionowa strzałka ze zwrotem w dół, w kolorze niebieskim, a po prawej stronie strzałki jest zapis "podzielić przez 6". Pod grotem strzałki znajduje się napis "1 minuta". Poniżej zamieszczona jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 9". Poniżej znajduje się napis "9 minut". Po prawej stronie ilustracji znajduje się napis "2 strony". Pod napisem jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "podzielić przez 6". Pod grotem strzałki znajduje się napis "26 strony". Poniżej zamieszczona jest pionowa strzałka ze zwrotem w dół, a po prawej stronie strzałki jest zapis "razy 9". Poniżej znajduje się napis "186 = 3 strony". — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Odpowiedź:
W ciągu $9$ minut maszynistka przepisze $3$ strony.

Sposób $3$ :
Oznaczmy:
$x$ – czas (w min),
$y$ – liczba przepisanych stron.
Liczba stron przepisanych przez maszynistkę i czas przepisania to wielkości wprost proporcjonalne. Współczynnik proporcjonalności jest równy $\frac{y}{x}$ .
Wtedy:

\frac{y}{x} = \frac{2}{6}

\frac{y}{x} = \frac{1}{3}

y = \frac{1}{3} x

Otrzymaliśmy wzór opisujący zależność między liczbą $y$ przepisanych stron, a czasem $x$ przepisywania.
Jeśli ten czas wynosi $9$ minut, to

y = \frac{1}{3} \cdot 9 = 3

Odpowiedź:
W ciągu $9$ minut maszynistka przepisze $3$ strony.

Sposób $4$ :
Oznaczmy:
$x$ – czas (w min),
$y$ – liczba przepisanych stron.
Liczba stron przepisanych przez maszynistkę i czas przepisywania to wielkości wprost proporcjonalne. Zależność między tymi wielkościami można opisać wzorem
$y = \frac{1}{3} \cdot x$ , gdzie $x > 0$ .
Sporządzamy tabelę częściową opisującą powyższą zależność.

$x$	$y$
$3$	$1$
$6$	$2$
$12$	$4$

Sporządzamy wykres tej zależności. Zaznaczamy na rysunku punkty $(3, 1)$ , $(6, 2)$ , $(12, 4)$ odpowiadające danym z tabeli.

RszbkPF2Uvx9a

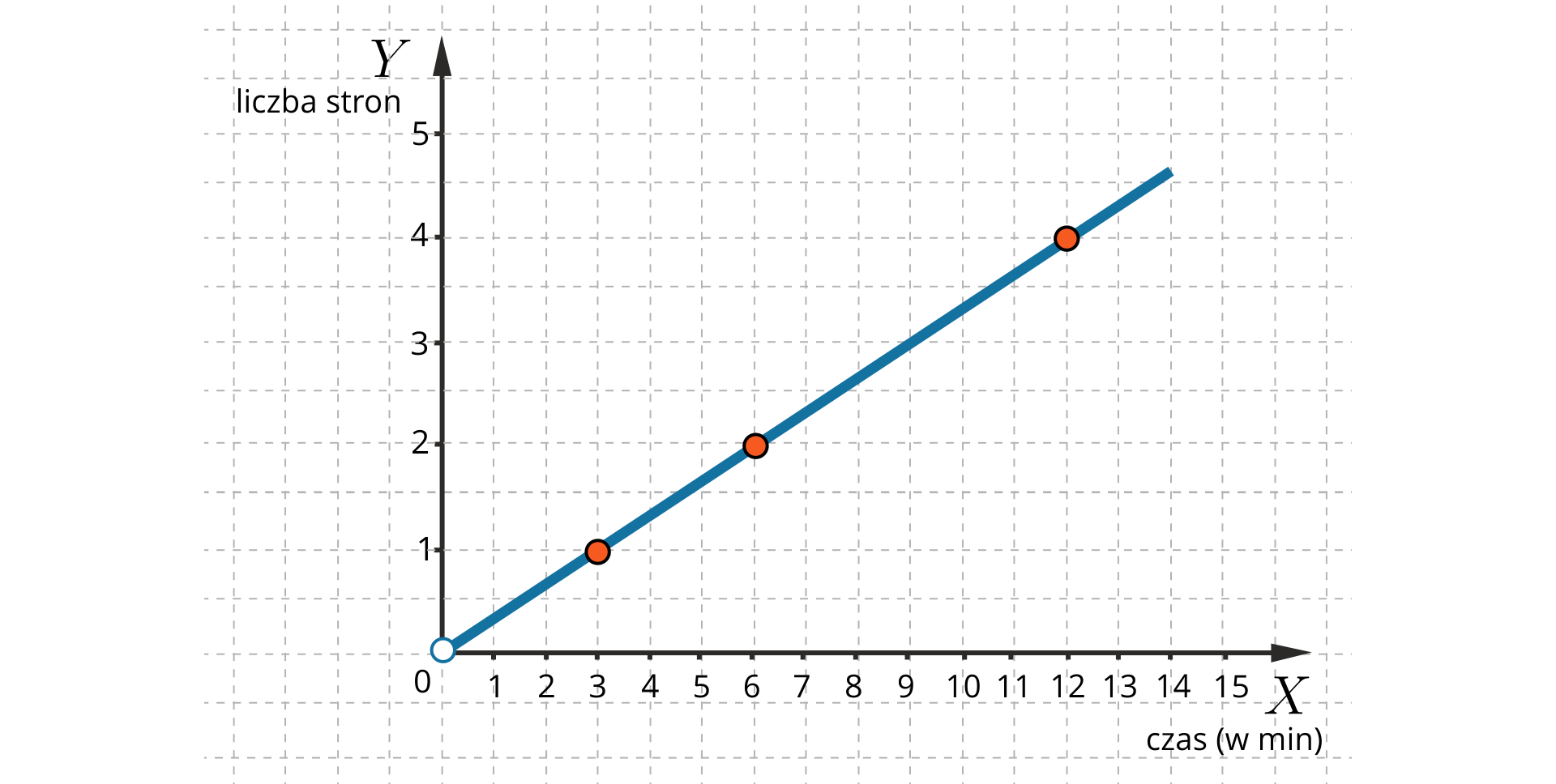
Grafika przedstawia układ współrzędnych. Oś pozioma "iks" ma zwrot w prawą stronę, natomiast oś pionowa "igrek" ma zwrot w górę. Oś pozioma podpisana jest jako czas (w minutach) i zaznaczone są na niej wartości od 0 do 15, rosnące w prawą stronę o jedną jednostkę. Oś pionowa podpisana jest jako liczba stron i zaznaczone są na niej wartości od 0 do 5, rosnące w górę o jedną jednostkę. W układzie zaznaczony jest punkt o współrzędnych 3,1, drugi o współrzędnych 6,2 oraz trzeci o współrzędnych 12,4. Punkty zaznaczone są kółeczkami w kolorze pomarańczowym. W układzie poprowadzona jest półprosta rozpoczynająca się w punkcie 0,0 i przechodząca przez wszystkie punkty zaznaczone na wykresie. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

W miejsce $x$ można podstawić dowolną liczbę dodatnią. Zatem wykres leży na półprostej o początku w punkcie $(0, 0)$ .
Z rysunku odczytujemy, że wciągu $9$ minut maszynistka przepisze $3$ strony.

R1IyTPjJA5AIB

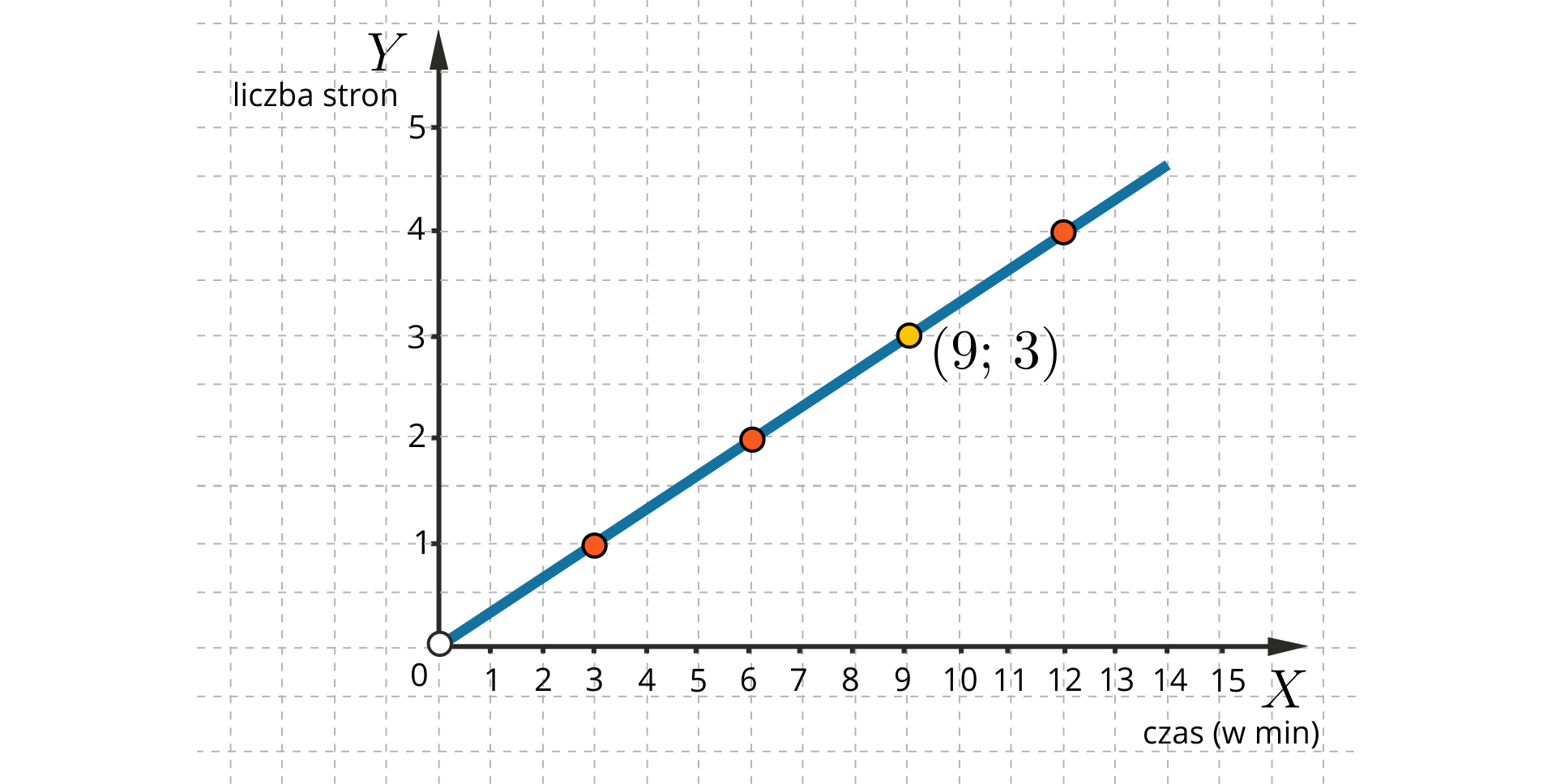
Odpowiedź:
W ciągu $9$ minut maszynistka przepisze $3$ strony.

Ważne!

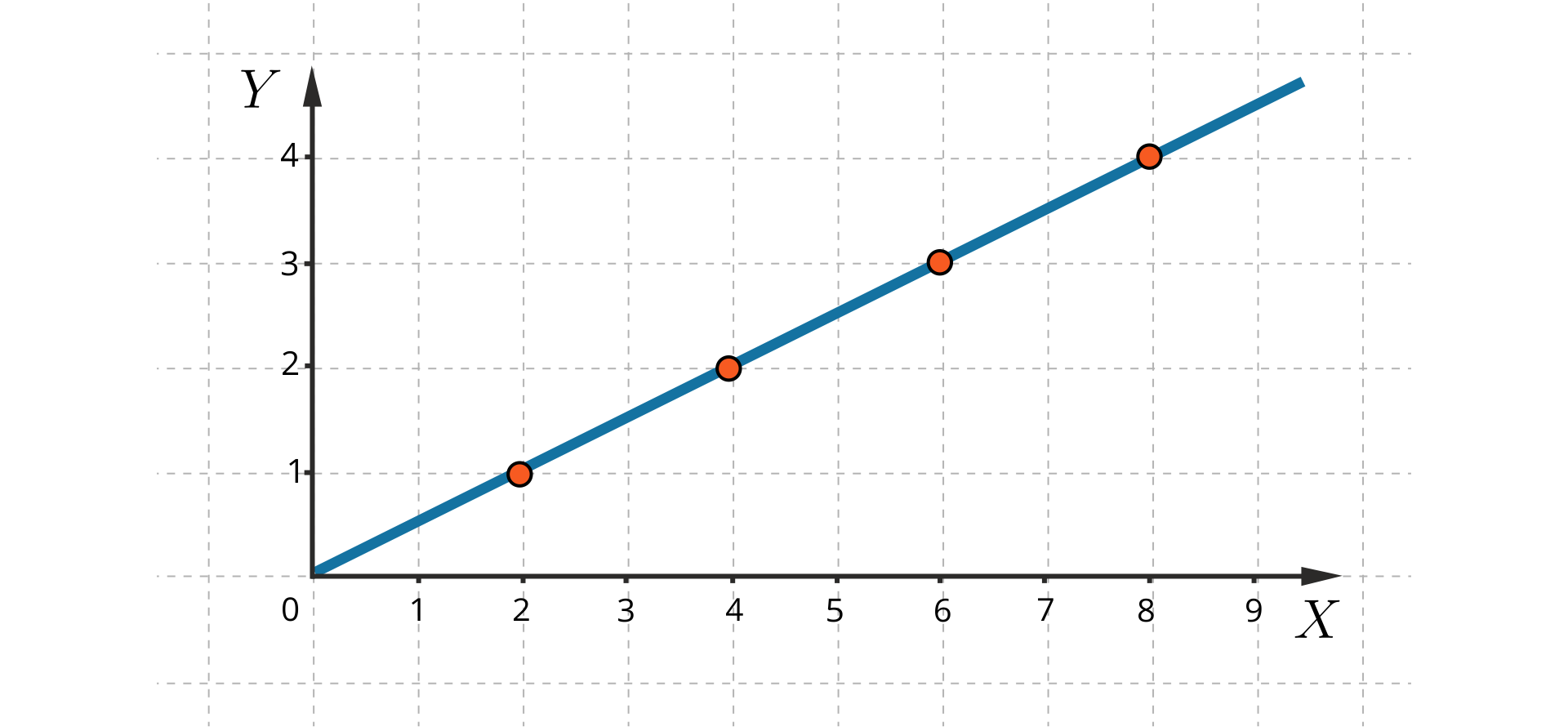
Zależność między dwiema wielkościami zmiennymi $x$ , $y$ określoną wzorem $y = a x$ , gdzie $a > 0$ nazywamy proporcjonalnością prostą. Liczbę $a$ nazywamy współczynnikiem proporcjonalności.
Wykres proporcjonalności prostej leży na półprostej.

Przykład 6

Obwód wielokąta foremnego jest wprost proporcjonalny do długości boku tego wielokąta. Zależność między obwodem $n$ – kąta foremnego $(y)$ , a długością jego boku $(x)$ wyraża wzór $y = n x$ , gdzie $n$ jest liczbą naturalną większą od $2$ i $x > 0$ .

Przykład 7

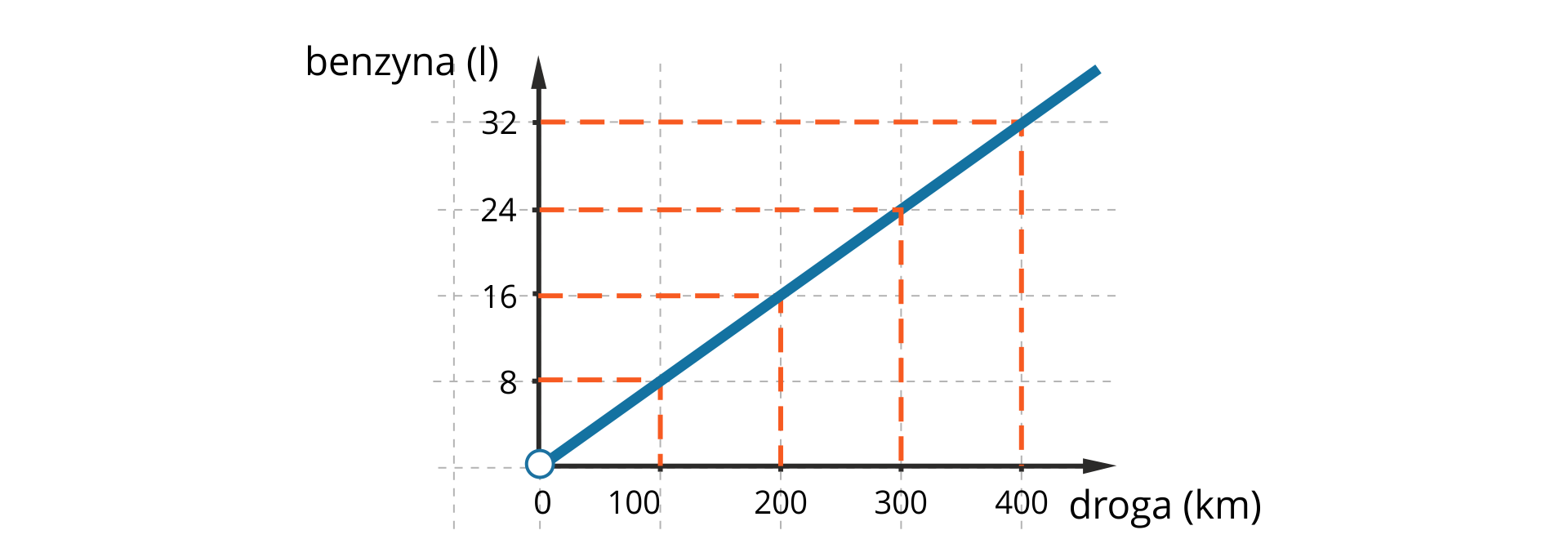
Ilość zużytej przez samochód benzyny jest wprost proporcjonalna do długości drogi przebytej przez ten samochód.
Rysunek przedstawia wykres tej proporcjonalności.

ROr6FRiRIH8wJ

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Pozioma oś zdefiniowana jest jako droga w kilometrach, a pionowa oś zdefiniowana jest jako benzyna. Na osi poziomej zaznaczono sto, dwieście, trzysta, czterysta. Na osi pionowej zaznaczono osiem, szesnaście, dwadzieścia cztery, trzydzieści dwa. W układzie zaznaczono prostą przechodzącą przez punkty o współrzędnych sto i osiem, dwieście i szesnaście, trzysta i dwadzieścia cztery oraz czterysta i trzydzieści dwa. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 8

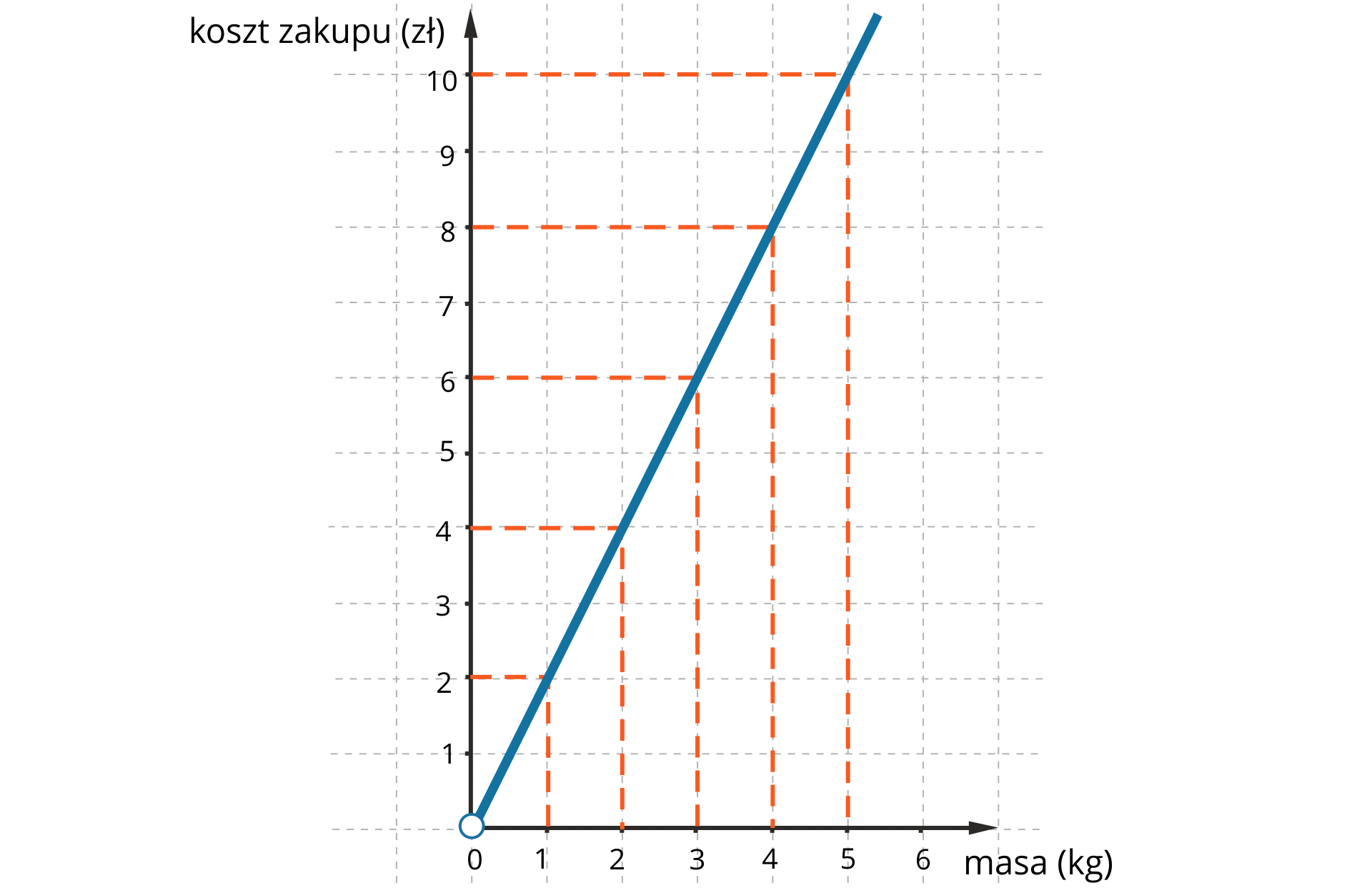
Koszt zakupu ogórków (przy stałej cenie) jest wprost proporcjonalny do masy zakupionych ogórków. Wykres tej proporcjonalności przedstawia rysunek.

RKP5dLt0WEmTl

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Pozioma oś zdefiniowana jest jako masa w kilogramach, a pionowa oś zdefiniowana jest jako koszt zakupów w złotych. Na osi poziomej zaznaczono liczby naturalne od zera do sześciu. Na osi pionowej zaznaczono liczby naturalne od jednego do dziesięciu. W układzie zaznaczono prostą przechodzącą przez punkty o współrzędnych jeden i dwa, dwa i cztery, trzy i sześć, cztery i osiem oraz pięć i dziesięć. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 9

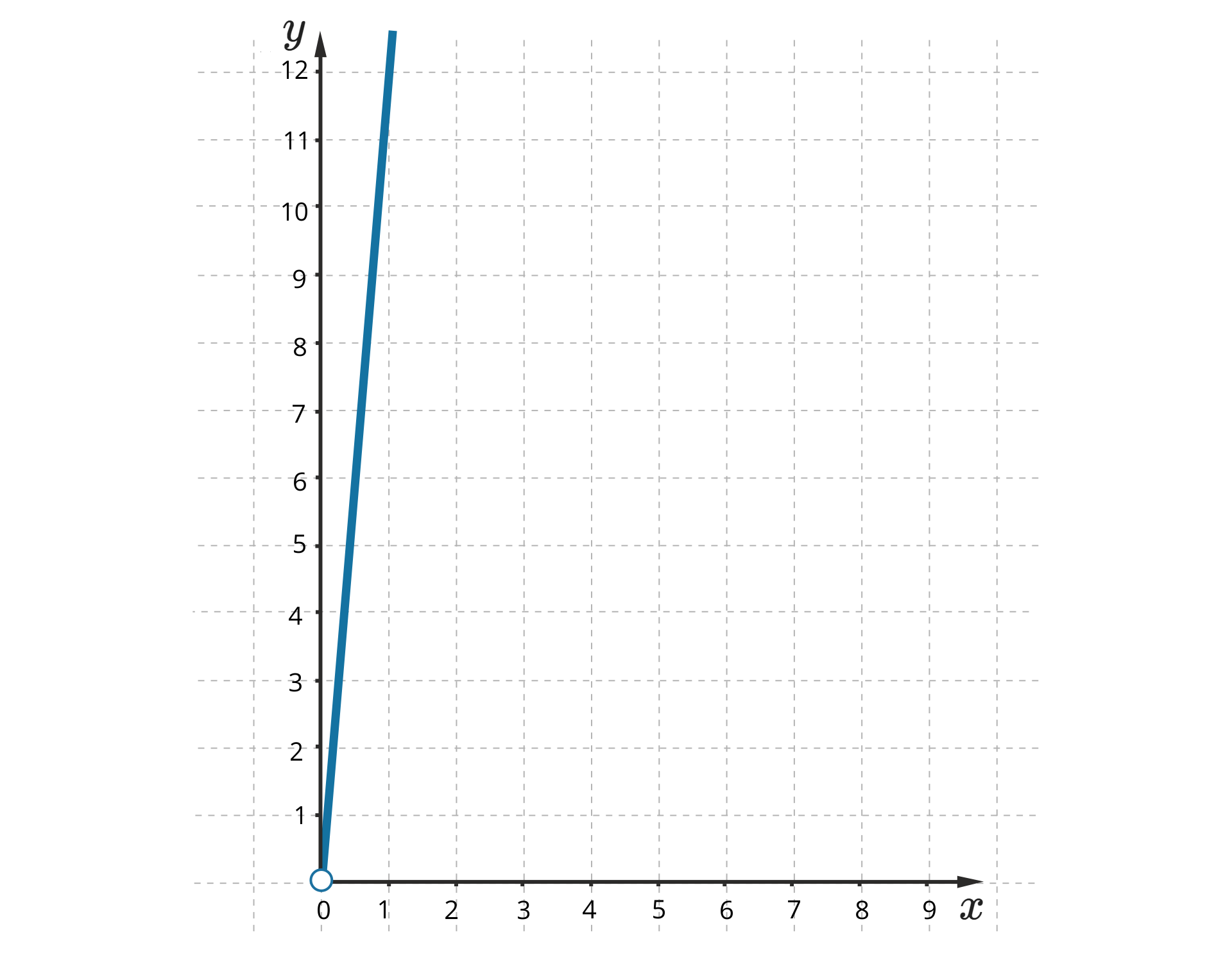
Rysunek przedstawia wykres proporcjonalności prostejproporcjonalność prostaproporcjonalności prostej określającej zależność sumy długości krawędzi sześcianu $(y)$ od długości jego krawędzi $(x)$ . Współczynnik proporcjonalności jest równy $12$ .

R1cH0tNTN2N0H

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Pozioma oś zdefiniowana jest jako iks, a pionowa oś zdefiniowana jest jako igrek. Na osi poziomej zaznaczono liczby naturalne od zera do dziewięciu. Na osi pionowej zaznaczono liczby naturalne od jednego do dwunastu. W układzie zaznaczono prostą przechodzącą przez punkty o zero i zero oraz jeden i dwanaście. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 10

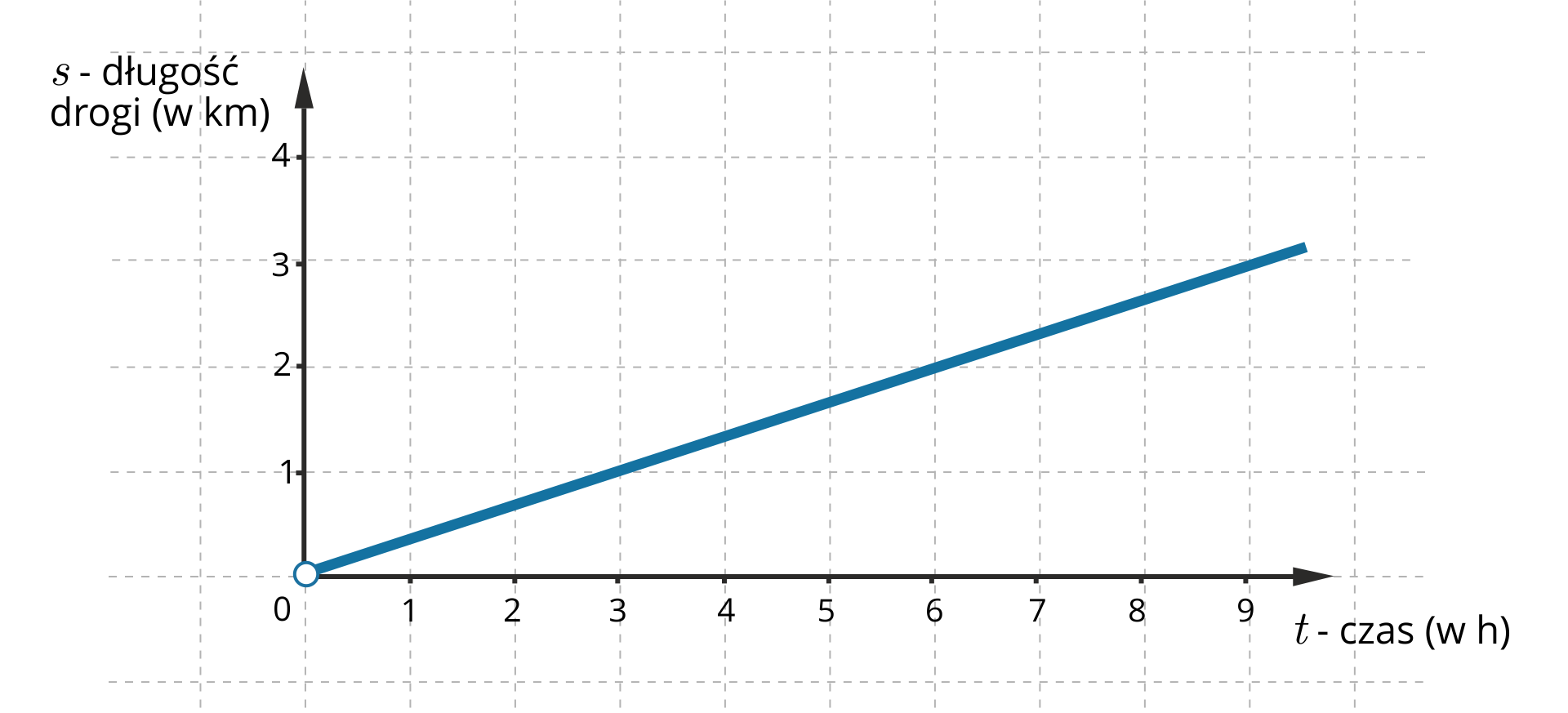
Rysunek przedstawia wykres zależności długości drogi $(s)$ przebytej przez pieszego od czasu $(t)$ , przy stałej prędkości $(v)$

s = v \cdot t

RppliDhhOmQHm

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Pozioma oś zdefiniowana jest jako t‑czas w godzinach, a pionowa oś zdefiniowana jest jako s - długość drogi w kilometrach. Na osi poziomej zaznaczono liczby naturalne od zera do dziewięciu. Na osi pionowej zaznaczono liczby naturalne od jednego do czterech. W układzie zaznaczono prostą przechodzącą przez punkty o współrzędnych trzy i jeden, sześć i dwa oraz dziewięć i trzy. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Notatki

RNYq1TvG0vVee

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ilustracja interaktywna

R1f2NhjERty2i

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Grafika przedstawia układ współrzędnych. Oś pozioma m ma zwrot w prawą stronę i przedstawia masę zakupionej mąki (w kilogramach). Zaznaczone są na niej wartości od 0 do 12, rosnące w prawą stronę o dwie jednostki. Oś pionowa duże K ma zwrot w górę i przedstawia koszt zakupu mąki (w złotych). Zaznaczone są na niej wartości od 0 do 8, rosnące co dwie jednostki. W układzie zaznaczone są dwa punkty o współrzędnych $2, 3$ i $4, 6$ . W układzie poprowadzona jest półprosta rozpoczynająca się w punkcie $0, 0$ i przechodząca przez wszystkie punkty zaznaczone na wykresie. Możliwe jest włącznie oraz wyłączenie podświetlania obu osi, półprostej oraz zaznaczonych punktów. Na grafice zaznaczono kolejnymi cyframi punkty interaktywne zawierające tekst wraz z nagraniem o treści tożsamej z tym tekstem. Cyfrą jeden oznaczony jest koniec półprostej. Pod nią znajduje się tekst: Jeśli masa zakupionej mąki się zwiększa, to również koszt zakupu się zwiększa. Cyfrą dwa oznaczony jest punkt o współrzędnych $2, 3$ . Pod nią znajduje się tekst: Stosunek kosztu zakupu do masy zakupionej mąki jest równy $\frac{3}{2} = 1, 5$ . Cyfrą trzy oznaczony jest punkt o współrzędnych $4, 6$ . Pod nią znajduje się tekst: Stosunek kosztu zakupu do masy zakupionej mąki jest równy $\frac{6}{4} = \frac{3}{2} = 1, 5$ . Cyfra cztery umieszczona jest po lewej stronie górnej części osi pionowej duże K. Pod nią znajduje się tekst: Koszt $K$ zakupu mąki przy cenie kilograma mąki równej $1, 50$ złotego wyraża się wzorem:
$K = 1, 50 m$ , gdzie $m$ – masa mąki w kilogramach. Koszt zakupu i masa mąki to wielkości wprost proporcjonalne. Współczynnik proporcjonalności jest równy cenie mąki, czyli wynosi jeden i pięć dziesiątych. Cyfry pięć i sześć znajdują się w prawym górnym rogu grafiki. Pod cyfrą pięć znajduje się tekst: Wykres opisuje, jak zmienia się koszt zakupu $K$ w zależności od masy $m$ zakupionej mąki, przy stałej cenie $c$ . Pod cyfrą sześć znajduje się podsumowanie: Zależność między dwoma wielkościami zmiennymi $x$ , $y$ określoną wzorem $y = a x$ , gdzie $a > 0$ nazywamy proporcjonalnością prostą. Liczbę $a$ nazywamy współczynnikiem proporcjonalności.

Polecenie 1

Długość drogi ( $s$ ) przebytej przez samochód i ilość zużytego przez samochód paliwa ( $x$ ) to wielkości wprost proporcjonalne. Na wykresie tej proporcjonalności leży punkt $(70, 595)$ . Zapisz wzór tej proporcjonalności.

RwFHFZv3Xv90m

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$s = a x$ , gdzie $a = \frac{595}{70} = 8, 5$
Wzór proporcjonalności: $s = 8, 5 x$ , gdzie $x > 0$

Polecenie 2

Rysunek przedstawia wykres proporcjonalności prostej. Odczytaj z wykresu współczynnik tej proporcjonalności.

R1IiS1OYGo2Yx

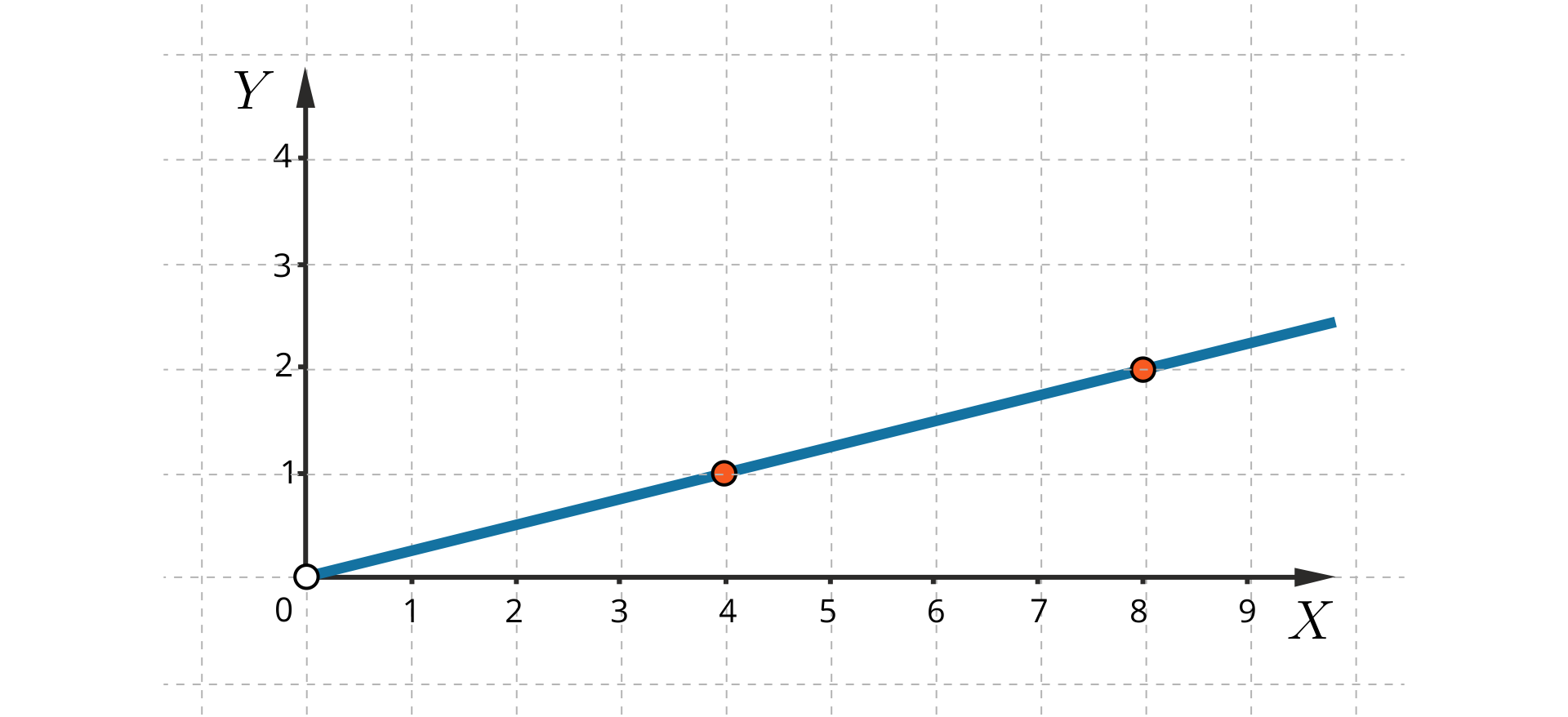
Grafika przedstawia układ współrzędnych. Oś pozioma "iks" ma zwrot w prawą stronę, natomiast oś pionowa "igrek" ma zwrot w górę. Na osi poziomej zaznaczone są wartości od 0 do 9, rosnące w prawą stronę o jedną jednostkę. Na osi pionowej zaznaczone są wartości od 0 do 4, rosnące w górę o jedną jednostkę. W układzie zaznaczony jest punkt o współrzędnych 4,1 oraz drugi o współrzędnych 8,2. W układzie poprowadzona jest prosta rozpoczynająca się w punkcie 0,0 i przechodząca przez wszystkie punkty zaznaczone na wykresie. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

W układzie współrzędnych prosta proporcjonalności przechodzi przez punkty $(0, 0)$ , $(4, 1)$ oraz $(8, 2)$ . Wyznacz współczynnik tej proporcjonalności.

RfVar1WqM2ceR

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zauważ, że punkt $(4, 1)$ należy do wykresu proporcjonalności.

Skorzystaj ze wzoru $y = a x$ .

$y = a x$ , stąd $a = \frac{y}{x}$

a = \frac{1}{4}

Współczynnik proporcjonalności jest równy $\frac{1}{4}$ .

Polecenie 3

Dwie wielkości są wprost proporcjonalne. Współczynnik proporcjonalności jest równy $4$ . Jedna z tych wielkości jest równa $5$ . Oblicz drugą z tych wielkości.

R1HFH4uyiDIHx

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Oznaczmy:
$a, b$ – wielkości wprost proporcjonalne.

Wtedy: $b = 4 a$ .

Pierwszy przypadek: $a = 5$ .

Wtedy

$b = 4 \cdot 5 = 20$ .

Drugi przypadek:

$b = 5$ .

Wtedy $5 = 4 a$ ,

$a = \frac{5}{4}$ .

Odpowiedź:
Te liczby to $5$ i $20$ lub $\frac{5}{4}$ i $5$ .

Zestaw ćwiczeń interaktywnych

R1GRK00WxE8w8

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 2

Wielkości $x$ , $y$ opisane w tabeli są wprost proporcjonalne.

$x$	$y$
$3, 4$	$23, 8$
$5$	$35$
$6, 2$	$k$

R1LbbwvAj3cnn

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 3

R1b5JKxhxHzdW

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 4

RQzHmzpKFCmKG

Uzupełnij zdania, wpisując odpowiednie liczby. Samochód pokonał trasę z miejscowości A do miejscowości B długości

372 km

ze średnią prędkością

62 \frac{km}{h}

. Pokonanie tej trasy zajęło mu (6) godzin.
Gdyby samochód jechał z prędkością o

31 \frac{km}{h}

większą, to w tym samym czasie pokonałby drogę długości (558)

km

. Jednocześnie na pokonanie trasy z A do B potrzebowałby o (2)

h

mniej.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wzór na drogę jest postaci: $s = V \cdot t$ .

R1UUAGhtlxXms

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

R110poiLRFYwa

Pani Sandra na przygotowanie zupy pomidorowej dla czteroosobowej rodziny potrzebuje

60 dag

mięsa wieprzowego.
Dopasuj odpowiedź do pytania. Ile kilogramów mięsa musi zakupić pani Sandra, na przygotowanie zupy pomidorowej dla

26

osób? Możliwe odpowiedzi: 1.

3, 9 kg

, 2.

2 kg

, 3.

1, 2 kg

, 4.

1, 8 kg

, 5.

2, 1 kg

Ile kilogramów mięsa musi zakupić pani Sandra, na przygotowanie zupy pomidorowej dla

12

osób? Możliwe odpowiedzi: 1.

3, 9 kg

, 2.

2 kg

, 3.

1, 2 kg

, 4.

1, 8 kg

, 5.

2, 1 kg

Ile kilogramów mięsa musi zakupić pani Sandra, na przygotowanie zupy pomidorowej dla

14

osób? Możliwe odpowiedzi: 1.

3, 9 kg

, 2.

2 kg

, 3.

1, 2 kg

, 4.

1, 8 kg

, 5.

2, 1 kg

le kilogramów mięsa musi zakupić pani Sandra, na przygotowanie zupy pomidorowej dla

8

osób? Możliwe odpowiedzi: 1.

3, 9 kg

, 2.

2 kg

, 3.

1, 2 kg

, 4.

1, 8 kg

, 5.

2, 1 kg

le kilogramów mięsa musi zakupić pani Sandra, na przygotowanie zupy pomidorowej dla

20

osób? Możliwe odpowiedzi: 1.

3, 9 kg

, 2.

2 kg

, 3.

1, 2 kg

, 4.

1, 8 kg

, 5.

2, 1 kg

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Pamiętaj, że $1 kg = 100 dag$ . Współczynnik proporcjonalności jest równy $\frac{0, 6}{4} = 0, 15$ .

Ćwiczenie 7

Wielkości $x$ , $y$ zapisane w tabeli są wprost proporcjonalne.

$x$	$y$
$2$	$1$
$4$	$2$
$6$	$3$
$8$	$4$

Sprządź wykres tej proporcjonalności.

Opisz wykres tej proporcjonalności.

R26anejj8O0b2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RlTJqAvNgxGIv

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zaznacz na rysunku punkty $(2, 1)$ , $(4, 2)$ , $(6, 3)$ , $(8, 4)$ i przeprowadź przez nie półprostą.

Przy opisie wykresu proporcjonalności pamiętaj o najważniejszych elementach jak podpis osi współrzędnych, zaznaczenie punktów w układzie współrzędnych.

Ćwiczenie 8

Przy cenie książki $50 zł$ za sztukę, koszt ( $y$ ) książek jest wprost proporcjonalny do ich liczby ( $x$ ).

Zapisz w postaci wzoru podaną zależność i przedstaw ją graficznie.

Zapisz w postaci wzoru podaną zależność i opisz jej wykres.

R9nAjqQM4ph29

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RRCEilT2mqaIc

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Szukany wzór:
$y = 50 x$ , gdzie $x = 1, 2, 3, \dots$

Opisaną zależność można przedstawić wzorem:
$y = 50 x$ , gdzie $x = 1, 2, 3, \dots$

Liczba książek wyraża się liczbą naturalną dodatnią. Zatem wykres będzie punktowy.

R162A8LU3GlAq

Grafika przedstawia układ współrzędnych. Oś pozioma "X" ma zwrot w prawą stronę, natomiast oś pionowa "Y" ma zwrot w górę. Na osi poziomej zaznaczone są wartości od 0 do 7, rosnące w prawą stronę o jedną jednostkę. Na osi pionowej zaznaczone są wartości od 0 do 250, rosnące w górę o pięćdziesiąt. W układzie zaznaczony jest punkt o współrzędnych 1, 50, drugi o współrzędnych 2, 100, trzeci o współrzędnych 3, 150, czwarty o współrzędnych 4, 200 oraz piąty o współrzędnych 5, 250. Punkty zaznaczone są kółeczkami w kolorze pomarańczowym. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Słownik

wielkości wprost proporcjonalne

dwie dodatnie wielkości są wprost proporcjonalne (w skrócie: proporcjonalne) wtedy, gdy wraz ze wzrostem jednej wielkości druga wielkość rośnie tyle samo razy.

proporcjonalność prosta

zależność między dwoma wielkościami wprost proporcjonalnymi $x$ , $y$ . Iloraz $\frac{y}{x}$ jest liczbą stałą. Tę stałą liczbę $a$ nazywamy współczynnikiem proporcjonalności:

\frac{y}{x} = a

Bibliografia

Szurek M., (2023), Spacery matematyczne. Zachwyć się liczbami i figurami!, Warszawa: Wydawnictwo K. Pazdro.