Przeczytaj
Pobierz przykładowe dane:
Oddzielanie danych rzeczywistych od prognozowanych na wykresie liniowym
Weźmy proste zestawienie danych. W arkuszu podaną mamy liczbę ludności w Poznaniu dla lat 1990‑2035. Dane jednak są rzeczywiste tylko do roku 2020. Od roku 2021 dane są prognozowaneprognozowanieprognozowane, informacja o tym została wprowadzona do arkusza.
Tak prezentuje się nasz arkusz z danymi:
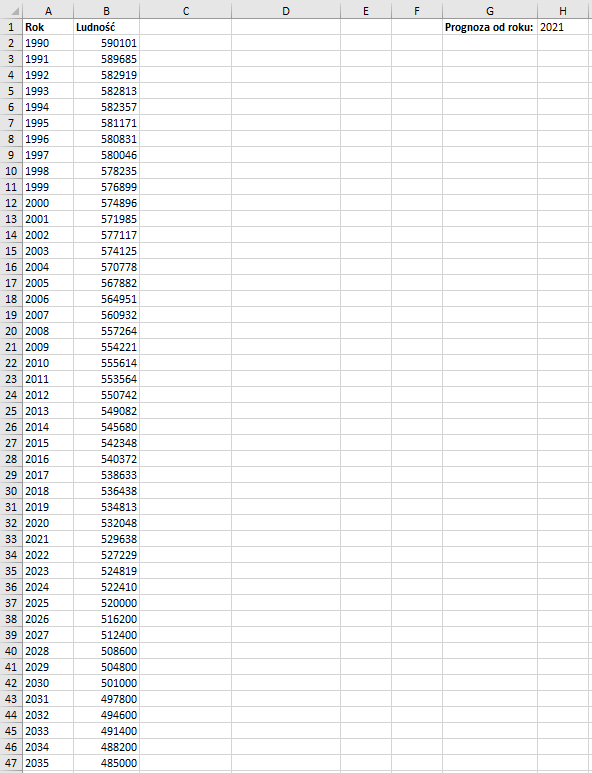
Na podstawie naszych danych stworzyliśmy wykres liniowy:
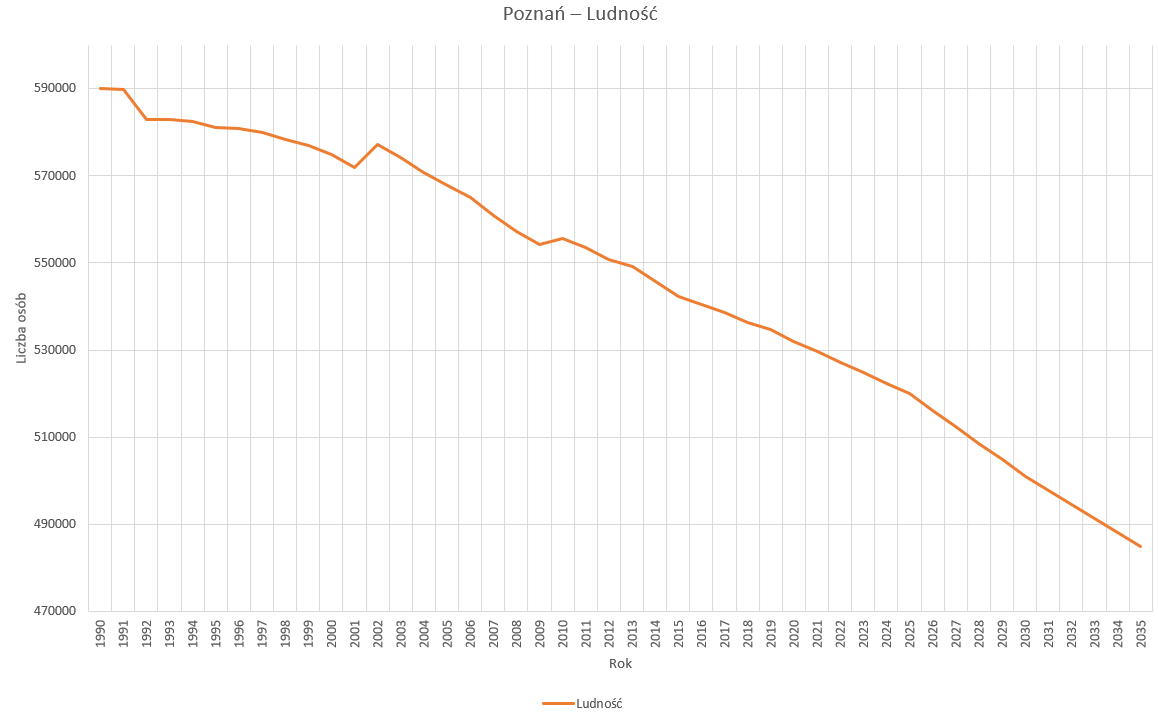
Widzimy jednak, że nie widnieją na nim podziały na dane rzeczywiste lub prognozowane.
Aby na podstawie tak zbudowanego zestawienia utworzyć czytelny wykres z wyraźnym oddzieleniem prognozy, należy wykonać następujące kroki:
Rozbudować tabelę o pomocnicze kolumny.
Wprowadzić odpowiednie formuły.
Zbudować wykres.
Sformatować serie danych.
Nadajmy kolumnom odpowiednie nazwy. W komórce C1 wpiszmy Wartości rzeczywiste, a w komórce D1 Wartości prognozowane.
W kolumnach C oraz D znajdą się formuły, których działanie będzie uzależnione od wartości podanych w komórce H1. Na tej podstawie dana wartość z kolumny B zostanie powtórzona.
Wartość w komórce H1 będzie nam więc służyła do określenia, od którego roku rozpoczynają się dane prognozowane.
W przygotowanych kolumnach można teraz wprowadzić formuły. Pierwsza będzie obsługiwać kolumnę C, a druga kolumnę D.
W tym celu:
W komórce
C2wpiszmy następującą formułę:=JEŻELI(A2<$H$1;B2;BRAK())Następnie skopiujmy ją do komórek leżących poniżej.
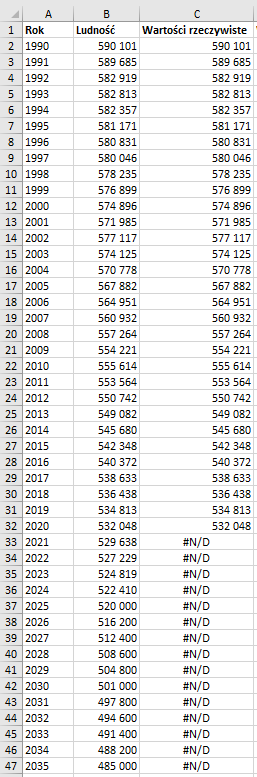
Łatwo dostrzec, że formuła zwraca poprawne dane tylko dla lat 1990‑2020, a w pozostałych wyświetla błąd. Błąd #N/D (niedostępna) informuje o tym, że formuła nie może znaleźć szukanego elementu, jednak jest to celowy zabieg, który pozwoli bezproblemowo zbudować czytelny wykres.
Nasza formuła składa się z funkcji JEŻELI(test_logiczny;[wartość_jeżeli_prawda];[wartość_jeżeli_fałsz]). W teście logicznym sprawdzamy, czy rok w kolumnie A jest mniejszy od roku w komórce H1, czyli tego, od którego rozpoczęliśmy prognozę. Jeśli tak, to funkcja zwróci wartość z komórki B2. Jeśli jednak test logiczny nie jest prawdziwy, to funkcja zwróci wynik funkcji BRAK(), a więc błąd #N/D.
Teraz wpiszmy do komórki
D2kolejną formułę:=JEŻELI(A2>=$H$1;B2;BRAK())Następnie skopiujmy ją do komórek leżących poniżej.
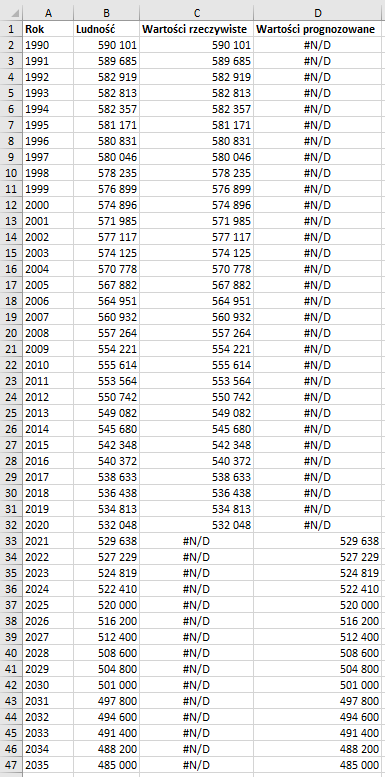
Łatwo dostrzec różnicę między wynikiem funkcji w kolumnie C, mimo iż same funkcje wyglądają bardzo podobnie. Jedyna różnica polega na zmianie samego testu logicznego, tym razem sprawdzamy, czy rok w kolumnie A jest większy lub równy od tego w komórce H1, czyli tego, od którego rozpoczęliśmy prognozę.
Stwórzmy nowy wykres liniowy na podstawie nowo utworzonych danych. Seriami danych będą kolumny C i D, a etykietami osi poziomej – kolumna A. Nadajmy odpowiednie tytuły osiom i samemu wykresowi, a następnie w menu Formatowanie osi przeskalujmy oś pionową, zmieniając jej granice od 470000 do 600000.
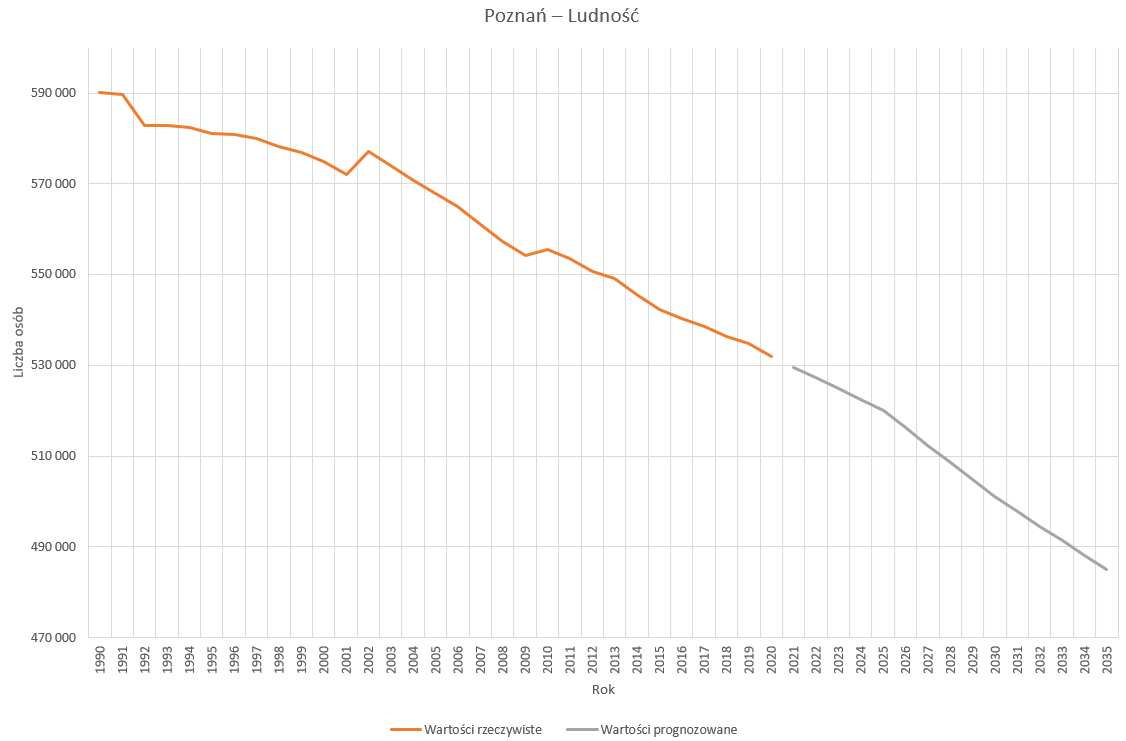
Teraz dodatkowo możemy zmienić kolory naszych serii, dla wartości rzeczywistych niech będzie to zielony, a dla prognozowanych czerwony.
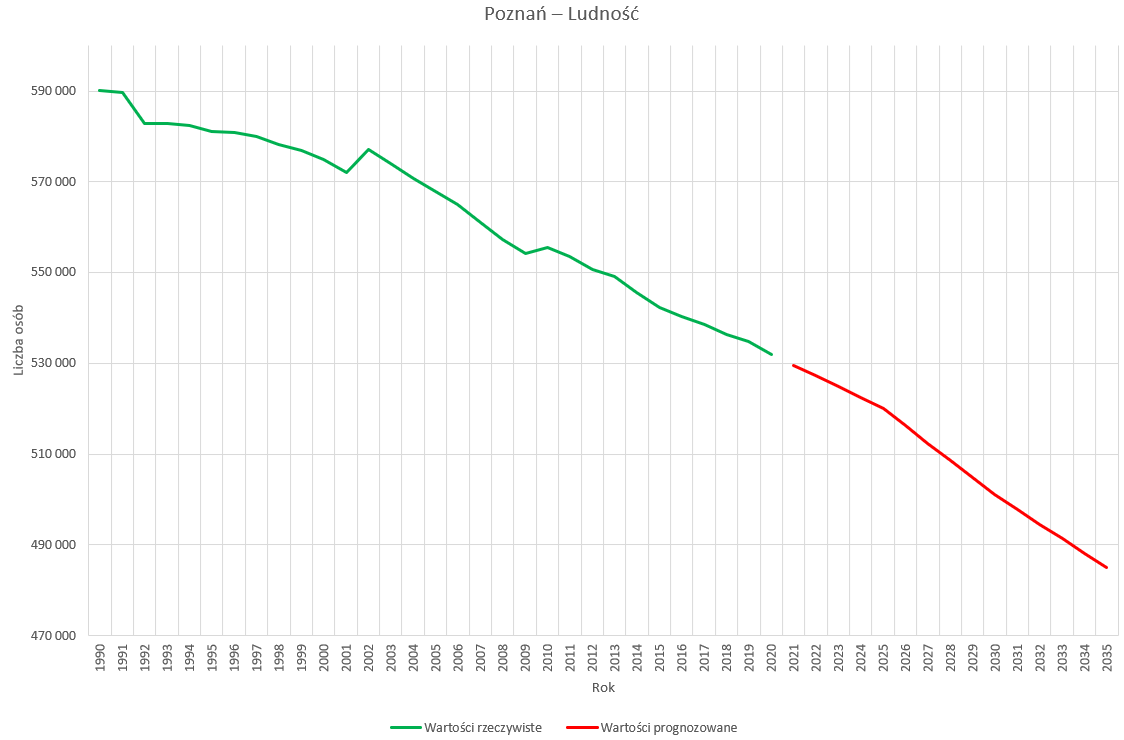
Jak widzimy, z takiego wykresu łatwo możemy odczytać wszystkie potrzebne nam dane, a także łatwo znajdziemy wartości rzeczywiste i prognozowane.
Tak prezentuje się nasz arkusz z danymi:
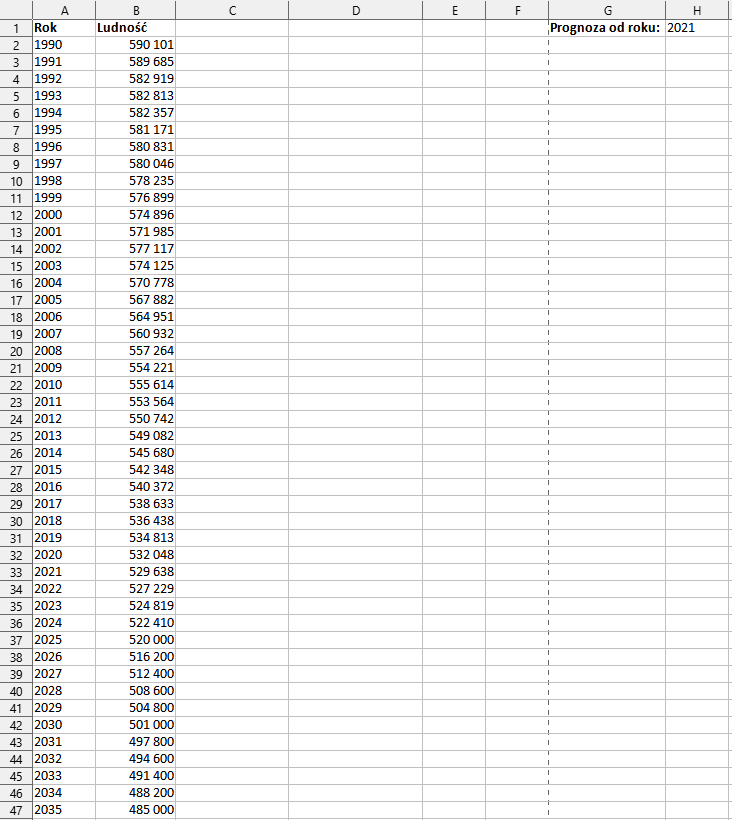
Na podstawie naszych danych stworzyliśmy już wykres liniowy:
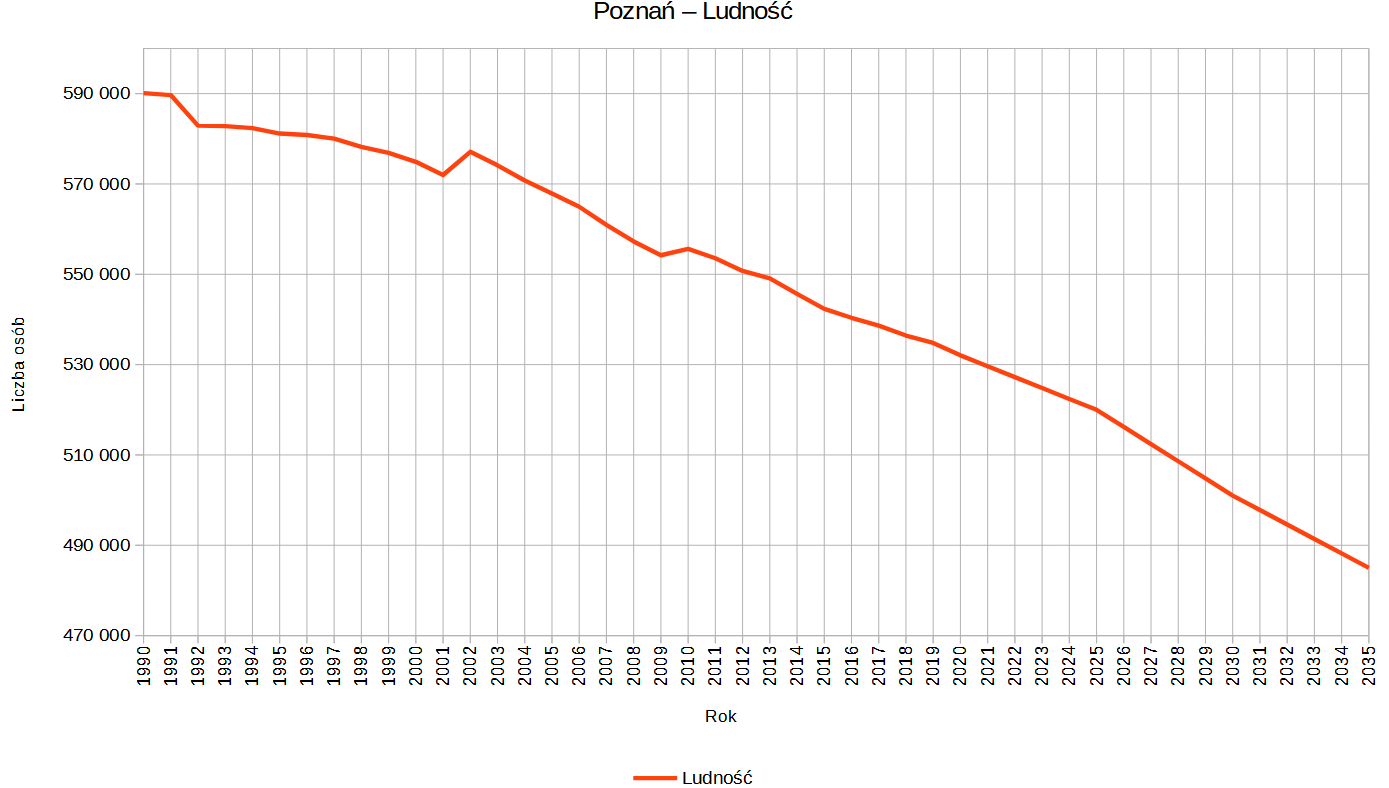
Widzimy jednak, że nie widnieją na nim podziały na dane rzeczywiste lub prognozowane.
Aby na podstawie tak zbudowanego zestawienia utworzyć czytelny wykres z wyraźnym oddzieleniem prognozy, należy wykonać następujące kroki:
Rozbudować tabelę o pomocnicze kolumny,
Wprowadzić odpowiednie formuły,
Zbudować wykres,
Sformatować serie danych.
Nadajmy kolumnom odpowiednie nazwy, w komórce C1 wpiszmy Wartości rzeczywiste, a w komórce D1 Wartości prognozowane.
W kolumnach C oraz D znajdą się formuły, których działanie będzie uzależnione od wartości podanych w komórce H1. Na tej podstawie dana wartość z kolumny B zostanie powtórzona.
Wartość w komórce H1 będzie nam więc służyła do określenia, od którego roku rozpoczynają się dane prognozowane.
W przygotowanych kolumnach można teraz wprowadzić formuły. Pierwsza będzie obsługiwać kolumnę C, a druga kolumnę D.
W tym celu:
W komórce
C2wpiszmy następującą formułę:=JEŻELI(A2<$H$1;B2;BRAK())Następnie skopiujmy ją do komórek leżących poniżej.
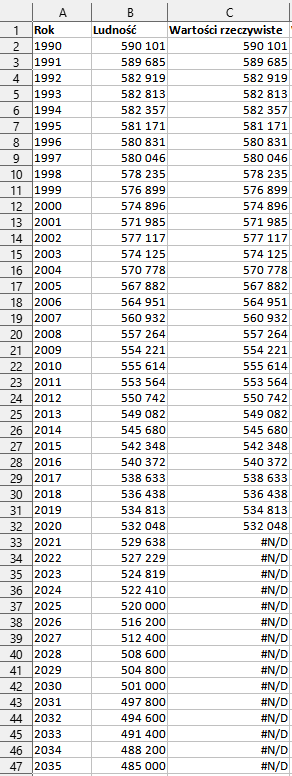
Łatwo dostrzec, że formuła zwraca poprawne dane tylko dla lat 1990‑2020, a w pozostałych wyświetla błąd. Błąd #N/D (nie dostępna) informuje o tym, że formuła nie może znaleźć szukanego elementu, jednak jest to celowy zabieg, który pozwoli bezproblemowo zbudować czytelny wykres.
Nasza formuła składa się z funkcji JEŻELI(test_logiczny;[wartość_jeżeli_prawda];[wartość_jeżeli_fałsz]). W teście logicznym sprawdzamy czy rok w kolumnie A jest mniejszy od roku w komórce H1, czyli tego, od którego rozpoczęliśmy prognozę. Jeśli tak, to funkcja zwróci wartość z komórki B2. Jeśli jednak test logiczny nie jest prawdziwy, to funkcja zwróci wynik funkcji BRAK(), a więc błąd #N/D.
Teraz wpiszmy do komórki
D2kolejną formułę:=JEŻELI(A2>=$H$1;B2;BRAK())Następnie skopiujmy ją do komórek leżących poniżej.
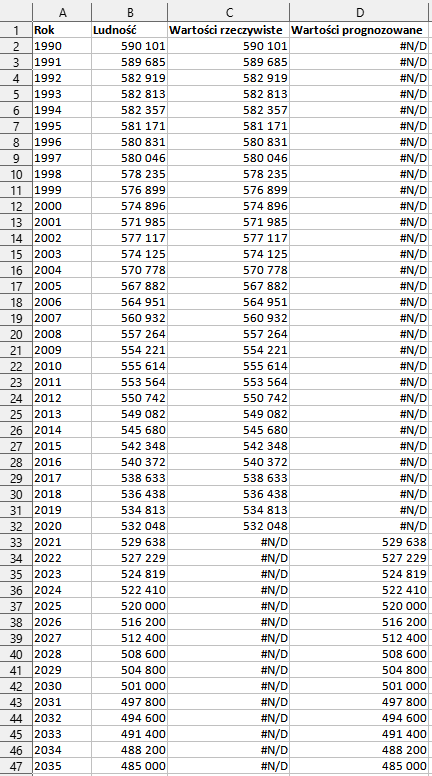
Łatwo dostrzec różnicę między wynikiem funkcji w kolumnie C, mimo iż same funkcje wyglądają bardzo podobnie. Jedyna różnica polega na zmianie samego testu logicznego, tym razem sprawdzamy, czy rok w kolumnie A jest większy lub równy od tego w komórce H1, czyli tego, od którego rozpoczęliśmy prognozę.
Stwórzmy nowy wykres liniowy na podstawie nowo utworzonych danych. Seriami danych będą kolumny C i D, a etykietami osi poziomej – kolumna A. Nadajmy odpowiednie tytuły osiom i samemu wykresowi, a następnie w oknie formatowania osi Oś Y, zakładka Skala, przeskalujmy oś pionową, zmieniając jej granice od 470000 do 600000.
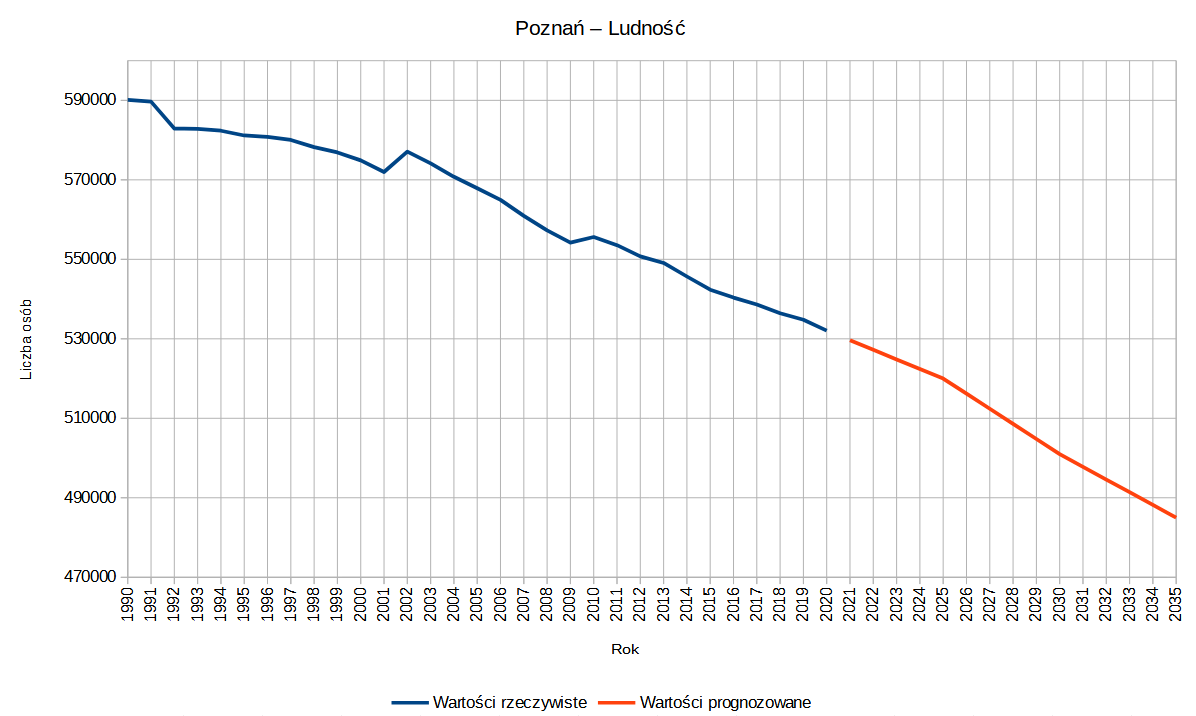
Teraz dodatkowo możemy zmienić kolory naszych serii, dla wartości rzeczywistych niech będzie to zielony, a dla prognozowanych czerwony.
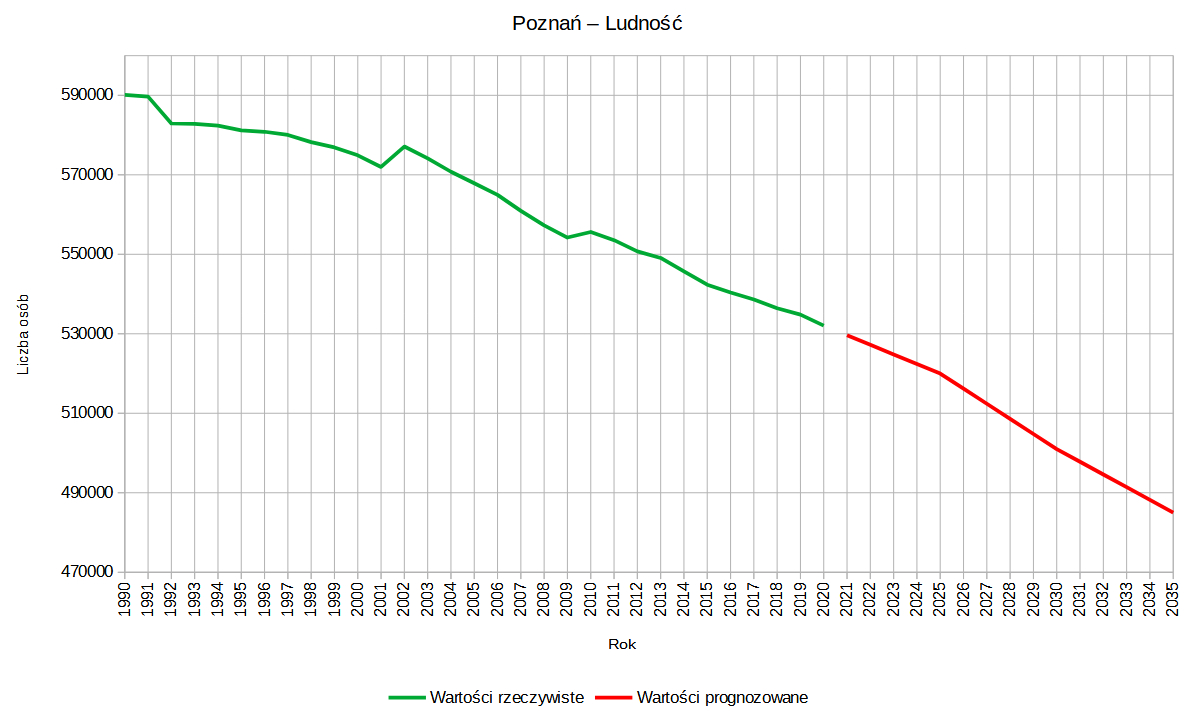
Jak widzimy, z takiego wykresu łatwo możemy odczytać wszystkie potrzebne nam dane, a także łatwo znajdziemy wartości rzeczywiste i prognozowane.
Słownik
racjonalne, naukowe, przewidywanie przyszłych zdarzeń, czyli wnioskowanie o zdarzeniach nieznanych na podstawie zdarzeń znanych