Przeczytaj
Funkcja jest równa funkcji , gdy dla każdego elementu spełniony jest warunek .
Równość funkcji i możemy zapisać symbolicznie:
Zwrot „dla każdego” nazywamy kwantfikatorem ogólnym (dużym) i oznaczamy symbolem .
Analizując definicję funkcji równych możemy zauważyć, że funkcje równefunkcje równe spełniają dwa warunki.
Warunek 1.
Dziedziny obu funkcji są takie same.
Warunek 2.
Dla tych samych argumentów funkcje przyjmują te same wartości.
W jaki sposób możemy sprawdzić równość dwóch funkcji liczbowych? Pokażemy to na kilku przykładach. Będziemy głównie korzystać z wykresów funkcji.
Funkcje i opisane są za pomocą wykresów.
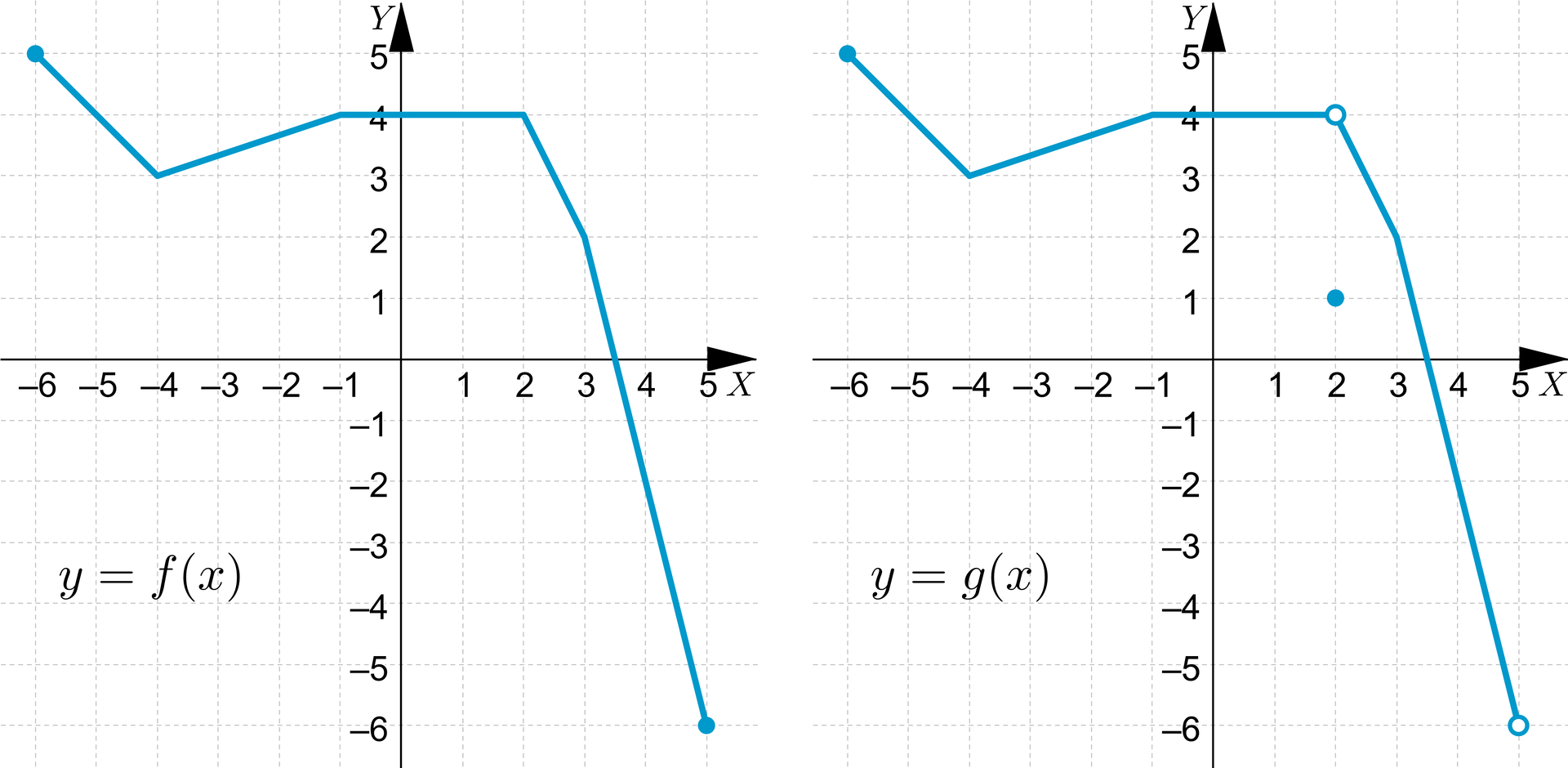
Sprawdzimy, czy funkcje te są równe.
Rozwiązanie:
Sprawdzimy, czy spełniony jest pierwszy warunek równości funkcji. W tym celu wyznaczymy dziedziny obu funkcji.
Funkcje i mają różne dziedziny.
Nie jest więc spełniony pierwszy warunek równości funkcji.
Zatem funkcje i nie są równe.
Funkcja opisana jest za pomocą zbioru par uporządkowanych.
.
Funkcja opisana jest za pomocą tabelki.
Sprawdzimy, czy te funkcje są równe.
Rozwiązanie:
Sprawdzimy, czy spełniony jest pierwszy warunek równości funkcji. Porównamy dziedziny obu funkcji.
,
.
Funkcje i mają różne dziedziny.
Nie jest więc spełniony pierwszy warunek równości funkcji.
Zatem funkcje i nie są równe.
Funkcja opisana jest za pomocą wzoru.
, gdy .
Funkcja opisana jest za pomocą wzoru.
, gdy .
Wykażemy, że funkcje i są równe.
Rozwiązanie:
Aby wykazać, że funkcje i są równe musimy udowodnić spełnienie obu warunków równości funkcji.
Warunek pierwszy jest spełniony, ponieważ dziedziny obu funkcji są takie same.
oraz
Sprawdzamy, czy jest spełniony warunek drugi.
Przekształcimy wzór opisujący funkcję .
Po usunięciu niewymierności z mianownika okazało się, że wzory opisujące funkcje i są identyczne.
Stąd wniosek, że dla dowolnego argumentu wartości funkcji i są jednakowe.
Zatem funkcje i są równe.
Zbadamy, czy funkcje i są równe.
Naszkicujemy wykresy tych funkcji i porównamy je.
Rozwiązanie:
Określimy dziedziny tych funkcji.
Zauważamy, że .
Stąd wniosek, że funkcje i nie są równe.
Wzór funkcji możemy zapisać w prostszej postaci: , gdy .
Stąd wniosek, że funkcja dla każdego przyjmuje wartość .
Funkcja przyjmuje wartość dla .
Naszkicujemy wykresy obu funkcji.

Analizując wykresy funkcji i możemy zauważyć, że różnią się one jednym punktem.
Stąd wniosek, że funkcje i nie są równe.
Wykażemy, korzystając z definicji, że funkcje i są równe.
, .
Rozwiązanie:
Wyznaczymy dziedziny obu funkcji.
Funkcja – zapiszemy wyrażenie znajdujące się w mianowniku wzoru funkcji w postaci iloczynowej.
Skorzystamy ze wzoru skróconego mnożenia na kwadrat różnicy dwóch wyrażeń.
Mianownik ułamka musi być liczbą różną od zera. Zapisujemy to w następującej postaci:
Stąd .
Po skróceniu wzór funkcji ma postać:
, gdy .
Dziedziną funkcji jest zbiór:
.
Możemy zauważyć, że spełniony jest pierwszy warunek równości funkcji:
.
Sprawdzimy, czy spełniony jest drugi warunek równości funkcji.
Po przekształceniu wzoru funkcji otrzymaliśmy wyrażenie algebraiczne, które jest identyczne jak wzór funkcji .
Okazało się, że wzory funkcji i są identyczne.
Stąd wynika, że dla dowolnego argumentu wartości funkcji i są jednakowe.
Funkcje i są równe.
Wykażemy, że funkcje i nie są równe, jeśli:
a) , ,
b) , .
Rozwiązanie:
Ad. a). Wyznaczymy dziedziny obu funkcji.
Dziedzina funkcji .
Mianownik ułamka musi być liczbą różną od zera.
Zapisujemy to w następującej postaci:
Zatem .
Dziedzina funkcji .
Mianownik ułamka musi być liczbą różną od zera.
Zapisujemy to w sposób następujący:
Zatem .
Możemy zauważyć, że spełniony jest pierwszy warunek równości funkcji.
.
Sprawdzimy, czy spełniony jest warunek drugi. W tym celu przekształcimy tożsamościowo wzory opisujące obie funkcje.
, gdy
, gdy
Aby wykazać, że funkcje i nie są równe wystarczy znaleźć jeden argument, dla którego wartości funkcji są różne. Np. .
,
.
Zatem funkcje i nie są równe.
Ad. b). Wyznaczymy dziedziny obu funkcji.
Dziedzina funkcji .
Mianownik ułamka musi być liczbą różną od zera.
Zatem .
Dziedzina funkcji .
Funkcja przyjmuje wartość dla .
Zatem .
Dziedziny obu funkcji są różne, czyli nie spełniony jest warunek pierwszy.
Funkcje i nie są równe.
Funkcje są równe wtedy, gdy mają takie same dziedziny i dla każdego argumentu należącego do tej dziedziny wartości funkcji są równe.
Funkcje nie są równe wtedy gdy mają różne dziedziny lub dla co najmniej jednego argumentu należącego do dziedziny mają różne wartości.
Słownik
funkcje, które mają taką samą dziedzinę i dla każdego argumentu należącego do tej dziedziny wartości funkcji są równe