Przeczytaj

Podstawowe pojęcia

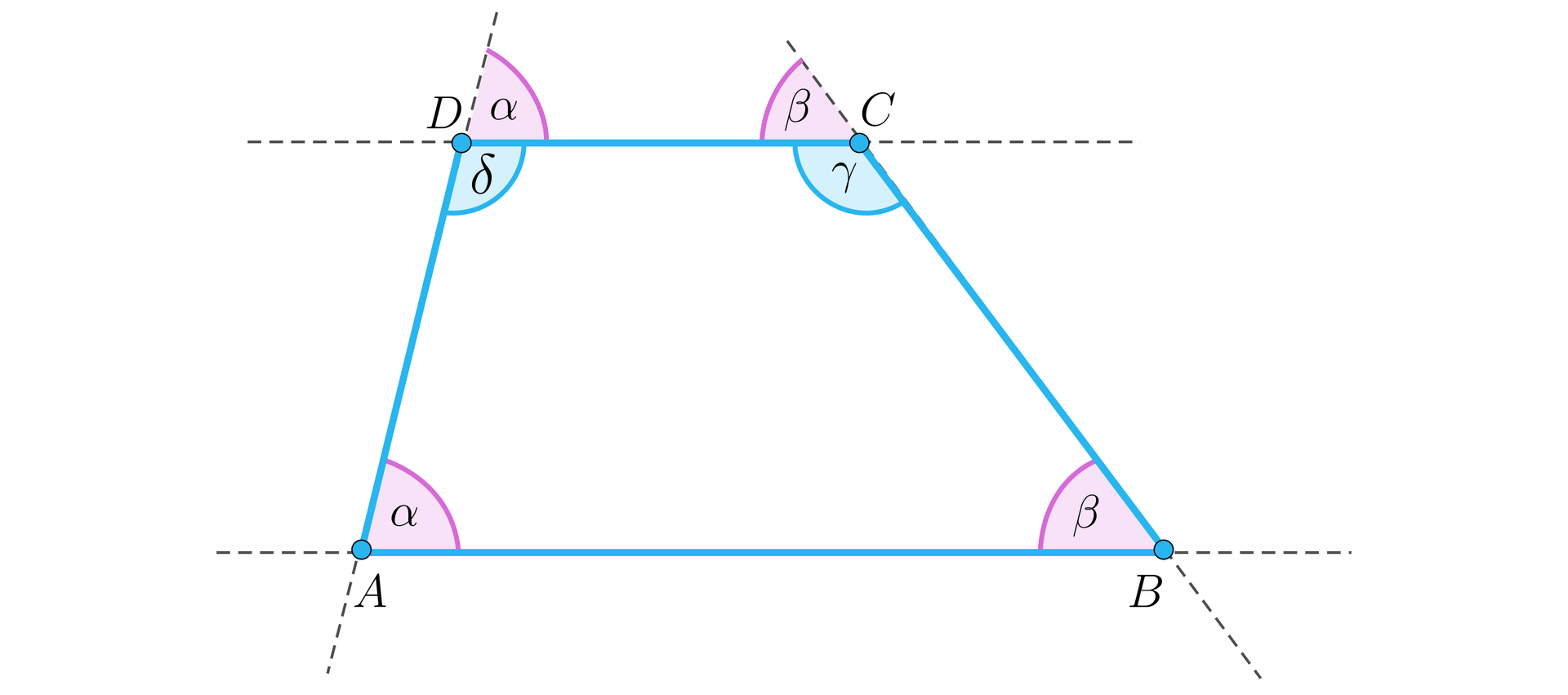
Na rysunku przedstawiony jest czworokąt $A B C D$ z zaznaczonymi kątami.

R18jPSuRs6Rg2

Ilustracja przedstawia czworokąt ABCD z zaznaczonymi kątami. Kąt alfa przy wierzchołku A, kąt beta przy wierzchołku B, kąt gamma przy wierzchołku C oraz kąt delta przy wierzchołku D.

Odcinki $A B$ , $B C$ , $C D$ , $D A$ nazywamy bokami czworokąta $A B C D$ . Dla uproszczenia oznaczamy je małymi literami $a$ , $b$ , $c$ , $d$ . Litery te są stosowane zarówno do nazywania boków jak i do zapisania długości boków.

Punkty $A$ , $B$ , $C$ , $D$ są wierzchołkami czworokąta. Jeśli wierzchołki leżą na jednym boku, to mówimy, że są sąsiednie a w przeciwnym przypadku – są przeciwległe.

Odcinek łączący dwa przeciwległe wierzchołki nazywamy przekątną.

Stąd wynika od razu, że czworokąt ma dwie przekątne.

Boki, które mają wspólny wierzchołek, nazywamy bokami sąsiednimi a w przeciwnym przypadku – przeciwległymi.

Kąty $α$ , $β$ , $γ$ , $δ$ nazywamy kątami wewnętrznymi (lub krócej kątami) czworokąta.

Jeśli dwa kąty mają wspólne ramię (bok czworokąta) to są kątami sąsiednimi a w przeciwnym przypadku – przeciwległymi.

Suma kątów czworokąta wynosi $360 °$ .

Podział ze względu na wypukłość kątów

Figurą wypukłą nazywamy taką figurę, dla której odcinek łączący dowolne dwa punkty należące do tej figury jest zawarty w tej figurze.

Kąt jest wypukły jeśli ma miarę mniejszą lub równą $180 °$ . W czworokątach wewnętrzny kąt wypukłykąt wypukłykąt wypukły ma miarę mniejszą niż $180 °$ .

Kąt, który ma miarę większą niż $180 °$ nazywany jest kątem wklęsłym.

Przykład 1

Pokażemy, że kąt wklęsłykąt wklęsłykąt wklęsły nie jest wypukły.

Rozwiązanie

Przeanalizujmy rysunek.

R1AxuQbwtCHvP

Ilustracja przedstawia kąt wklęsły o mierze alfa większej, niż 180 stopni. Kąt wyznaczają dwie półproste o wspólnym wierzchołku, które dzielą płaszczyzną na dwie części: pierwsza część to ta, w której wykreślono kąt alfa, a druga część płaszczyzny to ta, w której ramiona wyznaczają dopełnienie kąta alfa do kąta pełnego. Ramiona kąta alfa przecina odcinek AB. Punkty przecięcia z ramionami kąta to punkty D i E.

Punkty $A$ i $B$ należą do kąta $α$ . Natomiast odcinek $A B$ w części $D E$ nie leży w obrębie tego kąta, a to znaczy, że ten kąt nie jest wypukły.

czworokąt wklęsły i wypukły

Definicja: czworokąt wklęsły i wypukły

Czworokąt jest wypukłyczworokąt wypukłyCzworokąt jest wypukły jeśli jest figurą wypukłą. Czworokąt, jest wklęsłyczworokąt wklęsłyCzworokąt, jest wklęsły jeśli nie jest figurą wypukłą.

charakteryzacja wypukłości

Własność: charakteryzacja wypukłości

Czworokąt jest wypukły wtedy i tylko wtedy, gdy jego wszystkie cztery kąty wewnętrzne są wypukłe. Czworokąt jest wklęsły wtedy i tylko wtedy, gdy dokładnie jeden z jego kątów wewnętrznych jest wklęsły.
Przekątne w czworokącie wypukłym zawierają się w tym czworokącie, natomiast w czworokącie wklęsłym jedna przekątna leży poza czworokątem.

Zauważmy, że czworokąt może mieć tylko jeden kąt wklęsły, bo gdyby miał dwa takie kąty, to suma ich miar byłaby większa od $360 °$ a to nie jest możliwe, gdyż suma wszystkich kątów czworokąta jest równa $360 °$ .

Na rysunku poniżej czworokąt niebieski jest wypukły, a zielony jest wklęsły. Przekątne narysowane są linią przerywaną. Widać, że przekątna $E G$ w czworokącie zielonym leży poza tym czworokątem, więc przekątne nie przecinają się.

R16dQWEjulXms

Ilustracja przedstawia dwa czworokąty. Czworokąt A B C D znajdujący się po lewej stronie jest wypukłym deltoidem. Jego przekątne A C oraz B D znajdują się wewnątrz figury. Czworokąt E F G H znajdujący się po prawej stronie jest wklęsły i ma kształt grota strzałki. Jego przekątna F H znajduje się wewnątrz figury, natomiast jego przekątna E G leży poza wnętrzem figury.

W czworokącie wypukłym przekątne się przecinają.

Otrzymaliśmy więc pierwszy podział czworokątów na wypukłe i wklęsłe.

R1WMd6Cd8QMaQ

Ilustracja przedstawia czworokąt wypukły z wewnętrznymi kątami nie przekraczającymi miary 180 stopni, którego przekątne znajdują się we wnętrzu figury oraz czworokąt wklęsły posiadający trzy ostre kąty wewnętrze oraz jeden kąt wewnętrzy o mierze większej, niż 180 stopni. Figura ma kształt grota strzałki. Jedna z przekątnych czworokąta znajduje się wewnątrz figury, a druga poza nią.

Podział ze względu na równoległość boków

Trapezem nazywamy czworokąt, który ma przynajmniej jedną parę boków równoległych.

Boki równoległe nazywamy podstawami, a pozostałe dwa boki – ramionami.

charakteryzacja trapezów

Własność: charakteryzacja trapezów

Suma kątów przy ramieniu trapezu jest równa $180 °$ .
Jeżeli w czworokącie suma kątów przy jednym z boków jest równa $180 °$ , to ten czworokąt jest trapezem.
Jeśli czworokąt jest trapezem, to jest wypukły.

Dowód

Własności $1$ . i $2$ . wynikają z twierdzenia o prostych równoległych przeciętych trzecią prostą. Własności $1$ . i $2$ . wykluczają sytuację, w której jeden z kątów miałby miarę większą od $180 °$ , więc trapeztrapeztrapez jest czworokątem wypukłym.

RhTwTb0SIyif2

Ilustracja przedstawia czworokąt ABCD. Kąty przy wierzchołkach wynoszą kolejno, przy wierzchołku A alfa, przy wierzchołku B beta, przy wierzchołku C gamma oraz przy wierzchołku D delta. Kąty poza czworokątem przy wierzchołku C wynoszą beta, a przy wierzchołku D alfa.

Przykład 2

Na rysunku przedstawione są czworokąty z zaznaczonymi kątami. Pokażemy, które z nich są trapezami, a które nie są.

R1HT6oHRt6m7r

Ilustracja przedstawia sześć czworokątów. Pierwszy niebieski ABCD jest trapezem prostokątnym o kątach prostych przy wierzchołkach B i C. Drugi niebieski EFGH jest równoległobokiem o kątach wewnętrznych wynoszących 116,6° oraz 63,4°. Trzeci niebieski trapez IJKL posiada kąty wewnętrzne 120 stopni oraz 60 stopni. Czwarty różowy czworokąt MNOP posiada kąty wewnętrzne wynoszące 121 stopni 52 przecinek 1 stopnia oraz 37 przecinek 9 stopnia. Piąty różowy czworokąt RSTQ jest czworokątem wypukłym w kształcie grota strzałki. A szósty różowy deltoid UVWZ ma kąty wewnętrzne równe 116 przecinek 6 przy wierzchołkach V i Z oraz 36 przecinek 9 przy wierzchołku W.

Rozwiązanie

Czworokąty niebieskie są trapezami, bo suma miar dwóch sąsiednich kątów jest równa $180 °$ .

Czworokąty różowe nie są trapezami, bo jeden z nich jest wklęsły a w pozostałych dwóch suma miar żadnych dwóch sąsiednich kątów nie jest równa $180 °$ .

o przekątnych trapezu

Twierdzenie: o przekątnych trapezu

Punkt $P$ przecięcia przekątnych trapezu $A B C D$ , w którym $A B ∥ C D$ dzieli przekątne w stosunku $|A B| : |C D|$ , czyli przy oznaczeniach z rysunku $|A P| : |C P| = |A B| : |C D|$ .

RIfNeIQnoOEqu

Ilustracja przedstawia trapez ABCD z przekątnymi przecinającymi się w punkcie P.

Dowód tego twierdzenia wynika wprost z odwrotnego twierdzenia Talesa.

Trapez o równych ramionach nazywany jest trapezem równoramiennym.

trapezów równoramiennych

Własność: trapezów równoramiennych

W trapezie równoramiennym o różnych podstawach kąty przy podstawach są równe. Ponadto, kąt przy dłuższej podstawie jest ostry, a kąt przy krótszej podstawie jest rozwarty.
Jeśli przekątne w trapezie są równej długości, to jest on trapezem równoramiennym.

Dowód

Skorzystamy z rysunku. Jeśli trapez ma podstawy różnej długości, to jego ramiona można przedłużyć do punktu $O$ tak, by powstał trójkąt $D C O$ , w którym $A B ∥ C D$ . Z twierdzenia Talesa wynika, że jeśli $|A D| = |B C|$ , to trójkąt $D C O$ jest równoramienny, więc kąty przy wierzchołku $D$ i $C$ są równe. Stąd kąty trapezu przy wierzchołkach $A$ i $B$ są równe jako kąty przyległe do kąta $β$ . To dowodzi własności $1$ .

R2KFBEbzphLNE

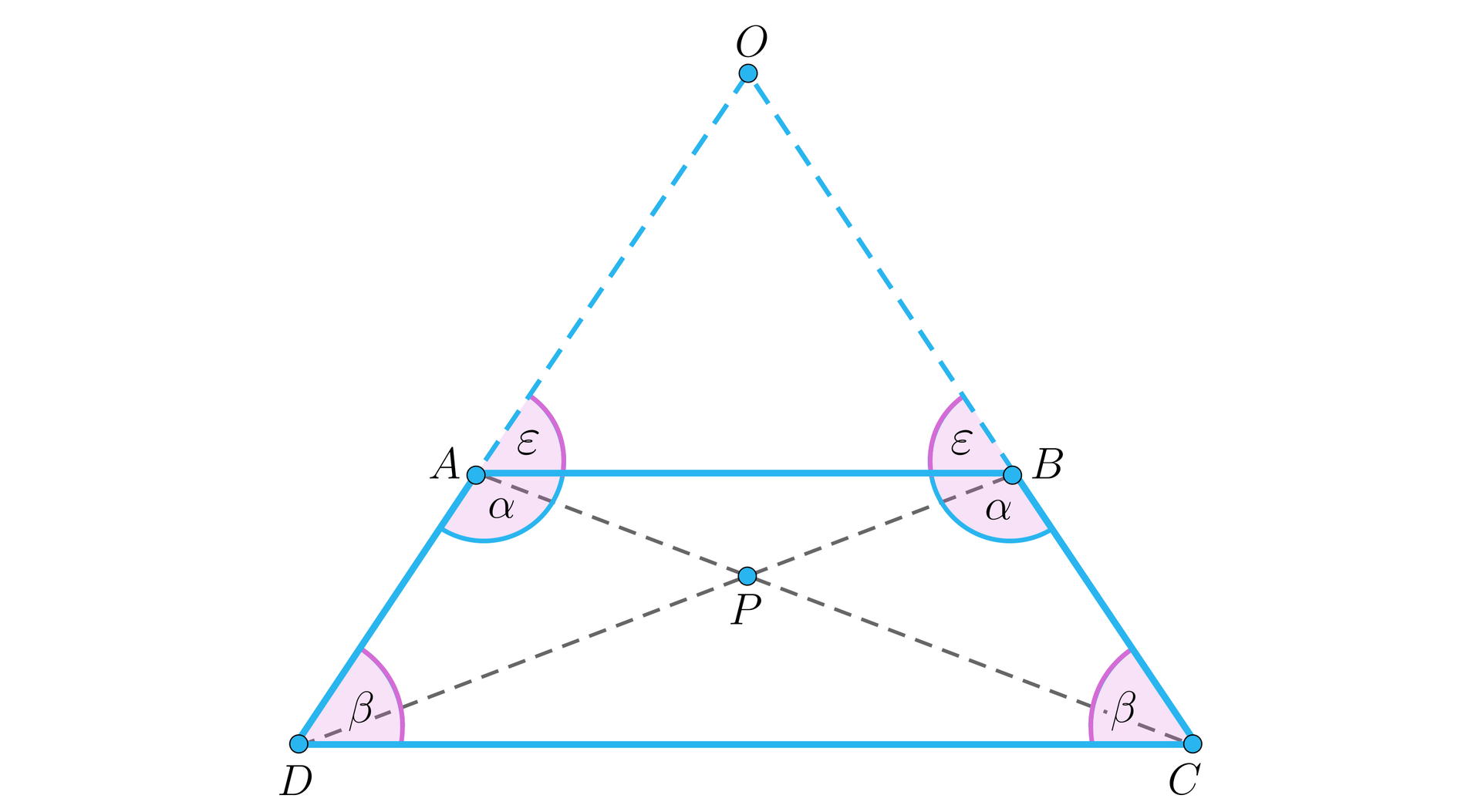
Ilustracja przedstawia trapez ABCD z przekątnymi przecinającymi się w punkcie P. Kąt przy wierzchołku A i B ma miarę alfa, a przy wierzchołku D i C ma miarę beta. Przedłużono ramiona AD i BC tworząc trójkąt ABO. Kąty wewnętrzne tego trójkąta przy podstawie wynoszą epsilon.

Aby pokazać własność $2$ ., załóżmy, że przekątne $A C$ i $B D$ są równej długości. Stąd i z twierdzenia o przekątnych trapezu wynika, że $|D P| = |C P|$ oraz $|A P| = |B P|$ . Poza tym trójkąty $A P D$ i $B P C$ mają równe kąty przy wierzchołku $P$ jako kąty wierzchołkowe.

Z cechy przystawanie trójkątów $b - k - b$ trójkąty $A P D$ i $B P C$ są przystające i stąd $|A D| = |B C|$ .

Przykład 3

Pokażemy, że jeśli w trapezie kąty przy podstawie są równe, to trapez jest równoramienny.

Rozwiązanie

Jeśli kąty przy podstawie są kątami prostymi, to trapez jest prostokątem, czyli jest równoramienny. W przeciwnym przypadku przedłużenia ramion przecinają się tworząc trójkąt równoramienny. Druga podstawa trapezu ma wierzchołki na ramionach kąta, który tworzą przedłużenia ramion trapezu. Z równoległości podstaw trapezu i z twierdzenia Talesa wynika, że trapez jest równoramiennytrapez równoramiennytrapez jest równoramienny.

Klasycznie równoległobokrównoległobokrównoległobok definiuje się jako czworokąt, który ma dwie pary boków równoległych. Stąd wynika, że równoległobok jest trapezem.

Spróbujmy jednak scharakteryzować trapez, w którym podstawy są równej długości.

charakteryzacja równoległoboków

Własność: charakteryzacja równoległoboków

Trapez, którego podstawy są równe, jest równoległobokiem.
Równoległobok jest trapezem równoramiennym.
Przekątne równoległoboku przecinają się w połowie.
Jeśli przekątne czworokąta przecinają się w połowie, to czworokąt jest równoległobokiem.
Suma sąsiednich kątów w równoległoboku jest równa $180 °$ , a kąty przeciwległe są równe.

Dowód

Na rysunku odcinki $A B$ i $C D$ mają równe długości. Linie przerywane przedstawiają proste przechodzące przez punkty $A$ , $D$ i $B$ , $C$ , odpowiednio. Proste te są równoległe, bo w przeciwnym przypadku miałyby punkt przecięcia $O$ i wtedy twierdzenie Talesa przeczyłoby równości podstaw $A B$ i $C D$ .

RQhy59GKfY5jd

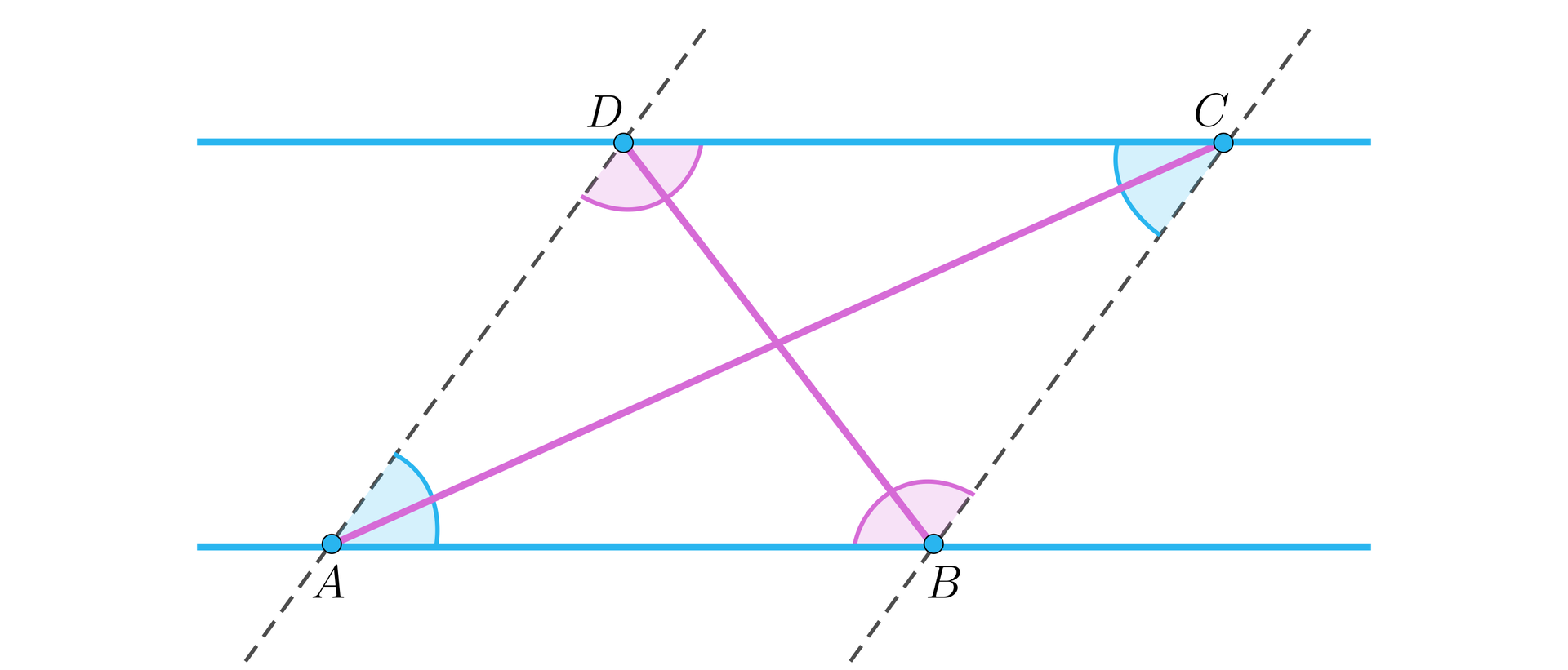
Ilustracja przedstawia równoległobok ABCD osadzony na dwóch równoległych prostych. Czworokąt posiada przekątne przecinające się, znajdujące się wewnątrz figury. Czworokąt posiada dwie pary równych kątów leżących naprzeciw siebie: A i C oraz B i D.

To dowodzi własności $1$ . oraz $2$ .

Własności $3$ . i $4$ . wynikają z twierdzenia o przekątnych w trapezie i z twierdzenia Talesa.

Natomiast własność $5$ . wynika z faktu, że ramiona równoległoboku są zarówno podstawami jak i ramionami, a suma kątów przy ramionach trapezu jest równa
$180 °$ .

Przykład 4

Pokażemy, że przekątna równoległoboku dzieli równoległobok na dwa trójkąty przystające.

Rozwiązanie

Weźmy dowolną przekątną równoległoboku, na przykład $A C$ na rysunku.

R4B51gE2lGX4S

Wtedy odpowiednie boki w trójkątach $A D C$ i $A B C$ są równe, więc na mocy cechy przystawania $b - b - b$ trójkąty te są przystające.

Otrzymaliśmy więc podział czworokątów wypukłych jak na rysunku.

RmR5hUnRDI4zS

Ilustracja przedstawia podział czworokątów. W zbiorze czworokątów wypukłych znajduję się zbiór trapezów, w zbiorze trapezów można znaleźć trapezy równoramienne, a w zbiorze trapezów równoramiennych można znaleźć zbiór równoległoboków.

Podział ze względu na kąt prosty

Z faktu, że w czworokącie jest jeden kąt prosty, nie wynika jakaś szczególna własność. Taki czworokąt może być zarówno wypukły jak i wklęsły. Zatem do klasyfikacji potrzeba jeszcze dodatkowych warunków.

Jeśli zapytamy o czworokąty, w których są dwa kąty proste, to wykluczymy czworokąty wklęsłe, bo suma dwóch pozostałych kątów jest wtedy równa $180 °$ .

Jeśli czworokąt ma dwa przeciwległe kąty proste, to możemy tylko powiedzieć, że jest wypukły.

Jeśli natomiast ma dwa sąsiednie kąty proste, to jest trapezem jak pokażemy w dowodzie własności prostokątaprostokątprostokąta.

Trapez, w którym kąt przy podstawie jest prosty, nazywamy trapezem prostokątnym.

Wprost z własności kątów trapezu wynika, że trapez prostokątny ma dwa kąty proste przy ramieniu.

Przykład 5

Na rysunku przedstawiono czworokąty, które mają przynajmniej jeden kąt prosty. Określimy rodzaj podanych czworokątów.

RA7Fjtbe7qZEE

Ilustracja przedstawia pięć czworokątów. Pierwszy różowy o kątach wewnętrznych równych 83 stopnie, 80 przecinek 4 stopnia, 106 przecinek 6 stopnia oraz 90 stopni. Drugi różowy w kształcie grota strzałki o kącie wklęsłym, prostym oraz dwoma ostrymi. Trzeci zielony o dwóch kątach prostych oraz jednym o mierze 76 stopni. Czwarty niebieski o dwóch kątach prostych oraz jednym o mierze 116 przecinek 6 stopnia. Piąty niebieski o dwóch kątach prostych.

Rozwiązanie

Czworokąty różowe mają jeden kąt prosty. Jeden z nich jest wypukły (po lewej) a drugi jest wklęsły. Nie mają żadnych dodatkowych cech charakterystycznych.

Czworokąt zielony ma przeciwległe kąty proste. Jest wypukły i nie ma żadnych dodatkowych cech charakterystycznych.

Czworokąty niebieskie mają dwa kąty sąsiednie proste. Są trapezami prostokątnymi.

Prostokąt to czworokąt, który ma wszystkie kąty proste.

charakteryzacja prostokątów

Własność: charakteryzacja prostokątów

Prostokąt jest trapezem prostokątnym.
Prostokąt jest równoległobokiem.
Jeżeli w trapezie kąty przy podstawie są proste, to ten trapez jest prostokątem.
Jeżeli w równoległoboku jeden z kątów jest prosty, to jest on prostokątem.

Dowód

Skorzystamy z oznaczeń na rysunku

RsdcmbTBL2toL

Ilustracja przedstawia czworokąt ABCD usadzony na dwóch prostych. Jego przekątne przecinają się, a kąty wewnętrzne maja 90 stopni.

Załóżmy, że w czworokącie kąty przy wierzchołkach $A$ i $B$ są proste. Wtedy boki $A D$ i $B C$ są równoległe, więc czworokąt ten jest trapezem prostokątnym. Z definicji prostokąta wynika też, że kąt przy wierzchołku $C$ jest prosty i stąd $C D ∥ A B$ . Zatem prostokąt jest równoległobokiem. Pokazaliśmy więc własności $1$ .
i $2$ .

Jeżeli kąty przy podstawie $A B$ trapezu $A B C D$ są proste, to $A D$ i $B C$ są prostopadłe do $A B$ oraz $A D ∥ B C$ , ale $C D$ jest równoległa do $A B$ , więc $A D$ i $B C$ są prostopadłe do $C D$ . Stąd $A B C D$ jest prostokątem.

Załóżmy, że w równoległoboku $A B C D$ kąt przy wierzchołku $A$ jest prosty. Wtedy kąt przeciwległy do niego ma tę samą miarę, więc też jest prosty. Natomiast miary kątów sąsiednich do tego kąta sumują się z nim do $180 °$ , więc kąty sąsiednie są proste. Pokazaliśmy więc, że równoległobok $A B C D$ jest prostokątem.

Wprost z faktu, że prostokąt jest równoległobokiem, wynika, że przeciwległe boki prostokąta są równe i że przekątne prostokąta dzielą się w połowie.

Przykład 6

Na rysunku przedstawiona jest litera $N$ . Pokażemy, z jakich rozłącznych czworokątów można zbudować tę literę.

RDHp3UBaAffV4

Ilustracja przedstawia literę N zbudowaną z kwadratów i osadzoną na tle w kratkę. Pionowa lewa kreska litery ma wymiary dwa w poziomie na pięć w pionie, tak samo prawa pionowa kreska. Cała litera ma łącznie wymiary 6 w poziomie na 5 w pionie.

Rozwiązanie

Podział wzdłuż zaznaczonych odcinków wskazuje dwa prostokąty i jeden równoległobok.

RqIJa8JhhrMzn

Ilustracja przedstawia literę N zbudowaną z czworokątów. Pionowe linie dzielą je na następujące figury. Dwóch prostokątów oraz jednego równoległoboku.

Ten rysunek przedstawia podział na równoległobok i dwa trapezy.

RfRhZB3mjmBqx

Ilustracja przedstawia literę N zbudowaną z czworokątów. Ukośne linie dzielą literę na figury .Dwóch trapezów prostokątnych oraz równoległoboku.

Kolejna linia dzieli literę na dwa trapezy i dwa prostokąty.

R1R5gdSellKRN

Ilustracja przedstawia literę N zbudowaną z czworokątów. Pozioma linia dzieli ją na dwie figury, dwa trapezy prostokątne oraz dwa kwadraty

Otrzymaliśmy więc podział trapezów jak na rysunku.

RVBfrI1qHxJVq

Ilustracja przedstawia podział trapezów. W zbiorze trapezów znajdują się dwa podzbiory połączone ze sobą, są to trapezy prostokątne oraz trapezy równoramienne. Do trapezów równoramiennych należą równoległoboki. Najmniejszym podzbiorem należącym do każdego rodzaju trapezów są prostokąty.

Podział ze względu na równość boków

Kolejną cechą pozwalającą rozróżniać czworokąty jest równość boków.

Jeżeli czworokąt ma dwie pary równych boków przeciwległych, to jest on równoległobokiem.

Jeśli czworokąt ma dwie pary równych boków sąsiednich, to dostaniemy czworokąt deltoidalnyczworokąt deltoidalnyczworokąt deltoidalny, a jeśli dodatkowo założymy, że jest wypukły, to dostaniemy deltoid.

Ostatecznie, jeśli czworokąt ma wszystkie boki równe, to jest rombemrombrombem.

Kwadrat definiuje się jako czworokąt, który ma wszystkie boki równe i wszystkie kąty proste.

Zatem kwadratkwadratkwadrat jest prostokątem, który ma wszystkie boki równe i jednocześnie jest rombem, który ma wszystkie kąty równe.

Przykład 7

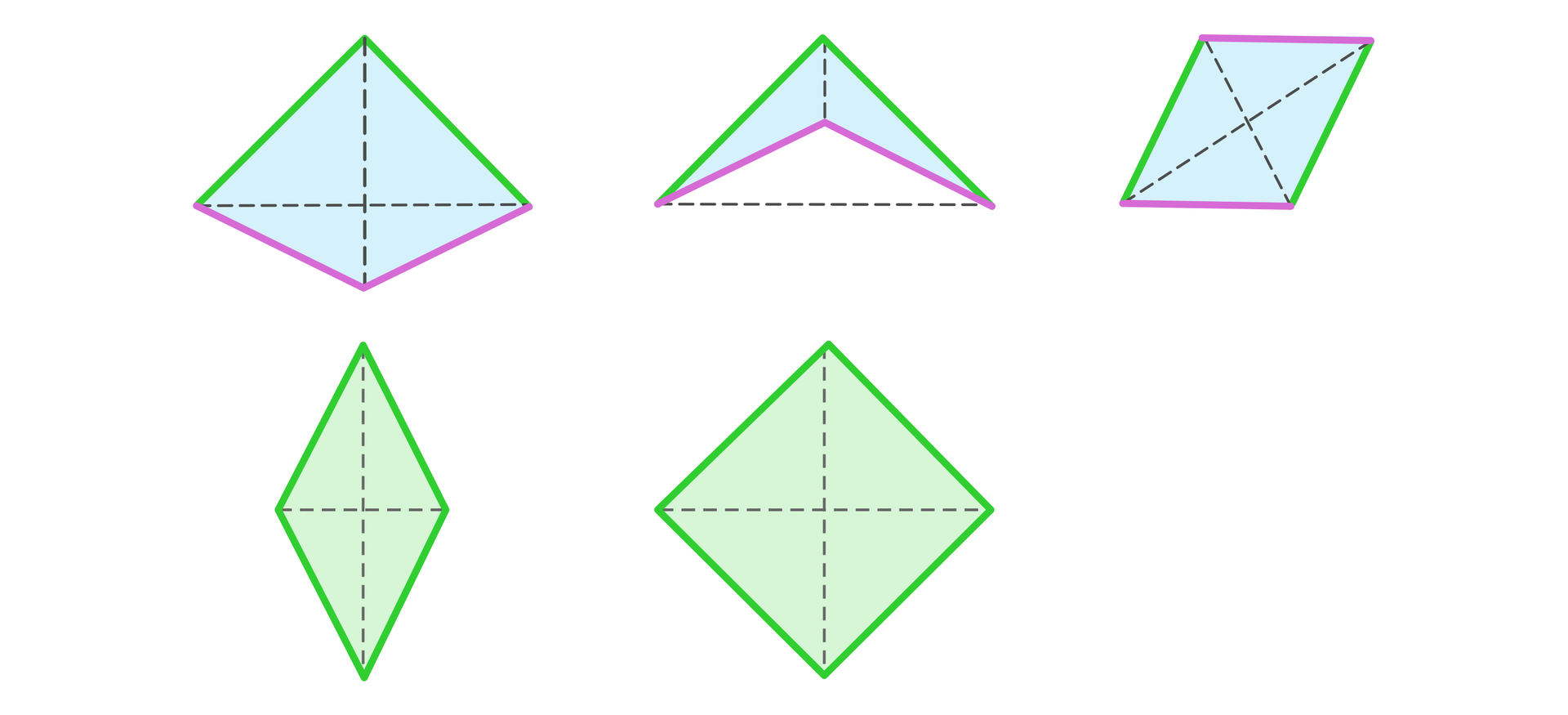
Na rysunku równe boki oznaczone są tym samym kolorem. Określimy rodzaje narysowanych czworokątów.

RzDePEX2oWDh6

Ilustracja przedstawia pięć czworokątów. Pierwszy jest niebieskim czworokątem z dwoma parami równych boków. Jest to pionowo ustawiony deltoid, w którym górne boki są równe i dolne boki są równe. Przekątne figury przecinają się i znajdują się w jej wnętrzu. Drugi jest niebieskim czworokątem wklęsłym w kształcie grotu strzałki wskazującej w górę posiadającym dwie pary równych boków . Dwa górne boki są równe i dwa dolne boki są równe. Jedna z przekątnych figury znajduje się wewnątrz, a druga na zewnątrz czworokąta, przekątne nie przecinają się. Trzeci jest niebieskim równoległobokiem i posiada dwie pary równych równoległych boków. Prawy i lewy bok są równe oraz górny i dolny bok są równe. Przekątne figury znajdują się w jej wnętrzu i przecinają się. Czwarty jest zielonym deltoidem o wszystkich bokach równych, którego przekątne przecinają się i znajdują się w jego wnętrzu, a piąty zielonym kwadratem, którego przekątne również przecinają się i znajdują w jego wnętrzu.

Rozwiązanie

Niebieskie figury to od lewej: deltoiddeltoiddeltoid, bo jest wypukły i ma dwie pary równych boków sąsiednich; kolejny jest czworokątem deltoidalnym, bo jest wklęsły i ma dwie pary równych boków sąsiednich; trzeci z nich jest równoległobokiem, bo ma równe dwie pary przeciwległych boków. Figury zielone to romby, bo mają wszystkie boki równe, a romb po prawej jest kwadratem.

Na rysunku w powyższym przykładzie zaznaczono również przekątne. Zauważmy, że w deltoidzie i dwóch rombach przekątne przecinają się pod kątem prostym.

przekątnych w deltoidzie

Własność: przekątnych w deltoidzie

Przekątne deltoidu przecinają się pod kątem prostym i jedna z przekątnych dzieli drugą na połowy.
Jeśli przekątne czworokąta przecinają się pod kątem prostym i jedna z przekątnych dzieli drugą na połowy, to jest on deltoidem.
Przekątne rombu przecinają w połowie i pod kątem prostym.

Dowód

Niech czworokąt $A B C D$ będzie deltoidem, przy czym $|B A| = |B C|$ i
$|D A| = |D C|$ .

R1HGdKpqWtxlD

Ilustracja przedstawia deltoid ABCD z przekątnymi przecinającymi się w punkcie F. Pary boków AB i BC oraz AD i CD są równe.

Poprowadźmy symetralną przekątnej $A C$ . Symetralna odcinka jest zbiorem punktów równoodległych od końców tego odcinka. Stąd wynika, że wierzchołki $B$ i $D$ leżą na symetralnej, więc przekątna $A C$ przecina przekątną $B D$ pod kątem prostym. W ten sposób pokazaliśmy własność $1$ .

Do dowodu własności $2$ również wykorzystamy symetralną. Jeśli przekątne czworokąta $A B C D$ przecinają się pod kątem prostym i przekątna $B D$ dzieli $A C$ na połowy. Wtedy czworokąt jest wypukły i BD leży na symetralnej odcinka $A C$ .

Stąd $|B A| = |B C|$ i $|D A| = |D C|$ , więc czworokąt $A B C D$ jest deltoidem.

Ponieważ romb jest deltoidem, to przekątne przecinają się pod kątem prostym. A ponieważ jest również równoległobokiem, to przekątne dzielą się w połowie.

Przekątne kwadratu są prostopadle do siebie i dzielą się w połowie, bo kwadrat jest rombem.

Otrzymaliśmy więc podział czworokątów jak na rysunku.

RLWHsphUVdeZA

Ilustracja przedstawia zbiór czworokątów wypukłych. Należą do nich podzbiory powiązane ze sobą deltoidy i równoległoboki. Do równoległoboków należą prostokąty i romby. Do prostokątów należą kwadraty.

Ostateczna klasyfikacja czworokątów wygląda następująco:

RNKcfnagnfiHs

Ilustracja przedstawia zbiór czworokątów. Składa się kolejno z podzbiorów czworokąty wypukłe, w środku których znajdują się trapezy, w środku których znajdują się trapezy równoramienne, w środku których znajdują się równoległoboki, w środku których znajdują się prostokąty. W prostokątach znajduje się zbiór deltoidalnych, w skład których wchodzą deltoidy romby oraz kwadraty.

Słownik

kąt wypukły

kąt, który ma miarę mniejszą lub równą $180 °$

kąt wklęsły

kąt, który ma miarę większą niż $180 °$

czworokąt wypukły

czworokąt, którego wszystkie cztery kąty wewnętrzne są wypukłe

czworokąt wklęsły

czworokąt, którego jeden z kątów wewnętrznych jest wklęsły

trapez

czworokąt, który ma przynajmniej jedną parę boków równoległych

trapez równoramienny

trapez, którego ramiona mają równe długości

równoległobok

czworokąt, który ma dwie pary boków równoległych

prostokąt

czworokąt, który ma wszystkie kąty proste

kwadrat

czworokąt, który ma wszystkie boki równe i wszystkie kąty proste

romb

czworokąt, który ma wszystkie boki równe

deltoid

czworokąt wypukły, który ma dwie pary równych boków sąsiednich

czworokąt deltoidalny

czworokąt, który ma dwie pary równych boków sąsiednich

Wprowadzenie

Infografika

Podstawowe pojęcia

Podział ze względu na wypukłość kątów

Podział ze względu na równoległość boków

Podział ze względu na kąt prosty

Podział ze względu na równość boków

Słownik