Liczba chromatyczna

Kolorowanie wierzchołków grafu polega na przypisaniu każdemu wierzchołkowi pewnej liczby naturalnej (dopuszczlne są również litery). Kolorowanie uznajemy za poprawne, jeśli żadna para wierzchołków sąsiednich nie jest pokolorowana tym samym kolorem. Przypisanie kolorów wierzchołkom grafu możemy przeprowadzić na wiele sposobów.

Graf k-kolorowy to graf, który można pokolorować k kolorami.

Dla każdego grafu można wyznaczyć minimalną liczbę kolorów użyta do kolorowania grafu. Liczbę tę nazywamy liczbą chromatycznąliczba chromatycznaliczbą chromatyczną grafu.

Znajdowanie najmniejszej liczby kolorów do pokolorowania wierzchołków jest problemem NP‑trudnymproblem NP‑trudnyNP‑trudnym.

Znamy już jedną z metod kolorowania grafu wykorzystującą podejście zachłanne. Polega ona na tym, że algorytm iteruje po każdym wierzchołku grafu, przypisując mu pierwszy dostępny kolor, jeszcze niewykorzystany przez sąsiadów. Niestety, o ile algorytm zachłanny dokonuje poprawnego kolorowania wierzchołków, o tyle sposób przypisania im kolorów nie zawsze jest optymalny. W konsekwencji wyznaczenie dokładnej wartości liczby chromatycznej grafu metodą zachłanną zwykle jest niemożliwe.

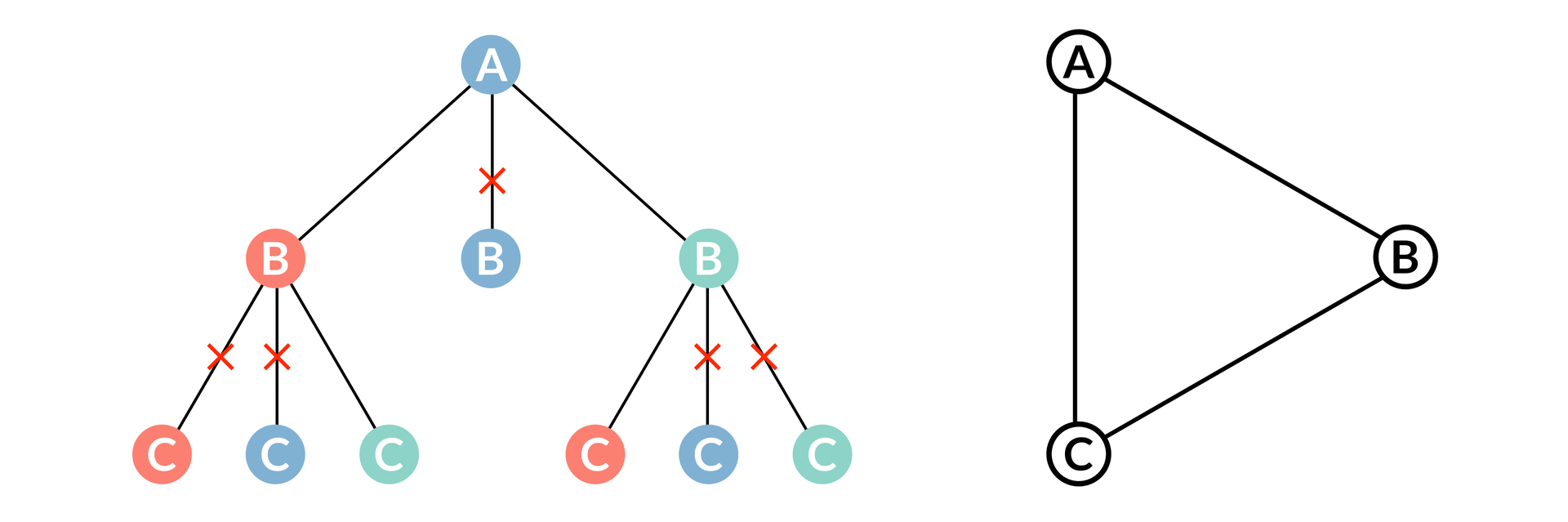
Istnieje jednak metoda kolorowania wierzchołków grafu, która wykorzystuje w swoim działaniu algorytm z nawrotami. Polega to na testowaniu wszystkich konfiguracji przypisania kolorów wierzchołkom oraz wybrania tej, która składa się z najmniejszej liczby kolorów. Przy każdym kroku budowania rozwiązania sprawdzane jest, czy obecne rozwiązanie wygeneruje dobre pokolorowanie albo czy nie przekracza określonej liczby kolorów.

Na powyższym rysunku po prawej stronie znajduje się graf złożony z trzech wierzchołków, który chcemy pokolorować. Po lewej stronie przedstawione jest drzewo z kolejnymi krokami kolorowania grafu przy użyciu algorytmu z nawrotami. Podążając nieprzekreślonymi krawędziami, znajdziemy poprawnie pokolorowany graf.

Poniżej znajduje się specyfikacja oraz pseudokod omówionego tu algorytmu kolorowania wierzchołków grafu.

Specyfikacja problemu:

Dane:

• V - liczba całkowita; liczba wierzchołków grafu

• macierz_sąs - macierz sąsiedztwa grafu

Wynik:

• kolory[1..V] - tablica liczb całkowitych; wyznaczone optymalne kolorowanie grafu

Pseudokod:

funkcja kolizje(wierzchołek, kolory, macierz_sąs)
	dla i = 1, 2, ..., długość(macierz_sąs) wykonuj:
		jeżeli i != wierzchołek ORAZ macierz_sąs[wierzchołek][i] > 0 I kolory[i] = kolory[wierzchołek]:
			zwróć prawda
	zwróć fałsz


V ← liczba wierzchołków grafu; liczba całkowita
macierz_sąs ← macierz sąsiedztwa grafu
kolory[1..V] ← tablica wypełniona zerami (0 oznacza brak koloru)
dla liczba_kolorów = 1, 2, ..., V wykonuj:
	wierzchołek = 1
	dopóki wierzchołek > 0 wykonuj:
		czy_koliduje ← prawda
		dopóki czy_koliduje = prawda ORAZ kolory[wierzchołek] < liczba_kolorów wykonuj:
			kolory[wierzchołek] ← kolory[wierzchołek] + 1
			czy_koliduje ← kolizje(wierzchołek, kolory, macierz_sąs)
		jeżeli czy_koliduje = fałsz:
			jeżeli wierzchołek = V:
				wyświetl kolory
				zakończ
			w przeciwnym wypadku:
				wierzchołek ← wierzchołek + 1
		w przeciwnym wypadku:
			kolory[wierzchołek] ← 0
			wierzchołek ← wierzchołek - 1

Indeks chromatyczny

Kolorowanie grafu można również rozumieć jako przypisywanie kolorów krawędziom. Aby kolorowanie krawędzi zostało uznane za poprawne, każda para krawędzi wychodząca z wierzchołka musi mieć przypisany inny kolor. Jeśli do pokolorowania krawędzi grafu użyto najmniejszej możliwej liczby kolorów, to takie kolorowanie krawędzi uznajemy za optymalne. Najmniejszą liczbą kolorów potrzebną do pokolorowania krawędzi grafu nazywamy indeksem chromatycznymindeks chromatycznyindeksem chromatycznym grafu.

Grafy planarne

Graf planarnygraf planarnyGraf planarny to graf, który można narysować na płaszczyźnie w taki sposób, aby żadne dwie krawędzie nie przecinały się ze sobą.

Tego rodzaju grafy mogą służyć do reprezentacji mapy podziałów terytorialnych. Dla przykładu załóżmy, że za pomocą grafu chcemy przedstawić mapę administracyjną Polski. Każde województwo będzie reprezentowane przez wierzchołek grafu. Z kolei krawędzie połączą dwa wierzchołki odpowiadające sąsiednim województwom.

Planarność grafu jest blisko związania z kolorowaniem grafu oraz liczbą chromatyczną. Jedno z popularniejszych twierdzeń matematycznych — twierdzenie o czterech barwach — określa liczbę kolorów, których zawsze można użyć dla pokolorowania grafu planarnego.

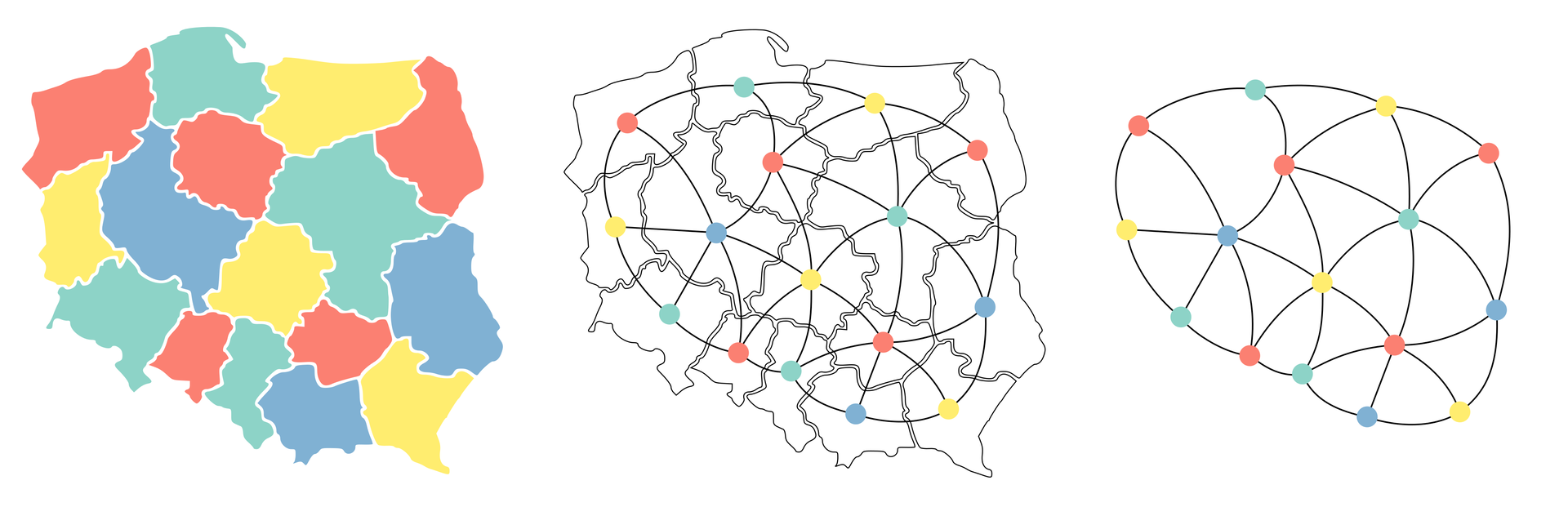
Teza twierdzenia o czterech barwach początkowo została zaproponowana w kontekście kolorowania mapy. Pomimo prostego sformułowania twierdzenie było bardzo trudne do udowodnienia. Po raz pierwszy jego prawdziwość wykazali Wolfgang Haken i Kenneth Appel w 1976 roku. Dowód był bardzo złożony i polegał na sprawdzeniu z pomocą komputera niemalże dwóch tysięcy szczególnych przypadków. Było to pierwsze w historii użycie komputera do przeprowadzenia dowodu matematycznego.

Układanie planu lekcji

Kolorowanie grafu okazuje się przydatne choćby przy układaniu planów lekcji.

Dana jest lista przedmiotów, dla których jedna lekcja trwa 45 minut. Niestety niektóre pary zajęć kolidują ze sobą i  z różnych powodów nie mogą odbyć się o tej samej godzinie - na przykład jeśli obejmują tę samą grupę uczniów.

Załóżmy, że naszym zadaniem jest przypisanie poszczególnym zajęciom godziny rozpoczęcia. Optymistycznie dążymy do tego, aby cały plan zajmował jak najmniej godzin. Problem sformułowany w ten sposób znajduje rozwiązanie w teorii grafów.

Lista konfliktów przedmiotów może zostać potraktowana jak lista sąsiedztwa grafu. Każde dwa przedmioty, które ze sobą kolidują, zostaną połączone krawędzią. Jeden przedział czasowy odpowiada kolorowi, który przypiszemy wierzchołkom, czyli zajęciom. Przykładowe kolorowanie możemy zobaczyć na powyższym rysunku.

Planowanie przydziału miejsc

Jeszcze innym zastosowaniem kolorowania grafu może być planowanie układu miejsc dla gości w ramach spotkań towarzyskich czy dużych przyjęć. Przyjrzyjmy się temu na przykładzie niewielkiej grupy.

Mając daną listę gości, przydzielamy im poszczególne miejsca przy pewnej liczbie stołów. Możemy się spodziewać, że niektórzy z gości będą się znali, wobec tego chcemy, aby zasiedli przy tym samym stole. Załóżmy również, że pewni uczestnicy nie przepadają za sobą, więc najlepiej będzie, jeśli dostaną miejsca przy osobnych stołach.

Dla tak sformułowanej sytuacji możemy postawić kilka pytań:

• Ile wynosi minimalna liczba stołów potrzebnych do zaplanowania miejsc, tak aby każdy z gości był zadowolony?

• Jakie może być przykładowe przypisanie miejsc gościom przy wykorzystaniu najmniejszej liczby stołów?

• Jeśli liczba stołów i miejsc przy stole jest ograniczona, to czy możliwe jest takie przydzielenie miejsc, aby nie doszło do spotkania dwójki nieprzepadających za sobą gości przy jednym stole?

• Ile minimalnie miejsc potrzeba na każdy stolik, aby było to możliwe przy ograniczonej liczbie stołów?

Problem przydzielania miejsc dla gości możemy przedstawić, odwołując się do teorii grafów. Każdy wierzchołek niech odpowiada jednemu uczestnikowi. Jeśli dwóch gości nie przepada za sobą, wówczas łączymy krawędzią odpowiadające im wierzchołki.

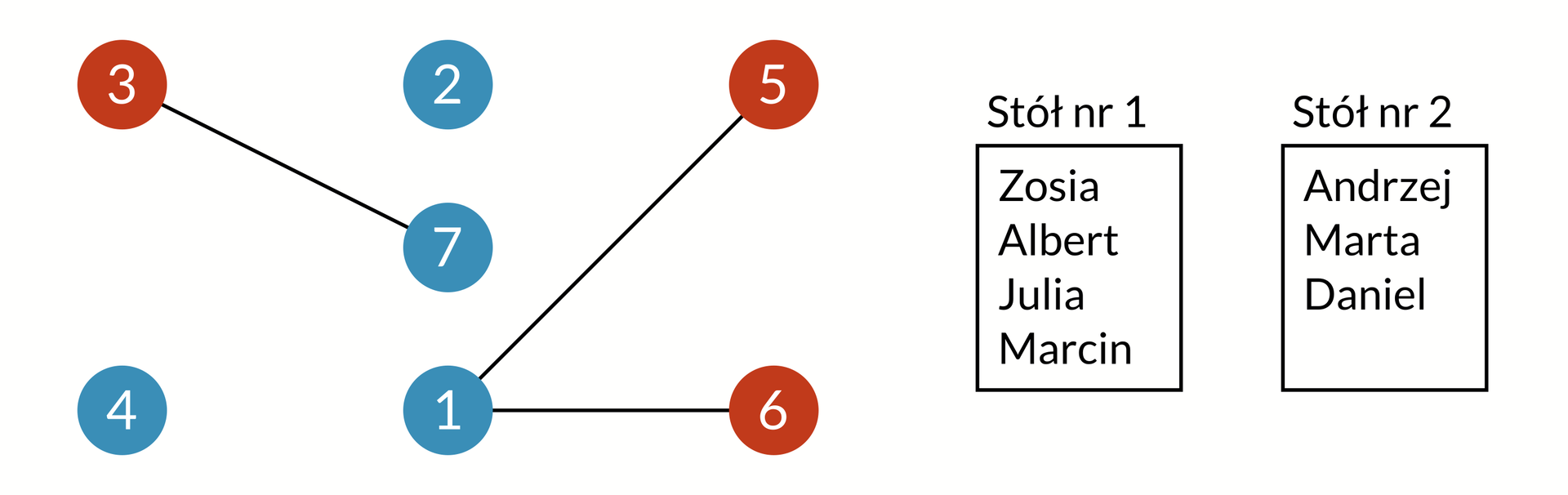
Przypisywanie stołów gościom jest równoznaczne z kolorowaniem wierzchołków grafu. Numer stołu to w istocie numer koloru. Goście, w przypadku których reprezentujące ich wierzchołki mają ten sam kolor, zasiądą przy jednym stole. Na powyższym rysunku został przedstawiony jeden z wielu możliwych podziałów gości na stoły.

Słownik