Funkcją liniowąfunkcja liniowaFunkcją liniową nazywamy funkcję określoną wzorem $f\left(x\right)=ax+b$, gdzie $a$, $b\in \mathrm{ℝ}$.

Na rysunku przedstawiono prostą, będącą wykresem funkcji liniowej określonej wzorem $f\left(x\right)=ax+b$.

R1aIrvhHvMqe6

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 7 do 3 i pionową osią y od minus 5 do trzy. W układzie zaznaczono ukośną prostą o równaniu $f\left(x\right)=ax+b$. Prosta ta przechodzi przez punkt A o współrzędnych nawias minus cztery średnik minus jeden zamknięcie nawiasu oraz punkt B o współrzędnych nawias dwa średnik minus cztery zamknięcie nawiasu.

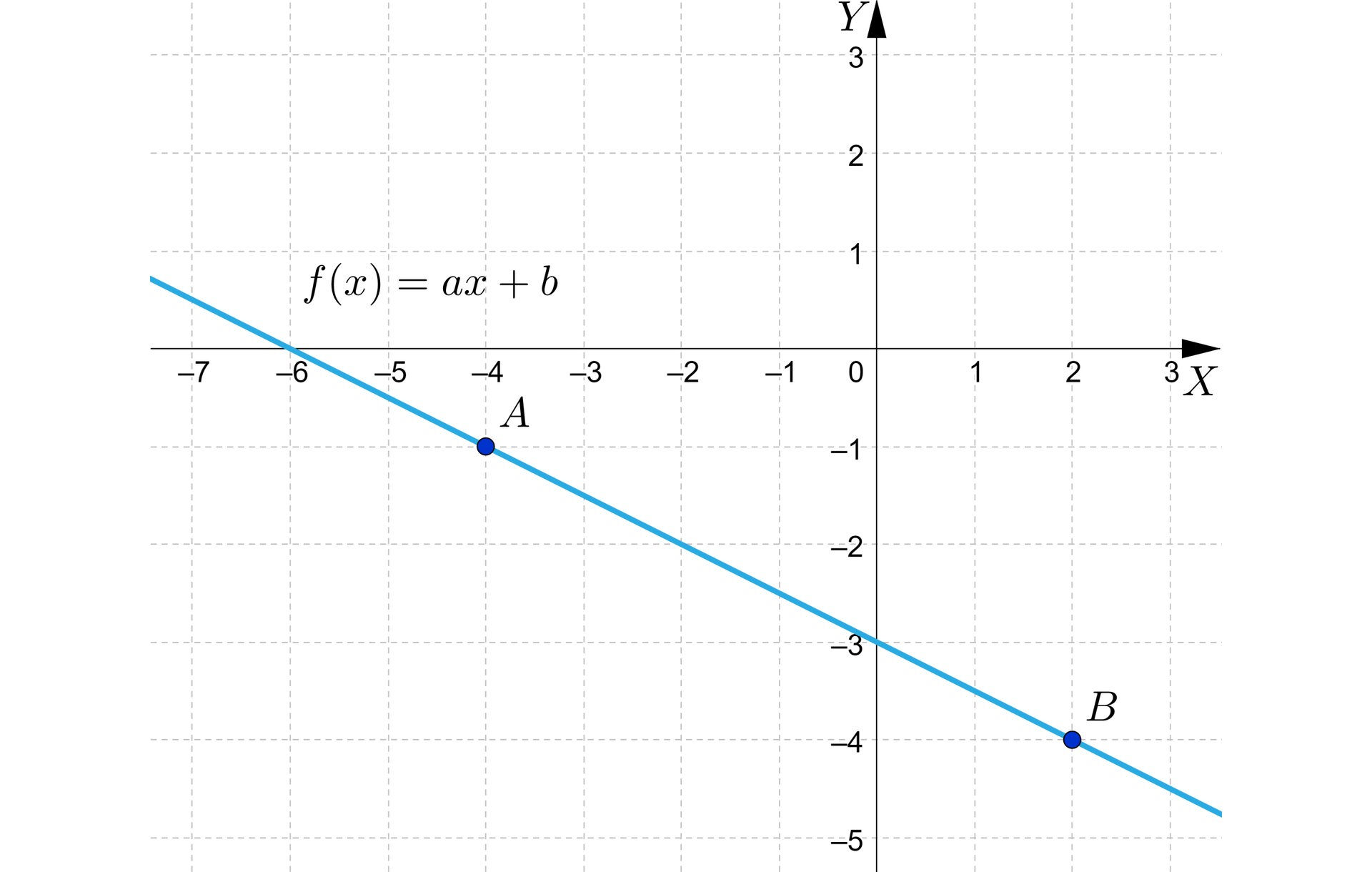
Wyznaczymy wzór tej funkcji.

Rozwiązanie:

Funkcja liniowa jest określona wzorem $f\left(x\right)=ax+b$.

Z wykresu odczytujemy współrzędne punktów $A$ i $B$.

Zatem $A=\left(-4,-1\right)$ i $B=\left(2,-4\right)$.

Podstawiamy współrzędne punktów do wzoru funkcji i otrzymujemy układ równań:

$\left\{\begin{array}{l}-1=a·\left(-4\right)+b\\ -4=a·2+b\end{array}\right.$

Rozwiązaniami układu równań są liczby $a=-\frac{1}{2}$ oraz $b=-3$.

Zatem funkcja liniowa jest określona wzorem $f\left(x\right)=-\frac{1}{2}x-3$.

Na rysunku przedstawiono prostą, będącą wykresem funkcji liniowej określonej wzorem $f\left(x\right)=ax+b$.

R5MkWHg0ov87G

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 7 do 3 i pionową osią y od minus 4 do cztery. W układzie zaznaczono ukośną prostą o równaniu $f\left(x\right)=ax+b$. Prosta ta przechodzi przez punkt A o współrzędnych nawias zero średnik dwa zamknięcie nawiasu oraz punkt B o współrzędnych nawias dwa średnik minus cztery zamknięcie nawiasu.

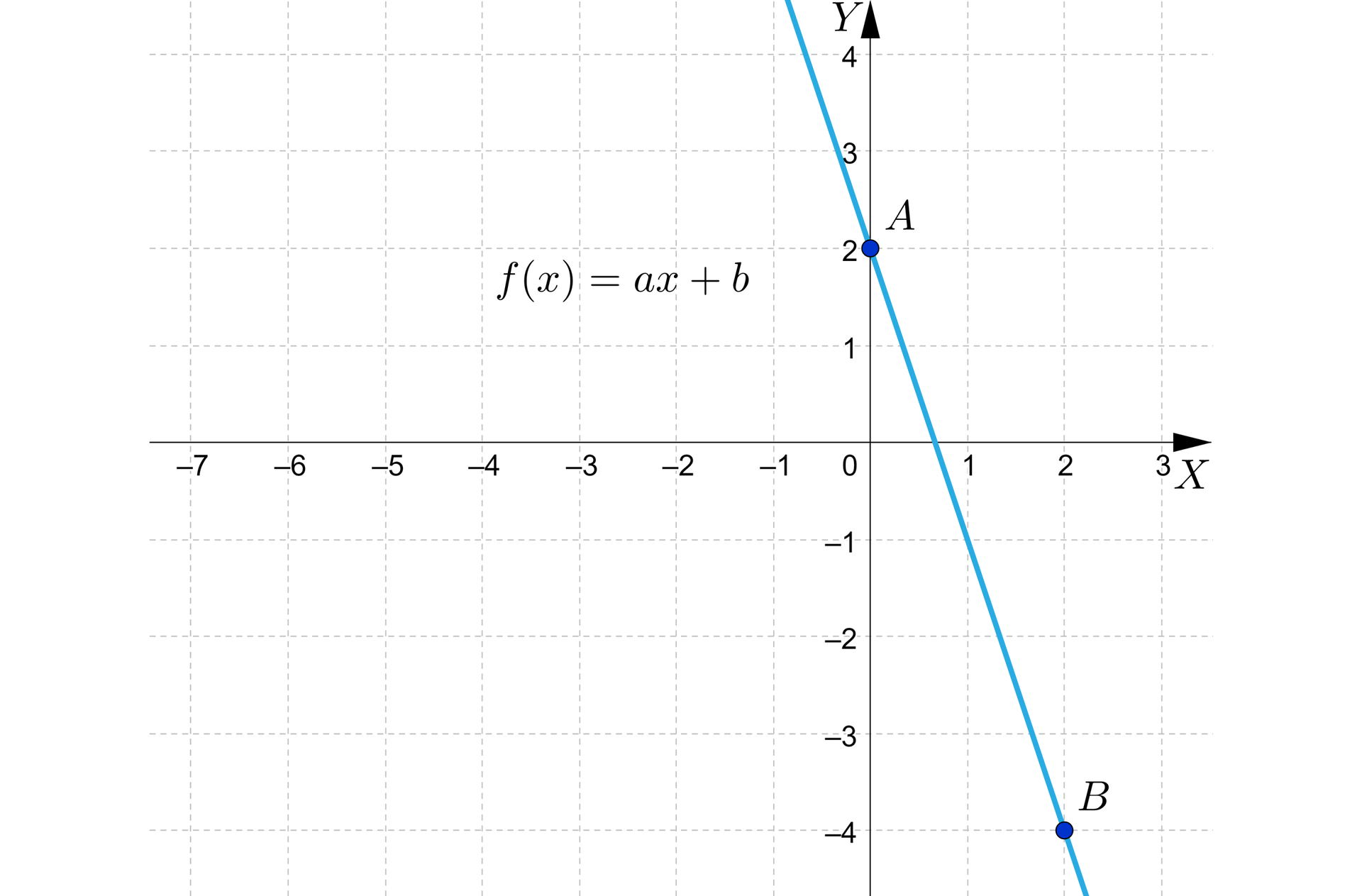
Wyznaczymy wzór tej funkcji.

Rozwiązanie:

Funkcja liniowa jest określona wzorem $f\left(x\right)=ax+b$.

Z wykresu odczytujemy współrzędne punktu $A$, który znajduje się na osi   $Y$ oraz punktu $B$:

$A=\left(0,2\right)$,

$B=\left(2,-4\right)$.

Jeżeli punkt $A$ leży na osi $Y$, to wartość $b=2$.

Zatem wzór funkcji zapisujemy w postaci $f\left(x\right)=ax+2$.

W celu wyznaczenia wartości $a$ podstawiamy współrzędne punktu $B$ do wzoru funkcji i rozwiązujemy równanie:

$-4=a·2+2$, zatem $a=-3$.

Zatem funkcja liniowa jest określona wzorem $f\left(x\right)=-3x+2$.

Prosta, będąca wykresem funkcji liniowej przecina oś $X$ w punkcie o współrzędnych $\left(\frac{1}{2},0\right)$, a oś $Y$ w punkcie o współrzędnych $\left(0,\frac{2}{3}\right)$.

Wyznaczymy wzór tej funkcji.

Rozwiązanie:

Jeżeli prosta, będąca wykresem funkcji liniowej określonej wzorem $f\left(x\right)=ax+b$ przecina oś $Y$ w punkcie o współrzędnych $\left(0,\frac{2}{3}\right)$, to $b=\frac{2}{3}$.

Zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$0=a·\frac{1}{2}+\frac{2}{3}$.

Wobec tego $a=-\frac{4}{3}$.

Funkcja jest określona wzorem $f\left(x\right)=-\frac{4}{3}x+\frac{2}{3}$.

Wyznaczymy wzór funkcji liniowej, jeżeli wiadomo, że do prostej, będącej wykresem tej funkcji należy punkt o współrzędnych $\left(5,-1\right)$, a funkcja przyjmuje wartości dodatnie tylko dla argumentów większych od $10$.

Rozwiązanie:

Jeżeli funkcja przyjmuje wartości dodatnie dla argumentów większych od $10$, to do wykresu tej funkcji należy punkt o współrzędnych $\left(10,0\right)$.

Funkcję liniową określamy wzorem $f\left(x\right)=ax+b$, zatem do wyznaczenia wartości współczynników $a$ i $b$ rozwiązujemy układ równań:

$\left\{\begin{array}{l}-1=a·5+b\\ 0=a·10+b\end{array}\right.$

Po rozwiązaniu układu równań otrzymujemy, że $a=\frac{1}{5}$ oraz $b=-2$ .

Funkcja jest określona wzorem $f\left(x\right)=\frac{1}{5}x-2$.

Wyznaczymy wzór funkcji liniowej, jeżeli wiadomo, że do wykresu tej funkcji należy punkt o współrzędnych $\left(5,-2\right)$, a prosta, będąca wykresem tej funkcji przecina oś $X$ w punkcie o odciętej równej $3$.

Rozwiązanie:

Jeżeli prosta, będąca wykresem funkcji liniowej przecina oś $X$ w punkcie o odciętej równej $3$, to do wykresu tej funkcji należy punkt o współrzędnych $\left(3,0\right)$.

Funkcję liniową określamy wzorem $f\left(x\right)=ax+b$, zatem do wyznaczenia $a$ i $b$ rozwiązujemy układ równań:

$\left\{\begin{array}{l}-2=a·5+b\\ 0=a·3+b\end{array}\right.$

Po rozwiązaniu układu równań otrzymujemy, że $a=-1$ oraz $b=3$.

Wobec tego funkcja liniowa wyraża się wzorem $f\left(x\right)=-x+3$.

Wyznaczymy równania prostych, w których zawarte są boki trójkąta $ABC$ z rysunku.

Ry9mNiiWMQHM1

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do pięć. W układzie zaznaczono trójkąt o wierzchołkach A B C. Współrzędne punktu A to: nawias minus trzy średnik trzy zamknięcie nawiasu. Współrzędne punktu B to: nawias dwa średnik jeden zamknięcie nawiasu. Współrzędne punktu C to: nawias trzy średnik pięć zamknięcie nawiasu.

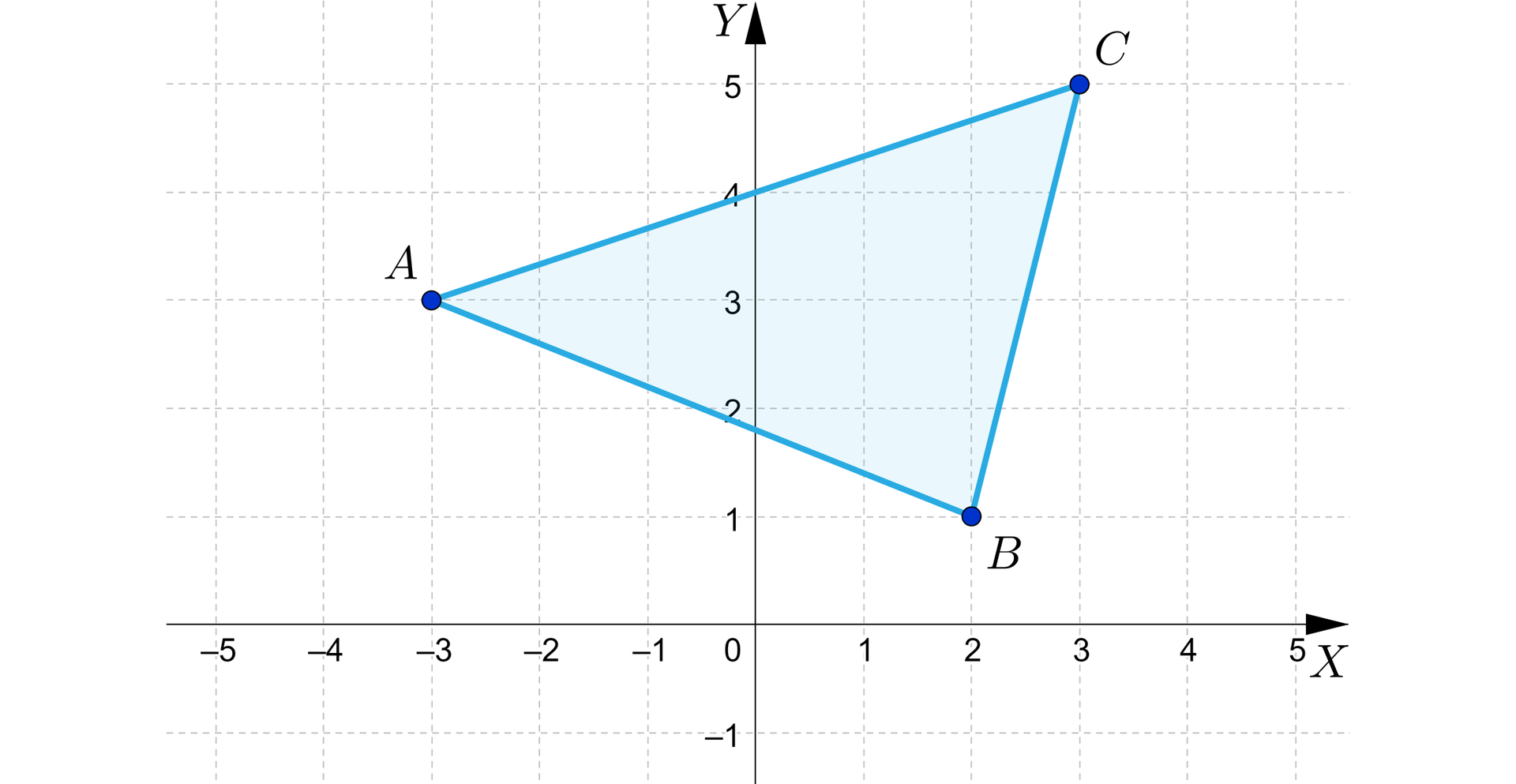
Rozwiązanie:

Z rysunku odczytujemy współrzędne punktów:

$A=\left(-3,3\right)$,

$B=\left(2,1\right)$,

$C=\left(3,5\right)$.

Wyznaczamy równania prostych.

I. Prosta $AB$.

Podstawiamy współrzędne punktów $A$ i $B$ do wzoru $f\left(x\right)=ax+b$ i rozwiązujemy układ równań:

$\left\{\begin{array}{l}3=a·\left(-3\right)+b\\ 1=a·2+b\end{array}\right.$

Zatem $a=-\frac{2}{5}$ i $b=\frac{9}{5}$.

Wobec tego prosta jest opisana równaniem $y=-\frac{2}{5}x+\frac{9}{5}$.

II. Prosta $BC$.

Podstawiamy współrzędne punktów $B$ i $C$ do wzoru $f\left(x\right)=ax+b$ i rozwiązujemy układ równań:

$\left\{\begin{array}{l}1=a·2+b\\ 5=a·3+b\end{array}\right.$

Zatem $a=4$ i $b=-7$.

Wobec tego prosta  jest opisana równaniem $y=4x-7$.

III. Prosta $AC$.

Podstawiamy współrzędne punktów $A$ i $C$ do wzoru $f\left(x\right)=ax+b$ i rozwiązujemy układ równań:

$\left\{\begin{array}{l}3=a·\left(-3\right)+b\\ 5=a·3+b\end{array}\right.$

Zatem $a=\frac{1}{3}$ i $b=4$.

Wobec tego prosta jest opisana równaniem $y=\frac{1}{3}x+4$.

funkcja określona wzorem $f\left(x\right)=ax+b$, gdzie $a$,$b$ ∈ $\mathrm{ℝ}$