Przeczytaj

funkcja kwadratowa

Definicja: funkcja kwadratowa

Funkcję określoną wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c$ ∈ $ℝ$ , $a \neq 0$ , $x \in ℝ$ oraz $f (x) \in ℝ$ nazywamy funkcją kwadratowąfunkcja kwadratowafunkcją kwadratową.

Zajmiemy się szczególnym przypadkiem funkcji kwadratowej, określonej za pomocą wzoru $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a \neq 0$ .

Ważne!

Wykres funkcji kwadratowej nazywamy parabolą. W paraboliparabolaparaboli możemy wyróżnić wierzchołek oraz ramiona.

Poznamy własności funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a \neq 0$ , jeżeli:

$a > 0$ ,
$a < 0$ .

Własności funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a > 0$ .

Pomocniczo naszkicujmy wykres funkcji kwadratowej określonej wzorem $f (x) = x^{2}$ .

W tym celu, w tabeli przedstawimy wartości tej funkcji dla kilku argumentów.

Argumenty i wartości funkcji
$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$4$	$1$	$0$	$1$	$4$

Wykres tej funkcji przedstawia się następująco:

R4yLwsdp8kc5c

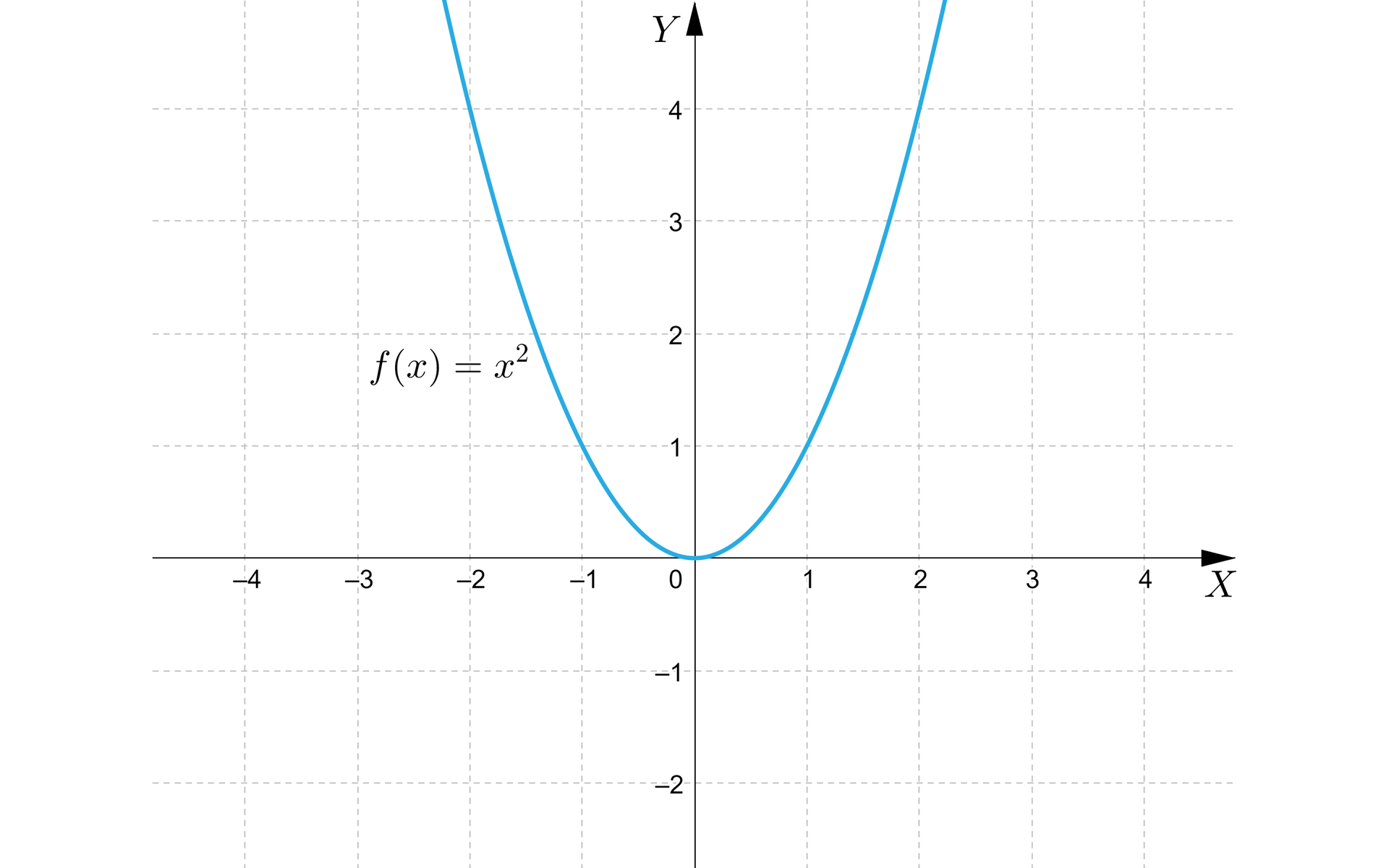
Ilustracja przedstawia układ współrzędnych z poziomą osią od minus 4 do czterech oraz osią pionową od minus 2 do czterech. Zaznaczono parabolę z ramionami skierowanymi w górę oraz wierzchołkiem w środku układu współrzędnych.

Niezależnie od wyboru wartości współczynnika $a$ , gdy $a > 0$ , dla funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , określamy następujące własności:

dziedziną funkcji kwadratowej jest zbiór liczb rzeczywistych, a zbiorem wartości zbiór liczb rzeczywistych nieujemnych,
zachodzi warunek: $f (0) = 0$
osią symetrii paraboli, będącej wykresem takiej funkcji kwadratowej jest prosta o równaniu $x = 0$ .

Udowodnimy ostatnią z podanych własności.

Dowód:

Niech $x \in D_{f}$ . Wtedy:

$f (x) = a \cdot x^{2} = a x^{2}$

$f (- x) = a \cdot {(- x)}^{2} = a x^{2}$

Ponieważ dla dowolnego $x \in D_{f}$ zachodzi warunek:

$f (x) = f (- x)$ , zatem dla dwóch dowolnych argumentów, będących liczbami przeciwnymi, należących do dziedziny tej funkcji, wartości funkcji w tych punktach są takie same.

Zatem osią symetrii paraboli, będącej wykresem funkcji kwadratowej jest prosta o równaniu $x = 0$ .

Ciąg dalszy własności omawianej funkcji:

funkcja kwadratowa jest malejąca w przedziale $(- \infty, 0⟩$ ,
funkcja kwadratowa jest rosnąca w przedziale $⟨0, \infty)$ ,
dla $x = 0$ funkcja $f$ przyjmuje wartość najmniejszą,
$f (x) > 0$ dla $x \in (- \infty, 0) \cup (0, \infty)$ .

Własności funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a < 0$ .

Pomocniczo naszkicujmy wykres funkcji kwadratowej określonej wzorem $f (x) = - x^{2}$ .

W tym celu, w tabeli przedstawimy wartości tej funkcji dla kilku argumentów.

Argumenty i wartości funkcji
$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$- 4$	$- 1$	$0$	$- 1$	$- 4$

Wykres tej funkcji przedstawia się następująco:

R1PozZNPi2drr

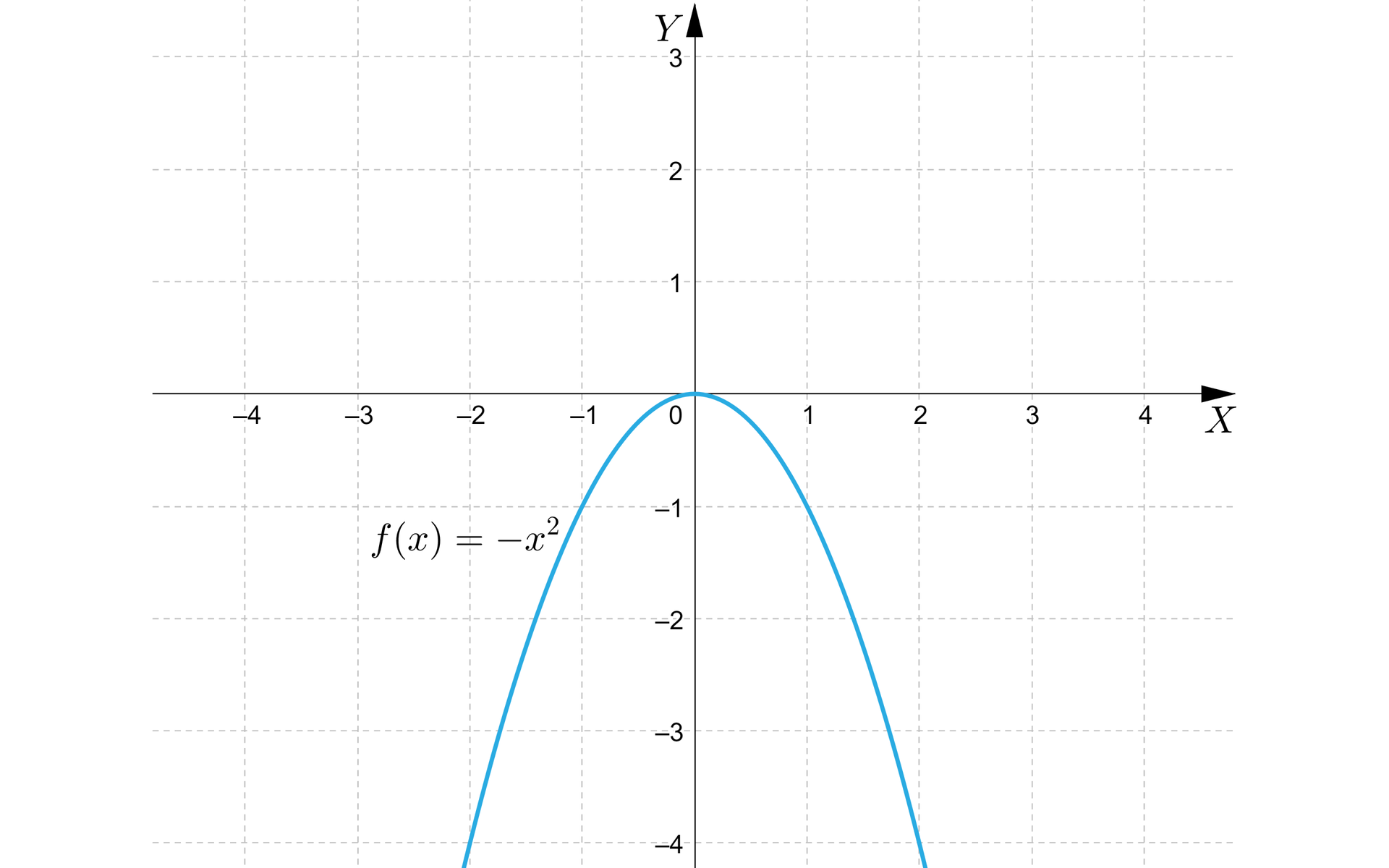
Ilustracja przedstawia układ współrzędnych z poziomą osią od minus 4 do czterech oraz osią pionową od minus 4 do trzech. Zaznaczono parabolę z ramionami skierowanymi w dół oraz wierzchołkiem w środku układu współrzędnych.

Niezależnie od wyboru wartości współczynnika $a$ , gdy $a < 0$ , dla funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , określamy następujące własności:

dziedziną funkcji kwadratowej jest zbiór liczb rzeczywistych, a zbiorem wartości zbiór liczb rzeczywistych niedodatnich,
zachodzi warunek: $f (0) = 0$ ,
osią symetrii paraboli, będącej wykresem funkcji kwadratowej $f$ jest prosta o równaniu $x = 0$ ,
funkcja kwadratowa jest rosnąca w przedziale $(- \infty, 0⟩$ ,
funkcja kwadratowa jest malejąca w przedziale $⟨0, \infty)$ ,
dla $x = 0$ funkcja $f$ przyjmuje wartość największą,
$f (x) < 0$ dla $x \in (- \infty, 0) \cup (0, \infty)$ .

Wniosek: wartość współczynnika $a$ we wzorze funkcji kwadratowej $f (x) = a x^{2}$ decyduje o tym, czy ramiona paraboli, będącej wykresem funkcji kwadratowej są skierowane do góry, czy do dołu.

Ciekawostka

Wykresy funkcji kwadratowych określonych wzorami $f (x) = a x^{2}$ oraz $f (x) = - a x^{2}$ dla $a \neq 0$ są symetryczne względem osi $X$ układu współrzędnych.

Jeżeli znamy współrzędne punktu, który należy do wykresu funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , wówczas możemy wyznaczyć wartość współczynnika $a$ .

Przykład 1

Wyznaczymy wartość współczynnika $a$ , jeżeli wiadomo, że punkt $P$ o współrzędnych $P = (\sqrt{2}, - 4)$ należy do paraboli, będącej wykresem funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ .

W celu wyznaczenia wartości współczynnika $a$ , podstawiamy współrzędne punktu $P$ do wzoru $f (x) = a x^{2}$ i rozwiązujemy otrzymane równanie:

$- 4 = a \cdot {(\sqrt{2})}^{2}$ .

Równanie przekształcamy do postaci $- 4 = 2 a$ , zatem $a = - 2$ .

Przykład 2

Wyznaczymy podzbiór zbioru wartości funkcji kwadratowej określonej wzorem $f (x) = 3 x^{2}$ , jeżeli podzbiorem dziedziny tej funkcji jest zbiór $D = ⟨- 1, 2⟩$ .

Zauważmy, że:

ramiona paraboli, która jest wykresem tej funkcji są skierowane do góry,
dla $x = 0$ funkcja osiąga wartość najmniejszą i liczba zero należy do danego przedziału, zatem $f (0) = 3 \cdot 0^{2} = 0$ ,
$f (- 1) = 3 \cdot {(- 1)}^{2} = 3$ ,
$f (2) = 3 \cdot 2^{2} = 12$ .

Zatem podzbiorem zbioru wartości rozpatrywanej funkcji jest przedział $⟨0, 12⟩$ , bo najmniejsza wartość funkcji w rozpatrywanym przedziale wynosi $0$ , a największa wartość funkcji jest osiągana w jednym z końców przedziału $⟨- 1, 2⟩$ (z uwagi na to, że ramiona wykresu są skierowane do góry).

Wartość współczynnika $a$ decyduje o tym, jak oddalone są od osi rzędnych układu współrzędnych punkty należące do ramion paraboliparabolaparaboli, która jest wykresem funkcji określonej wzorem $f (x) = a x^{2}$ .

Przykład 3

Naszkicujemy w jednym układzie współrzędnych wykresy funkcji określonych wzorami $f (x) = \frac{1}{2} x^{2}$ , $g (x) = \frac{1}{3} x^{2}$ oraz $h (x) = \frac{1}{4} x^{2}$ . Sformułujemy wniosek dotyczący punktów należących do ramion paraboli, będących wykresami funkcji kwadratowych.

RjiWKmHgKv15z

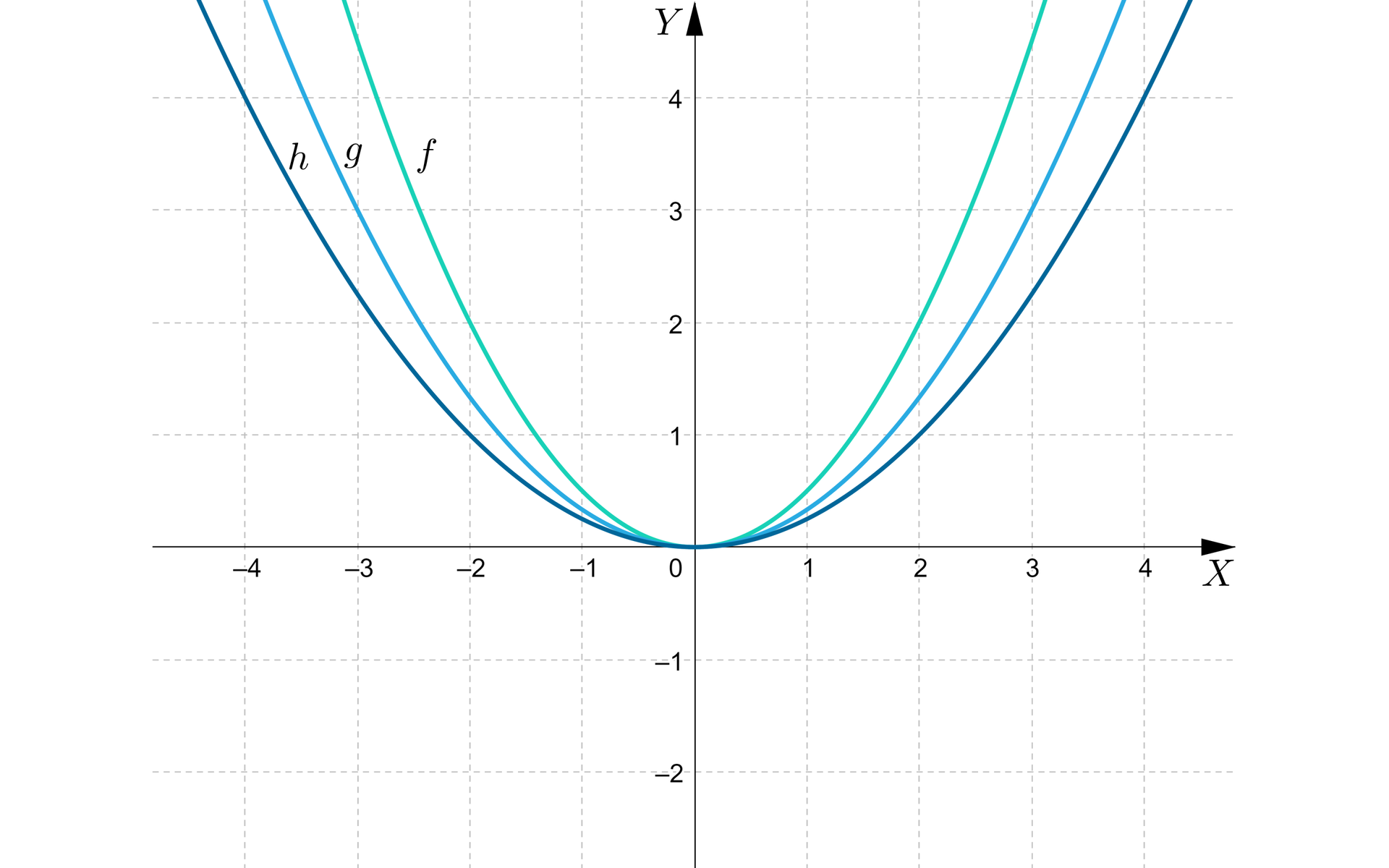
Ilustracja przedstawia układ współrzędnych z poziomą osią od minus 4 do czterech oraz osią pionową od minus 2 do czterech. Zaznaczono trzy parabolę mające ramiona skierowane w górę oraz wierzchołek w początku układu współrzędnych. Parabola f ma dwa punkty charakterystyczne -2;2 oraz 2;2. Parabola g ma dwa punkty charakterystyczne -3;3 oraz 3;3. Parabola h ma dwa punkty charakterystyczne -4;4 oraz 4;4.

Rozwiązanie:

Niech $x \in D_{f} = D_{g} = D_{h}$ .

Wraz ze wzrostem wartości współczynnika $a$ , odległości punktów $(x, h (x))$ , $(x, g (x))$ oraz $(x, f (x))$ od osi rzędnych układu współrzędnych są coraz mniejsze.

Przykład 4

Sprawdzimy, czy punkty o współrzędnych $(- \sqrt{2}, 4)$ oraz $(\sqrt{3}, 9)$ należą do paraboli, będącej wykresem tej samej funkcji kwadratowej, określonej za pomocą wzoru $f (x) = a x^{2}$ .

Rozwiązanie:

Jeżeli punkt o współrzędnych $(- \sqrt{2}, 4)$ należy do wykresu funkcji kwadratowej określonej za pomocą wzoru $f (x) = a x^{2}$ , to w celu wyznaczenia wartości $a$ rozwiązujemy równanie:

$4 = a \cdot {(- \sqrt{2})}^{2}$ .

Zatem $2 a = 4$ , więc $a = 2$ .

Funkcja jest opisana za pomocą wzoru $f (x) = 2 x^{2}$ .

Sprawdzimy, czy punkt o współrzędnych $(\sqrt{3}, 9)$ należy do wykresu tej funkcji.

$f (\sqrt{3}) = 2 \cdot {(\sqrt{3})}^{2} = 6 \neq 9$ .

Zatem podane punkty nie należą do paraboli, będącej wykresem tej samej funkcji kwadratowej.

Przykład 5

Wykażemy, że funkcja kwadratowa określona wzorem $f (x) = a x^{2}$ , dla $a > 0$ jest malejąca w przedziale $(- \infty, 0⟩$ .

Rozwiązanie:

Załóżmy, że $x_{1}, x_{2} \in D_{f}$ , $x_{1} < x_{2}$ oraz $x_{1}, x_{2} \in (- \infty, 0⟩$ .

Wtedy

$f (x_{2}) - f (x_{1}) = a x_{2}^{2} - a x_{1}^{2} = a (x_{2} - x_{1}) (x_{2} + x_{1})$

Ponieważ $x_{1} < x_{2}$ , zatem $a \cdot (x_{2} - x_{1}) \cdot (x_{2} + x_{1}) < 0$ , bo:

dla $x_{1} < x_{2}$ mamy $x_{2} - x_{1} > 0$
dla $x_{1}, x_{2} \in (- \infty, 0⟩$ mamy $x_{2} + x_{1} < 0$

Zatem $f (x_{1}) > f (x_{2})$ .

Stąd, wobec dowolności $x_{1}, x_{2}$ wnioskujemy, że funkcja $f$ jest malejąca w przedziale $(- \infty, 0⟩$ .

Słownik

funkcja kwadratowa

funkcja określona wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c$ ∈ $ℝ$ , $a \neq 0$ oraz $x \in ℝ$

parabola

wykres funkcji kwadratowej określonej wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c$ ∈ $ℝ$ oraz $a \neq 0$ , $x \in ℝ$ ,

krzywa będąca zbiorem punktów równoodległych od prostej zwanej kierownicą paraboli i punktu zwanego ogniskiem paraboli

Wprowadzenie

Symulacja interaktywna

Słownik