Przeczytaj
Znamy już podstawowe nazewnictwo związane z elementami ostrosłupa oraz ostrosłupy, których jedna z krawędzi bocznych jest prostopadła do płaszczyzny podstawy. Teraz czas na dokonanie podstawowej klasyfikacji ostrosłupów. Bliżej omówimy dwa rodzaje ostrosłupów, z którymi spotykamy się w szkole najczęściej: ostrosłupy proste i ostrosłupy prawidłowe.
Ostrosłupem prostym nazywamy taki ostrosłup, którego wszystkie krawędzie boczne są tej samej długości.
W zadaniach nie zawsze jest wprost napisane, że omawiany ostrosłup jest prosty. Można to przekazać na wiele sposobów. Aby nie mieć wątpliwości przy klasyfikowaniu ostrosłupa, warto wykorzystać poniższy fakt.
Następujące warunki są równoważne.
Wszystkie krawędzie boczne ostrosłupa są tej samej długości.
Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie ostrosłupa.
Wszystkie krawędzie boczne ostrosłupa są nachylone do płaszczyzny jego podstawy pod tym samym kątem.
Udowodnimy powyższe twierdzenie.
Rozwiązanie
Załóżmy, że wszystkie krawędzie boczne ostrosłupa są tej samej długości. Pokażemy, że spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie ostrosłupa. Posłużymy się przykładowym rysunkiem. Jest na nim ostrosłup prawidłowy sześciokątny. Oczywiście podstawą ostrosłupa może być dowolny wielokąt, na którym można opisać okrąg. Rysunek ma nam tylko pomóc zrozumieć, o jakich trójkątach mówimy.
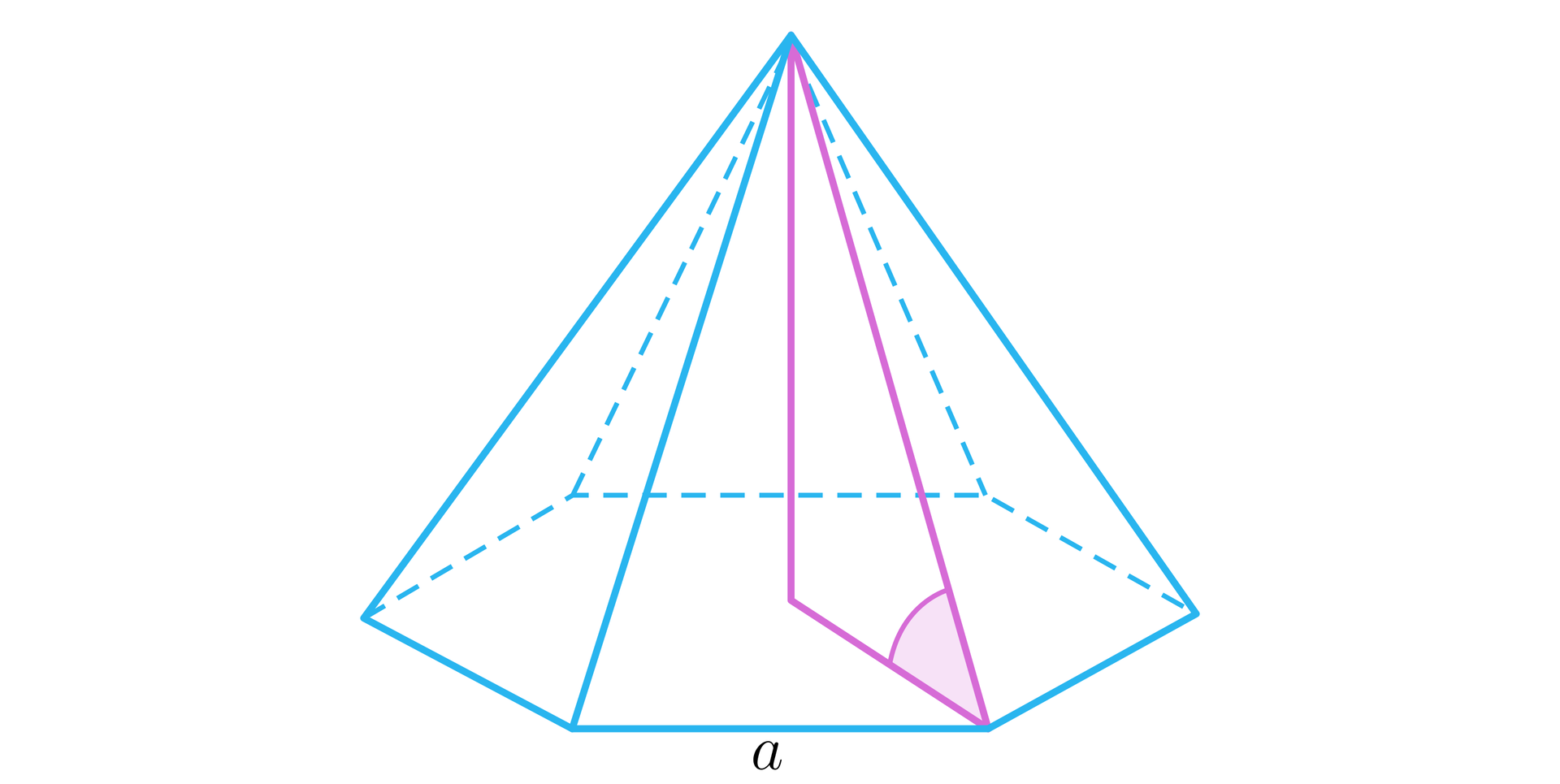
Rozważmy wszystkie trójkąty prostokątne, w których jedną z przyprostokątnych jest wysokość ostrosłupa a przeciwprostokątną krawędź boczna ostrosłupa. Skoro wszystkie krawędzie boczne ostrosłupa są tej samej długościa a wysokość jest ich wspólnym bokiem, to trójkąty te są przystające. Oznacza to, że odległość spodka wysokości od każdego z wierzchołków podstawy jest taka sama. Zatem spodek wysokości jest środkiem okręgu opisanego na podstawie ostrosłupa.
Załóżmy teraz, że spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie ostrosłupa. Oznacza to, że wszystkie trójkąty, w których jedną z przyprostokątnych jest promień okręgu opisanego na podstawie ostrosłupa, a drugą wysokość ostrosłupa są przystające (na mocy twierdzenia Pitagorasa i cechy bbb). Zatem kąt nachylenia każdej krawędzi bocznej do płaszczyzny podstawy jest taki sam.
Załóżmy w końcu, że wszystkie krawędzie boczne ostrosłupa są nachylone do płaszczyzny jego podstawy pod tym samym kątem. Pokażemy, że wszystkie krawędzie boczne ostrosłupa są tej samej długości. Znów, badamy trójkąty prostokątne, w których jedna z przyprostokątnych to wysokość ostrosłupa a przeciwprostokątna to krawędź boczna. Skoro wszystkie krawędzie boczne są nachylone do podstawy pod tym samym kątem, to trójkąty są przystające (cecha kbk). Zatem z podobieństwa trójkątów otrzymujemy, że wszystkie przeciwprostokątne są równej długości. Tym samym wszystkie krawędzie boczne ostrosłupa są tej samej długości.
Poniżej możesz obserwować różne przykłady ostrosłupów prostych. Zwróć uwagę na fakt, że przymiotnik prosty nie oznacza tu kąta prostego, ale pewną regularność widoczną dla krawędzi bocznych ostrosłupa. Zmieniając położenie wierzchołków podstawy zmienisz jej rozmiar i kształt, a zmieniając położenie punktu W zmienisz wysokość ostrosłupa.
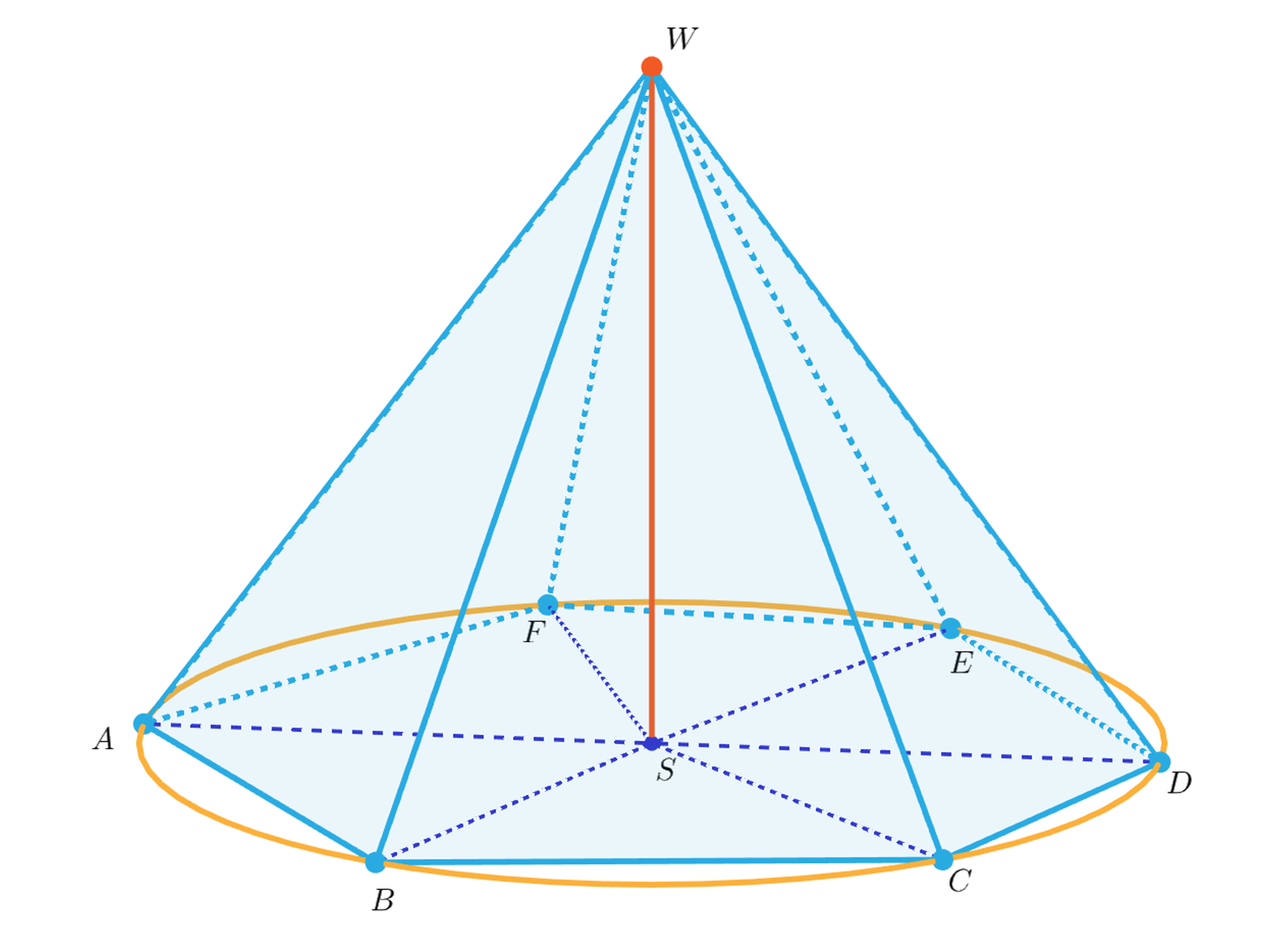
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1Fgb17Su
Jeśli podstawą ostrosłupa jest trójkąt, to ostrosłup nazywamy ostrosłupem trójkątnym lub czworościanem. Jeśli ponadto wszystkie krawędzie ostrosłupa mają tę samą długość, to mówimy o czworościanie foremnym.czworościanie foremnym.. Ostrosłup nazywamy czworokątnym, gdy w podstawie jest czworokąt. Ogólnie, ostrosłup nazywamy ostrosłupem -kątnym, gdy w podstawie ostrosłupa znajduje się -kąt.
Dany jest ostrosłup prosty, którego podstawą jest trójkąt prostokątny o przyprostokątnych długości oraz . Wysokość tego ostrosłupa jest równa . Oblicz sumę długości wszystkich krawędzi tego ostrosłupa.
Rozwiązanie
Zwróćmy uwagę na fakt, że omawiany ostrosłup jest prosty. Oznacza to, że spodek wysokości tego ostrosłupa jest środkiem okręgu opisanego na podstawie. Ponieważ jednak podstawą jest trójkąt prostokątny, to punkt znajduje się dokładnie w połowie przeciwprostokątnej. Wykonujemy odpowiedni szkic do zadania:
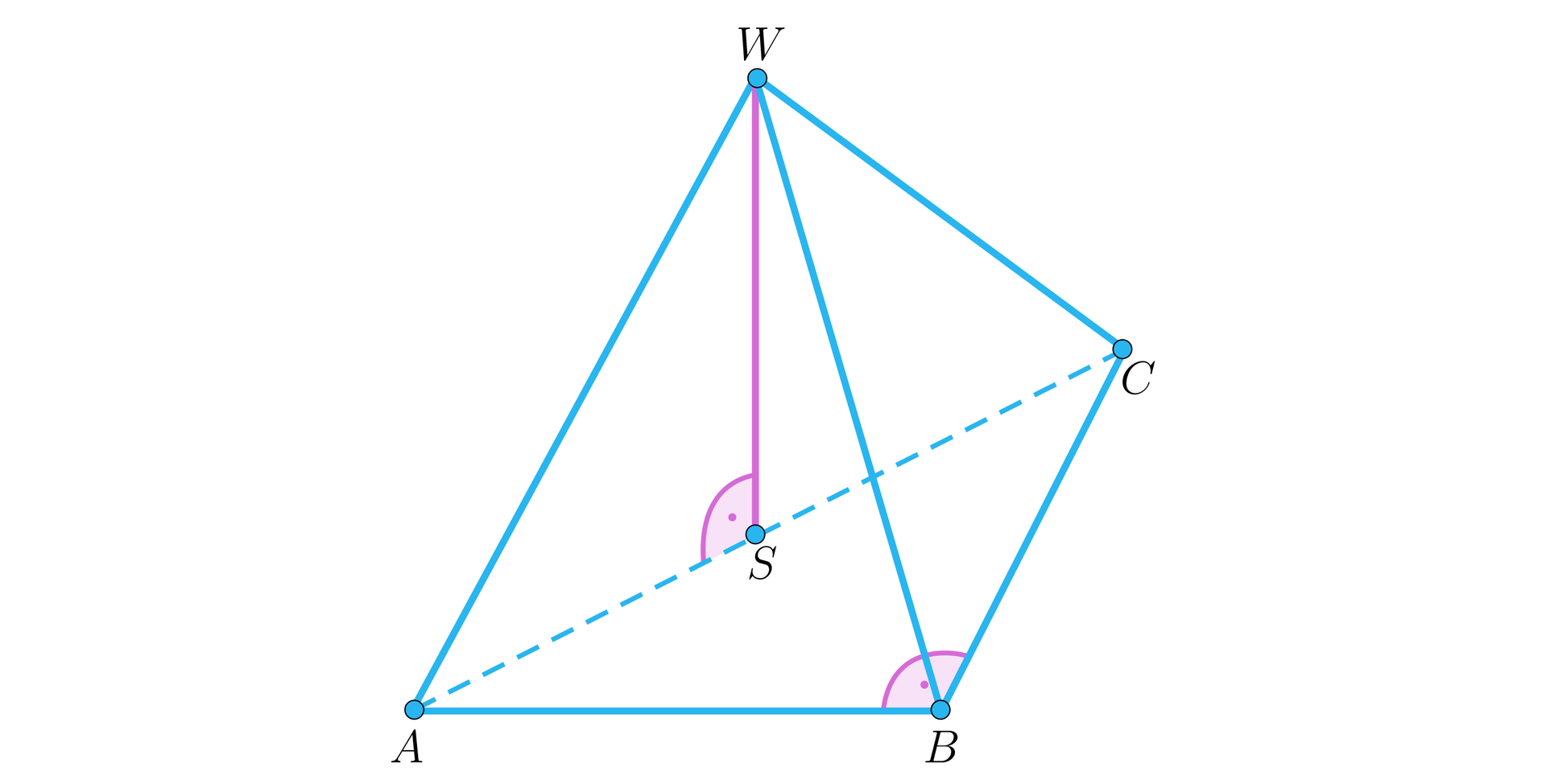
Korzystając z twierdzenia Pitagorasa dla otrzymujemy długość przeciwprostokątnej trójkąta podstawy :
Korzystamy ponownie z faktu, że ostrosłup jest prosty. Oznacza to, że wszystkie jego krawędzie boczne są równej długości. Pozostaje obliczenie długości krawędzi ostrosłupa. W tym celu ponownie możemy wykorzystać twierdzenie Pitagorasa w pamiętając, że promień okręgu opisanego na podstawie ostrosłupa jest tu połową przeciwprostokątnej podstawy:
.
Ostatecznie suma długości wszystkich krawędzi danego ostrosłupa jest równa
Zauważmy, że w rozwiązaniu tego zadania wykorzystaliśmy trójkąt prostokątny zawierający wysokość ostrosłupa, promień okręgu opisanego na jego podstawie i krawędź boczną ostrosłupa. Warto zapamiętać ten krok, gdyż bardzo często jest on wykorzystywany w przypadku ostrosłupów prostych.
Podstawą ostrosłupa jest trapez . Przekątna tego trapezu jest prostopadła do jego ramienia i tworzy z dłuższą podstawą kąt . Wszystkie krawędzie boczne ostrosłupa są równej długości. Wiedząc, że oraz oblicz odległość - spodka wysokości tego ostrosłupa od jego krawędzi bocznej .
Rozwiązanie
Zauważmy, że ostrosłup jest prosty, bo wszystkie jego krawędzie boczne są równej długości. Na trapezie z podstawy można zatem opisać okrąg. Zgodnie z twierdzeniem o okręgu opisanym na czworokącietwierdzeniem o okręgu opisanym na czworokącie, musi to być trapez równoramienny. Rzeczywiście, zauważmy, że dla czworokąta na którym można opisać okrąg mamy:
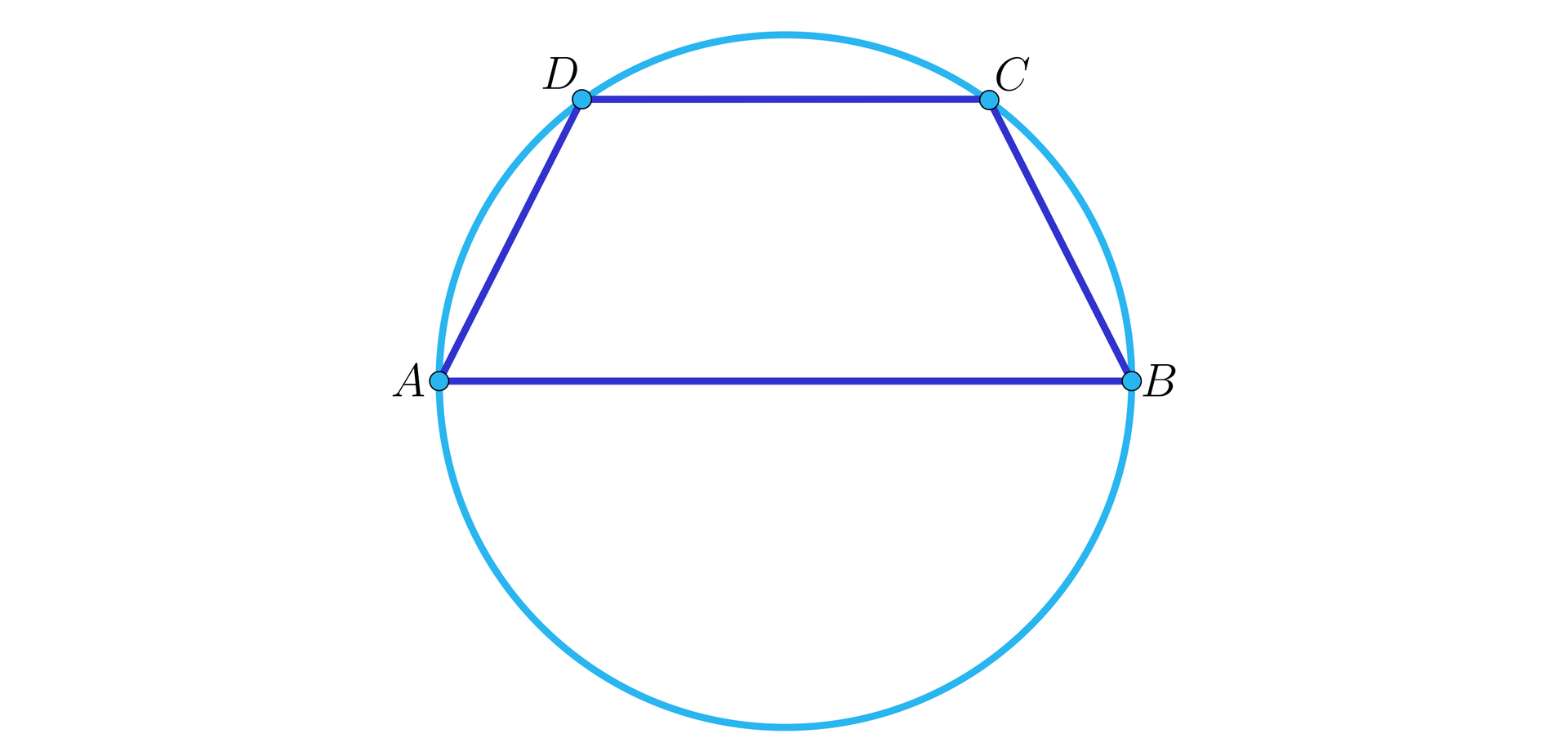
. Jednocześnie dla każdego trapezu wiadomo, że . Ostatecznie .
Przeanalizujmy zatem naszą podstawę.
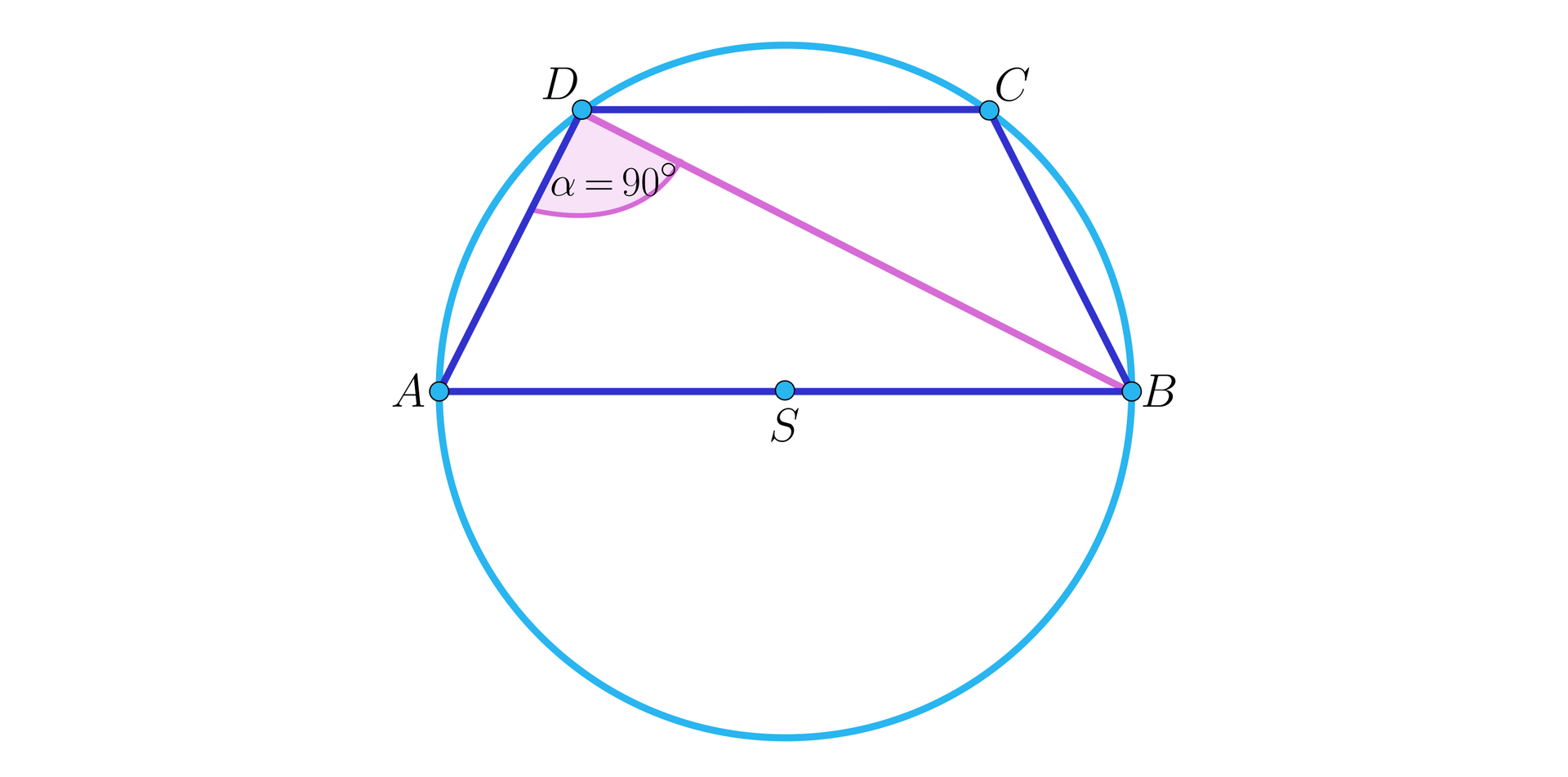
Wiemy, że przekątna jest prostopadła do ramienia . Kąt jest prosty, zatem podstawa trapezu jest średnicą okręgu opisanego na tym trapezie, a środek tego okręgu jest środkiem odcinka . Skoro przekątna trapezu ma długość , to z uwagi na podany kąt mamy . Ostatecznie promień okręgu opisanego na podstawie ma długość . Podsumowując: ostrosłup jest ostrosłupem prostym, którego spodek wysokości znajduje się w połowie krawędzi podstawy .
Naszkicujmy zatem dany ostrosłup:
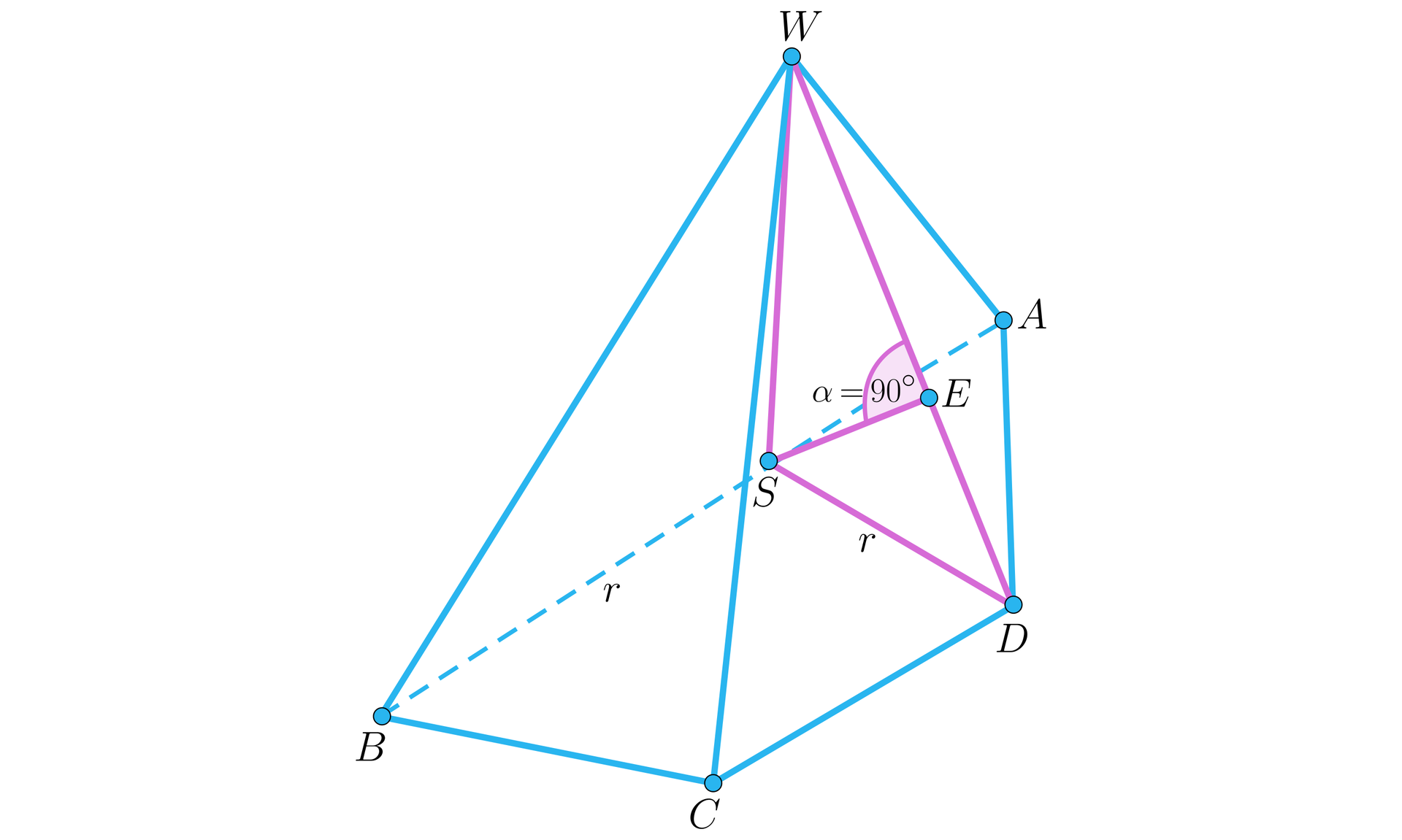
Z trójkąta możemy obliczyć wysokość ostrosłupa:
Trójkąty oraz są podobnepodobne (oba są prostokątne i mają jeden wspólny kąt ostry), stąd:
,
gdzie oznacza szukaną odległość spodka wysokości ostrosłupa od jego krawędzi bocznej .
Oblicz wysokość ostrosłupa trójkątnego, którego siatkę przedstawiono na rysunku.
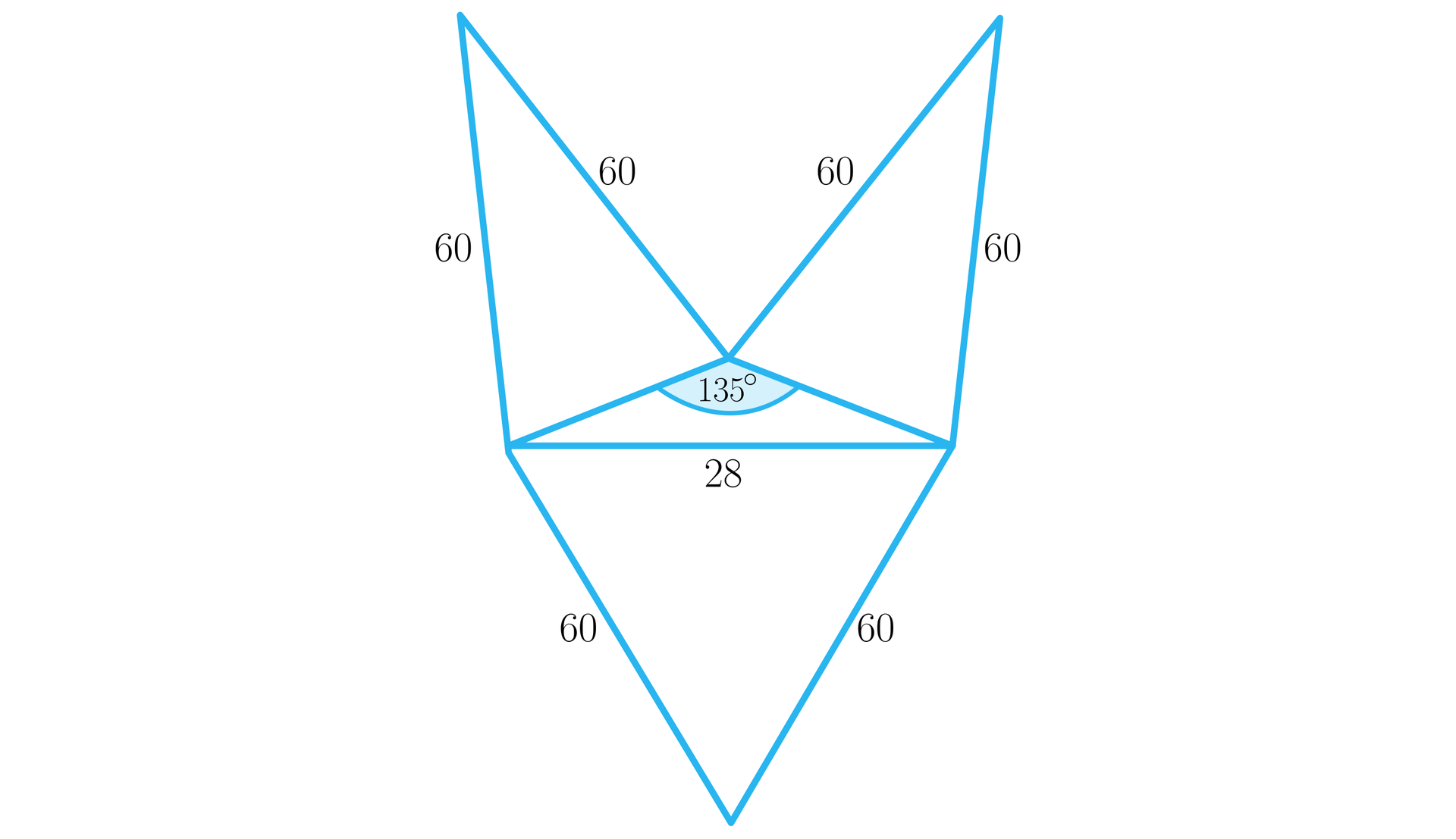
Rozwiązanie
Zauważmy, że tym razem informacja o tym, że ostrosłup jest prosty została podana na rysunku. Skoro długości wszystkich krawędzi bocznych są sobie równe, spodek wysokości tego ostrosłupa znajduje się w środku okręgu opisanego na jego podstawie. Ze względu na fakt, że podstawa jest trójkątem rozwartokątnym, spodek wysokości ostrosłupa będzie się znajdował poza trójkątem. Sprawdźmy na animacji, jak wygląda taki ostrosłup:
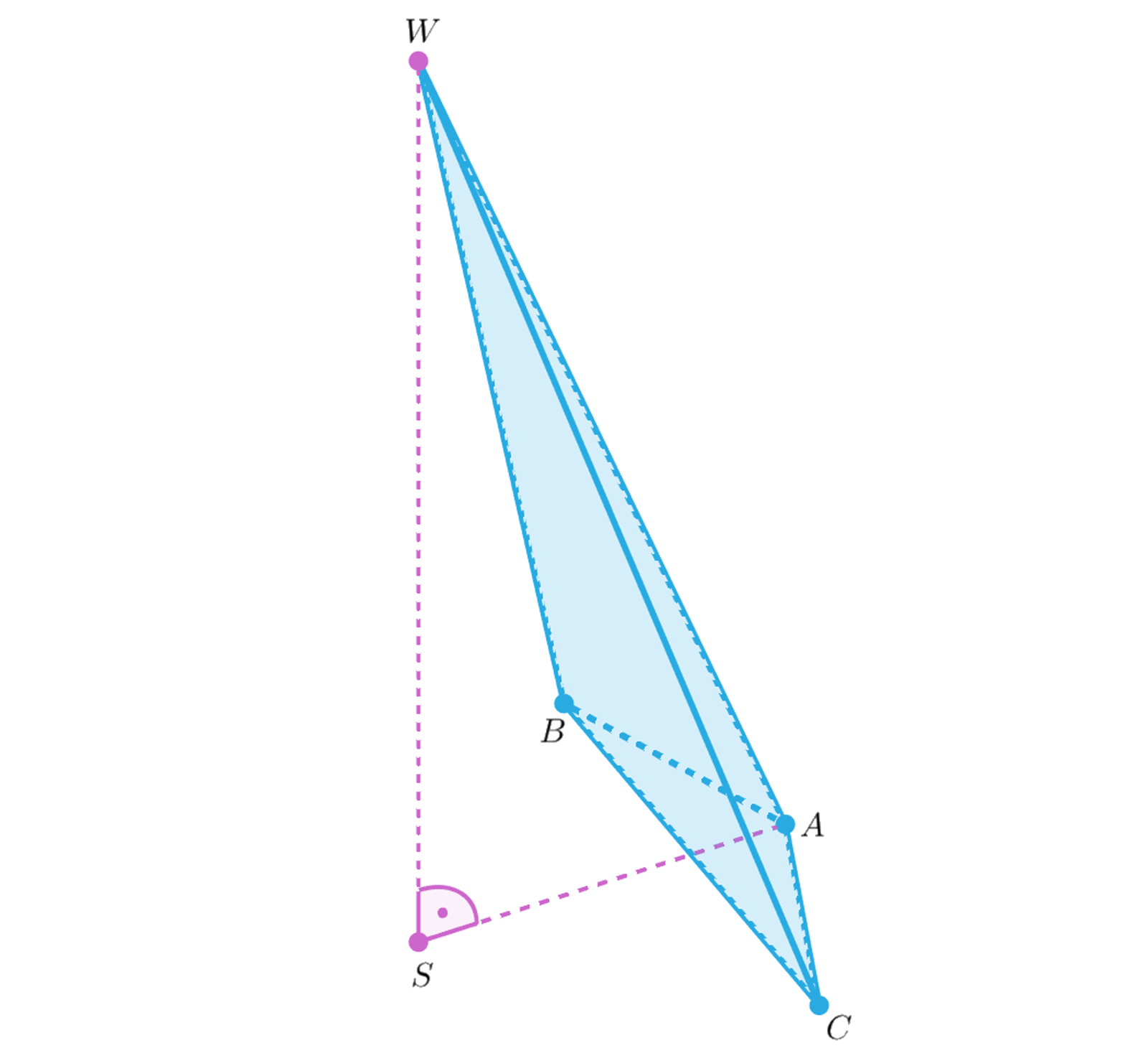
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1Fgb17Su
Naszkicujmy ostrosłup spełniający warunki zadania, aby przyjąć oznaczenia potrzebne do zapisu rozwiązania:
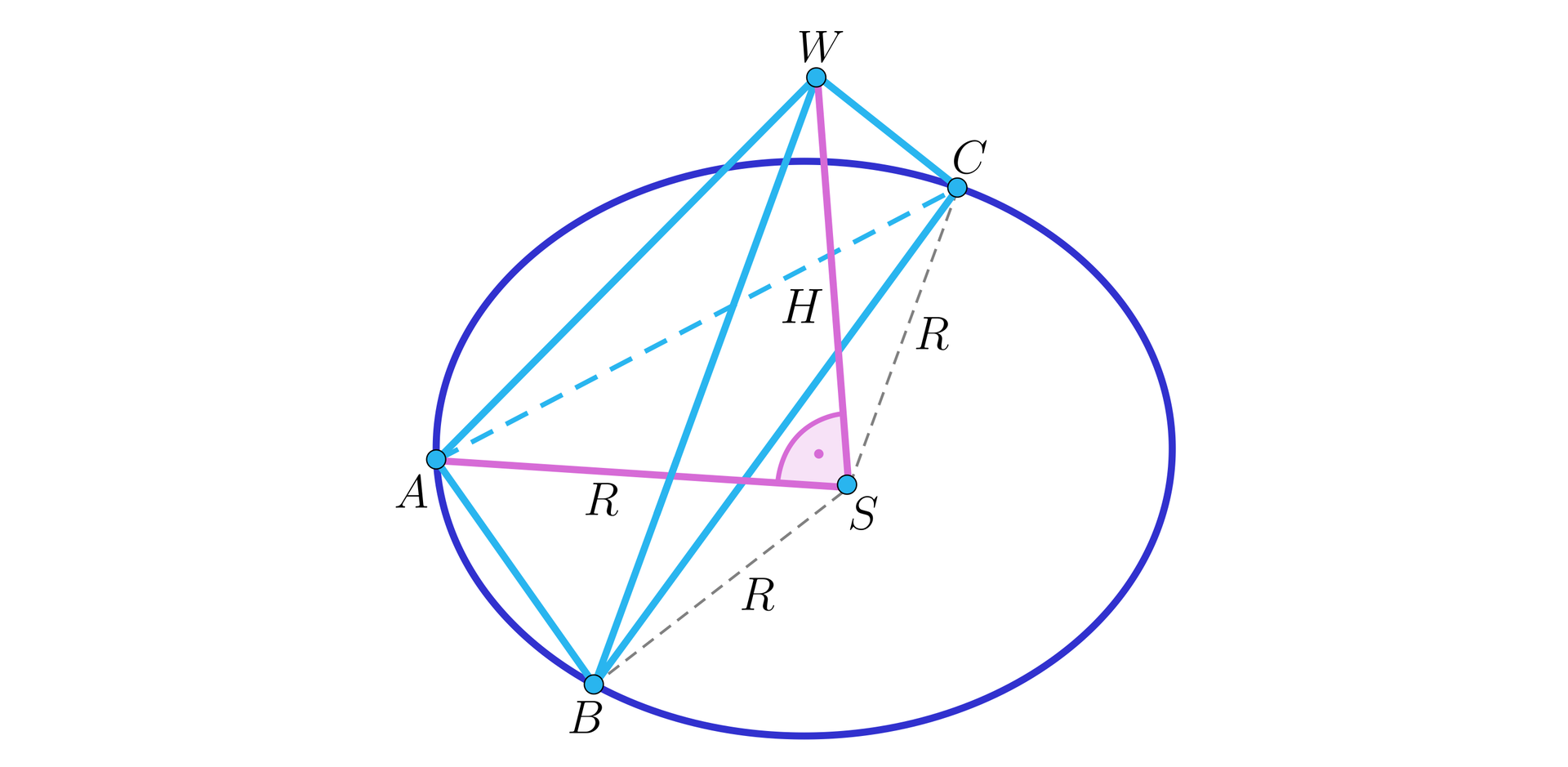
Aby obliczyć wysokość ostrosłupa, musimy obliczyć promień okręgu opisanego na jego podstawie. W tym celu wykorzystamy twierdzenie sinusówtwierdzenie sinusów dla trójkąta :
Teraz już bezpośrednio z twierdzenia Pitagorasa dla trójkąta możemy wyznaczyć wysokość ostrosłupa.
.
Rozważmy ostrosłup, którego podstawą jest romb niebędący kwadratem a spodek wysokości znajduje się w punkcie przecięcia przekątnych rombu. Pokażemy, że nie jest to ostrosłup prosty.
Rozwiązanie
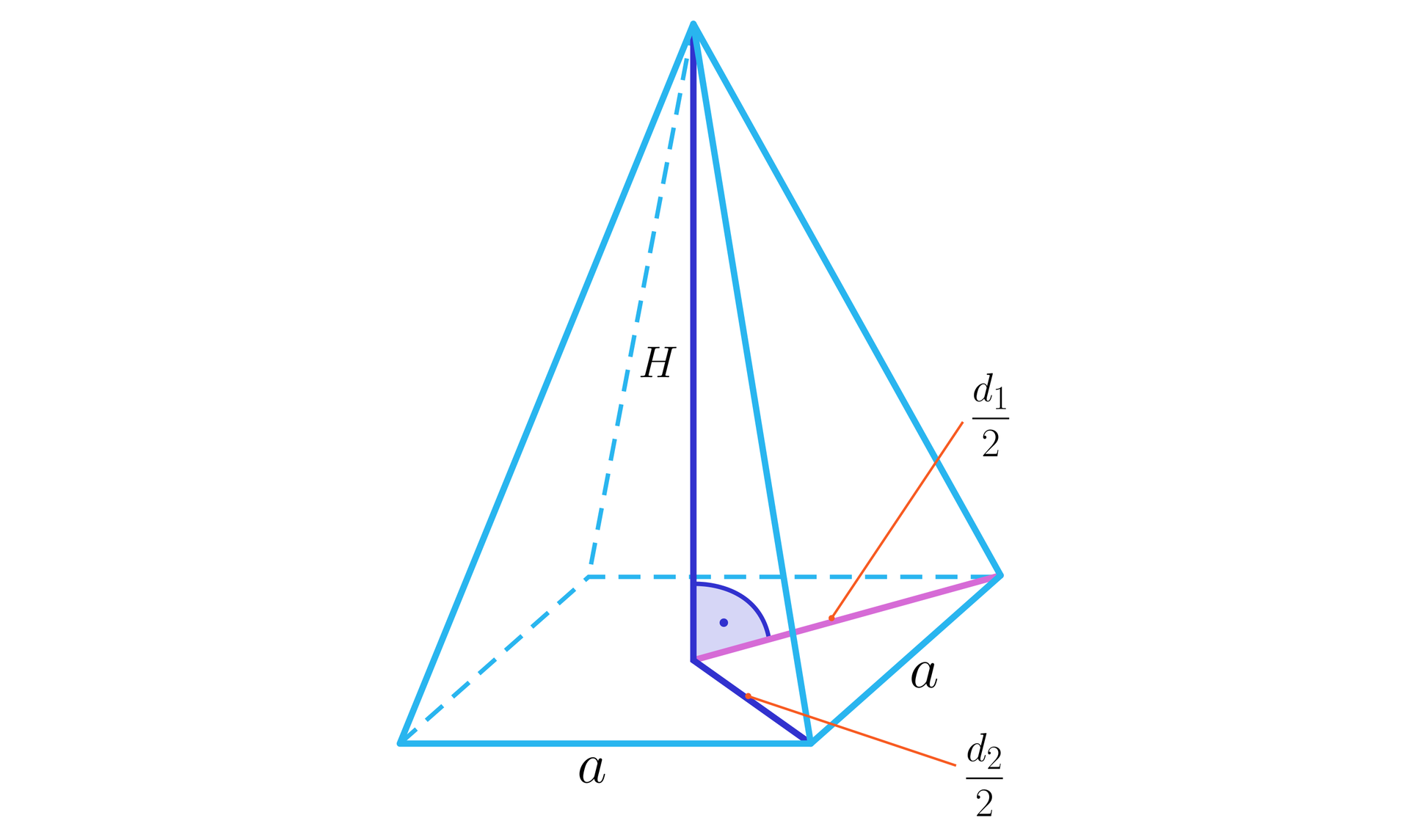
Niech i oznaczają przekątne rombu będącego podstawą ostrosłupa. Skoro nie jest on kwadratem, to . Rozważmy trójkąty prostokątne, w których jedną z przyprostokątnych jest wysokość ostrosłupa a drugą połowa przekątnej podstawy. Mamy więc różne trójkąty prostokątne o wspólnej przyprostokątnej, w których drugie przyprostokątne są różnej długości. Oznacza to, że przeciwprostokątne w tych trójkątach są różnej długości. Rozważane przeciwprostokątne są krawędziami bocznymi ostrosłupa. Skoro są one równej długości, to ostrosłup, którego podstawą jest romb nie jest ostrosłupem prostym.
Zwróć uwagę, że spodek wysokości ostrosłupa może nie znajdować się na podstawie ostrosłupa. Rozważmy ostrosłup pochyły:
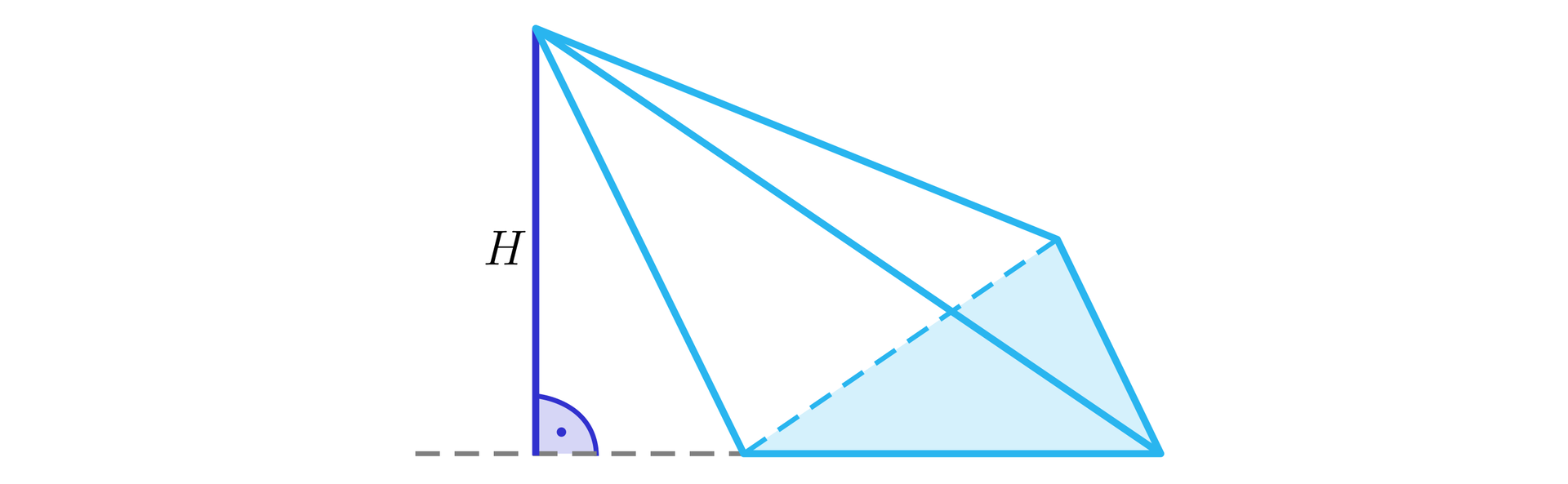
Zauważmy, że ostrosłup prosty nie zawsze w przestrzeni sprawia wrażenie „nie nachylonego”. Wszystko zależy od własności wielokąta z podstawy ostrosłupa. Jeżeli środek okręgu opisanego na takim wielokącie znajduje się poza wielokątem, to nasz ostrosłup musi „pochylać się” wierzchołkiem, w którym zbiegają się wszystkie jego krawędzie boczne. Rozpatrzmy zatem jeszcze mniejszy podzbiór ostrosłupów, czyli ostrosłupy prawidłowe.
Ostrosłupem prawidłowym nazywamy taki ostrosłup prosty, którego podstawa jest wielokątem foremnym.
Zauważmy, że ostrosłupy prawidłowe są bardzo regularne. Nie tylko podstawa takiego ostrosłupa jest wielokątem foremnymwielokątem foremnym, ale też wszystkie jego ściany boczne są identycznymi trójkątami równoramiennymi. W przypadku takich ostrosłupów często wykorzystujemy własności wielokątów foremnych. W szczególności fakt, że na każdym takim wielokącie da się opisać okrąg i do każdego takiego wielokąta można wpisać okrąg, a te dwa okręgi są współśrodkowe.
Różnica między polem okręgu opisanego na sześciokącie foremnym a polem okręgu wpisanego w ten sześciokąt wynosi . Sześciokąt jest podstawą ostrosłupa o wysokości . Znajdziemy długość krawędzi bocznej tego ostrosłupa.
Rozwiązanie
Spójrzmy na podstawę ostrosłupa
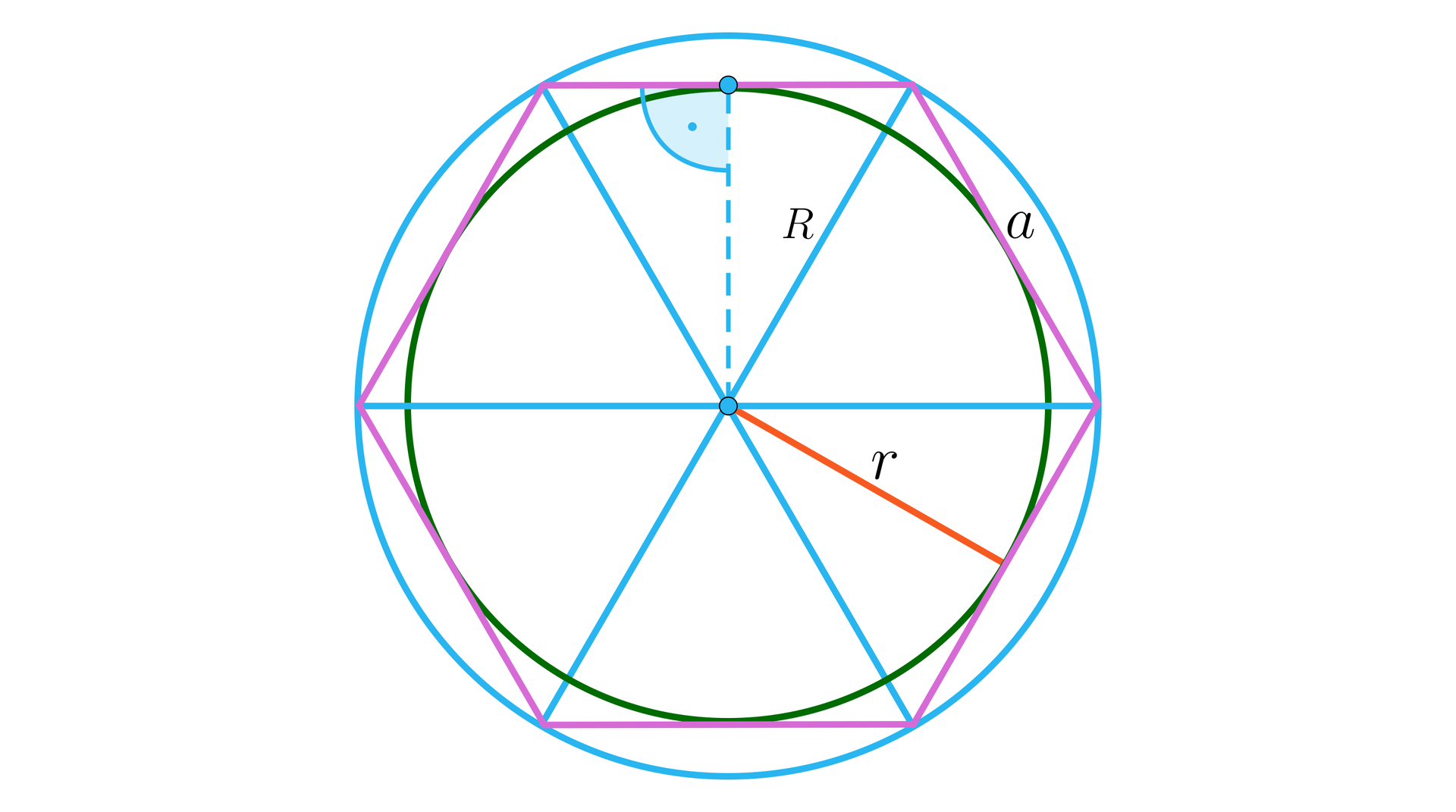
Z własności sześciokąta foremnego wiemy, że oraz . Mamy więc, że . Z treści zadania wiemy, że . Oznacza to, że krawędź podstawy ma długość . Zatem krawędź boczna ostrosłupa to przeciwprostokątna w trójkącie równoramiennym o przyprostokątnej . Krawędź boczna ma więc długość .
Słownik
jest to warunek konieczny i wystarczający na to, by na czworokącie można było opisać okrąg. Na czworokącie wypukłym można opisać w okrąg wtedy i tylko wtedy, gdy sumy miar kątów przeciwległych czworokąta są równe i wynoszą
twierdzenie określające warunki wystarczające, by trójkąty prostokątne były podobne; jeżeli dwa trójkąty prostokątne mają kąt ostry tej samej miary, to są do siebie podobne
twierdzenie pozwalające ustalić związek między bokami i kątami trójkąta oraz promieniem okręgu na nim opisanego. W dowolnym trójkącie stosunek długości jego boku do sinusa kąta leżącego na przeciw jest stały i równy średnicy okręgu opisanego na tym trójkącie
wielokąt, którego wszystkie boki są równej długości i wszystkie kąty wewnętrzne są równej miary
ostrosłup prawidłowy trójkątny, w którym wszystkie krawędzie mają tę samą długość