Przeczytaj
Algorytm Dijkstry – wprowadzenie
Algorytm Dijkstry służy do wyznaczania najkrótszych ścieżek w grafach skierowanych oraz nieskierowanych o dodatnich wagach. Jego zadaniem jest wyznaczenie najkrótszej ścieżkinajkrótszej ścieżki z wierzchołka początkowego do pozostałych osiągalnych wierzchołków.

Algorytm Dijkstry wykorzystuje podejście zachłanne.
Algorytmy zachłanne charakteryzują się tym, że dokonują wyboru, który jest najlepszy lokalnie, w nadziei na znalezienie najlepszego rozwiązania całego problemu.
Więcej na temat algorytmów zachłannych znajdziesz w e‑materiale Algorytmy zachłanneAlgorytmy zachłanne i pozostałych e‑materiałach z tej serii.
W kolejnych krokach wybierany jest (spośród tych wierzchołków, które nie zostały jeszcze odwiedzone) ten wierzchołek, do którego prowadzi najkrótsza ścieżka.
Algorytm Dijkstry może przydać ci się przy wyznaczaniu najkrótszej drogi do danego miejsca – w takim wypadku skrzyżowania to węzły grafu, a długości ulic – wagi krawędzi.
Wykorzystuje się go również w sieciach komputerowych, czego przykładem może być trasowanie (z ang. routing), które opisujemy w e‑materiale TrasowanieTrasowanie.
Zasada działania algorytmu
Przyjmijmy następujące założenia:
analizowany graf to graf spójnygraf spójny o dodatnich wagach;
wierzchołek
sto wierzchołek początkowy, od którego wyznaczane będą ścieżki do wszystkich pozostałych wierzchołków;zbiór
Vto zbiór wszystkich wierzchołków grafu;zbiór
Sbędzie zawierał wierzchołki, dla których długości ścieżekdługości ścieżek zostały już wyznaczone; na samym początku zbiórSjest pusty;tablica
d[], w której dla każdego wierzchołka przechowujemy wyznaczoną długość ścieżkid[u]z wierzchołka początkowegos;tablica
p[]jest tablicą poprzedników na najkrótszej ścieżce do wierzchołka początkowego.
Długość ścieżki prowadzącej do wierzchołka początkowego s wynosi 0 (d[s] = 0), a dla wszystkich pozostałych długość ta na początku jest równa ∞. W implementacji zwykle jako nieskończoność przyjmuje się wystarczająco dużą liczbę, co do której mamy pewność, że jest większa niż wartość długości jakiejkolwiek ścieżki – z tego powodu może być też to liczba, która jest większa od liczby wierzchołków pomnożonych przez najdłuższą krawędź grafu.
Oznaczenie w(u,v) przyjmujemy za wagę krawędzi uv.
Lista kroków algorytmu:
Tworzymy dwa zbiory wierzchołków –
VorazS.Dla wszystkich wierzchołków grafu (oznaczonych jako
u) za wyjątkiem początkowego (oznaczonego jakos) ustawiamy długość ścieżek (czyli elementów tablicyd) na nieskończoność.Wartość
d[s]ustawiamy na 0.Ustawiamy poprzednik każdego wierzchołka (elementy tablicy
p) jako niezdefiniowany (możemy użyć np. wartości -1).Dopóki zbiór
Vnie jest pusty:Wybieramy ze zbioru
Vwierzchołek u o najmniejszym koszcie dojścia do niego (d[u]).Wybrany wierzchołek
uusuwamy ze zbioruVi dodajemy do zbioruS.Dla każdego sąsiada wierzchołka
u(oznaczonego jakov)sprawdzamy, czyd[v] > d[u] + w(u,v).Jeśli
d[v] > d[u] + w(u,v), wyznaczamy nową długość ścieżki do wierzchołkavoraz wierzchołekuzostaje poprzednikiem wierzchołkav.Jeśli nie, nic się nie dzieje.
Przykład wykorzystania
Zastosujmy algorytm Dijkstry dla przykładowego grafu w celu wyznaczenia najkrótszych ścieżek z wierzchołka A do wszystkich pozostałych.
Oto przykładowy graf:
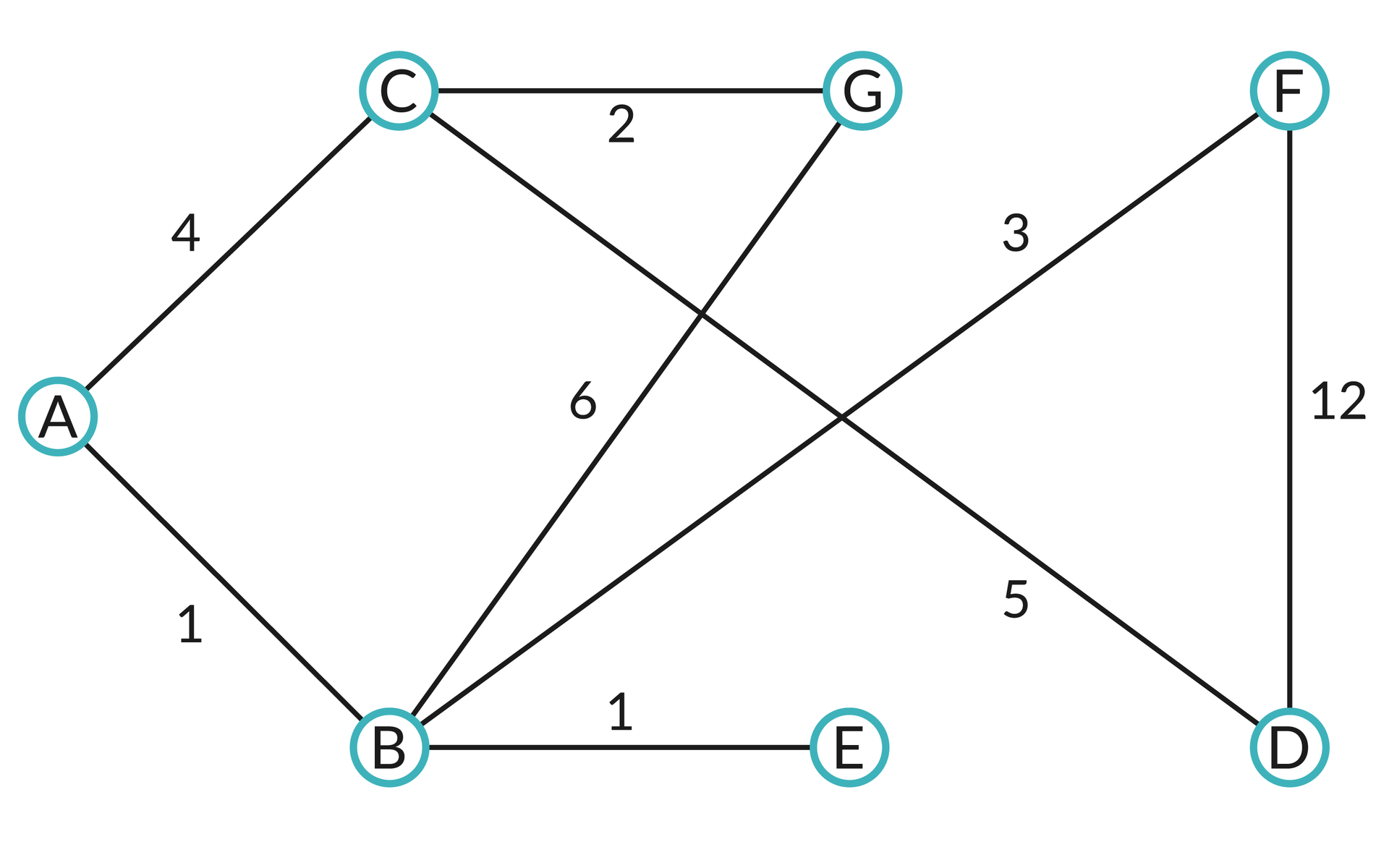
Jak już zostało wskazane, wierzchołkiem początkowym jest wierzchołek A.
Naszym zadaniem jest wyznaczenie najkrótszych ścieżek prowadzących z wierzchołka początkowego A do wszystkich pozostałych wierzchołków oraz najkrótszych ścieżek pomiędzy wierzchołkiem początkowym a wszystkimi pozostałymi.
Tworzymy dwa zbiory.
Zbiór S początkowo jest pusty.
Zbiór V zawiera wszystkie wierzchołki zbioru
Tworzymy dwie n-elementowe tablice: d oraz p. Liczba n to liczba wierzchołków grafu.
Tablica d przechowuje długości najkrótszych ścieżek do poszczególnych wierzchołków z wierzchołka początkowego.
Tablica p przechowuje informację na temat poprzedników na ścieżce do danego wierzchołka.
Utwórzmy tabelę, w której będziemy aktualizować stan poszczególnych ścieżek.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| |||||||
|
Uzupełniamy początkowy stan tabeli zgodnie z krokami 2–4 algorytmu.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| -1 | -1 | -1 | -1 | -1 | -1 | -1 |
W zbiorze V szukamy wierzchołka u o najmniejszym koszcie dojścia do niego (d[u]). To początek wykonywania algorytmu, zatem jest to wierzchołek początkowy, którego d[u] = 0 (ponieważ jest to wierzchołek A, to d[A] = 0). Długości ścieżek do pozostałych wierzchołków są większe.
Wierzchołek przenosimy zatem ze zbioru V do S. Przeglądamy wszystkich sąsiadów przeniesionego wierzchołka. To wierzchołki C oraz B.
Sprawdzamy warunek:
Jest prawdziwy, ponieważ suma 0 oraz 1 jest mniejsza od nieskończoności, zatem:
W konsekwencji uzupełniamy pierwszą komórkę tabeli i do p[B] wpisujemy A, czyli poprzednik na ścieżce, a do d[B] wpisujemy 1, czyli długość ścieżki.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ∞ | ∞ | ∞ | ∞ | ∞ |
| -1 | A | -1 | -1 | -1 | -1 | -1 |
Analogicznie postępujemy dla wierzchołka C.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | ∞ | ∞ | ∞ | ∞ |
| -1 | A | A | -1 | -1 | -1 | -1 |
Stan zbiorów:
Ponownie ze zbioru V wybieramy wierzchołek u o najniższym koszcie dojścia do niego (d[u]).
Tym razem jest to wierzchołek B. Przenosimy go do zbioru S i sprawdzamy jego sąsiadów.
Sprawdzamy warunki.
Patrząc od góry, pierwszy warunek nie jest spełniony, ponieważ zero jest mniejsze od 2, zatem przechodzimy dalej.
Pozostałe warunki są spełnione – nieskończoność jest większa od 2, 4 oraz 7.
Zatem:
Uzupełniamy tabelę.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | ∞ | 2 | 4 | 7 |
| -1 | A | A | -1 | B | B | B |
Stan zbiorów:
Kolejnym wierzchołkiem w zbiorze V, do którego ścieżka (d[u]) jest najkrótsza, jest wierzchołek E.
Przenosimy go do zbioru S i sprawdzamy jego sąsiadów oraz odpowiednie warunki.
Nie, zatem nic się nie zmienia.
Stan zbiorów:
Kolejnym wierzchołkiem w zbiorze V, do którego ścieżka (d[u]) jest najkrótsza, jest wierzchołek C.
Przenosimy go do zbioru S i sprawdzamy jego sąsiadów oraz odpowiednie warunki.
Uzupełniamy tabelę. Zwróć uwagę, że zmieniamy wcześniej wpisaną wartość.
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | 9 | 2 | 4 | 6 |
| -1 | A | A | C | B | B | C |
Stan zbiorów:
Kolejnym wierzchołkiem w zbiorze V, do którego ścieżka (d[u]) jest najkrótsza, jest wierzchołek G.
Przenosimy go do zbioru S i sprawdzamy jego sąsiadów oraz odpowiednie warunki.
W tabeli nic się nie zmienia.
Stan zbiorów:
Kolejnym wierzchołkiem w zbiorze V, do którego ścieżka (d[u]) jest najkrótsza, jest wierzchołek D.
Przenosimy go do zbioru S i sprawdzamy jego sąsiadów oraz odpowiednie warunki.
W tabeli nic się nie zmienia.
Stan zbiorów:
Ostatnim wierzchołkiem w zbiorze V jest wierzchołek F.
Przenosimy go do zbioru S i sprawdzamy jego sąsiadów oraz odpowiednie warunki.
W tabeli nic się nie zmienia.
Uzupełniona tabela prezentuje się następująco:
| A/p> | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | 9 | 2 | 4 | 6 |
| -1 | A | A | C | B | B | C |
Algorytm Dijkstry nazywamy zachłannym, ponieważ na każdym etapie dokonuje wyboru lokalnie najkorzystniejszego z nadzieją znalezienia rozwiązania globalnie optymalnego. Taką decyzją jest wybranie wierzchołka o najmniejszym koszcie, a następnie dodanie go do zbioru S.
Zastosowanie algorytmów zachłannych nie zawsze gwarantuje uzyskanie najlepszych możliwych wyników. W przypadku algorytmu Dijkstry rzeczywiście tak jest – odnajdujemy najkrótsze ścieżki.
Słownik
suma wag wszystkich krawędzi, z których składa się ścieżka, droga lub cykl
struktura składająca się z niepustego zbioru wierzchołków oraz rodziny krawędzi; dla grafu G zbiór wierzchołków oznaczamy (ang. verticies – wierzchołki), a rodzinę krawędzi – (ang. edges – krawędzie); liczbę elementów zbioru oznaczamy literą ; liczbę elementów rodziny –
graf, w którym każda para wierzchołków połączona jest drogą
graf którego krawędzie mają przypisane wagi
taka ścieżka łącząca dwa wierzchołki grafu, której suma wag krawędzi jest jak najmniejsza
nieuporządkowana para (niekoniecznie różnych) elementów zbioru wierzchołków
relacja między wierzchołkami a łączącą je krawędzią grafu; mówimy, że dwa sąsiednie wierzchołki połączone pewną krawędzią są incydentne z tą krawędzią
właściwość grafów polegająca na tym, że między grafami występuje wzajemnie jednoznaczna odpowiedniość wierzchołków; liczba krawędzi łączących dane dwa wierzchołki jednego grafu jest równa liczbie krawędzi łączących odpowiadające im wierzchołki drugiego grafu
zestaw uporządkowanych list, gdzie lista o indeksie jest listą wszystkich sąsiadów wierzchołka
dwuwymiarowa tablica elementów (zwykle liczbowych), licząca wierszy i kolumn
macierz zerojedynkowa rozmiaru , dla której każda krawędź grafu musi mieć unikatowy indeks; wyraz jest równy , o ile krawędź o indeksie jest incydentna do wierzchołka
macierz zerojedynkowa rozmiaru , w której wyraz jest równy , jeśli wierzchołki oraz są sąsiednie, a w przeciwnym przypadku; macierz sąsiedztwa jest symetryczna dla grafów nieskierowanych
liczba krawędzi incydentnych z danym wierzchołkiem
klasa lub interfejs sparametryzowany względem typów podanych przy deklaracji; do określenia parametrów typu używamy nawiasów ostrych (<>); typy generyczne umożliwiają napisanie ogólnej definicji, która działa z różnymi typami, pozwalając tym samym na ponowne użycie kodu bez konieczności definiowania nowych definicji klas lub interfejsu działających na innym typie zmiennych
wartość przypisana krawędzi grafu
element należący do zbioru wierzchołków