Przeczytaj
W zbiorze liczb całkowitych mamy zdefiniowane dzielenie z resztą.
Wiemy, że przy dzieleniu liczby przez liczbę możemy uzyskać całkowity iloraz oraz resztę , przy czym reszta jest liczbą całkowitą taką, że .
Zachodzi wtedy równość .
Wielomian jest podzielny przez niezerowy wielomian wtedy i tylko wtedy, gdy istnieje wielomian taki, że .
Obliczymy sposobem pisemnym iloraz wielomianów oraz .
-

Zastosowany zapis przypomina dzielenie pisemne liczb naturalnych. Zapiszmy oba wielomiany i narysujmy poziomą linię nad pierwszym z nich.
-
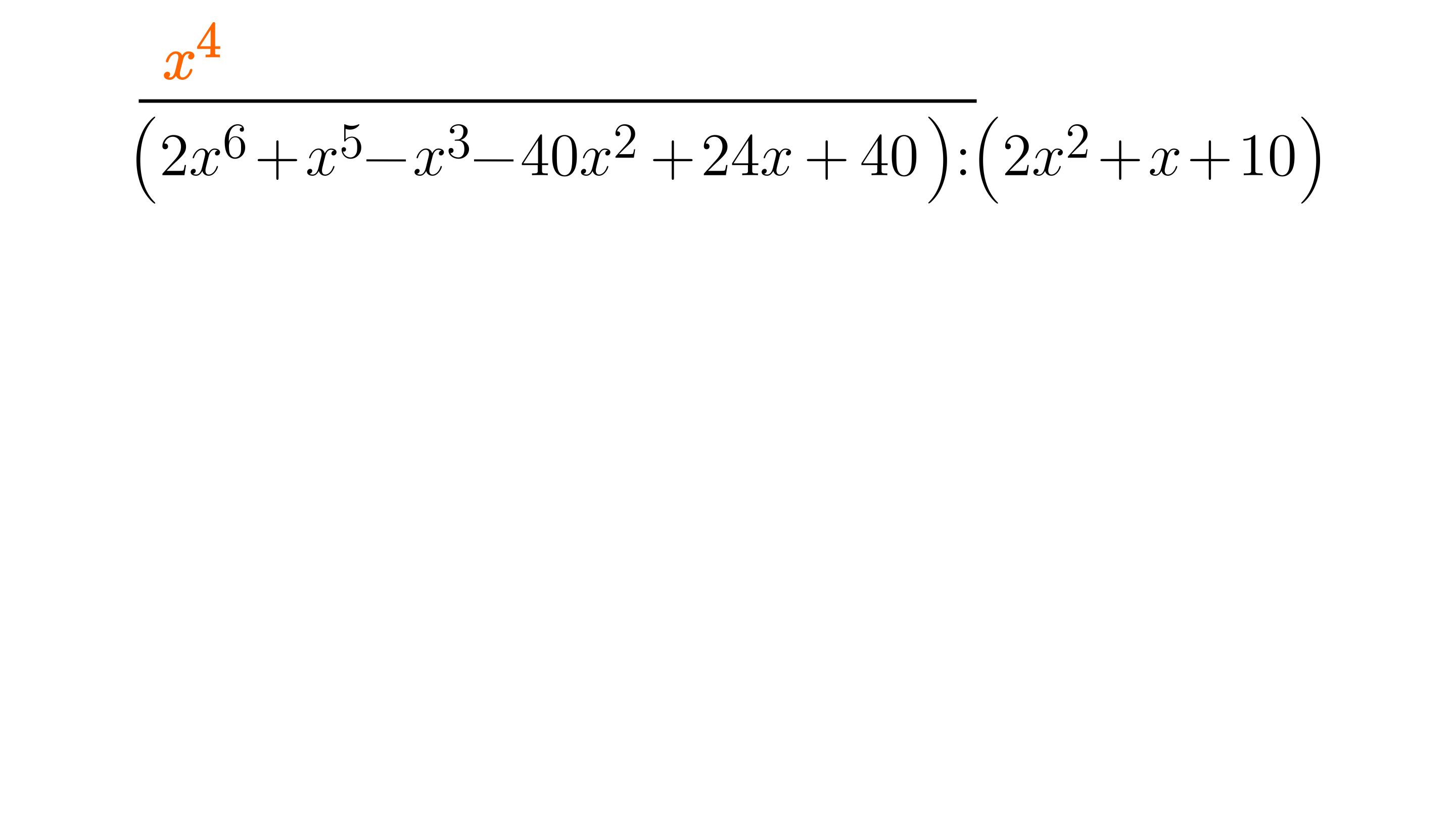
Podzielmy pierwsze wyrazy obu wielomianów: . Uzyskany wynik zapiszmy nad pierwszym wyrazem pierwszego wielomianu.
-

Obliczmy iloczyn zapisanego wyrażenia przez drugi wielomian:
. Uzyskany wynik zapiszmy pod pierwszym wielomianem dopisując znak odejmowania. -

Wykonajmy odejmowanie. Wynik zapiszmy pod kreską. Nie trzeba zapisywać wszystkich wyrazów różnicy, wystarczy o jeden więcej niż stopień wielomianu, przez który dzielimy.
-
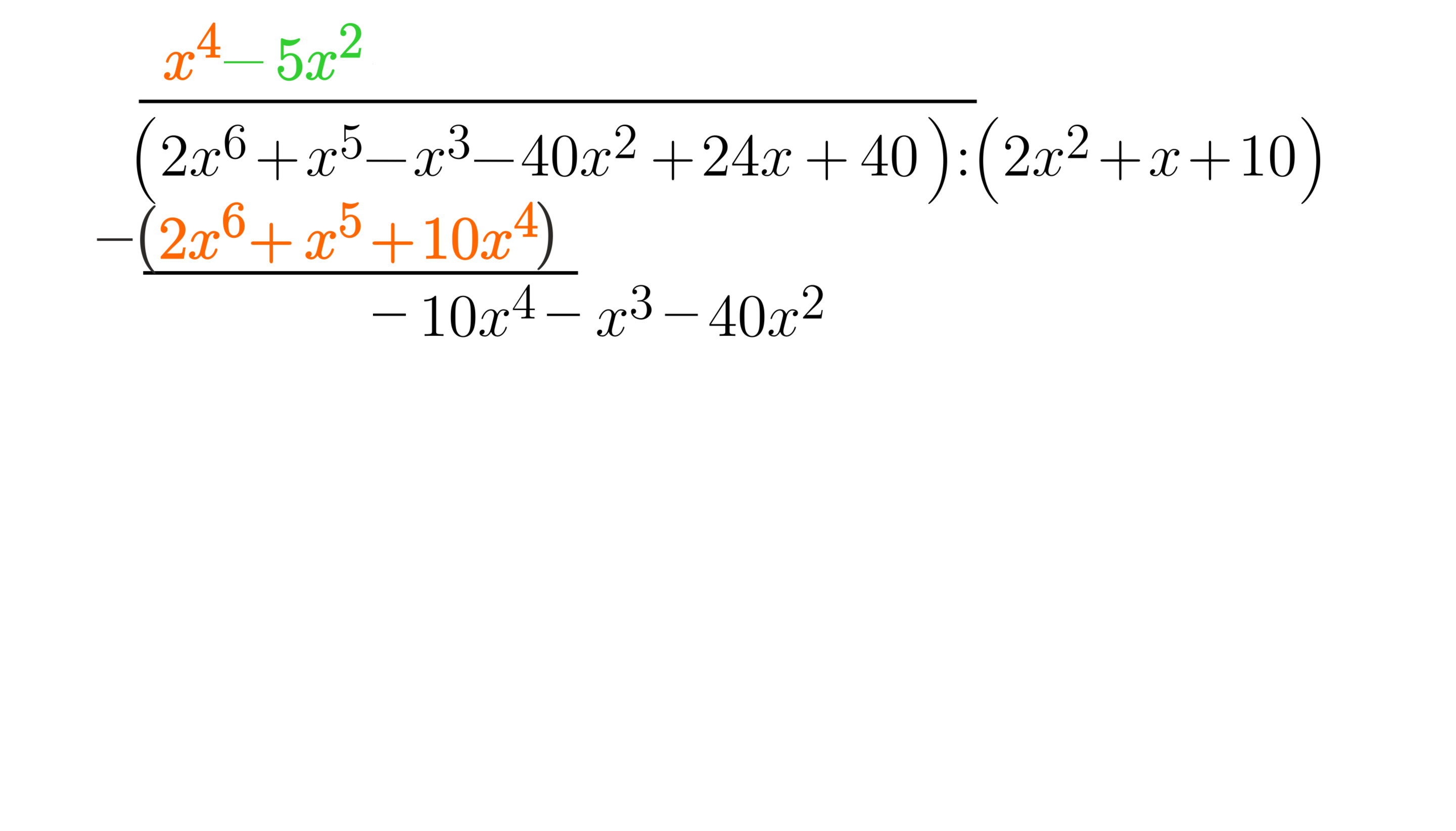
Podzielmy pierwszy wyraz uzyskanej różnicy przez pierwszy wyraz wielomianu, przez który dzielimy:. Dodajemy uzyskany wynik do zapisu nad kreską.
-

Teraz podobnie jak poprzednio obliczymy iloczyn wyniku ostatniego dzielenia przez drugi wielomian: . Uzyskany wynik analogicznie dopisujemy ze znakiem minus.
-
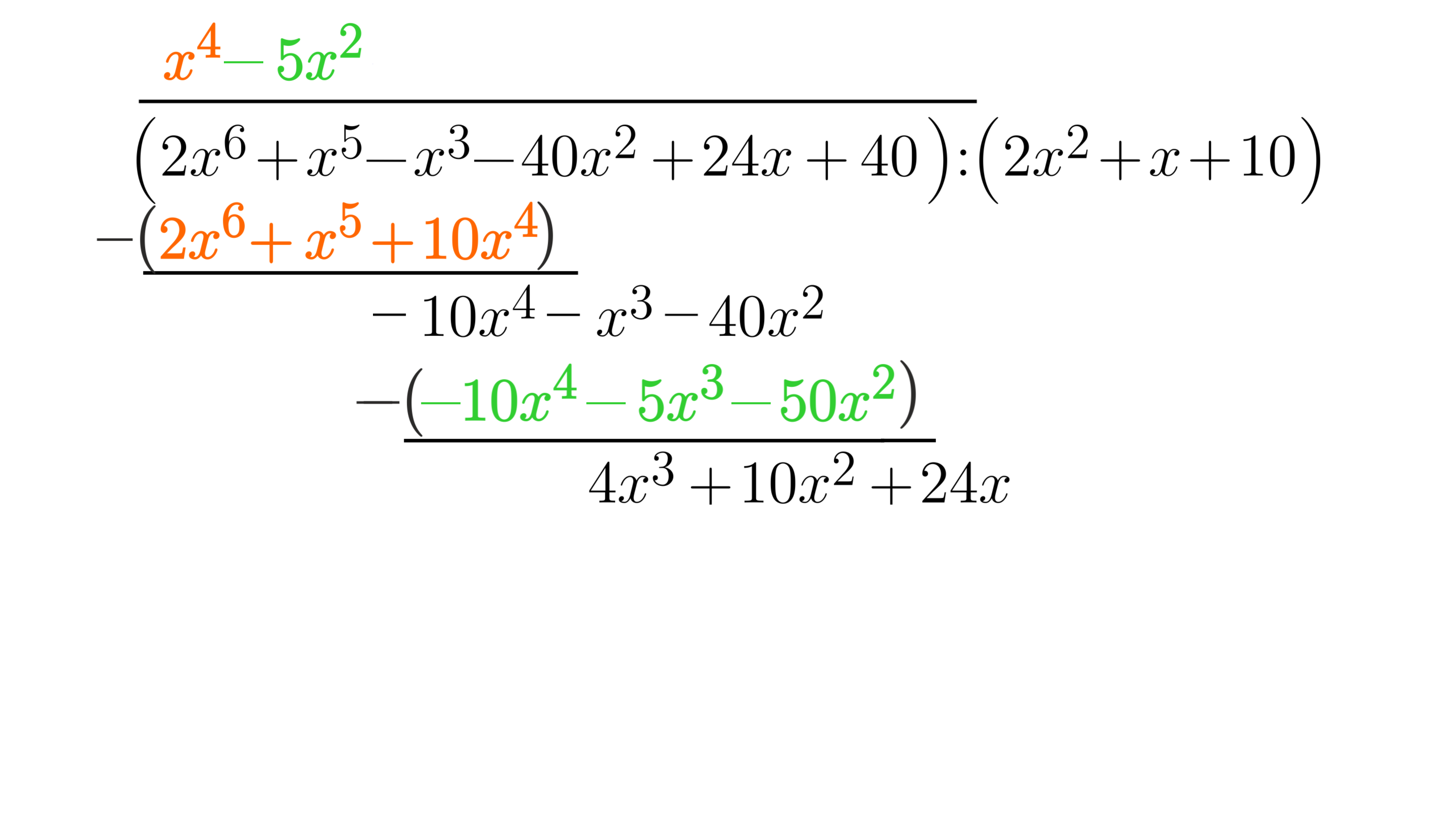
Podobnie jak wcześniej wykonujemy odejmowanie, uzupełniając wynik składnikami pierwszego wielomianu.
-
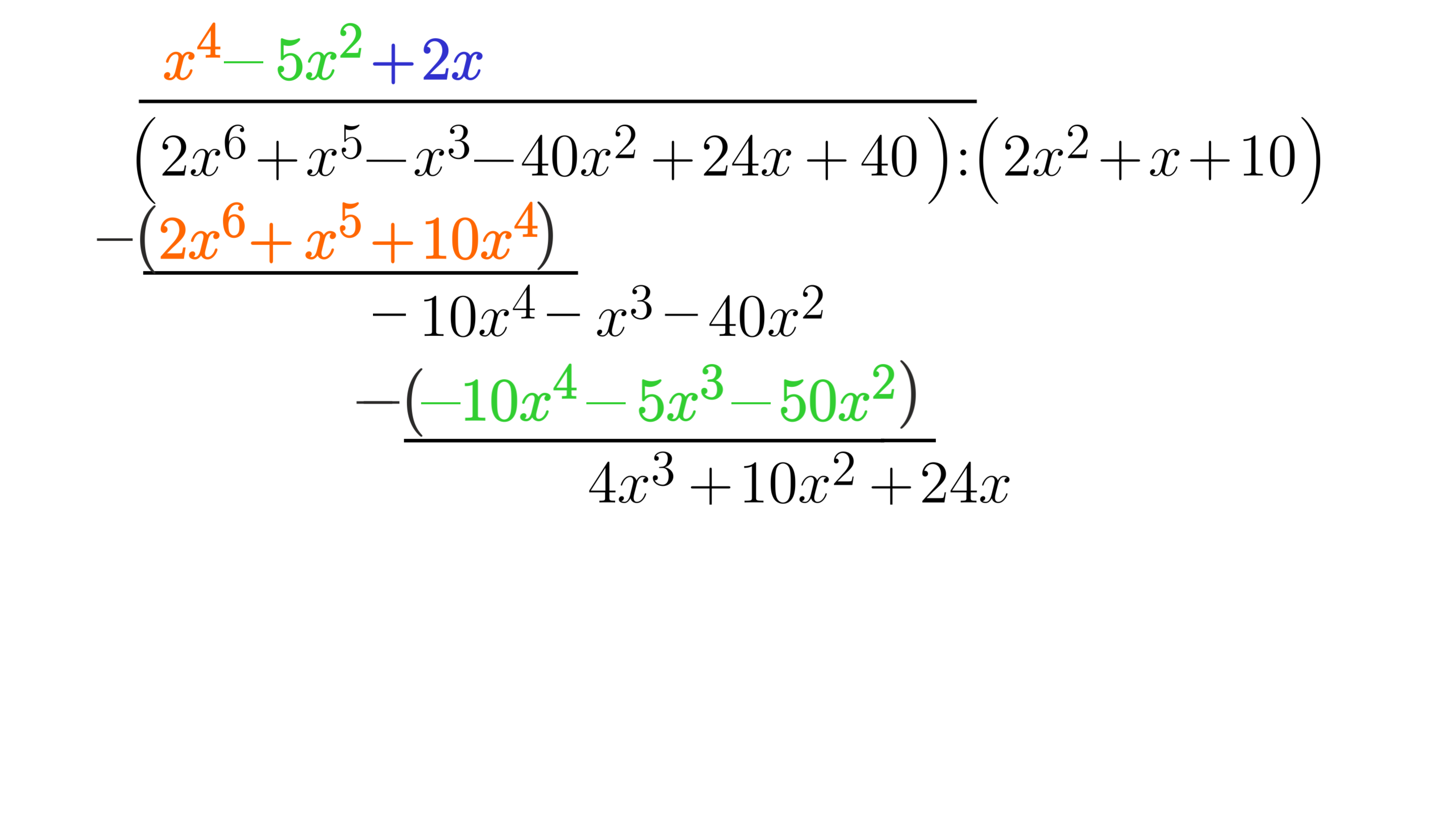
Powtarzamy cały schemat, dopóki stopień wielomianu uzyskanego po odejmowaniu nie jest mniejszy od stopnia wielomianu, przez który dzielimy.
-
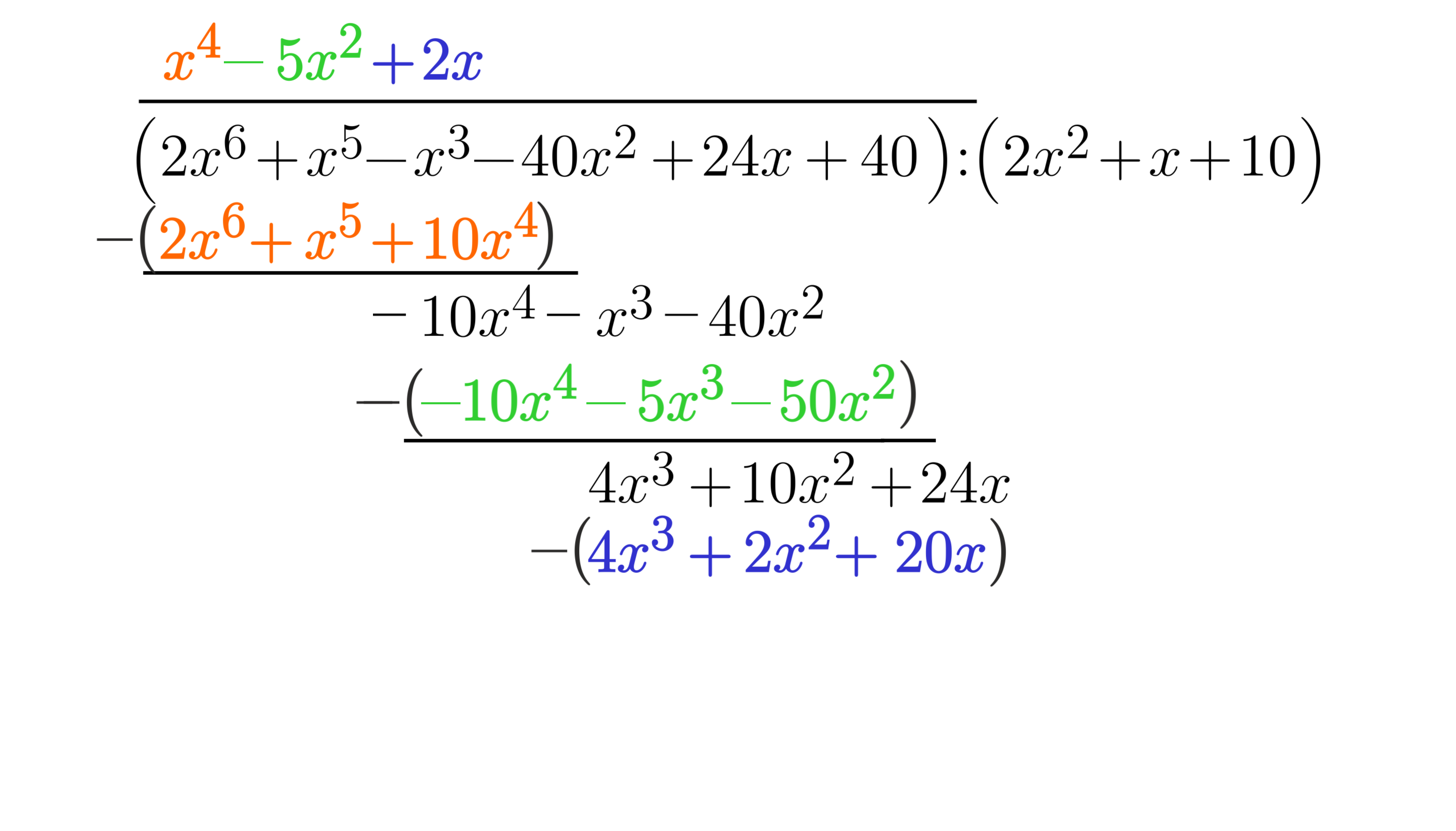
-

-
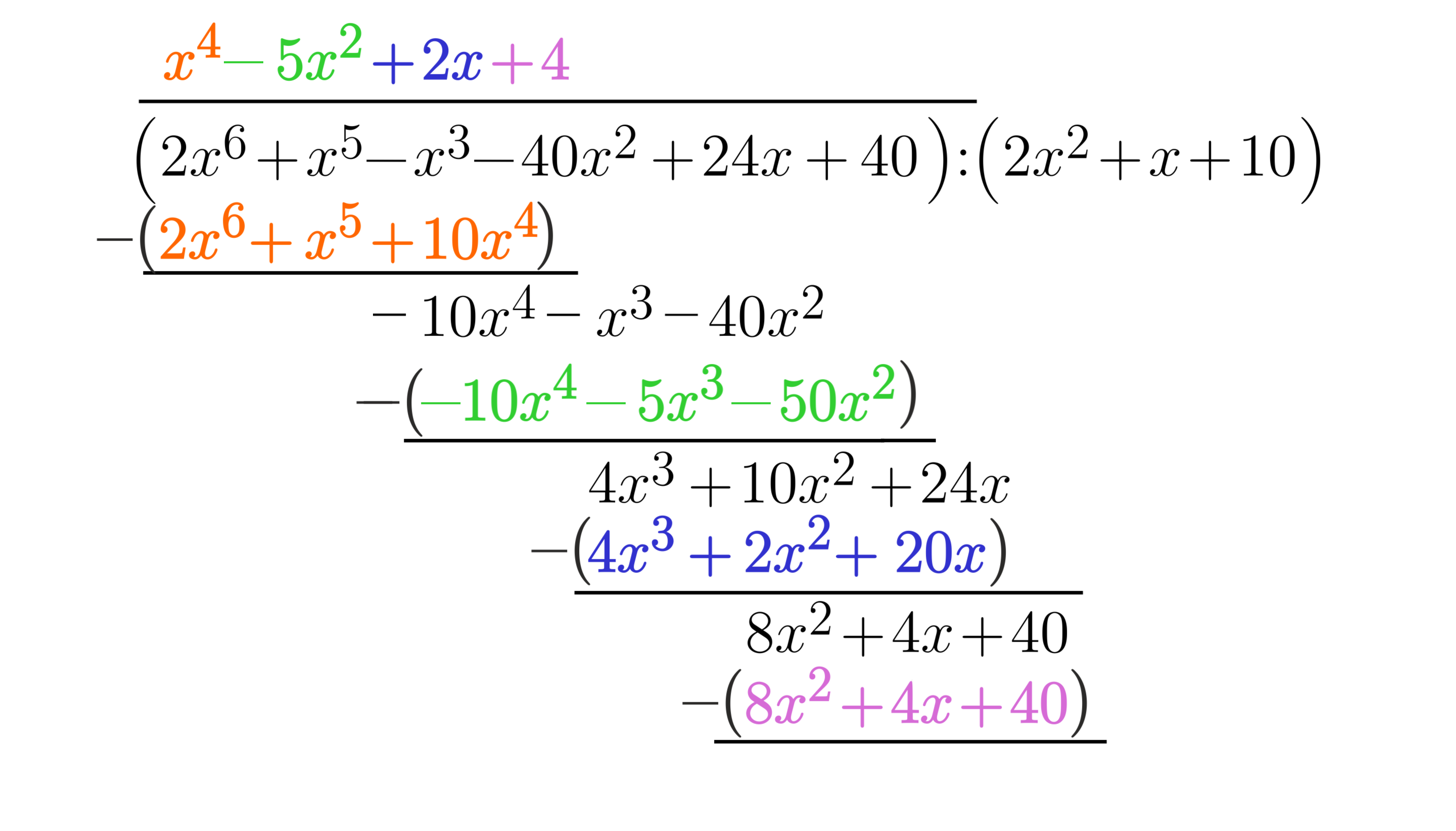
-
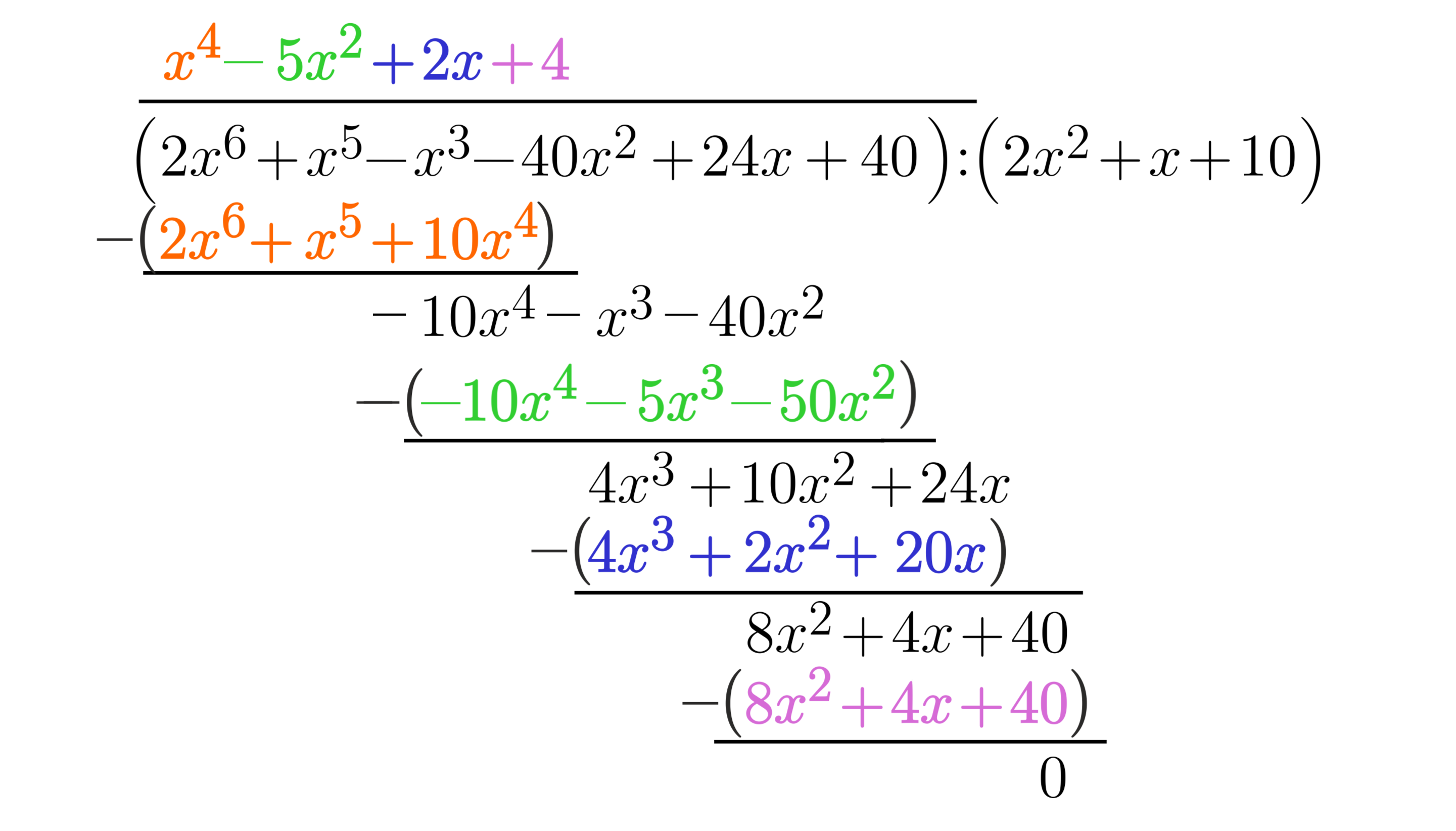
Jeżeli uzyskana różnica będzie stopnia mniejszego niż wielomian, przez który dzielimy lub będzie wielomianem zerowym, kończymy wykonywanie algorytmu.
Wielomian zapisany u góry nad kreską jest ilorazem.
Jeśli ostatnia uzyskana różnica jest wielomianem zerowym (jak w podanym przykładzie), to pierwszy wielomian jest podzielny przez drugi wielomian. W przeciwnym wypadku uzyskana różnica jest resztą z dzielenia.
Etapy dzielenia.
Zastosowany zapis przypomina dzielenie pisemne liczb naturalnych. Zapiszmy oba wielomiany i narysujmy poziomą linię nad pierwszym z nich.
Podzielmy pierwsze wyrazy obu wielomianów: . Uzyskany wynik zapiszmy nad pierwszym wyrazem pierwszego wielomianu.
Obliczmy iloczyn zapisanego wyrażenia przez drugi wielomian:
. Uzyskany wynik zapiszmy pod pierwszym wielomianem dopisując znak odejmowania, czyli .Wykonajmy odejmowanie. Wynik zapiszmy pod kreską. Wynosi on . Nie trzeba zapisywać wszystkich wyrazów różnicy, wystarczy o jeden więcej niż stopień wielomianu, przez który dzielimy. Otrzymujemy więc wielomian: .
Podzielmy pierwszy wyraz uzyskanej różnicy przez pierwszy wyraz wielomianu, przez który dzielimy:. Dodajemy uzyskany wynik do zapisu nad kreską.
Teraz podobnie jak poprzednio obliczymy iloczyn wyniku ostatniego dzielenia przez drugi wielomian: . Uzyskany wynik analogicznie dopisujemy ze znakiem minus.
Podobnie jak wcześniej wykonujemy odejmowanie, uzupełniając wynik składnikami pierwszego wielomianu. Mamy więc odejmowanie pisemne. Od wielomianu odejmujemy wielomian . Wynikiem odejmowania wielomianów jest . Następnie dopisujemy do tego wielomianu .
Powtarzamy cały schemat, dopóki stopień wielomianu uzyskanego po odejmowaniu nie jest mniejszy od stopnia wielomianu, przez który dzielimy.
Jeżeli uzyskana różnica będzie stopnia mniejszego niż wielomian, przez który dzielimy lub będzie wielomianem zerowym, kończymy wykonywanie algorytmu.
Jednomian dzielimy przez pierwszy jednomian dzielnika, czyli przez . Otrzymujemy , zatem dopisujemy w wierszu wynikowym i mnożymy jednomian przez wielomian będący dzielnikiem. Poniżej zapisujemy iloczyn ze zmienionym znakiem, czyli .
Dodajemy do siebie te wielomiany. Pod kreską zapisujemy wynik: . Dopisujemy do niego ostatni jednomian wielomianu , czyli .
Jednomian dzielimy przez pierwszy jednomian dzielnika , czyli . Otrzymany wynik zapisujemy w wierszu wynikowym jako i mnożymy przez ten jednomian dzielnik . Poniżej w wierszu zapisujemy iloczyn ze zmienionym znakiem, czyli .
Dodajemy do siebie dwa otrzymane wielomiany i pod kreską zapisujemy wynik, który wynosi .
Wielomian zapisany u góry nad kreską jest ilorazem. Wynosi on .
Uwaga! Jeśli ostatnia uzyskana różnica jest wielomianem zerowym (jak w podanym przykładzie), to pierwszy wielomian jest podzielny przez drugi wielomian. W przeciwnym wypadku uzyskana różnica jest resztą z dzielenia.
Pokażemy, jak podzielićpodzielić wielomian przez wielomian sposobem pisemnym.
Metoda dzielenia w pewnym stopniu przypomina sposób, w jaki pisemnie dzielimy dwie liczby całkowite.
Po ułożeniu puzzli zobaczysz, jak można zapisywać takie dzielenie.
Kolejne etapy dzielenia pisemnego wielomianów.
Zapisujemy wielomian wu od x dzielony przez wielomian P od x.
Pierwszy jednomian z wielomianu wu dzielimy kolejno przez pierwszy jednomian wielomianu P i wynik zapisujemy nad górną poziomą kreską oddzielającą wynik główny od dzielenia pisemnego.
Następnie mnożymy jednomian wyniku głównego przez kolejne składniki dzielnika czyli wielomianu pe od x i zapisujemy je z przeciwnym znakiem pod dzielną, czyli pod wielomianem wu od x.
Odkreślamy poziomą kreską i dodajemy pisemnie oba nowe wielomiany. Wynik tego działania zapisujemy pod kreską.
Przepisujemy po prawej stronie wyniku dodawania nowo powstałych wielomianów, kolejne pozostałe jednomiany dzielnej wu od x, ale nie wszystkie, tylko tyle, żeby nowa dzielna i dzielnik składały się z takiej samej liczby jednomianów.
Pierwszy jednomian tego wyniku jest naszą nową dzielną, którą dzielimy przez pierwszy jednomian wielomianu p od x.
Powtarzamy schemat od punktu drugiego, aż otrzymamy wynik dzielenia całego wielomianu.
Dzielenie w kolejnych etapach na podanym przykładzie.
Dzielna to wielomian wu postaci dwa x do potęgi szóstej dodać x do potęgi piątej odjąć siedemnaście x do potęgi czwartej odjąć x do sześcianu dodać 45 x kwadrat odjąć 10 x odjąć dwadzieścia osiem.
Dzielnik to wielomian p od x postaci: dwa x kwadrat dodać x odjąć siedem.
Kolejne etapy dzielenia na przykładzie wymienimy poniżej w kolejnych punktach.
Bierzemy pierwszy jednomian wielomianu wu od x, czyli jednomian postaci 2 x do potęgi szóstej i dzielimy go po kolei przez jednomiany składowe wielomianu pe od x. Nad kreską wyniku głównego zapisujemy x do potęgi czwartej, ponieważ 2 x do potęgi szóstej podzielić na 2 x kwadrat równa się x do potęgi czwartej.
Następnie pod wielomianem wu od x zapisujemy minus 2 x do potęgi szóstej i dzielimy kolejne iloczyny jednomianu x do potęgi czwartej z pozostałymi jednomianami dzielnika. Czyli mamy drugi jednomian: x do potęgi czwartej razy x równa się x do potęgi piątej oraz x do potęgi czwartej razy minus siedem równa się minus 7 x do potęgo czwartej. Zatem pod wielomianem wu od x mamy wielomian minus 2 x do potęgi szóstej odjąć x do potęgi piątej dodać siedem x. Oddzielamy kreską pionową kolejny wiersz i zapisujemy pod kreską sumę. Potęgi szóste i piąte redukują się, więc wynikiem jest jednomian minus 10 x do potęgi czwartej.
Powtarzamy schemat. Przez jednomian minus 10 x do potęgi czwartej dzielimy pierwszy jednomian wielomianu p od x. To daje minus 5 x kwadrat. Wynik ten zapisujemy jako drugi jednomian wyniku głównego. Następnie zapisujemy za jednomianem minus 10 x do potęgi czwartej dwa kolejne jednomiany wielomiany wu od x, czyli minus x do sześcianu dodać 45 x kwadrat. W kolejnym wierszu zapisujemy iloczyny jednomianu minus 5 x kwadrat wielomianu p od x, ale z przeciwnym znakiem. Mamy więc 10 x do potęgi czwartej dodać 5 x do sześcianu odjąć 35 x kwadrat. Po dodaniu wielomianów w obu wierszach, otrzymujemy wielomian: x do sześcianu dodać 10 x kwadrat.
Przepisujemy za nowym wynikiem kolejny jednomian wielomianu wu od x, czyli minus 10 x. Ponawiamy schemat. Naszą nową dzielną jest jednomian 4 x do sześcianu. Dzielimy ten jednomian przez 2 x kwadrat, otrzymując 2 x. Zapisujemy wynik dalej nad kreską wynikową. Przepisujemy ostatni jednomian wielomianu wu od x, czyli minus 10 x. Mnożymy kolejne jednomiany dzielnika przez 2 x i zapisujemy iloczyny ze zmienionym znakiem w wierszu poniżej. Mamy więc minus 4 x do sześcianu odjąć 2 x kwadrat dodać 14 x. Pod wielomianem wykreślamy poziomą kreskę oddzielającą. Dodajemy oba wielomiany.
Trzecie potęgi się redukują, więc wynikiem dodawania jest wielomian 8 x kwadrat dodać 4 x i przepisujemy ostatni już jednomian wielomianu wu od x, czyli minus dwadzieścia osiem. Naszą nową dzielną jest 8 x kwadrat, którą dzielimy przez 2 x kwadrat. Zapisujemy w wierszu wynikowym iloraz cztery. Mnożymy teraz przez 4 wielomian p od x. Iloczyn zapisujemy w kolejnym wierszu, ale ze zmienionym znakiem. Mamy więc: minus 8 x kwadrat odjąć 4 x dodać 28, a po dodaniu tych dwóch wielomianów otrzymujemy zero. Zatem wynik to x do potęgi czwartej odjąć 5 x kwadrat dodać 2 x dodać cztery.
A co w sytuacji, gdy dla danego wielomianu i niezerowego wielomianu nie istnieje wielomian taki, że ?
Dla każdego wielomianu i niezerowego wielomianu istnieją wielomiany i takie, że , przy czym wielomian , nazywany resztą z dzielenia, jest stopnia mniejszego niż stopień wielomianu lub jest wielomianem zerowym.
Wykonamy dzielenie: .
Rozwiązanie
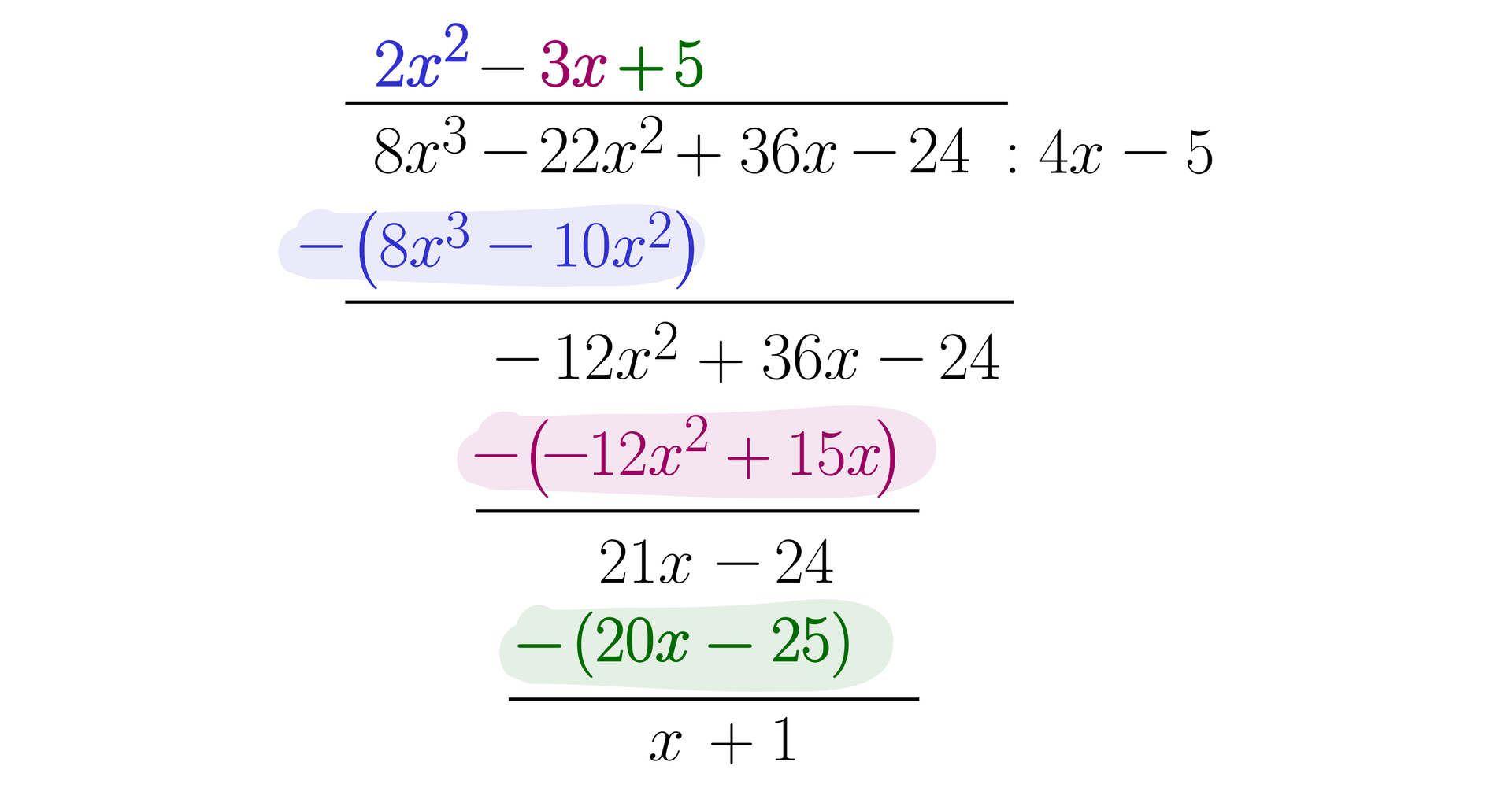
Wielomian zapiszemy zatem w postaci:
Dwumian jest resztą z dzielenia wielomianu przez trójmian .
Resztą z dzielenia pewnego wielomianu przez wielomian jest wielomian stopnia zerowego , a resztą z dzielenia przez jest .
Wyznaczymy wielomian, który jest resztą z dzielenia przez .
Rozwiązanie
Wiadomo, że .
Ponadto reszta z dzieleniadzielenia przez wielomian stopnia drugiego jest wielomianem stopnia co najwyżej pierwszego lub wielomianem zerowym, czyli można ją zapisać w postaci .
Zatem
Zauważmy, że z pierwszej równości wiadomo, że
zaś z drugiej
.
Wykorzystajmy to w trzeciej równości:
,
czyli .
Rozwiązując ten układ równań uzyskujemy i , czyli .
Wyznaczymy takie wartości parametrów i , dla których reszta z dzielenia wielomianu przez wielomian jest równa .
Film dostępny pod adresem https://zpe.gov.pl/a/D1NA4xHnC
Film nawiązujący do treści materiału dotyczącej dzielenia wielomianów.
Słownik
dla każdego wielomianu i niezerowego wielomianu istnieją wielomiany i takie, że , przy czym wielomian nazywany resztą z dzielenia jest stopnia mniejszego niż stopień wielomianu lub jest wielomianem zerowym
wielomian jest podzielny przez niezerowy wielomian wtedy i tylko wtedy, gdy istnieje wielomian taki, że