Dane są dwa niepuste zbiory $X$ i $Y$.

Funkcją $f$ ze zbioru $X$ w zbiór $Y$ nazywamy przyporządkowanie, które każdemu elementowi $x$ ze zbioru $X$ przyporządkowuje dokładnie jeden element $y$ ze zbioru $Y$.

FunkcjafunkcjaFunkcja $f$ opisana jest słownie.

Funkcja $f$ każdej liczbie naturalnej $x$ takiej, że $x\in ⟨27, 39⟩$ przyporządkowuje jej największy dzielnik, który jest liczbą pierwszą.

Rozwiązanie:

Z opisu funkcji możemy odczytać, że dziedziną tej funkcji są liczby naturalne należące do przedziału $⟨27, 39⟩$.

Symbolicznie możemy zapisać $D_f=\left\{27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39\right\}$.

Funkcja $f$ opisana jest za pomocą grafu.

R1EkratbXSlAy

Ilustracja przedstawia funkcje f opisaną za pomocą grafu. Zbiór x zawiera liczby: minus 4, minus 2, 0, 1, 2, $3\frac{1}{2}$. Zbiór y zawiera liczby: minus 1, 0, minus 1; Liczby z obu zborów są połączone w następujący sposób: minus 4 z minus 1, minus 2 z minus 1, 0 z 0, 1 z minus 1, 2 z minus 1 i  $3\frac{1}{2}$ z minus .

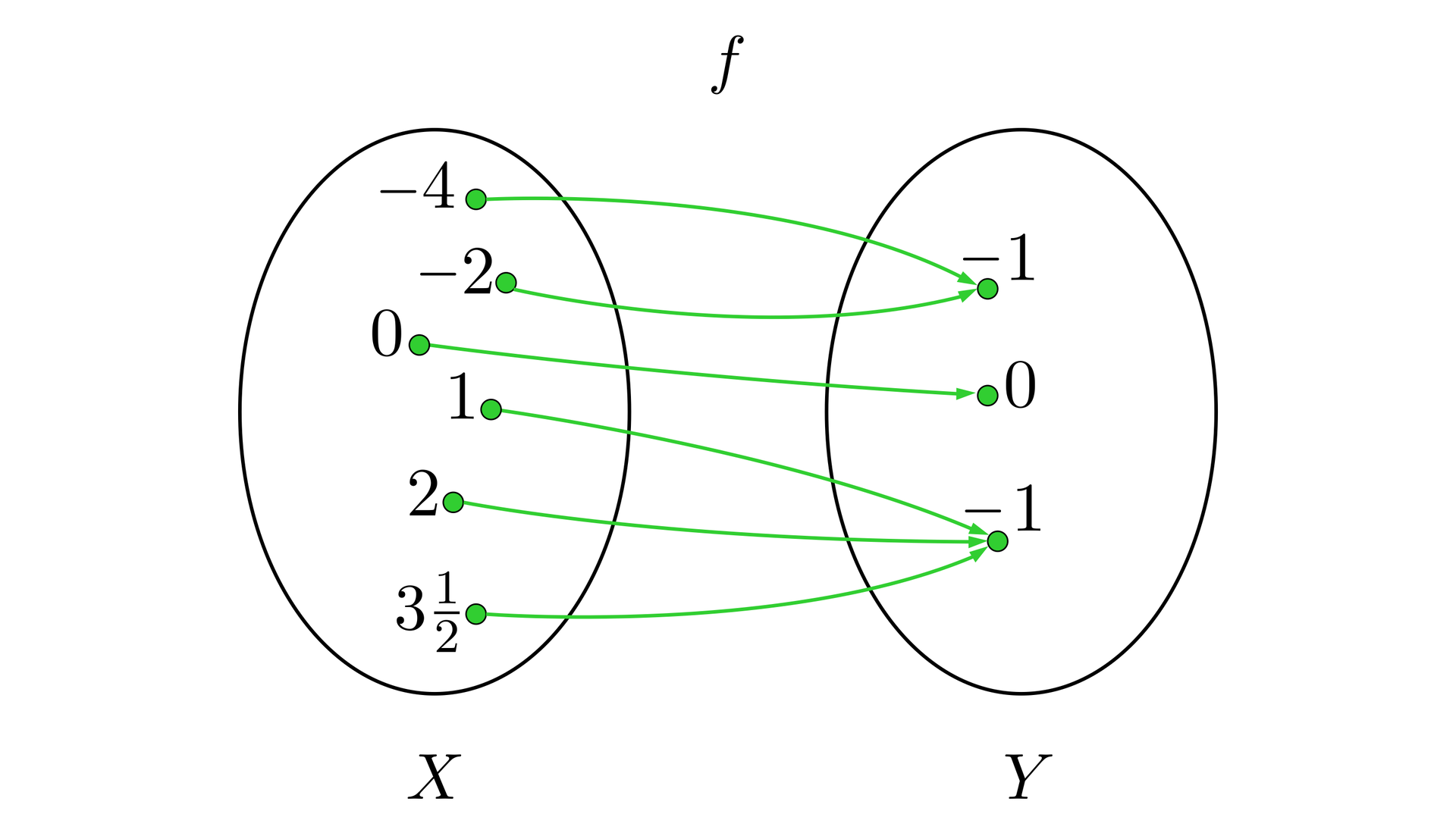
Rozwiązanie:

Analizując graf odczytujemy dziedzinę funkcji.

Do dziedziny funkcji należą elementy umieszczone w lewej części grafu.

Stąd $D_f=\left\{-4, -2, 0, 1, 2, 3\frac{1}{2}\right\}$.

Funkcja $f$ opisana jest za pomocą tabelki.

Rozwiązanie:

Do dziedziny funkcji należą liczby zapisane w pierwszym wierszu tabelki.

Stąd $D_f=\left\{-3\sqrt{3}, -2\sqrt{2}, -1, 0, \sqrt{2}, 3, 2\sqrt{5}, 6, 8\sqrt{2}\right\}$.

Funkcja $f$ opisana jest za pomocą zbioru par uporządkowanych.

$\left\{\left(-4\frac{2}{3}, -2\right),\left(-3\frac{3}{7}, -4\right),\left(-\frac{2}{9}, -\frac{4}{11}\right),\left(-1, -\frac{5}{6}\right),\left(2\frac{3}{4}, 5\right),\left(3\frac{3}{8}, 6\frac{4}{5}\right),\left(4, 7\frac{3}{5}\right),\left(6\frac{1}{5}, 8\frac{4}{7}\right)\right\}$

Rozwiązanie:

Każda para uporządkowana jest postaci $\left(x, f\left(x\right)\right)$.

Dziedzinę funkcji tworzą wszystkie liczby, które są umieszczone na pierwszym miejscu w każdej parze.

Stąd $D_f=\left\{-4\frac{2}{3},-3\frac{3}{7},-\frac{2}{9},-1,2\frac{3}{4},3\frac{3}{8},4,6\frac{1}{5}\right\}$.

Funkcja $f$ opisana jest za pomocą wykresu.

RvX2LlwUN5MZk

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus pięciu do pięciu i pionową osią y od minus trzech do trzech. Na osi x  oznaczono zbiór od minus 5,5 do cztery . Przy czym punkt minus 5,5 jest zaznaczony zamalowaną kropką, a punkt 4 jest zaznaczony niezamalowaną kropką. W układzie narysowano wykres funkcji składający się z dwóch krzywych. Pierwsza jest łamaną składającą się z dwóch ukośnych odcinków. Pierwszy o końcach w zamalowanych punktach nawias minus pięć i pół średnik minus trzy zamkniecie nawiasu i w punkcie nawias minus jeden średnik jeden zamknięcie nawiasu. Drugi odcinek ma lewy koniec w zamalowanym punkcie nawias minus jeden średnik jeden zamknięcie nawiasu i z prawej strony jest ograniczony niezamalowanym punktem nawias dwa średnik dwa zamknięcie nawiasu. Drugą składową wykresu jest obcięta parabola o ramionach skierowanych do góry i wierzchołku w zamalowanym punkcie nawias trzy średnik minus trzy zamknięcie nawiasu. Lewe ramię obcięte jest w zamalowanym punkcie nawias dwa średnik jeden zamknięcie nawiasu, prawe ramię obcięte jest w niezamalowanym punkcie nawias cztery średnik jeden zamknięcie nawiasu.

Rozwiązanie:

Wiadomo, że wykres funkcji w prostokątnym układzie współrzędnych, to zbiór wszystkich punktów płaszczyzny o współrzędnych $\left(x, f\left(x\right)\right)$, gdzie $x$ jest argumentem funkcji, a $f\left(x\right)$ wartością funkcji dla argumentu $x$.

W celu odczytania z wykresu funkcji dziedziny tej funkcji należy odczytać wszystkie pierwsze współrzędne punktów wykresu.

Wyobraźmy sobie, że wszystkie pierwsze współrzędne punktów wykresu rzutujemy prostopadle na oś $X$. Na osi $X$ tworzy nam się zbiór wszystkich argumentów funkcji $f$, czyli dziedzina funkcji.

W przypadku narysowanego wykresu otrzymujemy $D_f=\left.⟨-\mathrm{5,5}; 4\right)$.

Rozpatrzymy następujące funkcje opisane wzorami. Określimy dziedzinę każdej z tych funkcji.

a) $f\left(x\right)=-2x+5$

b) $f\left(x\right)=\sqrt{x+3}$

c) $f\left(x\right)=\frac{x^3}{x-4}$

d) $f\left(x\right)=\frac{5}{\sqrt{x-6}}$

Rozwiązanie:

Ad. a)

W zbiorze liczb rzeczywistych wykonalne jest mnożenie i dodawanie, tzn., każdą liczbę rzeczywistą możemy pomnożyć przez $\left(-2\right)$ oraz do wyniku dodać liczbę pięć. Wynik tego działania też będzie liczbą rzeczywistą. Stąd wnioskujemy, że dziedziną funkcji $\left(x\right)=-2x+5$ jest zbiór liczb rzeczywistych i zapisujemy $D_f=\mathrm{ℝ}$.

Ad. b)

Pierwiastek kwadratowy możemy obliczyć tylko wtedy, gdy liczba podpierwiastkowa jest liczbą rzeczywistą nieujemną. Wynika z tego, że wartość funkcji $f$ możemy obliczyć wtedy, gdy spełniona jest nierówność

$x+3\ge 0$, czyli wtedy, gdy $x\ge -3$.

Dziedziną funkcji $f\left(x\right)=\sqrt{x+3}$ jest przedział $\left.⟨-3, \infty \right)$.

Zapisujemy, że $D_f=\left.⟨-3, \infty \right)$.

Ad. c)

Dowolną liczbę rzeczywistą można podnieść do sześcianu, od każdej liczby rzeczywistej można odjąć liczbę cztery, dzielenie sześcianu liczby rzeczywistej przez $x-4$ jest możliwe tylko wtedy, gdy $x-4\ne 0$. W zbiorze liczb rzeczywistych dzielenie przez $0$ jest niewykonalne.

Otrzymujemy: $x\ne 4$.

Dziedziną funkcji $\left(x\right)=\frac{x^3}{x-4}$ jest zbiór $\mathrm{ℝ}\setminus \left\{4\right\}$, czyli $D_f=\mathrm{ℝ}\setminus \left\{4\right\}$.

Ad. d)

Określając dziedzinę tej funkcji należy uwzględnić objaśnienia z poprzednich podpunktów, tzn. $x-6\ge 0$ i $x-6\ne 0$.

Warunki te można zastąpić jedną nierównością: $x-6>0$.

Stąd wynika, że $x>6$, czyli $D_f=\left(6, \infty \right)$.

funkcją $f$ ze zbioru $X$ w zbiór $Y$ nazywamy przyporządkowanie, w którym każdemu elementowi $x$ ze zbioru $X$ odpowiada dokładnie jeden element $y$ ze zbioru $Y$