W przestrzeni rozważamy trzy podstawowe obiekty: punkt, prostą, płaszczyznę. Przez dowolne dwa punkty można poprowadzić dokładnie jedną prostą. Przez dowolne trzy niewspółliniowe punkty można poprowadzić dokładnie jedną płaszczyznę. Problemy geometrii przestrzennej dają się często rozwiązać jako problemy planimetrii dzięki odpowiedniemu wyborowi płaszczyzny lub przekroju płaszczyzną.

Na płaszczyźnie proste, które nie mają punktów wspólnych są równoległe. W przestrzeni proste, które nie mają punktów wspólnych są równoległe tylko wtedy, gdy leżą na jednej płaszczyźnie. Istnieją w przestrzeni proste, które nie mają punktów wspólnych i nie są równoległe. Wszystkie takie proste nazywamy skośnymi.

Przykład 1

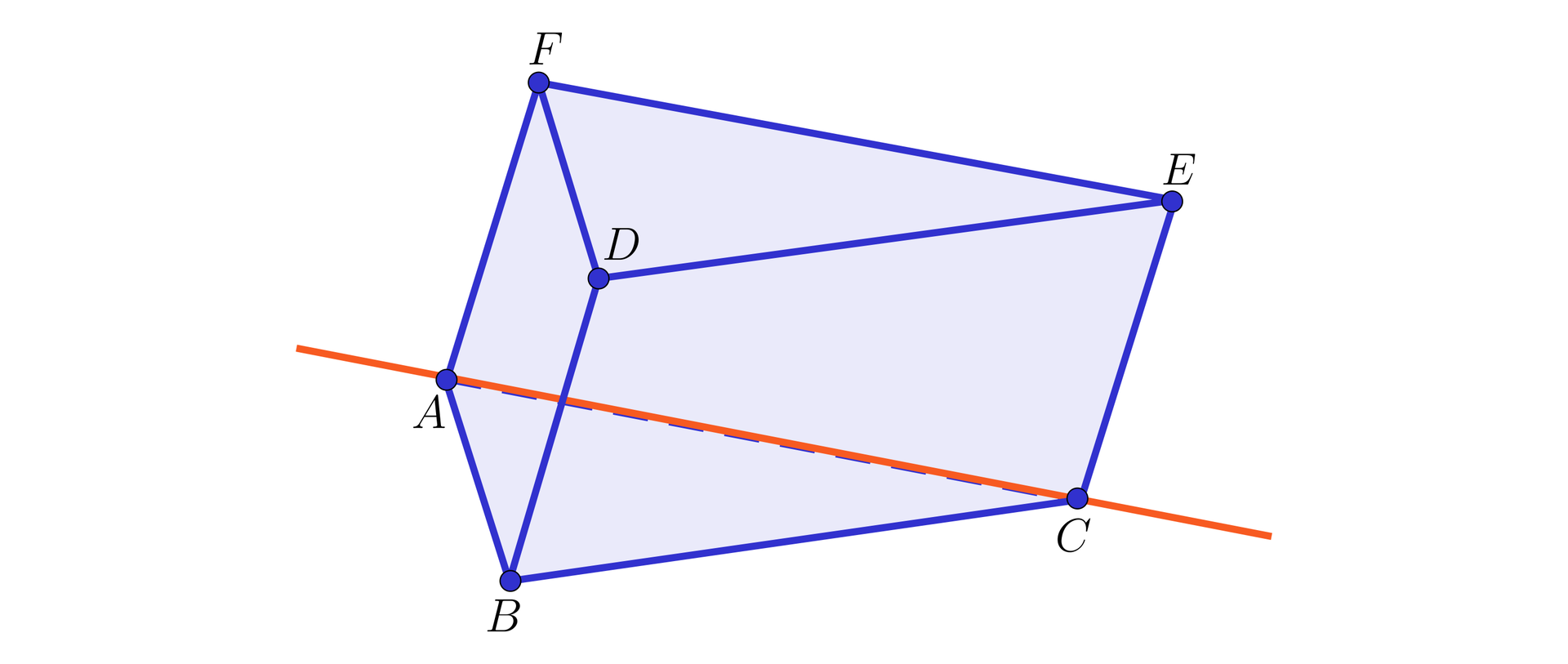
Na rysunku przedstawiony jest graniastosłup trójkątny. Sprawdzimy, które spośród prostych zawierających krawędzie tego graniastosłupa są skośne do prostej $AC$.

RnugGoCcJTXfn

Ilustracja przedstawia graniastosłup trójkątny A B C D E F, gdzie wierzchołek D znajduje się nad B, wierzchołek E nad C, wierzchołek F nad A. Przez krawędź A C poprowadzona została prosta.

Rozwiązanie

Proste $AF$, $AB$, $BC$ i $CE$ mają punkt wspólny z prostą $AC$.

Prosta $EF$ jest równoległa do $AC$.

Pozostają trzy proste skośne z $AC$, a mianowicie $DB$, $DE$ i $DF$.

Przykład 2

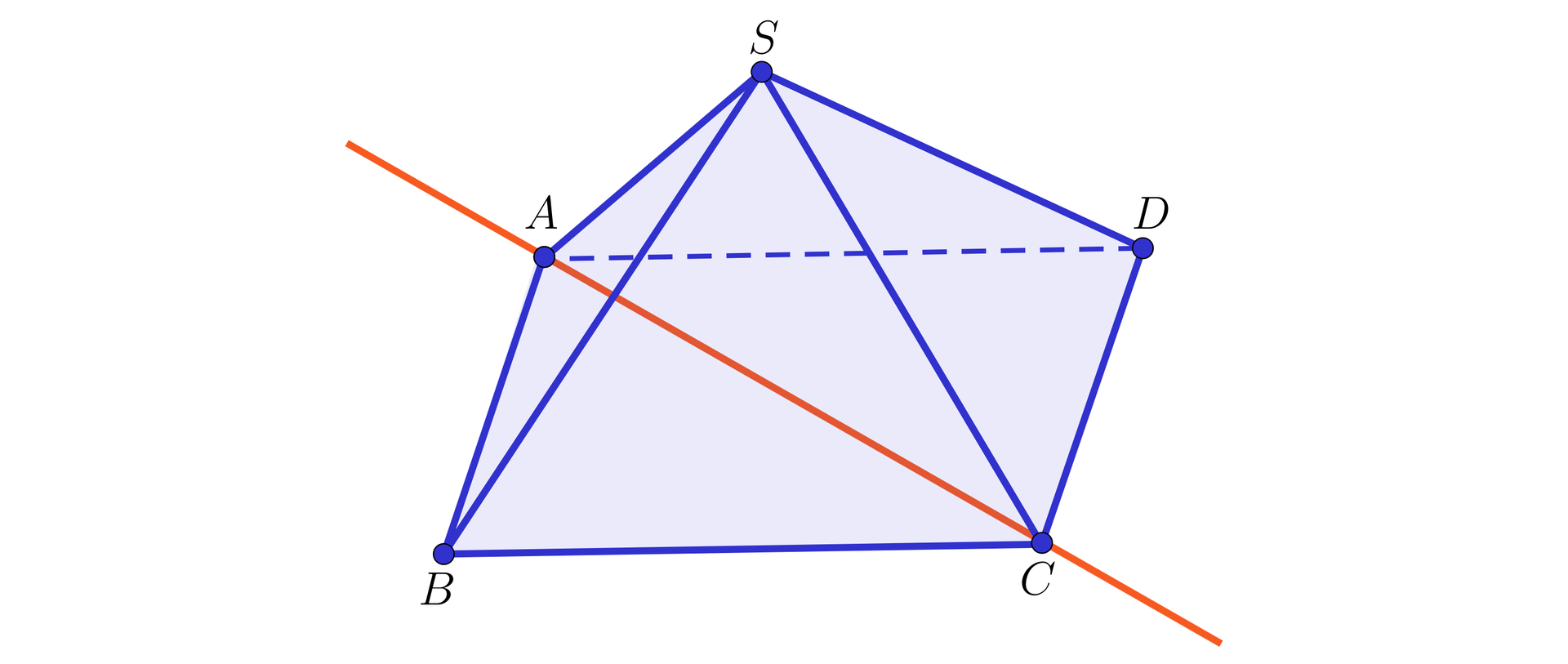
Na rysunku przedstawiony jest ostrosłup czworokątny. Wykażemy, że proste $BS$ i $DS$ są skośne do prostej $AC$, ale nie są skośne do siebie.

RTKsvxNBAa9ey

Ilustracja przedstawia ostrosłup czworokątny A B C D S. Zaznaczono przekątną podstawy bryły A C i przedłużono ją tworząc prostą.

Rozwiązanie

Gdyby proste $BS$ i $AC$ nie były skośne, to leżałyby na jednej płaszczyźnie. Wtedy cztery punkty $B$, $S$, $A$, $C$ leżałyby na jednej płaszczyźnie, w szczególności płaszczyzny $ABS$ i $BCS$ byłyby równe, a tak nie jest. Podobnie pokazujemy, że proste $DS$ i $AC$ są skośne.  

Natomiast proste $BS$ i $DS$ nie są skośne, bo przecinają się w punkcie $S$.

Ponieważ przez punkt $P$ i prostą $l$ można poprowadzić płaszczyznę, to możemy skorzystać z własności planimetrii, która charakteryzuje odległość punktu $P$ od prostej $l$ jako długość odcinka $PP\text{'}$, gdzie $P\text{'}$ jest punktem przecięcia prostej $l$ z prostą prostopadłą do $l$ poprowadzoną przez punkt $P$.

Jeżeli dwie różne proste są równoległe w przestrzeni, to odległość dowolnego punktu jednej prostej od drugiej prostej jest stała niezależnie od wyboru tego punktu.

W przypadku prostych skośnych własność ta nie zachodzi, popatrzmy na przykład:

Przykład 3

Rozważmy ostrosłup prawidłowyostrosłup prawidłowyostrosłup prawidłowy czworokątny, którego podstawa jest kwadratem o boku  długości $1$, a wysokość ma długość $2$. W tym ostrosłupie proste $AC$ i $BS$ są skośne. Pokażemy, że odległość punktu $S$ od prostej $AC$ nie jest równa odległości punktu $B$ od prostej $AC$.

RYmpVvdj6Rx1H

Ilustracja przedstawia ostrosłup prawidłowy czworokątny A B C D S. Zaznaczono wysokość bryły S E. Punkt E znajduje się na środku przekątnej A C. Kolorem pomarańczowym zaznaczono odcinek B S. Powstał trójkąt prostokątny B E S z kątem prostym przy wierzchołku E.

Rozwiązanie

Niech $E$ będzie spodkiem wysokości. Z własności rozważanego ostrosłupa wynika, że punkt $E$ jest punktem przecięcia przekątnych kwadratu. Stąd prosta $SE$ jest prostopadła do prostej $AC$ i $\left|SE\right|=2$ jest odległością punktu $S$ od prostej $AC$. 

Ponieważ przekątne kwadratu przecinają się pod kątem prostym, to prosta $BE$ jest prostopadła do $AC$, a stąd $\left|BE\right|=\frac{\sqrt{2}}{2}$ jest odległością punktu $B$ od prostej $AC$. 

Płaszczyzny zawierające proste skośne

Własność: Płaszczyzny zawierające proste skośne

Załóżmy, że proste $k$, $l$ są skośne. Wtedy istnieją płaszczyzny: ${\pi }_1$ zawierająca $k$ oraz ${\pi }_2$ zawierająca $l$, takie, że ${\pi }_1$ i ${\pi }_2$ są równoległe, czyli nie mają punktów wspólnych.

Dowód

Wybierzmy dowolny punkt $K$ na prostej $k$. Niech $l\text{'}$ będzie prostą równoległą do $l$ i przechodzącą przez $K$. Taka prosta wyznaczona jest jednoznacznie na mocy aksjomatu równoległości. Podobnie, niech $k\text{'}$ będzie prostą równoległą do $k$ przechodzącą przez pewien punkt $L$ leżący na prostej $l$.

Wówczas przez proste $k$ i $l\text{'}$ przechodzi dokładnie jedna płaszczyzna ${\pi }_1$. Podobnie, przez proste $k\text{'}$ i $l$ przechodzi dokładnie jedna płaszczyzna ${\pi }_2$.

Popatrzmy na rysunek.

RKdAmyk0I8N3y

Ilustracja przedstawia dwie do siebie równoległe płaszczyzny. Na pierwszej z nich znajdują się dwie proste zawarte w tej płaszczyźnie przecinające się w punkcie K. Wewnątrz drugiej płaszczyzny także znajdują się dwie proste. Proste te przecinają się w punkcie L.

Pokażemy teraz, że płaszczyzny ${\pi }_1$ i ${\pi }_2$ nie mają punktów wspólnych.

Załóżmy, że $A$ jest punktem wspólnym tych płaszczyzn i poprowadźmy przez ten punkt prostą $l\text{'}\text{'}$ równoległą do $l$ oraz prostą $k\text{'}\text{'}$ równoległą do $k$. Wtedy $l\text{'}\text{'}$ i $l$ leżą w płaszczyźnie ${\pi }_2$. Ponadto, $l\text{'}\text{'}$ jest równoległa do $l\text{'}$, więc $l\text{'}\text{'}$ i $l\text{'}$ leżą w płaszczyźnie ${\pi }_1$. Stąd prosta $l\text{'}\text{'}$ jest krawędzią wspólną płaszczyzn ${\pi }_1$, ${\pi }_2$. Podobne rozumowanie prowadzi do wniosku, że prosta $k\text{'}\text{'}$ jest krawędzią wspólną płaszczyzn ${\pi }_1$, ${\pi }_2$. Ponieważ może być tylko jedna taka krawędź, to $l\text{'}\text{'}=k\text{'}\text{'}$. Stąd wynika, że $l\text{'}\text{'}$ jest równoległa do $k$ a stąd, że $l$ jest równoległa do $k$. To przeczy założeniu, że proste $k$, $l$ są skośne.

Z dowodu powyższej własności wynika, że płaszczyzny równoległepłaszczyzny równoległepłaszczyzny równoległe, na których leżą dane dwie proste skośne są wyznaczone jednoznacznie. Stąd wynika, że odległość między prostymi skośnymi jest odległością między płaszczyznami równoległymi zawierającymi te proste. Ponadto, ${\pi }_1$ jest płaszczyzna zawierającą $k$ i równoległą do prostej $l$, a ${\pi }_2$ jest płaszczyzna zawierającą $l$ i równoległą do prostej $k$.

Przykład 4

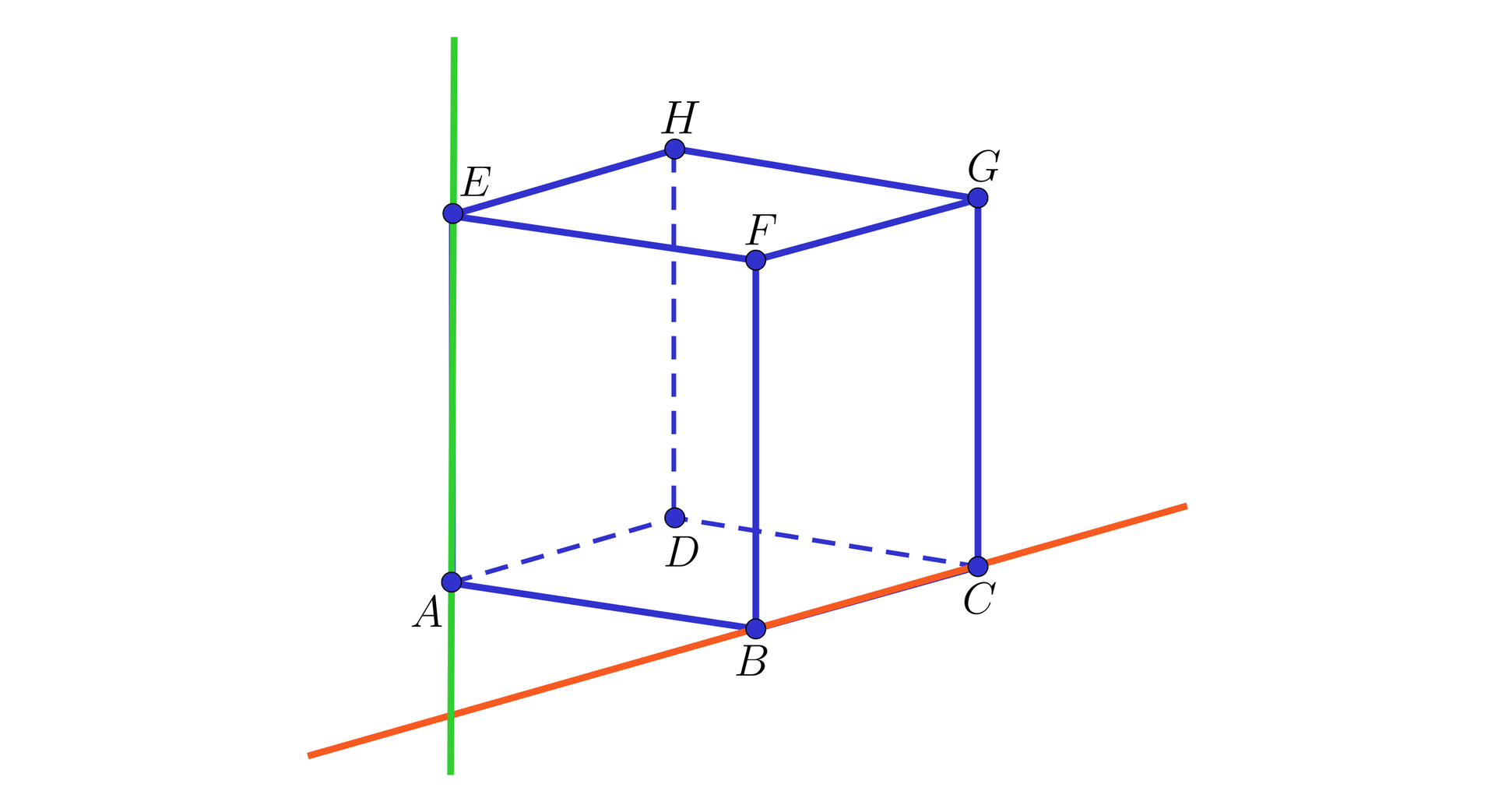
Wyznaczymy płaszczyzny równoległe, w których leżą skośne krawędzie sześcianu $AE$ i $BC$ oraz wyznaczymy odległość między tymi krawędziami.

Rnix6gZ0C1Yzr

Ilustracja przedstawia sześcian A B C D E F G H, gdzie wierzchołek E znajduje się nad A, wierzchołek F nad B, wierzchołek G nad C, wierzchołek H nad D. Przez odcinek B C poprowadzono pomarańczową prostą, natomiast przez odcinek A E poprowadzono zieloną prostą.

Rozwiązanie

Prowadzimy prostą równoległą do $BC$ przez punkt $A$. Z własności sześcianu wynika, że prosta ta zawiera krawędź $AD$. Podobnie prosta równoległa do $AE$ poprowadzona przez punkt $B$ zawiera krawędź $BF$.

R7p0qUMNbFw1c

Ilustracja przedstawia sześcian A B C D E F G H, gdzie wierzchołek E znajduje się nad A, wierzchołek F nad B, wierzchołek G nad C, wierzchołek H nad D. Przez odcinek B C poprowadzono pomarańczową prostą, natomiast przez odcinek A D poprowadzono przerywaną prostą równoległą do prostej B C. Przez odcinek A E poprowadzono zieloną prostą. Przez odcinek B F poprowadzono przerywaną prostą równoległą do prostej A E. Powstały dwie płaszczyzny. Pierwsza płaszczyzna B C G F  zawiera w sobie proste przechodzące przez odcinki B C i B F. Druga płaszczyzna A D H E zawiera w sobie proste przechodzące przez odcinki A E i A D.

Płaszczyzna zawierająca krawędzie $AE$ i $AD$ zawiera ścianę $ADHE$ i jest ona równoległa do płaszczyzny wyznaczonej przez krawędzi $BC$ i $BF$, która zawiera ścianę $BCGF$.

Odległość między prostymi zawierającymi krawędzie $AE$ i $BC$ jest równa odległości między płaszczyznami zawierającymi ściany $ADHE$ i $BCGF$, czyli jest równa długości krawędzi $AB$.

Rysunek przedstawia bryłę nazywaną równoległościanem, zbudowaną na prostych skośnych. Taki równoległościan można zbudować na dowolnych dwóch prostych skośnych i dwóch parach różnych punktów wybranych na tych prostych.

R12FvxR3Wdp0D

Ilustracja przedstawia dwanaście prostych przecinających się w ośmiu szczególnych punktach A, B, I, J, J, L, M, N. Wszystkie proste można podzielić na trzy grupy. Każda prosta należąca do jeden grupy jest do siebie równoległa. Proste z danych trzech grup są pod trzema różnymi kątami.

Konstrukcja równoległościanu wygląda następująco:

1. Na prostej $l$ dane są punkty $A$ i $B$ a na prostej $k$ – punkty $I$ i $J$.

2. Prowadzimy proste $k_A$, $k_B$ równoległe do $k$ przez punkty $A$ i $B$ oraz proste $l_I$, $l_J$ równoległe do $l$ – przez punkty $I$ i $J$.

3. Prowadzimy prostą $AI$ oraz proste $m_B$, $m_I$, $m_J$ równoległe do $AI$ przez punkty $B$, $I$ i $J$.

4. Punkt $M$ jest punktem przecięcia prostych $l_I$, $m_B$, a prosta $k_M$ jest równoległa do $k$ i przechodzi przez punkt $M$. 

5. Punkt $L$ jest punktem przecięcia prostych $k_M$, $l_J$, a prosta $m_L$ jest równoległa do $m$ i przechodzi przez punkt $L$. 

6. Punkt $K$ jest punktem przecięcia prostych $m_L$, $k_B$, a prosta $l_K$ jest równoległa do $l$ i przechodzi przez punkt $K$. 

7. Ostatni punkt $N$ jest punktem przecięcia prostych $l_K$, $k_A$.  

Wówczas płaszczyzna $IJLM$ zawiera prostą $k$ i jest równoległa do płaszczyzny $ABKN$ zawierającej prostą $l$. Prosta $IM$ jest rzutem równoległym prostej $l$ na płaszczyznę $IJLM$ w kierunku prostej $m$, a prosta $AN$ jest rzutem równoległym prostej $k$ na płaszczyznę $ABKN$ w kierunku prostej $m$.

Wszystkie ściany równoległościanu są równoległobokami, a przeciwległe ściany są równoległe i są przystającymi równoległobokami. Szczególnym przypadkiem równoległościanu jest prostopadłościan, czyli równoległościan, którego ściany są prostokątami.

RW5Ly6Reuju6Y

Ilustracja przedstawia dwie proste, prostą k oraz prostą l. Prosta k znajduje się na innej płaszczyźnie. Poprowadzono prostą równoległą do prostej l, na tej samej płaszczyźnie co prosta k. Obie proste przecinają się pod kątem prostym w punkcie K.

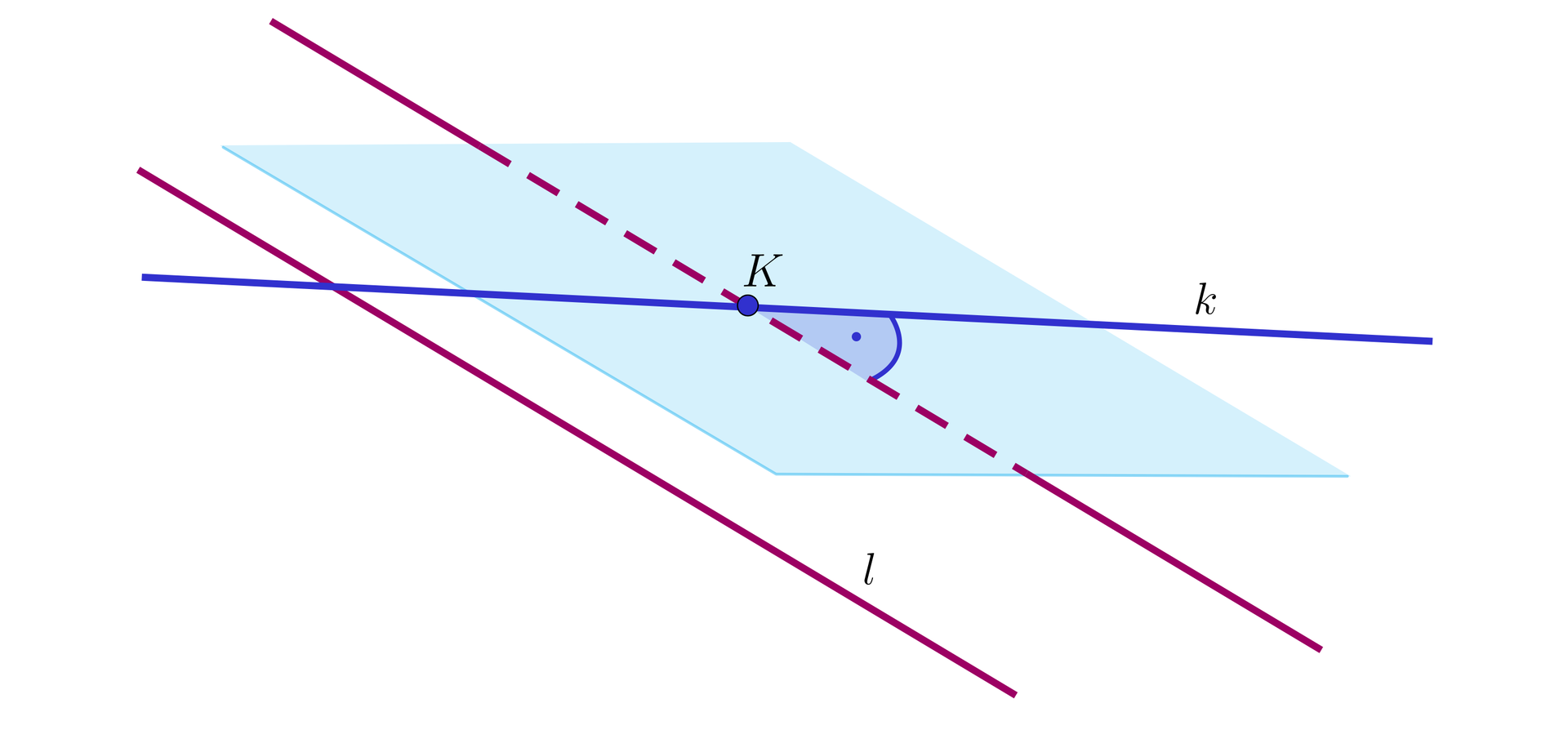
Powyższa konstrukcja równoległościanu pozwala na zdefiniowanie kąta między prostymi skośnymi jako jeden z kątów równoległoboku $IJLM$ (lub $ABKN$). Inaczej mówiąc, kąt między prostymi skośnymi $k$, $l$ jest to kąt między $k$ a rzutem równoległym prostej $l$ na płaszczyznę zawierającą $k$ i równoległą do $l$.

Przykład 5

Rozważmy graniastosłup o podstawie trójkąta prostokątnego równoramiennego. Wyznaczymy kąt między krawędziami skośnymi $AB$ i $GI$.

R1dG7EVNpujNw

Ilustracja przedstawia graniastosłup trójkątny A B C G H I, gdzie wierzchołek H znajduje się nad B, wierzchołek I nad C, wierzchołek G nad A. Przez krawędź A B poprowadzona została pomarańczowa prosta, natomiast przez krawędź I G została poprowadzona zielona prosta.

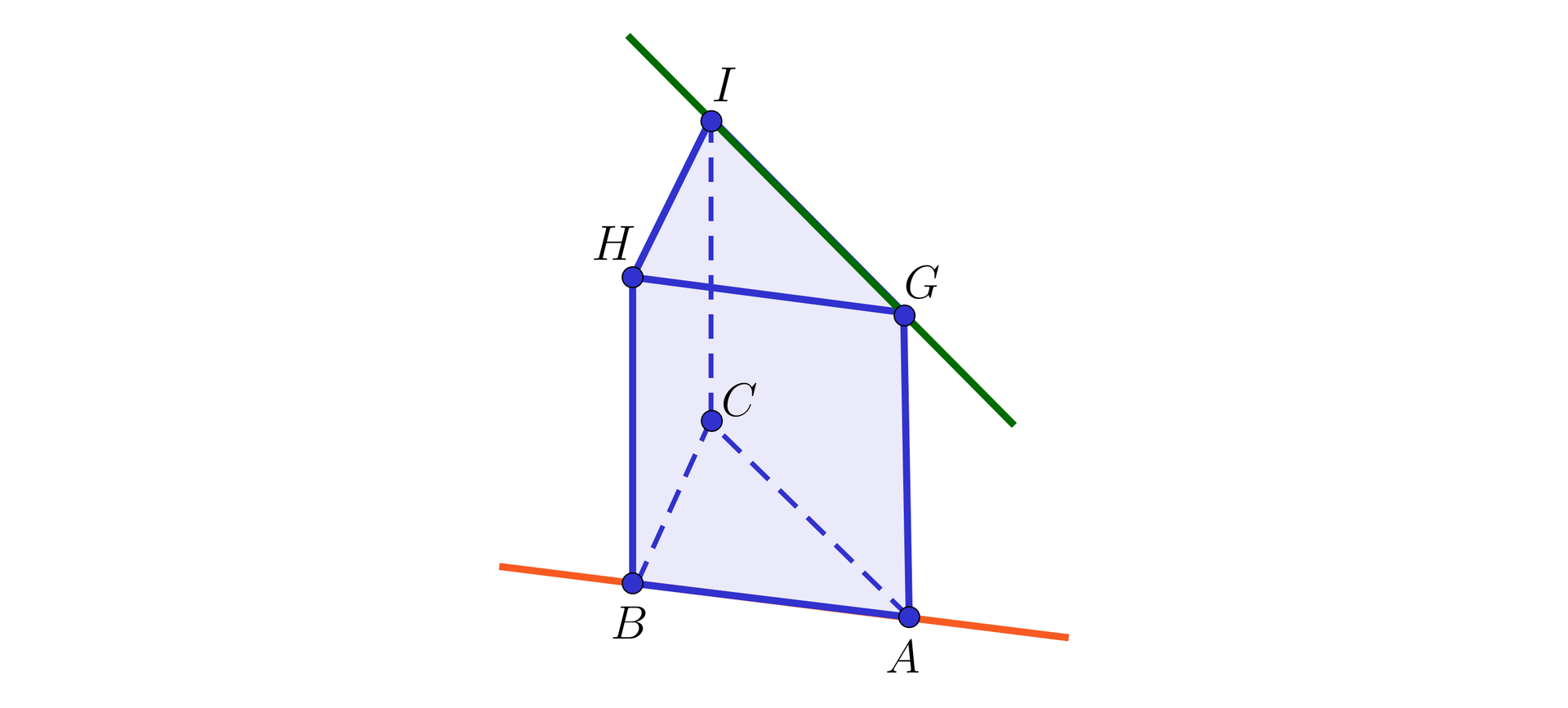
Rozwiązanie

Płaszczyzny zawierające podstawy graniastosłupa są równoległe i zawierają proste skośne $AB$ i $GI$. Krawędź $AC$ jest równoległa do $GI$, więc kąt między krawędziami skośnymi $AB$ i $GI$ jest równy kątowi między krawędziami $AB$ i $AC$. Ponieważ podstawa graniastosłupa jest równoramiennym trójkątem prostokątnym, to kąt $BAC$ ma miarę $45°$.

Słownik