Przeczytaj
Już wiesz
Graniastosłup to wielościanwielościan, którego wszystkie wierzchołki leżą na dwóch płaszczyznach równoległych, zwanych płaszczyznami podstaw, dolnej i górnej, a którego wszystkie krawędzie nie leżące na tych płaszczyznach, zwane krawędziami bocznymi, są równoległe. Graniastosłup nazywamy prostym, jeśli jego krawędzie boczne są prostopadłe do podstaw, w przeciwnym przypadku nazywamy go pochyłym.
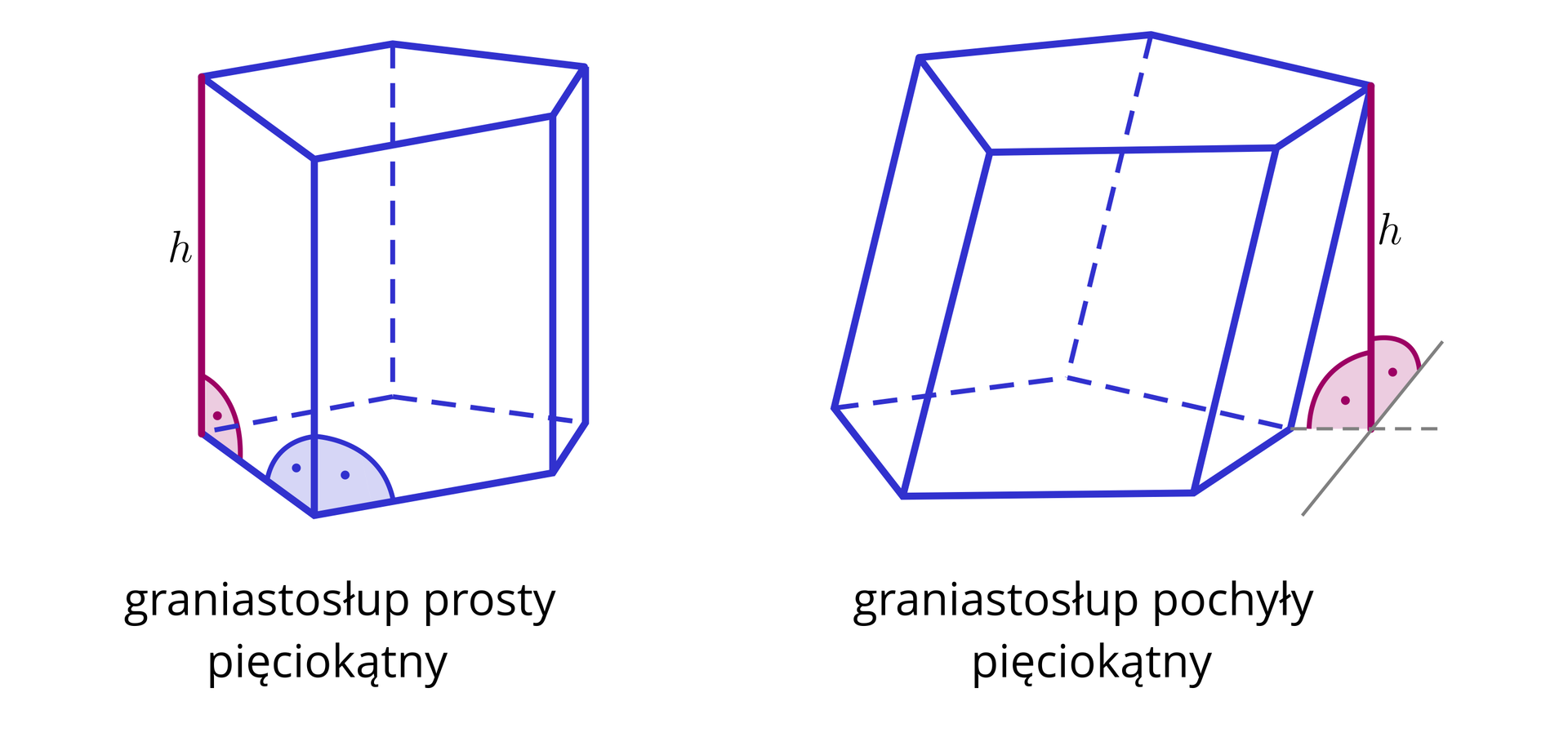
Wprowadzimy teraz pojęcie graniastosłupa prawidłowego i graniastosłupa czworokątnego.
Graniastosłup prawidłowy to graniastosłup prostygraniastosłup prosty, w którym podstawy są przystającymi wielokątami foremnymiwielokątami foremnymi.
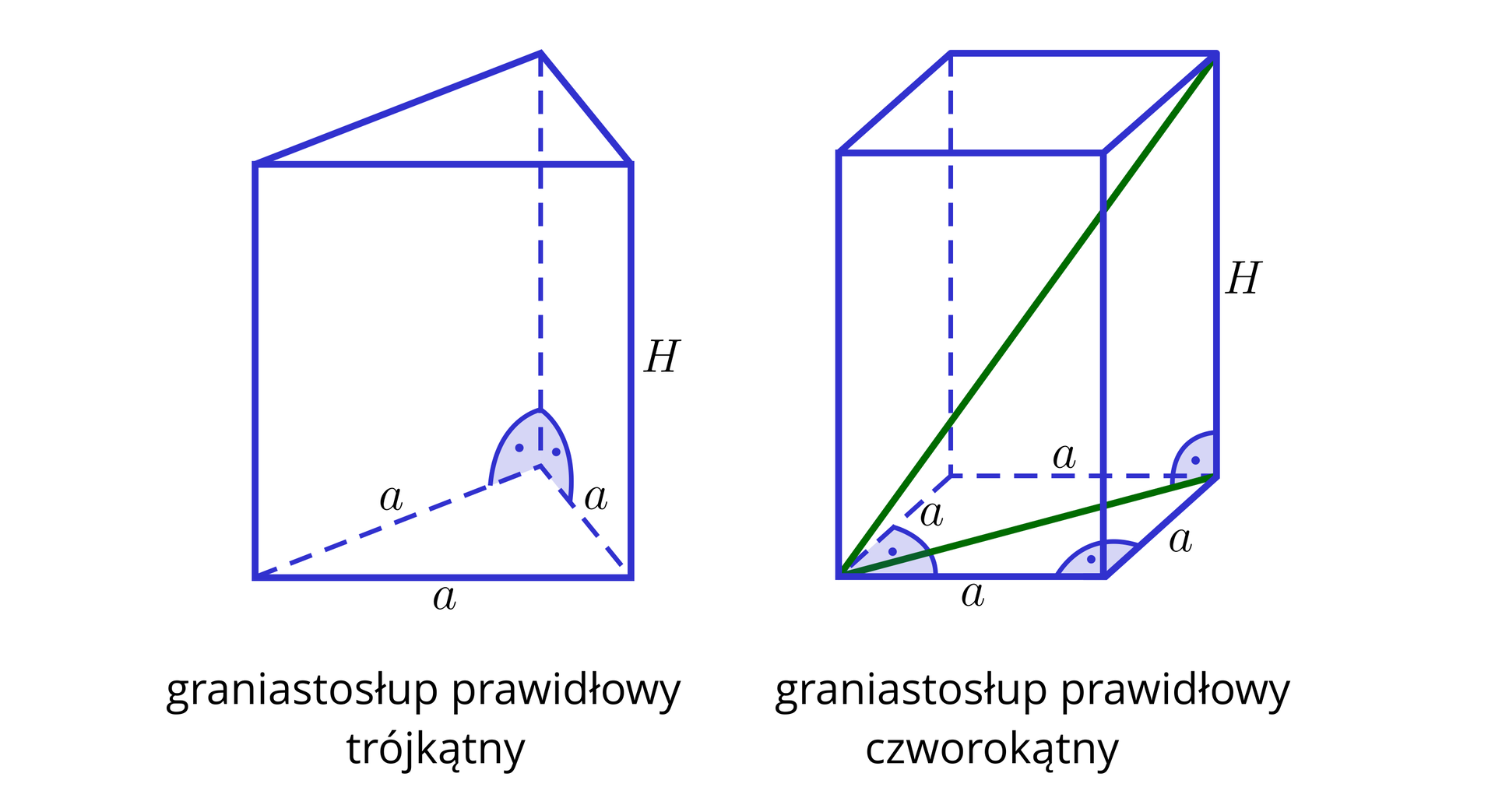
Graniastosłup nazywamy czworokątnymGraniastosłup nazywamy czworokątnym, jeśli jego podstawą jest czworokąt.
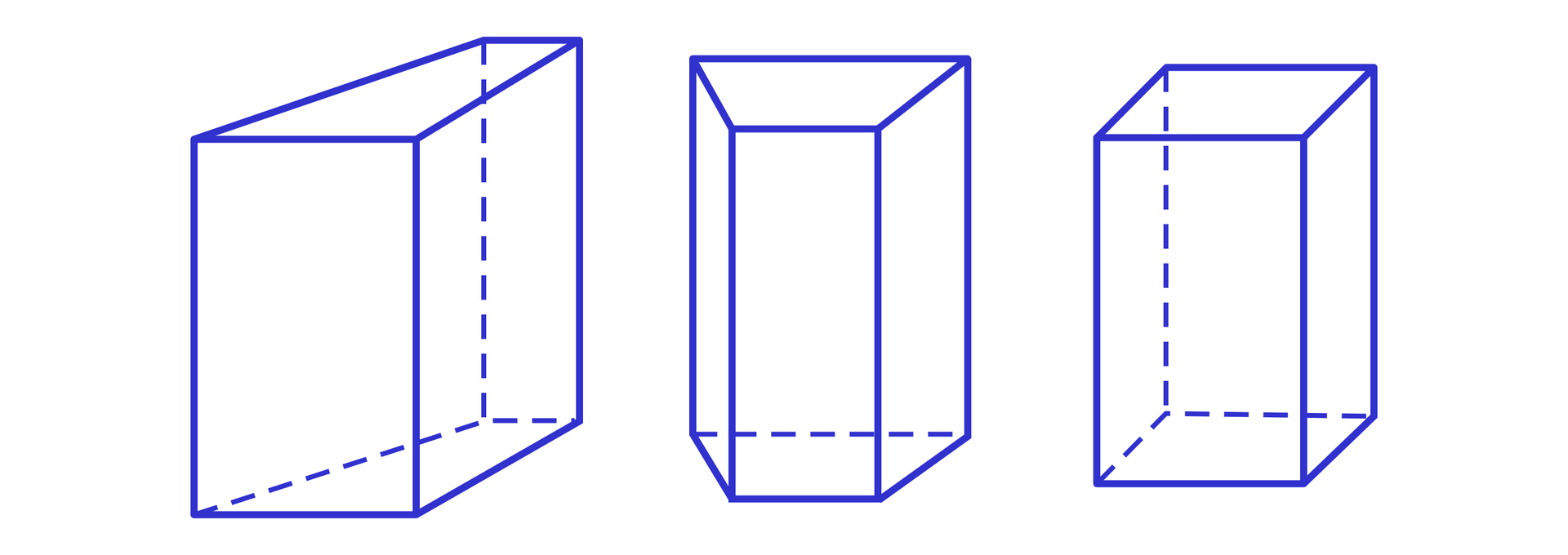
Na podstawie powyższych definicji możemy sformułować definicję graniastosłupa prawidłowego czworokątnego:
Graniastosłupem prawidłowym czworokątnymGraniastosłupem prawidłowym czworokątnym nazywamy graniastosłup prosty, którego podstawy są przystającymi kwadratami.
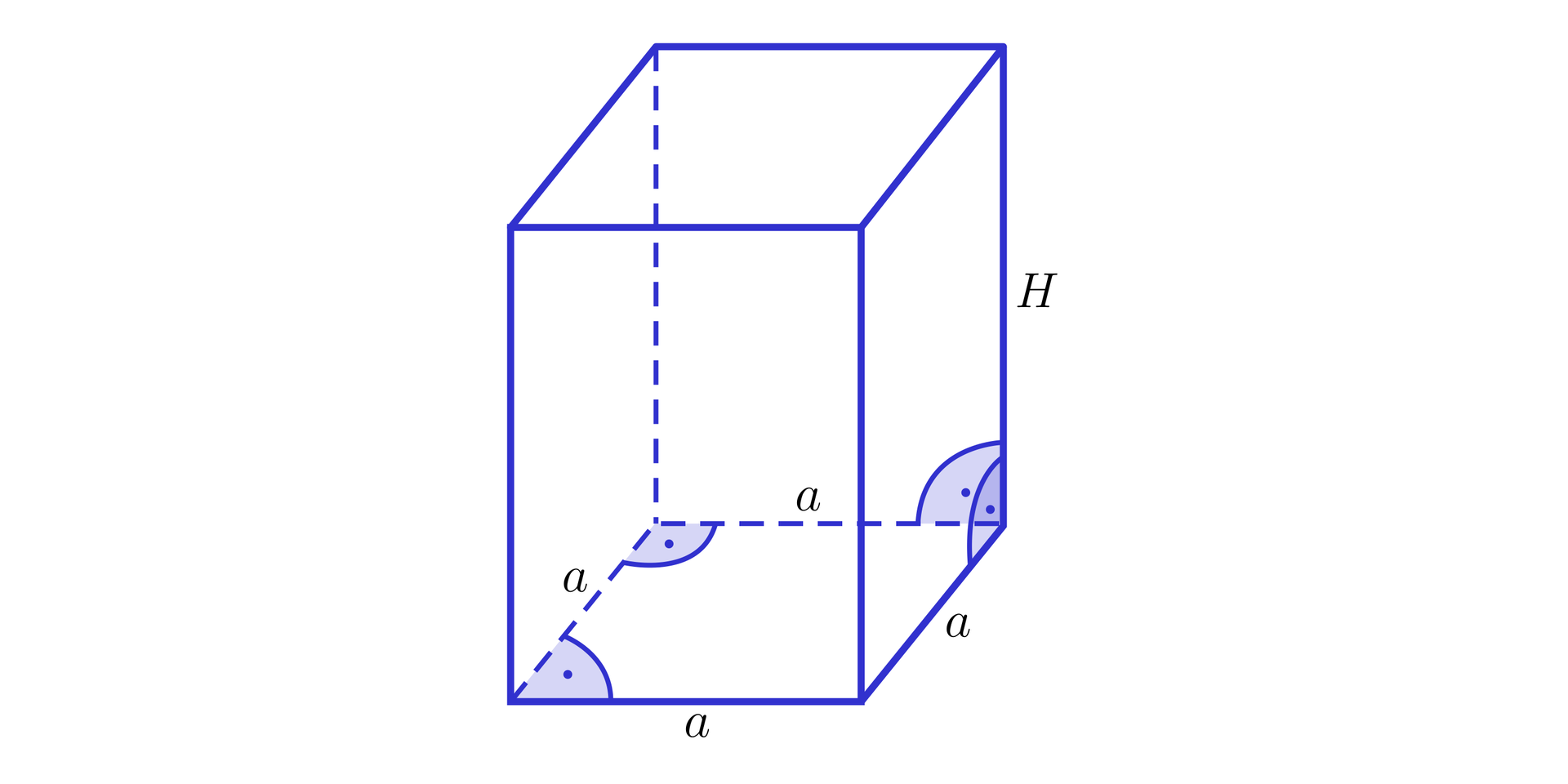
Podstawą graniastosłupa prawidłowegograniastosłupa prawidłowego jest kwadrat, na którym można opisać okrąg o obwodzie . Wysokość graniastosłupa jest trzy razy dłuższa od jego krawędzi podstawy. Obliczymy sumę długości wszystkich krawędzi tego graniastosłupa.
Rozwiązanie
Promień okręgu opisanego na podstawie ma długość: , zatem średnica okręgu, która jest jednocześnie przekatną tego kwadratu ma długość: . Stąd długość boku kwadratu jest równa: .
Wysokość tego graniastosłupa ma zatem długość: .
W graniastosłupie prawidłowym czworokątnym jest krawędzi podstawy i krawędzie boczne, stąd suma długości wszystkich jego krawędzi jest równa:
.
Suma długości krawędzi graniastosłupa prawidłowego czworokątnego, w którym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy, wynosi . Obliczymy pole podstawy tego graniastosłupa.
Rozwiązanie
Oznaczmy długość krawędzi podstawy przez . Krawędź boczna jest dwa razy dłuższa, czyli ma długość . Możemy więc ułożyć równanie:
,
,
.
Obliczymy pole kwadratu będącego podstawą naszego graniastosłupa:
Drut o długości podzielono na trzy różne części. Z każdej części zbudowano graniastosłup prawidłowy czworokątny. Stosunek długości krawędzi podstaw tych graniastosłupów wynosi , a krawędź boczna w każdym graniastosłupie jest o dłuższa od krawędzi podstawy. Wyznaczymy długości krawędzi każdego z tych graniastosłupów.
Rozwiązanie
Oznaczymy długości krawędzi podstaw graniastosłupów odpowiednio przez ; i .
Wtedy długości krawędzi bocznych tych graniastosłupów będą odpowiednio równe: ; i .
Możemy zatem ułożyć równanie:
Zatem najmniejszy graniastosłup ma krawędzie długości i ; krawędzie drugiego graniastosłupa mają długości i ; zaś największy graniastosłup ma krawędzie długości i .
Sprawdzimy, czy z drutu długości można zbudować szkielet bryły będącej graniastosłupem prawidłowym czworokątnym, w którym długości krawędzi podstaw i długości krawiędzi bocznych wyrażone są liczbą całkowitą dodatnią. Rozważymy wszystkie możliwości.
Rozwiązanie
Sprawdzimy najpierw, czy z drutu o podanej długości można zbudować szkielet najprostszej bryły będącej graniastosłupem prawidłowym czworokątnym – szkielet sześcianu.
Niech oznacza długość krawędzi rozważanego sześcianu.
SześcianSześcian ma krawędzi tej samej długości, zatem otrzymujemy równanie , co daje: .
Zatem nie można zbudować szkieletu sześcianu spełniając warunki zadania – wówczas długość krawędzi nie wyraża się liczbą .Rozważymy graniastosłup prawidłowy czworokątny nie będący sześcianem.
Niech oznacza długość krawędzi podstawy a długość krawędzi bocznej rozważanego graniastosłupa.
Mamy krawędzi podstaw o długości oraz krawędzie boczne o długości , więc otrzymujemy równanie , co daje: .
Zatem mamy następujące możliwości długości krawędzi graniastosłupa spełniające warunki zadania: i lub i lub i lub i
Istnieją cztery graniastosłupy prawidłowe czworokątne spełniające warunki zadania.
Podstawę graniastosłupa prawidłowego czworkątnego wpisano w trójkąt równoboczny o boku . Wyznaczymy sumę długości krawędzi tego graniastosłupa, jeśli stosunek długości krawędzi podstawy do długości wysokości wynosi .
Rozwiązanie
Wyznaczymy długość krawędzi podstawy graniastosłupa. Przyjmijmy oznaczenia jak na rysunku:
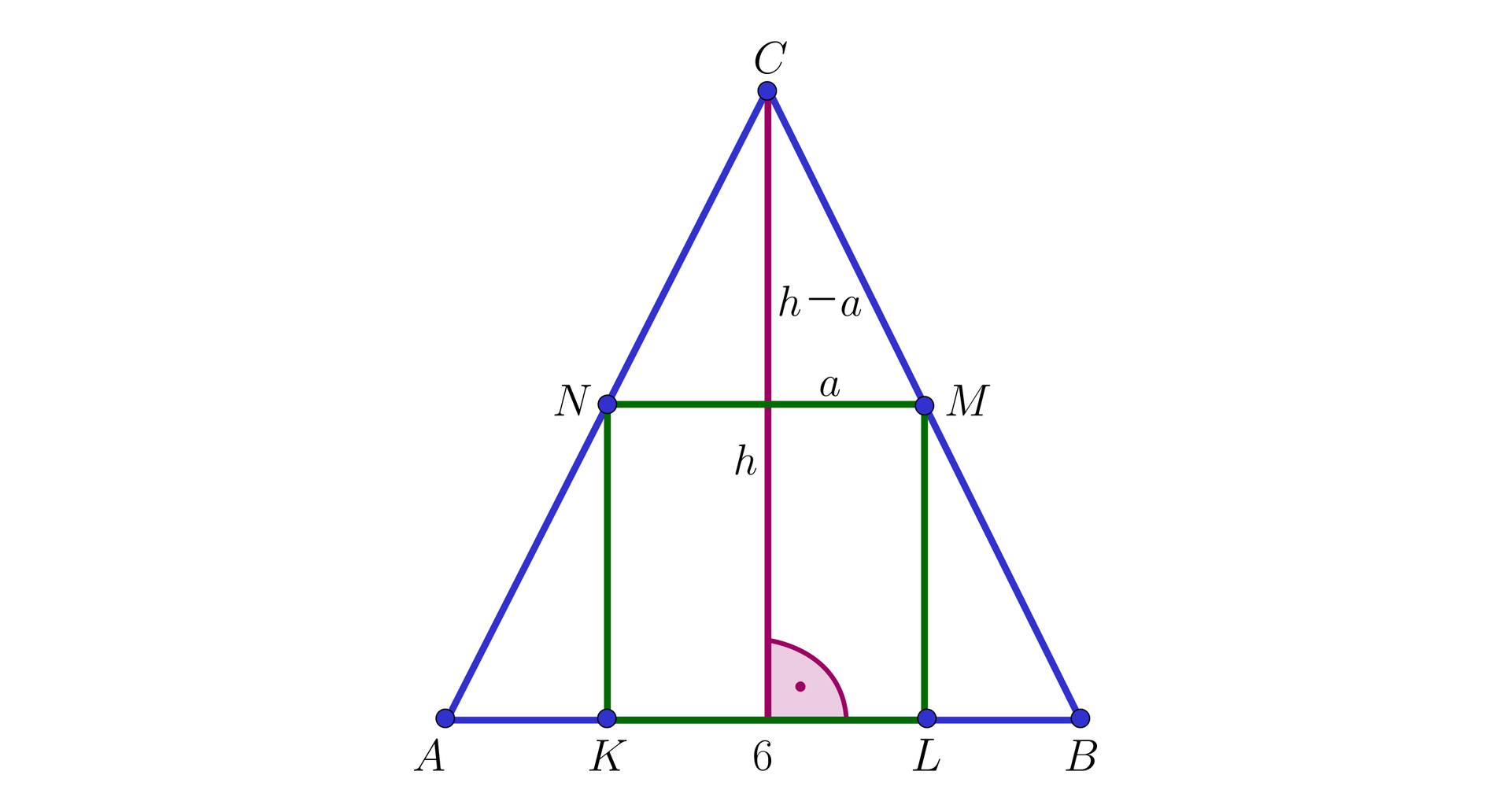
Z podobieństwa trójkątów i mamy:
Wysokość trójkąta ma długość: , zatem:
Zatem wysokość tego graniastosłupa ma długość:
Suma długości krawędzi tego graniastosłupa wynosi:
Przekątne ściany bocznej graniastosłupa prawidłowego czworokątnego o długości przecinają się pod kątem . Wyznaczymy długości krawędzi tego graniastosłupa.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:
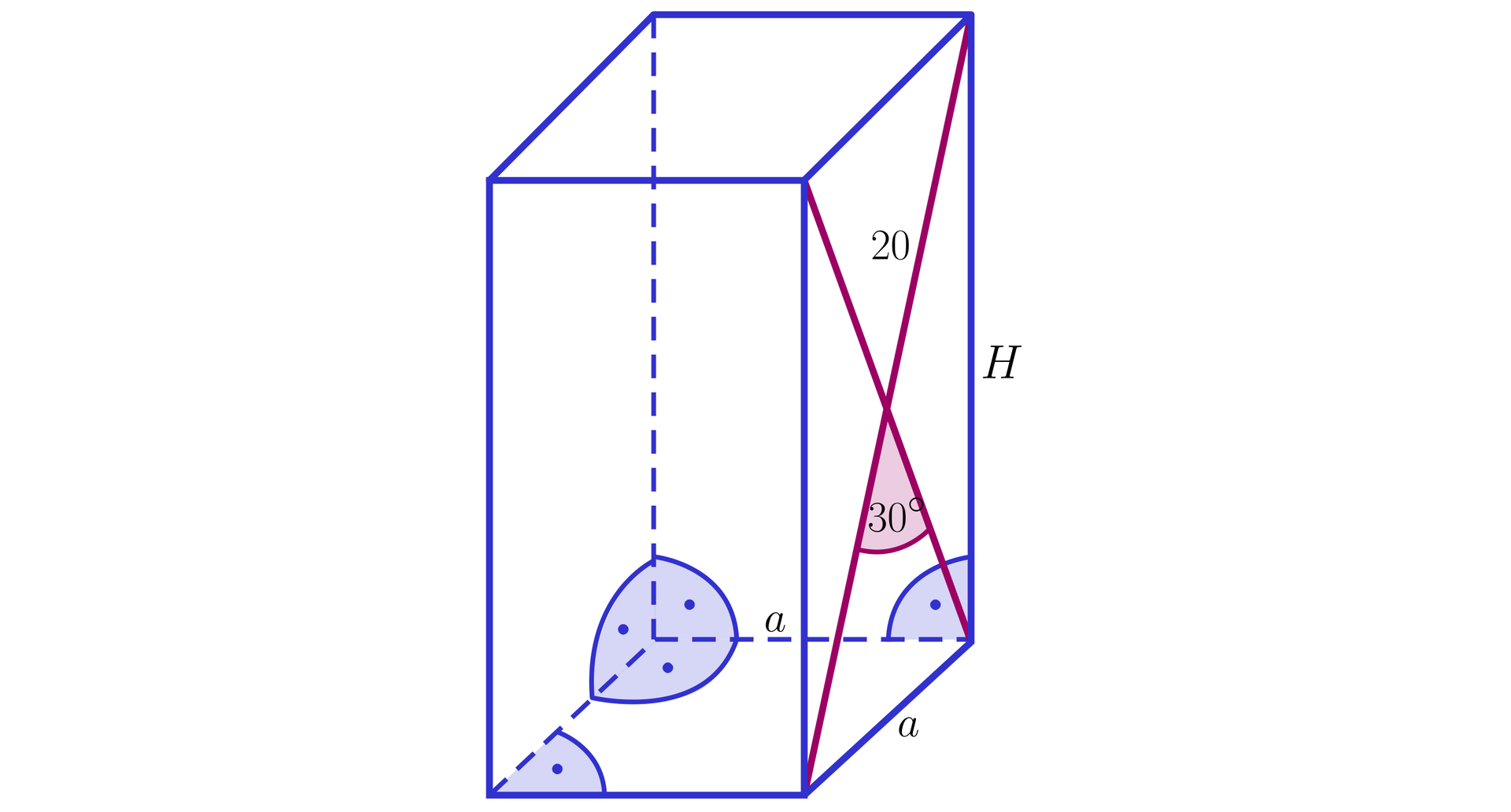
Przekątne prostokąta połowią się. Wyznaczymy długość krawędzi podstawy. Wykorzystamy twierdzenie cosinusów:
Wyznaczymy długość wysokości graniastosłupa:
Słownik
bryła której brzeg jest sumą skończonej liczby wielokątów płaskich.
graniastosłup, którego krawędzie boczne są prostopadłe do podstaw
graniastosłup, którego podstawami są przystające czworokąty
graniastosłup prosty, którego podstawami są przystające wielokąty foremne
graniastosłup prosty, którego podstawy są przystającymi kwadratami
to prostopadłościan, którego wszystkie krawędzie są równe
wielokąt, którego wszystkie boki są równe i wszystkie kąty mają równe miary