Przeczytaj

W tej sekcji znajdziesz przykłady implementacji reprezentacji grafów nieskierowanych bez wag w języku C++. Reprezentacje te zostały przedstawione w e‑materiale teoretycznymPpkZaFlK1e‑materiale teoretycznym, są to macierz sąsiedztwa, lista sąsiedztwa, macierz incydencji.

Grafy nieskierowane

Macierz sąsiedztwa

Dany jest następujący graf spójny nieskierowany bez wag:

R1OA3UoJEctUA

Ilustracja przedstawia pięciokąt wypukły. Jego wierzchołki są oznaczone kolejno cyframi 4, 0, 1, 2, 5. Wierzchołek 4 oraz 1 jest połączony przekątną, tak samo jak wierzchołek 2 i 0. Z wierzchołka 4 oraz 2 wychodzą proste, które spotykają się w punkcie oznaczonym 3, który znajduje się wewnątrz figury. Wszystkie wierzchołki i punkty są oznaczone niebieskimi kółkami. — Graf spójny nieskierowany, który składa się z sześciu wierzchołków i dziewięciu krawędzi.
Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Jego macierz sąsiedztwa wygląda tak:

R12LrCWhJbLTN

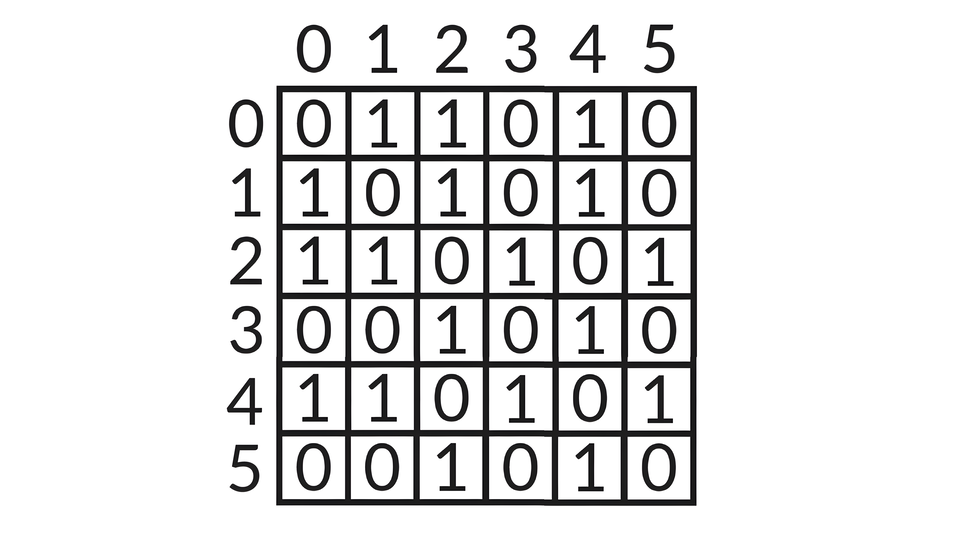
Ilustracja przedstawia tabelkę sześć na sześć kratek. Jej kolumny i rzędy są oznaczone cyframi od 0 do 5. W pierwszym rzędzie wpisano 0, 1, 1, 0, 1, 0, w drugim rzędzie 1, 0, 1, 0, 1, 0, w trzecim rzędzie, 1, 1, 0, 1, 0, 1, w czwartym rzędzie 0, 0, 1, 0, 1, 0, w piątym rzędzie 1, 1, 0, 1, 0, 1, w szóstym rzędzie 0, 0, 1, 0, 1, 0. — Macierz sąsiedztwa zaprezentowanego grafu.
Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Na potrzeby naszej implementacji macierz sąsiedztwa będzie dwuwymiarową tablicą statyczną o n wierszach i n kolumnach (n to liczba wierzchołków grafu), przechowującą elementy typu int.

#include <iostream>
#define n 6
using namespace std;

int macierzSasiedztwa[n][n] = {
	{ 0, 1, 1, 0, 1, 0 },
	{ 1, 0, 1, 0, 1, 0 },
	{ 1, 1, 0, 1, 0, 1 },
	{ 0, 0, 1, 0, 1, 0 },
	{ 1, 1, 0, 1, 0, 1 },
    { 0, 0, 1, 0, 1, 0 }
};

Łączenie wierzchołków nowymi krawędziami zrealizujemy za pomocą funkcji polaczWierzcholki(). Funkcja przyjmuje dwa argumenty i oraz j typu int będące indeksami dwóch wierzchołków, które chcemy połączyć. Aby to zrobić, należy wyrazom macierzSasiedztwa[i][j] i macierzSasiedztwa[j][i] przypisać wartość 1.

void polaczWierzcholki(int i, int j) {
	macierzSasiedztwa[i][j] = 1;
	macierzSasiedztwa[j][i] = 1;
}

Następna funkcja, która wypisze wszystkie wyrazy macierzy sąsiedztwa, ułatwi nam obserwację zmian wartości wyrazów macierzy po każdym uruchomieniu funkcji polaczWierzcholki().

void wypisz(){
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++)
			cout << macierzSasiedztwa[i][j] << " ";
            
		cout << endl;
	}
}

Przykładowe wywołanie wymienionych funkcji możemy znaleźć poniżej. Tablica macierzSasiedztwa[] jest w naszym kodzie zmienną globalnązmienna globalnazmienną globalną zdefiniowaną w programie nad funkcją main().

int main() {
	cout << "Pierwotna postac:" << endl;
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(0, 5);" << endl;
	polaczWierzcholki(0, 5);
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(2, 4);" << endl;
	polaczWierzcholki(2, 4);
	wypisz();

	return 0;
}

Kod programu:

Linia 1. kratka include otwórz nawias ostrokątny iostream zamknij nawias ostrokątny. Linia 2. kratka define n 6. Linia 3. using namespace std średnik. Linia 5. int macierzSasiedztwa otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy n zamknij nawias kwadratowy znak równości otwórz nawias klamrowy. Linia 6. otwórz nawias klamrowy 0 przecinek 1 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 7. otwórz nawias klamrowy 1 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 8. otwórz nawias klamrowy 1 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 9. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 10. otwórz nawias klamrowy 1 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 11. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy. Linia 12. zamknij nawias klamrowy średnik. Linia 14. void polaczWierzcholki otwórz nawias okrągły int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 15. macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy znak równości 1 średnik. Linia 16. macierzSasiedztwa otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy znak równości 1 średnik. Linia 17. zamknij nawias klamrowy. Linia 19. void wypisz otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 20. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 21. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny n średnik j plus plus zamknij nawias okrągły. Linia 22. cout otwórz nawias ostrokątny otwórz nawias ostrokątny macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 24. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 25. zamknij nawias klamrowy. Linia 26. zamknij nawias klamrowy. Linia 28. int main otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 29. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów Pierwotna postac dwukropek cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 30. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 31. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 33. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 34. polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik. Linia 35. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 36. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 38. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 39. polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik. Linia 40. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 42. return 0 średnik. Linia 43. zamknij nawias klamrowy.

#include <iostream>
#define n 6
using namespace std;

int macierzSasiedztwa[n][n] = {
	{ 0, 1, 1, 0, 1, 0 },
	{ 1, 0, 1, 0, 1, 0 },
	{ 1, 1, 0, 1, 0, 1 },
	{ 0, 0, 1, 0, 1, 0 },
	{ 1, 1, 0, 1, 0, 1 },
    { 0, 0, 1, 0, 1, 0 }
};

void polaczWierzcholki(int i, int j) {
	macierzSasiedztwa[i][j] = 1;
	macierzSasiedztwa[j][i] = 1;
}

void wypisz(){
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++)
			cout << macierzSasiedztwa[i][j] << " ";
            
		cout << endl;
	}
}

int main() {
	cout << "Pierwotna postac:" << endl;
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(0, 5);" << endl;
	polaczWierzcholki(0, 5);
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(2, 4);" << endl;
	polaczWierzcholki(2, 4);
	wypisz();

	return 0;
}

Wynik działania programu:

Pierwotna postac:
0 1 1 0 1 0 
1 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 

polaczWierzcholki(0, 5);
0 1 1 0 1 1 
1 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 
1 1 0 1 0 1 
1 0 1 0 1 0 

polaczWierzcholki(2, 4);
0 1 1 0 1 1 
1 0 1 0 1 0 
1 1 0 1 1 1 
0 0 1 0 1 0 
1 1 1 1 0 1 
1 0 1 0 1 0

Przyjrzyjmy się graficznemu przedstawieniu wyniku.

Tak wygląda pierwotna postać macierzy:

RMZb5uA3j5aOO

Ilustracja przedstawia tabelkę sześć na sześć kratek. Jej kolumny i rzędy są ponumerowane od 0 do 5. W pierwszym rzędzie znajdują się następujące cyfry: 0, 1, 1, 0, 1, 0, w drugim rzędzie 1, 0, 1, 0, 1, 0, w trzecim rzędzie 1, 1, 0, 1, 0, 1, w czwartym rzędzie 0, 0, 1, 0, 1, 0 w piątym rzędzie 1, 1, 0, 1, 0, 1, w szóstym rzędzie 0, 0, 1, 0, 1, 0. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Chcemy połączyć wierzchołek 0 oraz 5:

RVITL4mqUTBis

Po połączeniu macierz wygląda następująco:

Rue4hjdslZXQk

Sytuacja wygląda analogicznie w przypadku łączenia innych wierzchołków.

Lista sąsiedztwa

Dany jest następujący graf spójny nieskierowany bez wag:

R1OA3UoJEctUA

Jego lista sąsiedztwa wygląda następująco:

Rri8wpXPrqHIU

Ilustracja przedstawia cyfry znajdujące się w ramkach. Każdy rząd oznaczony jest cyfrą od 0 do 5, która znajduje się w niebieskiej ramce, pozostałe ramki w rzędach są czarne. W pierwszym rzędzie oznaczonym cyfrą 0 w czarnych ramkach znajduje się cyfra 1, strzałka, cyfra 2, strzałka, cyfra 4. W drugim rzędzie oznaczonym cyfrą 1 znajdują się cyfry 0, 2, 4, w trzecim oznaczonym cyfrą 2 cyfry 0, 1, 3, 5, w czwartym rzędzie oznaczonym cyfrą 3 są cyfry 2, 4, w piątym rzędzie oznaczonym cyfrą 4 cyfry 0, 1, 3, 5, a w szóstym rzędzie oznaczonym cyfrą 5 cyfry 2, 4. Wszystkie liczby w rzędach są połączone strzałkami skierowanymi w prawo. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

W języku C++ możemy skorzystać ze standardowej biblioteki szablonów (STLStandard Template LibrarySTL), w której znajduje się implementacja klasy vector. Wektory to kontenery ciągu liczb reprezentujące tablice, których rozmiar może się zmieniać i nie wymagana jest jego deklaracja. Przykładowa implementacja tego kontenera została przedstawiona w filmie w e‑materiale Wprowadzenie do teorii grafów w języku C++P7Y9tbXxGWprowadzenie do teorii grafów w języku C++.

Aby uzyskać dostęp do klasy, importujemy bibliotekę <vector>. Ponieważ vector jest szablonem klasy, należy przy deklaracji listy określić typ przechowywanych elementów. W omawianym przypadku będzie to typ int.

vector<int> wektor;

Klasa oferuje wiele metod, jednak skupimy się tylko na jednej z nich, czyli metodzie push_back(), która dodaje nowy element na końcu wektora. Za jej pomocą będziemy łączyć wierzchołki w grafie, dodając indeks jednego wierzchołka do listy sąsiadów drugiego.

vector<int> wektor;
    
wektor.push_back(4); // wektor: 4
wektor.push_back(5); // wektor: 4, 5
wektor.push_back(7); // wektor: 4, 5, 7

Każdy wierzchołek potrzebuje osobnego wektora sąsiadów, więc całą listę sąsiedztwa przedstawimy za pomocą tablicy statycznej o wyrazach typu vector<int>. Tablicę wektorów możemy zainicjować pewnymi wyrazami w podobny sposób, jak inicjujemy wyrazy tablic statycznych.

#include <iostream>
#include <vector>
#define n 6
using namespace std;

vector<int> listaSasiedztwa[n] = {
	{1, 2, 4},
	{0, 2, 4},
	{0, 1, 3, 5},
	{2, 4},
	{0, 1, 3, 5},
    {2, 4}
};

Jeśli dwa wierzchołki i oraz j chcemy połączyć krawędzią, to do wektora listaSasiedztwa[i] dodajemy wierzchołek j, a do listaSasiedztwa[j] wierzchołek i.

void polaczWierzcholki(int i, int j) {
	listaSasiedztwa[i].push_back(j);
	listaSasiedztwa[j].push_back(i);
}

Aby wypisać zawartość wektora vector, należy użyć pętli zasięgupętla zasięgu (zakresowa)zasięgu, która iteruje po każdym elemencie wektora niezależnie od jego rozmiaru. Taką pętlę definiujemy następująco:

for (int wyraz : lista)
{
	cout << wyraz << " ";
}

Mając na uwadze powyższe własności wektorów, możemy przejść do napisania funkcji wypisz().

void wypisz() {
	for (int i = 0; i < n; i++) {
		cout << i << ": ";
		for (int sasiad : listaSasiedztwa[i])
			cout << sasiad << " "; 
		cout << endl;
	}
}

Wszystkie funkcje opisane w tej sekcji są kompatybilne z pętlą główną programu opisaną dla macierzy sąsiedztwa, dlatego też można je przetestować bez konieczności napisania nowej funkcji main().

Kod programu:

Linia 1. kratka include otwórz nawias ostrokątny iostream zamknij nawias ostrokątny. Linia 2. kratka include otwórz nawias ostrokątny vector zamknij nawias ostrokątny. Linia 3. kratka define n 6. Linia 4. using namespace std średnik. Linia 6. vector otwórz nawias ostrokątny int zamknij nawias ostrokątny listaSasiedztwa otwórz nawias kwadratowy n zamknij nawias kwadratowy znak równości otwórz nawias klamrowy. Linia 7. otwórz nawias klamrowy 1 przecinek 2 przecinek 4 zamknij nawias klamrowy przecinek. Linia 8. otwórz nawias klamrowy 0 przecinek 2 przecinek 4 zamknij nawias klamrowy przecinek. Linia 9. otwórz nawias klamrowy 0 przecinek 1 przecinek 3 przecinek 5 zamknij nawias klamrowy przecinek. Linia 10. otwórz nawias klamrowy 2 przecinek 4 zamknij nawias klamrowy przecinek. Linia 11. otwórz nawias klamrowy 0 przecinek 1 przecinek 3 przecinek 5 zamknij nawias klamrowy przecinek. Linia 12. otwórz nawias klamrowy 2 przecinek 4 zamknij nawias klamrowy. Linia 13. zamknij nawias klamrowy średnik. Linia 15. void polaczWierzcholki otwórz nawias okrągły int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 16. listaSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy kropka push podkreślnik back otwórz nawias okrągły j zamknij nawias okrągły średnik. Linia 17. listaSasiedztwa otwórz nawias kwadratowy j zamknij nawias kwadratowy kropka push podkreślnik back otwórz nawias okrągły i zamknij nawias okrągły średnik. Linia 18. zamknij nawias klamrowy. Linia 20. void wypisz otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 21. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 22. cout otwórz nawias ostrokątny otwórz nawias ostrokątny i otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów dwukropek cudzysłów średnik. Linia 23. for otwórz nawias okrągły int sasiad dwukropek listaSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy zamknij nawias okrągły. Linia 24. cout otwórz nawias ostrokątny otwórz nawias ostrokątny sasiad otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 25. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 26. zamknij nawias klamrowy. Linia 27. zamknij nawias klamrowy. Linia 29. int main otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 30. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów Pierwotna postac dwukropek cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 31. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 32. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 34. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 35. polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik. Linia 36. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 37. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 39. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 40. polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik. Linia 41. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 43. return 0 średnik. Linia 44. zamknij nawias klamrowy.

#include <iostream>
#include <vector>
#define n 6
using namespace std;

vector<int> listaSasiedztwa[n] = {
	{1, 2, 4},
	{0, 2, 4},
	{0, 1, 3, 5},
	{2, 4},
	{0, 1, 3, 5},
    {2, 4}
};

void polaczWierzcholki(int i, int j) {
	listaSasiedztwa[i].push_back(j);
	listaSasiedztwa[j].push_back(i);
}

void wypisz() {
	for (int i = 0; i < n; i++) {
		cout << i << ": "; 
		for (int sasiad : listaSasiedztwa[i])
			cout << sasiad << " ";
		cout << endl;
	}
}

int main() {
	cout << "Pierwotna postac:" << endl;
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(0, 5);" << endl;
	polaczWierzcholki(0, 5);
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(2, 4);" << endl;
	polaczWierzcholki(2, 4);
	wypisz();

	return 0;
}

Wyjście programu:

Pierwotna postac:
0: 1 2 4 
1: 0 2 4 
2: 0 1 3 5 
3: 2 4 
4: 0 1 3 5 
5: 2 4 

polaczWierzcholki(0, 5);
0: 1 2 4 5 
1: 0 2 4 
2: 0 1 3 5 
3: 2 4 
4: 0 1 3 5 
5: 2 4 0 

polaczWierzcholki(2, 4);
0: 1 2 4 5 
1: 0 2 4 
2: 0 1 3 5 4 
3: 2 4 
4: 0 1 3 5 2 
5: 2 4 0

Przyjrzyj się temu, jak w pierwszym przypadku zmieniły się wiersze nr 10 oraz 15.

W drugim przypadku zwróć uwagę na wiersze nr 20 oraz 22.

Macierz incydencji

Dany jest następujący graf spójny nieskierowany bez wag:

R1SLuEuzVC4ye

Jego macierz incydencji wygląda tak:

R1LgaRvPCSjMs

Ilustracja przedstawia tabelę z sześcioma wierszami i 9 kolumnami. Wiersze oznaczone są cyframi od 0 do 5, a kolumny symbolami od e0 do e8. W pierwszym rzędzie znajdują się następujące cyfry: 1, 1, 1, 0, 0, 0, 0, 0, 0, w drugim rzędzie 1, 0, 0, 1, 1, 0, 0, 0, 0, w trzecim rzędzie 0, 1, 0, 1, 0, 1, 1, 0, 0, w czwartym rzędzie 0, 0, 0, 0, 0, 1, 0, 1, 0, w piątym rzędzie 0, 0, 1, 0, 1, 0, 0, 1, 1, w szóstym rzędzie 0, 0, 0, 0, 0, 0, 1, 0, 1. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Analogicznie do macierzy sąsiedztwa inicjujemy macierz incydencji jako dwuwymiarową tablicę statyczną.

#include <iostream>
#define n 6
#define E 20
using namespace std;
int m = 9;

int macierzIncydencji[n][E] = {
	{ 1, 1, 1, 0, 0, 0, 0, 0, 0 },
	{ 1, 0, 0, 1, 1, 0, 0, 0, 0 },
	{ 0, 1, 0, 1, 0, 1, 1, 0, 0 },
	{ 0, 0, 0, 0, 0, 1, 0, 1, 0 },
    { 0, 0, 1, 0, 1, 0, 0, 1, 1 },
	{ 0, 0, 0, 0, 0, 0, 1, 0, 1 },
};

Używamy dyrektywy define E 20, by określić maksymalną liczbę krawędzi w grafie.

Tablica zawiera E kolumn, ale wykorzystywanych jest m kolumn. Wykorzystujemy m kolumn, a pozostałym wyrazom przypisywana jest domyślnie wartość 0.

Zmienna globalna m przechowuje aktualną liczbę krawędzi w grafie i będzie zwiększana o jeden przy każdym udanym połączeniu wierzchołków. Udanym, ponieważ przy każdym wywołaniu funkcja polaczWierzcholki() sprawdzać będzie, czy dodanie nowej krawędzi jest możliwe, a więc czy tablica nie została już zapełniona.

void polaczWierzcholki(int i, int j) {
	if (m >= E) return;
    
	macierzIncydencji[i][m] = 1;
	macierzIncydencji[j][m] = 1;
	m++;
}

Funkcja wypisz() jest bardzo podobna do jej odpowiednika dla macierzy sąsiedztwa, bo zmienia się tylko zasięg wewnętrznej pętli. Warunek j < n przyjmie tym razem postać j < m.

void wypisz() {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++)
			cout << macierzIncydencji[i][j] << " ";    
		cout << endl;
	}
}

Kod programu:

Linia 1. kratka include otwórz nawias ostrokątny iostream zamknij nawias ostrokątny. Linia 2. kratka define n 6. Linia 3. kratka define E 20. Linia 4. using namespace std średnik. Linia 5. int m znak równości 9 średnik. Linia 7. int macierzIncydencji otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy E zamknij nawias kwadratowy znak równości otwórz nawias klamrowy. Linia 8. otwórz nawias klamrowy 1 przecinek 1 przecinek 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 9. otwórz nawias klamrowy 1 przecinek 0 przecinek 0 przecinek 1 przecinek 1 przecinek 0 przecinek 0 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 10. otwórz nawias klamrowy 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 1 przecinek 0 przecinek 0 zamknij nawias klamrowy przecinek. Linia 11. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 zamknij nawias klamrowy przecinek. Linia 12. otwórz nawias klamrowy 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 przecinek 0 przecinek 0 przecinek 1 przecinek 1 zamknij nawias klamrowy przecinek. Linia 13. otwórz nawias klamrowy 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 0 przecinek 1 przecinek 0 przecinek 1 zamknij nawias klamrowy przecinek. Linia 14. zamknij nawias klamrowy średnik. Linia 16. void polaczWierzcholki otwórz nawias okrągły int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 17. if otwórz nawias okrągły m zamknij nawias ostrokątny znak równości E zamknij nawias okrągły return średnik. Linia 19. macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości 1 średnik. Linia 20. macierzIncydencji otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości 1 średnik. Linia 21. m plus plus średnik. Linia 22. zamknij nawias klamrowy. Linia 24. void wypisz otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 25. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 26. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny m średnik j plus plus zamknij nawias okrągły. Linia 27. cout otwórz nawias ostrokątny otwórz nawias ostrokątny macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów cudzysłów średnik. Linia 28. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 29. zamknij nawias klamrowy. Linia 30. zamknij nawias klamrowy. Linia 32. int main otwórz nawias okrągły zamknij nawias okrągły otwórz nawias klamrowy. Linia 33. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów Pierwotna postac dwukropek cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 34. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 35. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 37. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 38. polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły średnik. Linia 39. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 40. cout otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 42. cout otwórz nawias ostrokątny otwórz nawias ostrokątny cudzysłów polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik cudzysłów otwórz nawias ostrokątny otwórz nawias ostrokątny endl średnik. Linia 43. polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły średnik. Linia 44. wypisz otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 46. return 0 średnik. Linia 47. zamknij nawias klamrowy.

#include <iostream>
#define n 6
#define E 20
using namespace std;
int m = 9;

int macierzIncydencji[n][E] = {
	{ 1, 1, 1, 0, 0, 0, 0, 0, 0 },
	{ 1, 0, 0, 1, 1, 0, 0, 0, 0 },
	{ 0, 1, 0, 1, 0, 1, 1, 0, 0 },
	{ 0, 0, 0, 0, 0, 1, 0, 1, 0 },
    { 0, 0, 1, 0, 1, 0, 0, 1, 1 },
	{ 0, 0, 0, 0, 0, 0, 1, 0, 1 },
};

void polaczWierzcholki(int i, int j) {
	if (m >= E) return;
    
	macierzIncydencji[i][m] = 1;
	macierzIncydencji[j][m] = 1;
	m++;
}

void wypisz() {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++)
			cout << macierzIncydencji[i][j] << " ";    
		cout << endl;
	}
}

int main() {
	cout << "Pierwotna postac:" << endl;
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(0, 5);" << endl;
	polaczWierzcholki(0, 5);
	wypisz();
	cout << endl;

	cout << "polaczWierzcholki(2, 4);" << endl;
	polaczWierzcholki(2, 4);
	wypisz();

	return 0;
}

Wynik działania programu:

Pierwotna postac:
1 1 1 0 0 0 0 0 0 
1 0 0 1 1 0 0 0 0 
0 1 0 1 0 1 1 0 0 
0 0 0 0 0 1 0 1 0 
0 0 1 0 1 0 0 1 1 
0 0 0 0 0 0 1 0 1 

polaczWierzcholki(0, 5);
1 1 1 0 0 0 0 0 0 1 
1 0 0 1 1 0 0 0 0 0 
0 1 0 1 0 1 1 0 0 0 
0 0 0 0 0 1 0 1 0 0 
0 0 1 0 1 0 0 1 1 0 
0 0 0 0 0 0 1 0 1 1 

polaczWierzcholki(2, 4);
1 1 1 0 0 0 0 0 0 1 0 
1 0 0 1 1 0 0 0 0 0 0 
0 1 0 1 0 1 1 0 0 0 1 
0 0 0 0 0 1 0 1 0 0 0 
0 0 1 0 1 0 0 1 1 0 1 
0 0 0 0 0 0 1 0 1 1 0

Zwróć uwagę, że po prawej stronie pojawiły się nowe kolumny – odpowiadają nowo powstałym krawędziom grafu.

Słownik

graf

struktura składająca się z niepustego zbioru wierzchołków oraz rodziny krawędzi; dla grafu G zbiór wierzchołków oznaczamy jako V(G) (ang. verticies – wierzchołki), a zbiór krawędzi – E(G) (ang. edges – krawędzie); liczbę elementów zbioru V(G) oznaczamy literą n; liczbę elementów zbioru E(G) – m (opracowano na podstawie: R. Wilson, Wprowadzenie do teorii grafów, PWN, Warszawa 2007)

graf spójny

graf, w którym każda para wierzchołków połączona jest drogą

graf ważony

graf którego krawędzie mają przypisane wagi

incydencja

relacja między dwoma wierzchołkami a łączącą je krawędzią; mówimy, że dwa sąsiednie wierzchołki połączone pewną krawędzią są incydentne z tą krawędzią

izomorfizm

własność grafów mówiąca o tym, że liczba krawędzi łączących dane dwa wierzchołki jednego grafu jest równa liczbie krawędzi łączących odpowiadające im wierzchołki drugiego grafu (opracowano na podstawie: R. Wilson, Wprowadzenie do teorii grafów, PWN, Warszawa 2007)

krawędź

nieuporządkowana para (niekoniecznie różnych) elementów zbioru wierzchołków (opracowano na podstawie: R. Wilson, Wprowadzenie do teorii grafów, PWN, Warszawa 2007)

lista sąsiedztwa

zestaw $| V |$ uporządkowanych list, gdzie lista o indeksie $i$ jest listą wszystkich sąsiadów wierzchołka $i$

macierz

dwuwymiarowa tablica elementów (zwykle liczbowych), licząca $n$ wierszy i $m$ kolumn

macierz incydencji

macierz zerojedynkowa $M$ rozmiaru $| V | \times | E |$ , dla której każda krawędź grafu musi mieć unikatowy indeks; wyraz $m_{i,e}$ jest równy $1$ , o ile krawędź o indeksie $e$ jest incydentna do wierzchołka $i$

macierz sąsiedztwa

macierz zerojedynkowa $A$ rozmiaru $| V | \times | V |$ , w której wyraz $a_{i,j}$ jest równy $1$ , jeśli wierzchołki $i$ oraz $j$ są sąsiednie, a $0$ w przeciwnym przypadku; macierz sąsiedztwa jest symetryczna dla grafów nieskierowanych

najkrótsza ścieżka

ścieżka w grafie o najmniejszej sumie wag wszystkich krawędzi należących do ścieżki

pętla zasięgu (zakresowa)

pętla for pozwalająca iterować przez zdefiniowany zakres

Standard Template Library

biblioteka dla języka C++, zawierająca cztery komponenty zwane algorytmami, kontenerami, funkcjami i iteratorami; STL posiada zestaw zdefiniowanych szablonów klas, między innymi vector, list, set, map, queue, stack i wiele więcej

stopień wierzchołka

liczba krawędzi incydentnych z danym wierzchołkiem (opracowano na podstawie: R. Wilson, Wprowadzenie do teorii grafów, PWN, Warszawa 2007)

waga krawędzi

wartość przypisana krawędzi grafu

wierzchołek

pojedynczy punkt w przestrzeni, który wraz ze zbiorem krawędzi (będących parami wierzchołków) tworzy graf; krawędzie wychodzą z wierzchołka i łączą się w nim

zmienna globalna

zmienna istniejąca przez cały czas życia programu i widziana z wielu miejsc w programie

Wprowadzenie

Prezentacja multimedialna

Grafy nieskierowane

Macierz sąsiedztwa

Lista sąsiedztwa

Macierz incydencji

Słownik