Przeczytaj
Zapisz program wykorzystujący rekurencję, który wypisze kolejne kroki, jakie trzeba wykonać, aby przenieść wieżę składającą się z n krążków o różnej średnicy ze słupka A na słupek C. Swój program przetestuj dla 5 krążków.
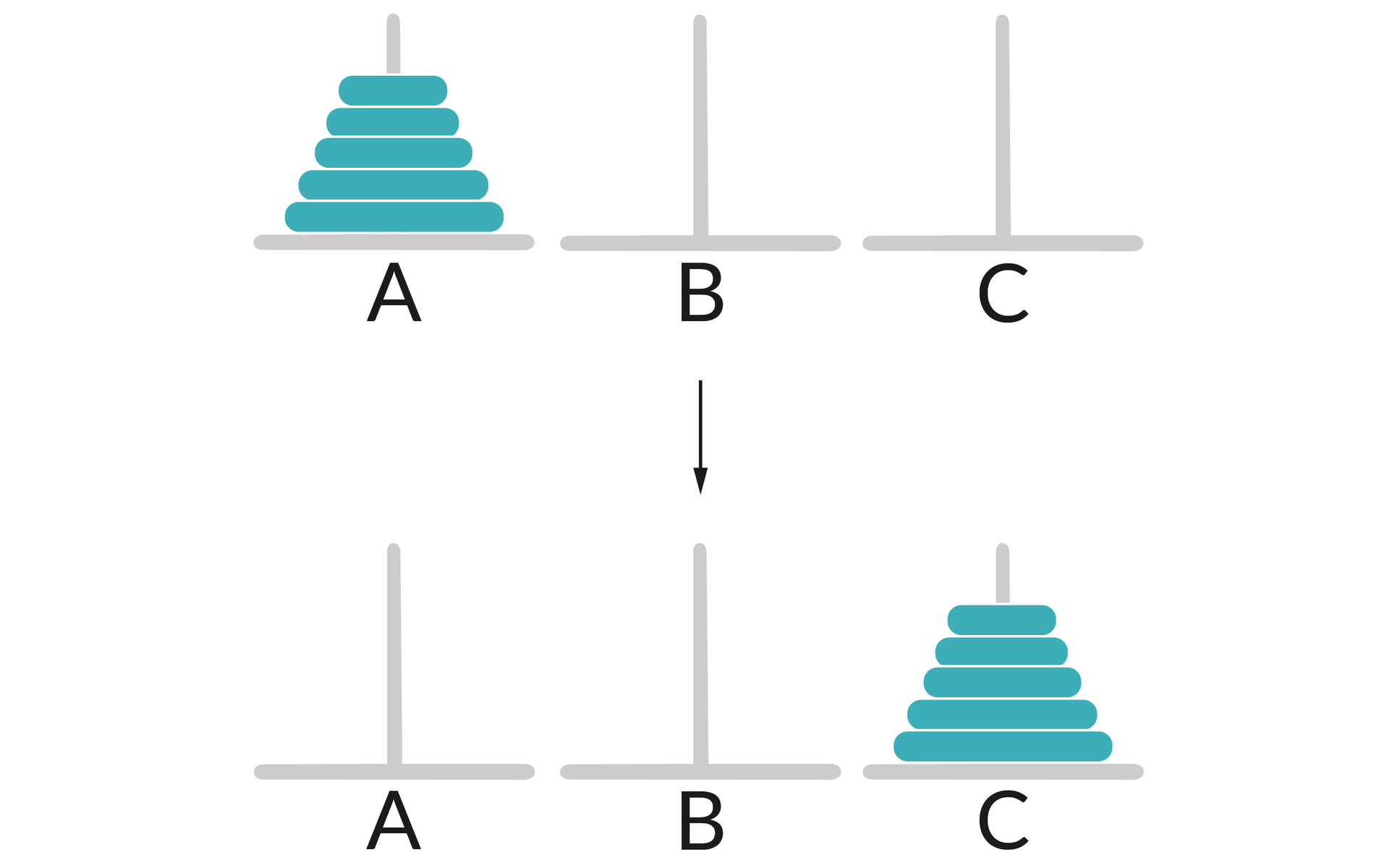
Zasady gry:
Gra składa się z trzech słupków i zestawu krążków o różnych średnicach.
Na jednym słupku umieszczona jest wybudowana wieża.
Celem gry jest odbudowanie wieży na trzecim słupku.
Nie wolno położyć krążka o większej średnicy na krążku o mniejszej średnicy.
Na raz można przenosić tylko jeden krążek (znajdujący się na szczycie wieży).
Do przenoszenia można wykorzystać dodatkowy słupek.
Specyfikacja problemu:
Dane:
n– liczba krążków w grze, liczba naturalnaA, B, C– symboliczne nazwy słupków, znaki
Wynik:
Program, na wyjściu standardowym, wypisuje w kolejnych linijkach kroki, które prowadzą do rozwiązania zagadki Wież Hanoi.
Porównaj swoje rozwiązanie z przedstawionym w filmie.

Film dostępny pod adresem /preview/resource/R1bVBYyDekoQo
Film nawiązujący do treści materiału zagadki wież Hanoi.
Kod programu zaprezentowanego w filmie:
Przedstawienie problemu
Wiesz już, że zagadka Wież Hanoizagadka Wież Hanoi polega na przeniesieniu krążków o różnych rozmiarach z jednego słupka na drugi. Warunkiem poprawnego rozwiązania zadania jest pojedyncze przenoszenie każdego krążka, a także brak możliwości położenia większego krążka na mniejszym. Do dyspozycji mamy jednak pomocniczy słupek, na który możemy tymczasowo odkładać krążki.
Mamy zatem trzy słupki: A, B, C oraz n krążków. Początkowo wszystkie krążki położone są na słupku A, w kolejności od największego do najmniejszego. Docelowo wszystkie krążki mają znaleźć się na słupku C w tej samej kolejności, w jakiej znajdowały się na słupku A. Pomocniczym słupkiem jest słupek B. Celem naszego zadania jest przedstawienie ciągu ruchów, opisującego rozwiązanie zagadki Wież Hanoi.
Implementacja rozwiązania w języku Java
Problem Wież Hanoi można rozwiązać w sposób iteracyjny, czyli za pomocą pętli. Jest on jednak bardzo dobrym przykładem sytuacji, gdzie możemy zastosować rozwiązanie rekurencyjnerekurencyjne, czyli takie, w którym używamy metody „dziel i zwyciężaj”. Operacje niezbędne do umieszczenia coraz mniejszych krążków na słupku docelowym (C) są takie same jak w przypadku pierwszego, największego krążka – z tym zastrzeżeniem, że zmienia się słupek pomocniczy. Najpierw (czyli po przeniesieniu największego krążka na słupek C) będzie nim A. Później rolę słupka pomocniczego będą na przemian odgrywać słupki B i A. Zauważmy, że słupek docelowy się nie zmienia.
Przypadkiem rekurencyjnymPrzypadkiem rekurencyjnym będzie sytuacja, w której na słupku A pozostał co najmniej jeden krążek. Instrukcje składające się na funkcję rekurencyjną hanoi() będą wówczas wykonywane. Przypadkiem bazowymPrzypadkiem bazowym będzie sytuacja, w której na słupku A nie ma już żadnego krążka. Aktualne wywołanie funkcji hanoi() przestanie być wtedy wykonywane.
Należy pamiętać, aby w funkcji rekurencyjnej zawsze opisać przypadek bazowy, który określi, kiedy funkcja powinna się zatrzymać. Bez zdefiniowanego przypadku bazowego funkcja teoretycznie będzie wywoływać samą siebie w nieskończoność. W praktyce nastąpi moment, w którym zostaną wyczerpane zasoby przydzielone programowi, co zakończy się jego awarią. Taką sytuację nazywamy przepełnieniem stosu.
Przepełnienie stosu (ang. Stack overflow) polega na wyczerpaniu miejsca zarezerwowanego na stos. Spowodowane jest ono właśnie nadmierną bądź nieskończoną rekurencją. Kiedy używamy języka Java, mamy domyślnie do dyspozycji stos o rozmiarze 512 KB, a przekroczenie tej wartości sygnalizowane jest zgłoszeniem błędu StackOverflowError.
Oto implementacja algorytmu w języku Java dla 5 krążków:
Po uruchomieniu programu otrzymamy następujący wynik:
Jest to gotowe rozwiązanie problemu Wież Hanoi dla 5 krążków.
Złożoność czasowa i pamięciowa
Jak możemy zauważyć, do rozwiązania problemu Wież Hanoi dla 5 krążków potrzebne było 31 ruchów. Gdybyśmy uruchomili ten program dla 10 krążków, potrzebne byłyby aż 1023 ruchy.
Aby rozwiązać problem Wież Hanoi dla krążków, należy przenieść jeden krążek oraz rozwiązać dwukrotnie ten problem dla . Oznacza to, że liczba wykonanych przeniesień jest równa . Algorytm ma zatem złożoność wykładniczą .
Złożoność pamięciowa tego algorytmu jest liniowa, czyli równa . Wynika to z faktu, że funkcje wywołane w jednej funkcji rekurencyjnej nie wywołają się jednocześnie — drugie wywołanie pojedynczej funkcji będzie miało miejsce dopiero po zakończeniu całości pierwszego wywołania. Zatem pamięć ta może być użyta ponownie. W tym samym momencie aktywnych będzie maksymalnie funkcji.
Słownik
funkcja, która wywołuje samą siebie, aż do momentu osiągnięcia stanu początkowego
myślenie polegające na tym, że wartość pewnej wielkości obliczana jest poprzez odwołanie się do tej samej wielkości określonej dla mniejszych wartości parametrów
warunek w funkcji rekurencyjnej, po którego spełnieniu funkcja nie wywołuje samej siebie po raz kolejny
warunek w funkcji rekurencyjnej, po którego spełnieniu funkcja ponownie wywołuje siebie samą
problem polegający na przeniesieniu wieży z krążków o różnej średnicy z jednego słupka na drugi, przy czym można przenosić tylko po jednym krążku z wierzchu stosu; nie jest dozwolone położenie większego krążka na mniejszym
złożoność, która jest określona za pomocą funkcji wykładniczej, rośnie wykładniczo w zależności od rozmiaru danych wejściowych i można ją zapisać jako