Zadanie 1. Wieże Hanoi

W problemie Wież Hanoi mamy trzy pręty oznaczone A, B i C oraz $n$ okrągłych krążków o średnicach odpowiednio 1, 2, …, $n$. Na początku wszystkie krążki nałożone są na pręt A, w kolejności od największego do najmniejszego (największy na dole, najmniejszy na górze). Układ ten (dla $n = 3$) został przedstawiony na poniższym rysunku.

RCUt0MwYeVqhf

Ilustracja przedstawia trzy pręty oznaczone jako A, B, C. Na pierwszym pręcie są trzy krążki - od dołu do góry od największego do najmniejszego, są ponumerowane 3, 2, 1.

Zgodnie z regułami problemu krążki można przekładać między prętami. W jednym ruchu możliwe jest przełożenie krążka znajdującego się na szczycie jednego z prętów na szczyt innego pręta, pod warunkiem że nie kładziemy przekładanego krążka na krążek mniejszy od niego. Na przykład na poniższym rysunku krążek 2 możemy przełożyć z pręta A na pręt C, natomiast niemożliwe jest przełożenie go na pręt B.

RS5PtZscZla1J

Ilustracja przedstawia trzy pręty oznaczone jako A, B, C. Na pierwszym pręcie są dwa krążki - od dołu do góry od większego do mniejszego, są ponumerowane 3, 2. Na pręcie oznaczonym literą B jest jeden krążek z numerem 1.

Zadanie polega na przełożeniu wszystkich krążków z pręta A na pręt B, przy czym można korzystać z pomocniczego pręta C. Na poniższym rysunku przedstawiono efekt końcowy.

RjTmxxWKV3dod

Ilustracja przedstawia trzy pręty oznaczone jako A, B, C. Na środkowym pręcie B są trzy krążki - od dołu do góry od największego do najmniejszego, są ponumerowane 3, 2, 1.

Problem wież z Hanoi można rozwiązać za pomocą algorytmu rekurencyjnego. W algorytmie pręty: startowy, docelowy i pomocniczy, podane są jako parametry wejściowe, odpowiednio $x$, $y$ i $z$. Algorytm polega na tym, że najpierw przenosimy $n - 1$ krążków na pręt pomocniczy $z$, potem największy krążek zostaje przeniesiony na pręt docelowy $y$, a na koniec $n - 1$ krążków zostaje przeniesionych z pręta pomocniczego $z$ na pręt docelowy $y$, przy czym pręt startowy $x$ traktowany jest jako pomocniczy.

Algorytm

Specyfikacja

Dane:

• n – liczba całkowita dodatnia,

• x – nazwa pręta startowego,

• y – nazwa pręta docelowego,

• z – nazwa pręta pomocniczego.

Wynik:

ciąg ruchów opisujący rozwiązanie problemu wież z Hanoi z $n$ krążkami, w którym na początku wszystkie krążki znajdują się na pręcie x, a na końcu mają znaleźć się na pręcie y, zaś pomocniczym prętem jest z.

Uwaga: Pojedynczy ruch zapisujemy za pomocą znaku ⇒. Np. C ⇒ B oznacza przeniesienie krążka z pręta C na pręt B.

funkcja wieże(n, x, y, z)
	jeżeli n = 1
		wypisz x ⇒ y
	w przeciwnym razie
 		wieże(n – 1, x, z, y)
		wypisz x ⇒ y
		wieże(n – 1, z, y, x)

Przykład:

Wywołanie wieże(2, A, B, C) spowoduje dwa wywołania rekurencyjne: wieże(1, A, C, B) oraz wieże(1, C, B, A). Ciąg ruchów utworzony przez wieże(2, A, B, C) ma postać:

A ⇒ C, A ⇒ B, C ⇒ B,

gdzie podkreślone ruchy są utworzone przez rekurencyjne wywołania wieże(1, A, C, B) oraz wieże(1, C, B, A).

Zadanie 1.1.

Podaj wszystkie wywołania rekurencyjne funkcji wieże (wraz z ich parametrami), do których dojdzie w wyniku wywołania wieże(3, A, B, C). Odpowiedź zapisz w tabeli, uzupełniając parametry wszystkich wywołań rekurencyjnych.

Rozwiązanie

Zacznijmy od tego, że dla n = 1 nie występują wywołania rekurencyjne. Zostanie natomiast przeniesiony krążek z pręta x na pręt y. Wystąpienie n = 1 oznacza zakończenie serii wywołań. Wynika to z następującego fragmentu kodu:

jeżeli n == 1 wykonaj:
	wypisz x ⇒ y

W przypadku, gdy będziemy mieli więcej niż dwa krążki na pręcie (n > 1), zostanie wykonanych n - 1 przeniesień krążków na pręt pomocniczy, następnie największy krążek zastanie przeniesiony na pręt docelowy, a na niego położone zostanie n - 1 krążków z pręta pomocniczego.

w przeciwnym razie wykonaj:
    wieże(n - 1, x, z, y)
    wypisz x ⇒ y
    wieże(n - 1, z, y, x)

Dla przypomnienia: deklaracja funkcji miała formę: wieże(n, x, y, z) – kluczowa jest tu kolejność: x, y, z.

W rozwiązaniu zadania pomożemy sobie, wykorzystując drzewo wywołań rekurencyjnych. Rozrysujmy jego początek, korzystając z informacji zawartych w tabeli.

R3VDQvnykGeHE

Ilustracja przedstawia schemat. Na górze schematu w prostokątnej ramce jest napis: wieże(3, A, B, C). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(2, A, C, B). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(1, A, B, C).

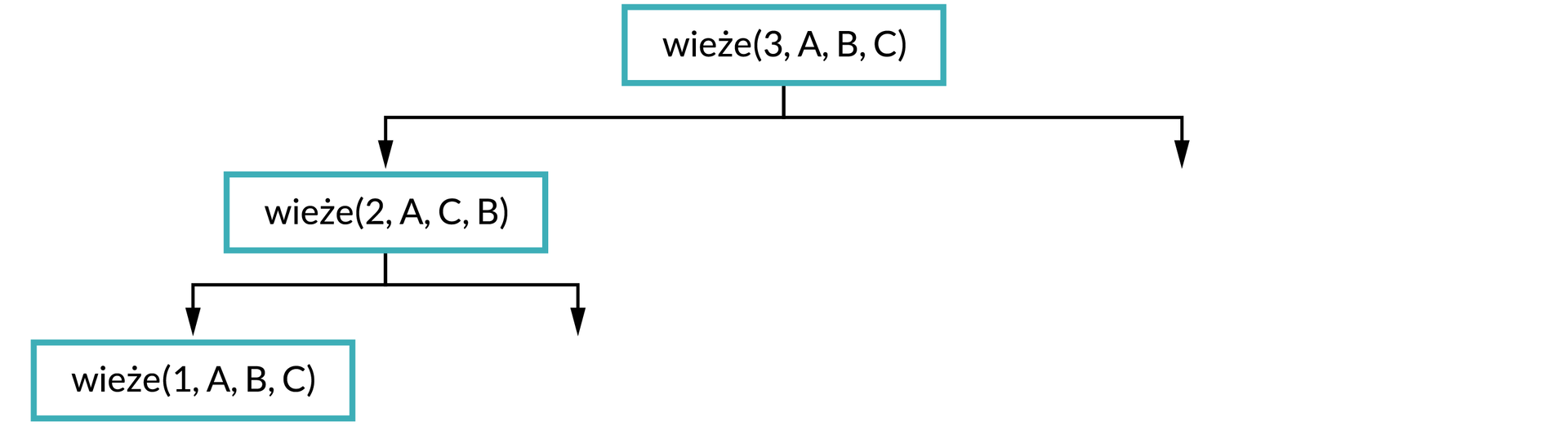
Jakie jest drugie wywołanie rekurencyjne funkcji wieże(2, A, C, B)?

Pamiętaj, że dla wywołania niższego poziomu nadal bierzemy pod uwagę kolejność parametrów z wywołania wyższego poziomu, a więc nadal korzystamy z drugiego wiersza tabeli.

Ponieważ n ≠ 1, przechodzimy do instrukcji w przeciwnym razie.

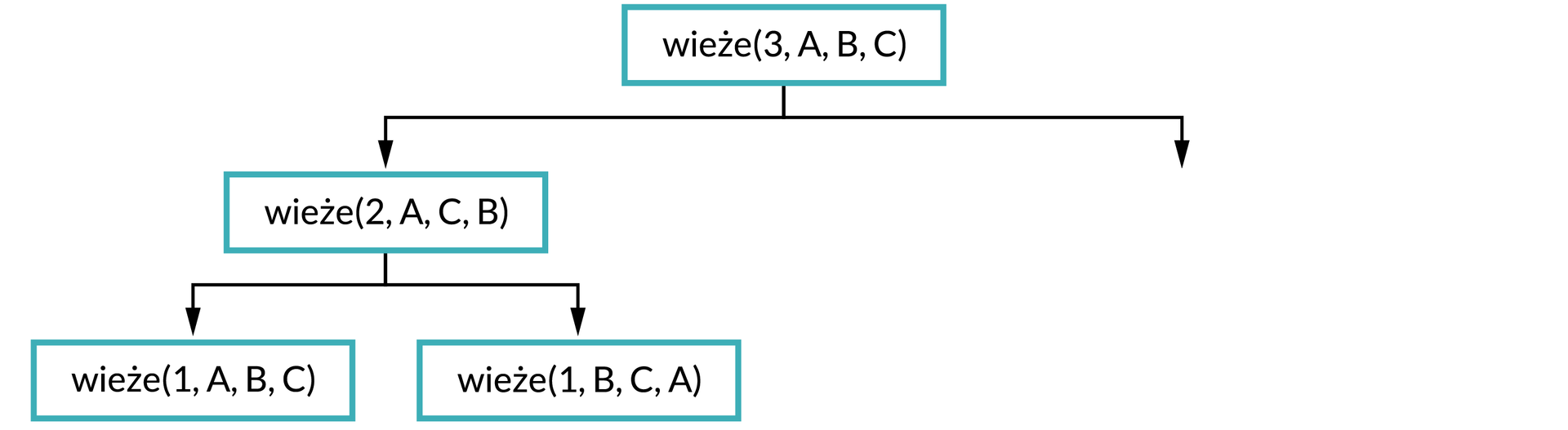
Funkcja wywoła się z parametrem 1. W stosunku do wywołania funkcji wieże(2, A, C, B) pręt docelowy staje się pomocniczym, a pomocniczy – docelowym (linia 5 pseudokodu). Wywoła się zatem funkcja wieże(1, A, B, C). Jest to zgodne z tym, co zapisano w tabeli oraz przedstawiono na drzewie wywołań. Drugie wywołanie rekurencyjne funkcji wieże(2, A, C, B) ma parametr pierwszy parametr również równy 1, natomiast w jego przypadku pręt startowy (A) zostaje prętem pomocniczym, a pomocniczy (B) – startowym.

Możemy zatem dorysować kolejny fragment drzewa wywołań i uzupełnić tabelę.

R1FYAjakRdb0w

Ilustracja przedstawia schemat. Na górze schematu w prostokątnej ramce jest napis: wieże(3, A, B, C). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(2, A, C, B). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(1, A, B, C), pod strzałką po prawej stronie wieże(1, B, C, A).

Analogicznie postępujemy z prawą odnogą drzewa wywołań. Tym razem sprawdzamy drugie rekurencyjne wywołanie funkcji wieże(3, A, B, C) – punktem odniesienia będzie teraz pierwszy wiersz tabeli n = 3.

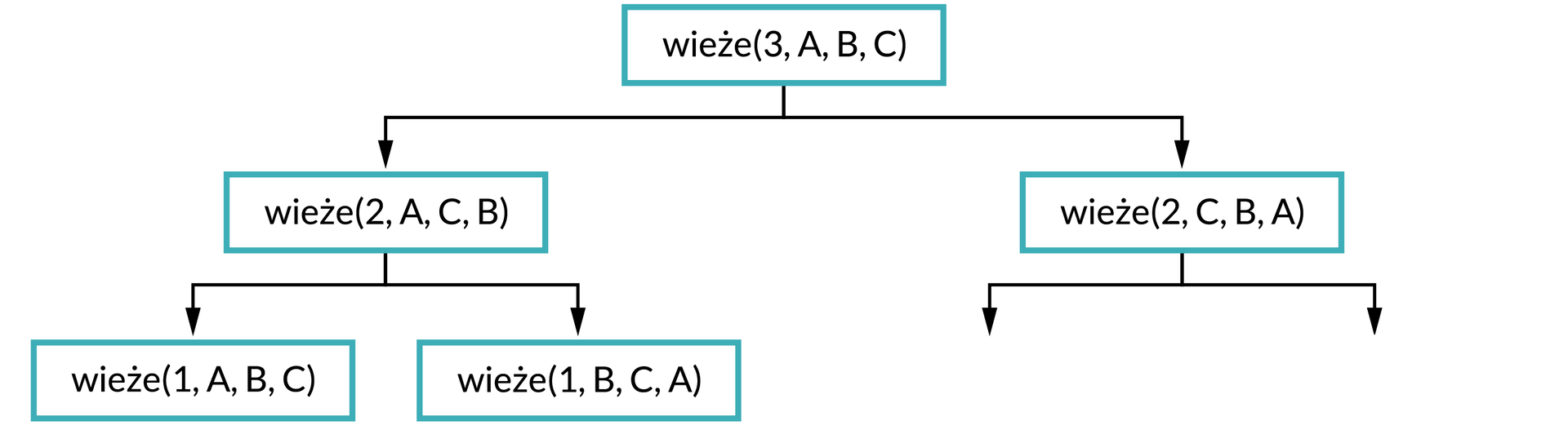
W pierwszym wywołaniu pierwszy parametr przyjmuje wartość 2, pręt startowy nie zmienia się (A), natomiast wcześniejszy pręt pomocniczy zostaje prętem docelowym (C), a docelowy – pomocniczym (B). Zgadza się to z tym, co zapisano w tabeli. Potrzebne jest jeszcze drugie wywołanie rekurencyjne tej funkcji.

Ona również wywoła się z pierwszym parametrem równym 2. Natomiast pręt pomocniczy zostanie prętem startowym (C), pręt docelowy się nie zmieni (B), a pręt startowy zostanie prętem pomocniczym (A). Dorysujmy kolejny fragment drzewa wywołań i uzupełnijmy tabelę.

R1RdL0WImGWal

Ilustracja przedstawia schemat. Na górze schematu w prostokątnej ramce jest napis: wieże(3, A, B, C). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(2, A, C, B). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(1, A, B, C), pod strzałką po prawej stronie wieże(1, B, C, A). Pod strzałką po prawej stronie od pierwszego zapisu napis: wieże(2, C, B, A). Od ramki dwie strzałki w dół.

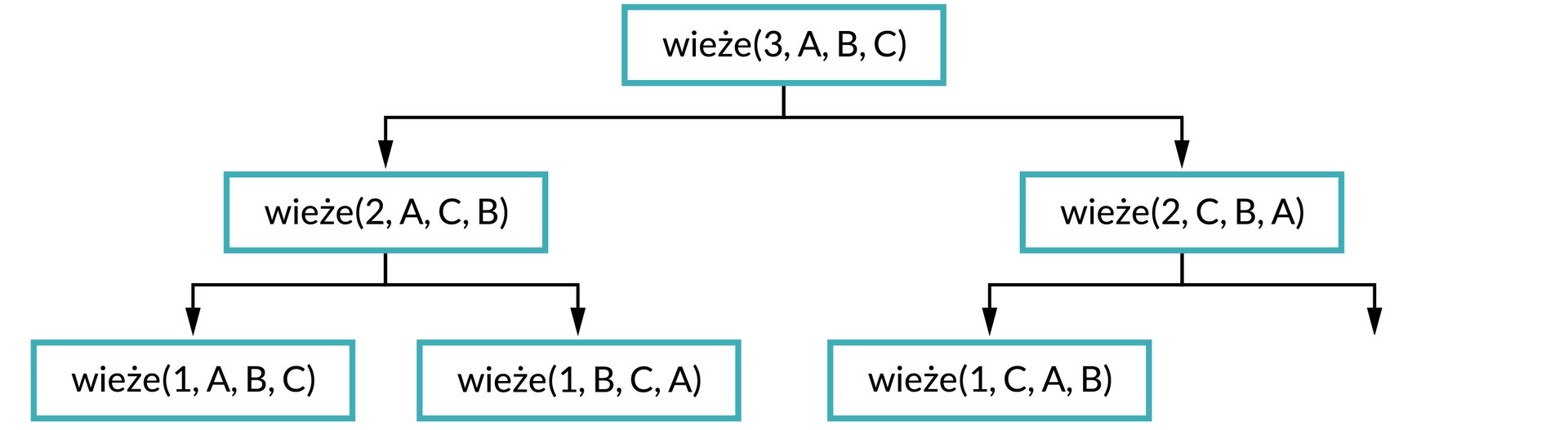
Ostatnim krokiem jest określenie dwóch wywołań rekurencyjnych funkcji wieże(2, C, B, A). Pierwsze z nich wywoła się z pierwszym parametrem równym 1. Pręt startowy się nie zmieni (C), natomiast pręt pomocniczy stanie się prętem docelowym (A), a docelowy – pomocniczym (B). Zapiszmy to w tabeli i uzupełnijmy drzewo wywołań.

RVTAydPccJGG3

Ilustracja przedstawia schemat. Na górze schematu w prostokątnej ramce jest napis: wieże(3, A, B, C). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(2, A, C, B). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(1, A, B, C), pod strzałką po prawej stronie wieże(1, B, C, A). Pod strzałką po prawej stronie od pierwszego zapisu napis: wieże(2, C, B, A). Od ramki dwie strzałki w dół. Pod strzałką po lewej stronie zapis: wieże(1, C, A, B).

Określamy ostanie rekurencyjne wywołanie. Ponownie pierwszym parametrem jest 1. Pręt pomocniczy zostanie prętem startowym (A), nie zmieni się pręt docelowy (B), natomiast pręt startowy zostanie prętem pomocniczym (C).

Uzupełnijmy tabelę i drzewo wywołań rekurencyjnych.

R1NreMb5mDado

Ilustracja przedstawia schemat. Na górze schematu w prostokątnej ramce jest napis: wieże(3, A, B, C). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(2, A, C, B). Od ramki dwie strzałki w dół, pod strzałką po lewej stronie zapis w ramce: wieże(1, A, B, C), pod strzałką po prawej stronie wieże(1, B, C, A). Pod strzałką po prawej stronie od pierwszego zapisu napis: wieże(2, C, B, A). Od ramki dwie strzałki w dół. Pod strzałką po lewej stronie zapis: wieże(1, C, A, B), pod strzałką po prawej stronie zapis: wieże(1, A, B, C).

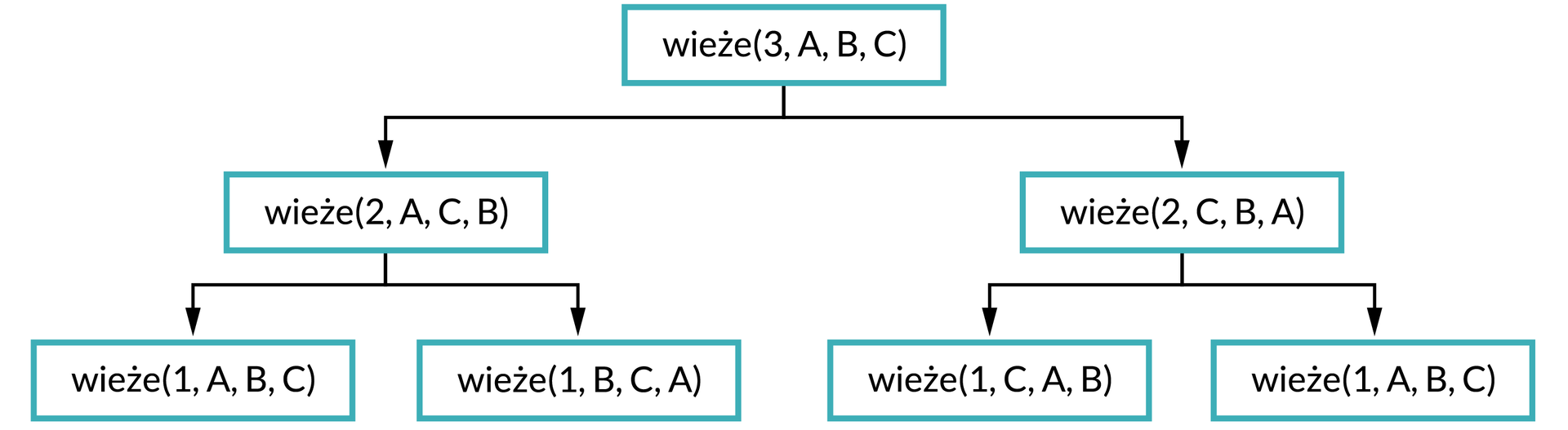
Poprawna odpowiedź

Zadanie 1.2.

Treść polecenia

Prześledź działanie wieże(3, A, B, C) i uzupełnij wygenerowany ciąg ruchów:

A ⇒ B; A ⇒ C; …

Rozwiązanie

W wykonaniu tego zadania pomocna jest tabela z zadania 1.1. Tym razem musimy skupić się na tym, w których momentach w kodzie pojawiają się kolejne instrukcje wypisz. Tabela będzie o tyle pomocna, że będziemy mogli z niej odczytać, jakie było ostatnie wywołanie rekurencyjne, a więc na jakie konkretnie zmienne wskazuje instrukcja wypisz.

Najpierw sprawdźmy jednak, kiedy nasz algorytm wywołuje operację wypisania:

funkcja wieże(n, x, y, z)
	jeżeli n == 1 wykonaj:
    	wypisz x ⇒ y
	w przeciwnym razie wykonaj:
    	wieże(n - 1, x, z, y)
        wypisz x ⇒ y
        wieże(n - 1, z, y, x)

Instrukcja wypisz wywoływana jest w dwóch przypadkach:

1. gdy wywołanie będzie miało parametr n = 1,

2. pomiędzy pierwszym a drugim wywołaniem rekurencyjnym, gdy n > 1.

O ile pierwszy punkt jest dość jasny, o tyle nad drugim trzeba się chwilę zastanowić. Wywołania rekurencyjne charakteryzują się tym, że kod nie przejdzie do następnej linijki, dopóki każde wywołanie rekurencyjne nie zostanie zakończone.

Jeżeli więc doszliśmy do 5. linijki kodu i wywołaliśmy w niej funkcję wieże(n - 1, x, z, y), to nie przejdziemy do następnej linijki tak długo, aż nie zostaną sfinalizowane wszystkie „rozgałęzienia”, związane z wywoływaniem kolejnych wywołań rekurencyjnych niższego stopnia. Dopiero gdy każda z tych „ścieżek” znajdzie swój koniec w postaci funkcji wieże z parametrem n = 1, dokonamy operacji wypisania.

Skoro wiemy już dokładnie, kiedy wystąpią operacje wypisania, spróbujmy dokonać symulacji działania algorytmu. Każde kolejne wywołanie rekurencyjne będzie zasygnalizowane wcięciem.

Każda operacja wypisania będzie przy okazji opatrzona numerem [1] bądź [2] w zależności od tego, z którym warunkiem związane jest to wypisanie. Dla przypomnienia: 1 jest zarezerwowana dla wariantu, gdy n = 1, zaś 2 – gdy n > 1.

wieże(3, a, b, c)
	wieże(2, a, c, b)
    	wieże(1, a, b, c)
        	A ⇒ B [1]
        A ⇒ C [2]
        wieże(1, b, c, a)
        	B ⇒ C [1]
	A ⇒ B [2]
    wieże(2, c, b, a)
    	wieże(1, c, a, b)
        	C ⇒ A [1]
        C ⇒ B [2]
        wieże(1, a, b, c)
        	A ⇒ B [1]

Poprawna odpowiedź

A ⇒ B; A ⇒ C; B ⇒ C; A ⇒ B; C ⇒ A; C ⇒ B; A ⇒ B.

Słownik